No CrossRef data available.
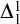 $\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
$\Delta ^{1}_{1}$ DETERMINACY AND ℵω1Published online by Cambridge University Press: 07 January 2021
We consider a seemingly weaker form of 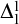 $\Delta ^{1}_{1}$
Turing determinacy.
$\Delta ^{1}_{1}$
Turing determinacy.
Let 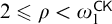 $2 \leqslant \rho < \omega _{1}^{\mathsf {CK}}$
,
$2 \leqslant \rho < \omega _{1}^{\mathsf {CK}}$
, 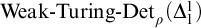 $\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
is the statement:
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
is the statement:
Every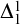 $\Delta ^{1}_{1}$
set of reals cofinal in the Turing degrees contains two Turing distinct,
$\Delta ^{1}_{1}$
set of reals cofinal in the Turing degrees contains two Turing distinct, 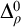 $\Delta ^{0}_{\rho }$
-equivalent reals.
$\Delta ^{0}_{\rho }$
-equivalent reals.
We show in 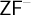 $\mathsf {ZF}^-$
:
$\mathsf {ZF}^-$
:
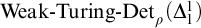 $\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
implies: for every
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
implies: for every 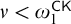 $\nu < \omega _{1}^{\mathsf {CK}}$
there is a transitive model
$\nu < \omega _{1}^{\mathsf {CK}}$
there is a transitive model 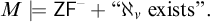 ${M \models \mathsf {ZF}^{-} + \textrm{``}\aleph _{\nu } \textrm{ exists''.}}$
${M \models \mathsf {ZF}^{-} + \textrm{``}\aleph _{\nu } \textrm{ exists''.}}$
As a corollary:
If every cofinal 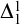 $\Delta ^{1}_{1}$
set of Turing degrees contains both a degree and its jump, then for every
$\Delta ^{1}_{1}$
set of Turing degrees contains both a degree and its jump, then for every 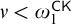 $\nu < \omega_1^{\mathsf{CK}}$
, there is atransitive model:
$\nu < \omega_1^{\mathsf{CK}}$
, there is atransitive model: 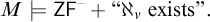 $M \models \mathsf{ZF}^{-} + \textrm{``}\aleph_\nu \textrm{ exists''.}$
$M \models \mathsf{ZF}^{-} + \textrm{``}\aleph_\nu \textrm{ exists''.}$
• With a simple proof, this improves upon a well-known result of Harvey Friedman on the strength of Borel determinacy (though not assessed level-by-level).
• Invoking Tony Martin’s proof of Borel determinacy, 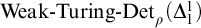 $\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
implies
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
implies 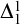 $\Delta ^{1}_{1}$
determinacy.
$\Delta ^{1}_{1}$
determinacy.
• We show further that, assuming 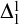 $\Delta ^{1}_{1}$
Turing determinacy, or Borel Turing determinacy, as needed:
$\Delta ^{1}_{1}$
Turing determinacy, or Borel Turing determinacy, as needed:
– Every cofinal 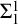 $\Sigma ^{1}_{1}$
set of Turing degrees contains a “hyp-Turing cone”:
$\Sigma ^{1}_{1}$
set of Turing degrees contains a “hyp-Turing cone”: 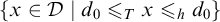 ${\{x \in \mathcal {D} \mid d_{0} \leqslant _{T} x \leqslant _{h} d_{0} \}}$
.
${\{x \in \mathcal {D} \mid d_{0} \leqslant _{T} x \leqslant _{h} d_{0} \}}$
.
– For a sequence 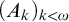 $(A_{k})_{k < \omega }$
of analytic sets of Turing degrees, cofinal in
$(A_{k})_{k < \omega }$
of analytic sets of Turing degrees, cofinal in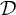 $\mathcal {D}$
,
$\mathcal {D}$
, 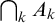 $\bigcap _{k} A_{k}$
is cofinal in
$\bigcap _{k} A_{k}$
is cofinal in 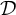 $\mathcal {D}$
.
$\mathcal {D}$
.
Presented at the 12th Panhellenic Logic Symposium—Crete, June 2019.