Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-28T02:43:35.333Z Has data issue: false hasContentIssue false
  • English
  • Français

THE UNDECIDABILITY OF THE DEFINABILITY OF PRINCIPAL SUBCONGRUENCES

Published online by Cambridge University Press:  22 April 2015

MATTHEW MOORE
MATTHEW MOORE*
Affiliation:
VANDERBILT UNIVERSITY NASHVILLE, TN 37240, USAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

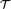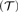For each Turing machine ${\cal T}$, we construct an algebra $\mathbb{A}$′$\left( {\cal T} \right)$ such that the variety generated by $\mathbb{A}$′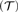$\left( {\cal T} \right)$ has definable principal subcongruences if and only if 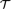${\cal T}$ halts, thus proving that the property of having definable principal subcongruences is undecidable for a finite algebra. A consequence of this is that there is no algorithm that takes as input a finite algebra and decides whether that algebra is finitely based.

Keywords

definable principal subcongruencesundecidablefinite basisfinite residual bound
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 2 , June 2015 , pp. 384 - 432
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Baker, Kirby A., Finite equational bases for finite algebras in a congruence-distributive equational class. Advances in Mathematics, vol. 24 (1977), no. 3, pp. 207–243.Google Scholar
Baker, Kirby A. and Wang, Ju, Definable principal subcongruences. Algebra Universalis, vol. 47 (2002), no. 2, pp. 145–151.Google Scholar
Fried, E., Grätzer, G., and Quackenbush, R., Uniform congruence schemes. Algebra Universalis, vol. 10 (1980), no. 2, pp. 176–188.Google Scholar
Hobby, David and McKenzie, Ralph, The structure of finite algebras, Contemporary Mathematics, vol. 76, American Mathematical Society, Providence, RI, 1988.Google Scholar
McKenzie, Ralph, Para primal varieties: A study of finite axiomatizability and definable principal congruences in locally finite varieties. Algebra Universalis, vol. 8 (1978), no. 3, pp. 336–348.CrossRefGoogle Scholar
McKenzie, Ralph, The residual bound of a finite algebra is not computable. International Journal of Algebra and Computation, vol. 6 (1996), no. 1, pp. 29–48.Google Scholar
McKenzie, Ralph, The residual bounds of finite algebras. International Journal of Algebra and Computation, vol. 6 (1996), no. 1, pp. 1–28.Google Scholar
McKenzie, Ralph, Tarski’s finite basis problem is undecidable. International Journal of Algebra and Computation, vol. 6 (1996), no. 1, 49–104.Google Scholar
Moore, Matthew, The variety generated by $\mathbb{A}$$\left( {\cal T} \right)$ – two counterexamples, available athttp://arxiv.org/abs/1304.4659.Google Scholar
Willard, Ross, Tarski’s finite basis problem via $A\left( {\cal T} \right)$, Transactions of the American Mathematical Society, vol. 349 (1997), no. 7, pp. 2755–2774.CrossRefGoogle Scholar
Willard, Ross, A finite basis theorem for residually finite, congruence meet-semidistributive varieties, this Journal, vol. 65 (2000), no. 1, pp. 187–200.Google Scholar