Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-28T09:46:51.493Z Has data issue: false hasContentIssue false
  • English
  • Français

THE REVERSE MATHEMATICS OF ${\mathsf {CAC\ FOR\ TREES}}$

Part of: General logic Computability and recursion theory

Published online by Cambridge University Press:  28 April 2023

JULIEN CERVELLE ,
WILLIAM GAUDELIER  and
LUDOVIC PATEY Open the ORCID record for LUDOVIC PATEY [Opens in a new window]
JULIEN CERVELLE
Affiliation:
LABORATOIRE DALGORITHMIQUE, COMPLEXITÉ ET LOGIQUE UNIVERSITÉ PARIS-EST CRÉTEIL F-94010 CRETEIL, FRANCE E-mail: [email protected] E-mail: [email protected] URL: https://jc.lacl.fr
WILLIAM GAUDELIER
Affiliation:
LABORATOIRE DALGORITHMIQUE, COMPLEXITÉ ET LOGIQUE UNIVERSITÉ PARIS-EST CRÉTEIL F-94010 CRETEIL, FRANCE E-mail: [email protected] E-mail: [email protected] URL: https://jc.lacl.fr
LUDOVIC PATEY*
Affiliation:
IMJ-PRG, CNRS, ÉQUIPE DE LOGIQUE UNIVERSITÉ DE PARIS PARIS, FRANCE URL: http://ludovicpatey.com
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

${\mathsf {CAC\ for\ trees}}$ is the statement asserting that any infinite subtree of 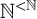$\mathbb {N}^{<\mathbb {N}}$ has an infinite path or an infinite antichain. In this paper, we study the computational strength of this theorem from a reverse mathematical viewpoint. We prove that ${\mathsf {CAC\ for\ trees}}$ is robust, that is, there exist several characterizations, some of which already appear in the literature, namely, the statement $\mathsf {SHER}$ introduced by Dorais et al. [8], and the statement 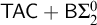$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$ where $\mathsf {TAC}$ is the tree antichain theorem introduced by Conidis [6]. We show that ${\mathsf {CAC\ for\ trees}}$ is computationally very weak, in that it admits probabilistic solutions.

Keywords

chain antichainRamseyreverse mathematics

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics)
Secondary: 03D80: Applications of computability and recursion theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 3 , September 2024 , pp. 1189 - 1211
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Astor, E. P., Bienvenu, L., Dzhafarov, D., Patey, L., Shafer, P., Solomon, R., and Westrick, L. B., The weakness of typicality, in preparation.Google Scholar
Belanger, D., Chong, C., Li, W., Wang, W., and Yang, Y., Where pigeonhole principles meet König lemmas , Transactions of the American Mathematical Society, vol. 374 (2021), pp. 8275–8303.Google Scholar
Binns, S., Kjos-Hanssen, B., Lerman, M., Schmerl, J. H., and Solomon, R., Self-embeddings of computable trees. Notre Dame Journal of Formal Logic, vol. 49 (2008), no. 1, pp. 1–37.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
Chong, C., Lempp, S., and Yang, Y., On the role of the collection principle for ${\varSigma}_2^0$ -formulas in second-order reverse mathematics . Proceedings of the American Mathematical Society, vol. 138 (2010), no. 3, pp. 1093–1100.CrossRefGoogle Scholar
Conidis, C. J., Computability and combinatorial aspects of minimal prime ideals in Noetherian rings, submitted.Google Scholar
Dorais, F. G., On a theorem of Hajnal and Surányi, 2012.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems . Transactions of the American Mathematical Society, vol. 368 (2016), no. 2, pp. 1321–1359.CrossRefGoogle Scholar
Dzhafarov, D. D., Hirschfeldt, D. R., and Reitzes, S. C., Reduction games, provability, and compactness . Journal of Mathematical Logic, vol. 22 (2022), p. 2250009.CrossRefGoogle Scholar
Flood, S., Reverse mathematics and a Ramsey-type König’s lemma, this Journal, vol. 77 (2012), no. 4, pp. 1272–1280.Google Scholar
Herrmann, E., Infinite chains and antichains in computable partial orderings, this Journal, vol. 66 (2001), no. 2, pp. 923–934.Google Scholar
Hirschfeldt, D. R., Slicing the Truth: On the computable and reverse mathematics of combinatorial principles, Lecture Notes Series. Institute for Mathematical Sciences. National University of Singapore, vol. 28, World Scientific, Hackensack, NJ, 2015, Edited and with a foreword by Chitat Chong, Qi Feng, Theodore A. Slaman, W. Hugh Woodin and Yue Yang.Google Scholar
Hirschfeldt, D. R. and Shore, R. A., Combinatorial principles weaker than Ramsey’s theorem for pairs, this Journal, vol. 72 (2007), no. 1, pp. 171–206.Google Scholar
Hirschfeldt, D. R., Shore, R. A., and Slaman, T. A., The atomic model theorem and type omitting . Transactions of the American Mathematical Society, vol. 361 (2009), no. 11, pp. 5805–5837.CrossRefGoogle Scholar
Jockusch, C. G. and Soare, R. I.,  ${\pi}_1^0$ classes and degrees of theories . Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
Lerman, M., Solomon, R., and Towsner, H., Separating principles below Ramsey’s theorem for pairs . Journal of Mathematical Logic, vol. 13 (2013), no. 2, p. 1350007.CrossRefGoogle Scholar
Patey, L., Ramsey-like theorems and moduli of computation, this Journal, vol. 87 (2022), 72–108.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar