Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-28T08:24:59.826Z Has data issue: false hasContentIssue false
  • English
  • Français

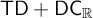NOTE ON $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING 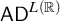$\mathsf {AD}^{L(\mathbb {R})}$

Part of: Set theory

Published online by Cambridge University Press:  04 January 2024

SEAN CODY
SEAN CODY*
Affiliation:
DEPARTMENT OF MATHEMATICS UC BERKELEY BERKELEY, CA 94720, USA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A short core model induction proof of 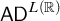$\mathsf {AD}^{L(\mathbb {R})}$ from 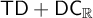$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$.

Keywords

inner model theorycore model inductiondeterminacy

MSC classification

Primary: 03E45: Inner models, including constructibility, ordinal definability, and core models 03E60: Determinacy principles
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 1 , March 2024 , pp. 211 - 217
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Hugh Woodin, W., Turing determinacy and Suslin sets . New Zealand Journal of Mathematics, vol. 52 (2022), pp. 845–863.CrossRefGoogle Scholar
Kechris, A. S. and Hugh Woodin, W., Equivalence of partition properties and determinacy . Proceedings of the National Academy of Sciences, vol. 80 (1983), no. 6, pp. 1783–1786.CrossRefGoogle ScholarPubMed
Kechris, A. S. and Solovay, R. M., On the relative consistency strength of determinacy hypothesis . Transactions of the American Mathematical Society, vol. 290 (1985), no. 1, pp. 179–211.Google Scholar
Martin, D. A., The axiom of determinateness and reduction principles in the analytical hierarchy . Bulletin of the American Mathematical Society, vol. 74 (1968), no. 4, pp. 687–689.CrossRefGoogle Scholar
Neeman, I., Optimal proofs of determinacy II . Journal of Mathematical Logic, vol. 2 (2002), no. 2, pp. 227–258.CrossRefGoogle Scholar
Peng, Y. and Yu, L., TD implies CCR . Advances in Mathematics, vol. 384 (2021), p. 107755.CrossRefGoogle Scholar
Schindler, R. and Steel, J., The core model induction. Available at https://ivv5hpp.uni-muenster.de/u/rds/.Google Scholar
Steel, J. and Zoble, S., Determinacy from strong reflection . Transactions of the American Mathematical Society, vol. 366 (2014), no. 8, pp. 4443–4490.CrossRefGoogle Scholar
Steel, J. R., The Core Model Iterability Problem, Lecture Notes in Logic, Cambridge University Press, Cambridge, 2017.CrossRefGoogle Scholar
Steel, J. R. and Hugh Woodin, W., HOD as a core model , Ordinal Definability and Recursion Theory: The Cabal Seminar, vol. 3, Lecture Notes in Logic, Cambridge University Press, Cambridge, 2016, pp. 257–346.CrossRefGoogle Scholar
Wilson, T., Contributions to descriptive inner model theory, Ph.D. thesis, University of California, Berkeley, 2012.Google Scholar