No CrossRef data available.
Published online by Cambridge University Press: 10 June 2021
We study the Rudin–Keisler pre-order on Fréchet–Urysohn ideals on 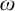 $\omega $
. We solve three open questions posed by S. García-Ferreira and J. E. Rivera-Gómez in the articles [5] and [6] by establishing the following results:
$\omega $
. We solve three open questions posed by S. García-Ferreira and J. E. Rivera-Gómez in the articles [5] and [6] by establishing the following results:
• For every AD family 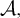 $\mathcal {A},$
there is an AD family
$\mathcal {A},$
there is an AD family 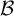 $\mathcal {B}$
such that
$\mathcal {B}$
such that 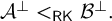 $\mathcal {A}^{\perp } <_{{\textsf {RK}}}\mathcal {B}^{\perp }.$
$\mathcal {A}^{\perp } <_{{\textsf {RK}}}\mathcal {B}^{\perp }.$
• If 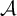 $\mathcal {A}$
is a nowhere MAD family of size
$\mathcal {A}$
is a nowhere MAD family of size 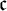 $\mathfrak {c}$
then there is a nowhere MAD family
$\mathfrak {c}$
then there is a nowhere MAD family 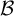 $\mathcal {B}$
such that
$\mathcal {B}$
such that 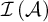 $\mathcal {I}\left (\mathcal {A}\right ) $
and
$\mathcal {I}\left (\mathcal {A}\right ) $
and 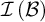 $\mathcal {I}\left ( \mathcal {B}\right ) $
are Rudin–Keisler incomparable.
$\mathcal {I}\left ( \mathcal {B}\right ) $
are Rudin–Keisler incomparable.
• There is a family 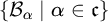 $\left \{ \mathcal {B}_{\alpha }\mid \alpha \in \mathfrak {c}\right \} $
of nowhere MAD families such that if
$\left \{ \mathcal {B}_{\alpha }\mid \alpha \in \mathfrak {c}\right \} $
of nowhere MAD families such that if 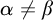 $\alpha \neq \beta $
, then
$\alpha \neq \beta $
, then 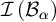 $\mathcal {I}\left ( \mathcal {B}_{\alpha }\right ) $
and
$\mathcal {I}\left ( \mathcal {B}_{\alpha }\right ) $
and 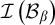 $\mathcal {I}\left ( \mathcal {B}_{\beta }\right ) $
are Rudin–Keisler incomparable.
$\mathcal {I}\left ( \mathcal {B}_{\beta }\right ) $
are Rudin–Keisler incomparable.
Here 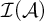 $\mathcal {I}(\mathcal {A})$
denotes the ideal generated by an AD family
$\mathcal {I}(\mathcal {A})$
denotes the ideal generated by an AD family  $\mathcal {A}$
.
$\mathcal {A}$
.
In the context of hyperspaces with the Vietoris topology, for a Fréchet–Urysohn-filter 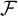 $\mathcal {F}$
we let
$\mathcal {F}$
we let  $\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
be the hyperspace of nontrivial convergent sequences of the space consisting of
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F}\right ) \right ) $
be the hyperspace of nontrivial convergent sequences of the space consisting of 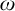 $\omega $
as discrete subset and only one accumulation point
$\omega $
as discrete subset and only one accumulation point 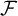 $\mathcal {F}$
whose neighborhoods are the elements of
$\mathcal {F}$
whose neighborhoods are the elements of 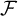 $\mathcal {F}$
together with the singleton
$\mathcal {F}$
together with the singleton 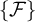 $\{\mathcal {F}\}$
. For a FU-filter
$\{\mathcal {F}\}$
. For a FU-filter 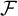 $\mathcal {F}$
we show that the following are equivalent:
$\mathcal {F}$
we show that the following are equivalent:
• 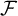 $\mathcal {F}$
is a FUF-filter.
$\mathcal {F}$
is a FUF-filter.
• 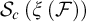 $\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F} \right ) \right ) $
is Baire.
$\mathcal {S}_{c}\left ( \mathcal {\xi }\left ( \mathcal {F} \right ) \right ) $
is Baire.