Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-28T15:50:22.916Z Has data issue: false hasContentIssue false
  • English
  • Français

A shear and elongational decomposition approach of the rate-of-deformation tensor for non-Newtonian flows with mixed kinematics

Published online by Cambridge University Press:  10 December 2024

Paulo J. Oliveira Open the ORCID record for Paulo J. Oliveira [Opens in a new window]
Paulo J. Oliveira*
Affiliation:
Departamento de Engenharia Electromecânica, C-MAST, Universidade da Beira Interior, 6201-001 Covilhã, Portugal
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

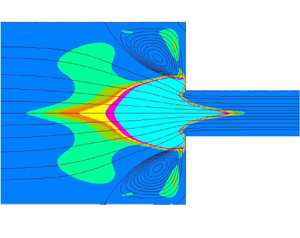
We propose a novel approach for non-Newtonian viscoelastic steady flows based on a decomposition of the rate-of-deformation tensor which here, in a simplified version, leads to an anisotropic generalised Newtonian fluid-like model with separated treatment of kinematics pertaining to shear and extensional flows. Care is taken to assure that the approach is objective and does not introduce spurious effects due to dependence on a specific reference frame. This is done by separating the rate-of-deformation tensor into shear and elongational components, with the local scalar shear and elongation rates being the second invariant of each tensor separately, and by modifying the method used to separate the rate-of-deformation tensor so that it becomes independent of superimposed rigid rotations, thus satisfying the principle of material indifference. We assess the model with two test cases: planar contraction flow, often employed to evaluate numerical methods or constitutive equations and for which experimentally observed corner vortex enhancement and pressure drop increase are seldom found in numerical simulations; and flow past confined or unconfined cylinders, for which experiments indicate a drag increase due to elasticity and most predictions give a drag decrease. With our anisotropic model, incorporating additional elongational-flow-related terms, large vortices and accentuated pressure drop coefficients can be predicted for the contraction problem and enhanced drag coefficient for the cylinder problems. This is the first work where problems of non-Newtonian fluid mechanics are solved numerically with separation of strain rate into shear and elongational components.

JFM classification

Non-Newtonian Flows: Viscoelasticity Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A17
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alam, M.I., Raj, A., Khan, P.M., Kumar, S. & Roy, S. 2021 Numerical simulation of flow of a shear-thinning Carreau fluid over a transversely oscillating cylinder. J. Fluid Mech. 921, A23.CrossRefGoogle Scholar
Alves, M.A., Oliveira, P.J. & Pinho, F.T. 2003 Benchmark solutions for the flow of Oldroyd-B and PTT fluids in planar contractions. J. Non-Newtonian Fluid Mech. 110, 45–75.CrossRefGoogle Scholar
Alves, M.A., Oliveira, P.J. & Pinho, F.T. 2004 On the effect of contraction ratio in viscoelastic flow through abrupt contractions. J. Non-Newtonian Fluid Mech. 122, 117–130.CrossRefGoogle Scholar
Alves, M.A., Oliveira, P.J. & Pinho, F.T. 2021 Numerical methods for viscoelastic fluid flows. Annu. Rev. Fluid Mech. 53, 509-541.CrossRefGoogle Scholar
Alves, M.A., Pinho, F.T. & Oliveira, P.J. 2001 The flow of viscoelastic fluids past a cylinder: finite-volume high-resolution methods. J. Non-Newtonian Fluid Mech. 97, 207–232.CrossRefGoogle Scholar
Batchelor, G.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Binding, D.M. & Walters, K. 1988 On the use of flow through a contraction in estimating the extensional viscosity of mobile polymer solutions. J. Non-Newtonian Fluid Mech. 30, 233–250.CrossRefGoogle Scholar
Bird, R.B., Armstrong, R.C., Hassager, O. 1987 Dynamics of Polymeric Liquids, Volume I: Fluid Mechanics, 2nd edn. Wiley.Google Scholar
Boyko, E. & Stone, H.A. 2021 Flow rate – pressure drop relations for shear-thinning fluids in narrow channels: approximate solutions and comparison with experiments. J. Fluid Mech. 923, R5.CrossRefGoogle Scholar
Boyko, E. & Stone, H.A. 2022 Pressure driven flow of the viscoelastic Oldroyd-B fluid in narrow geometries: analytical results and comparison with simulations. J. Fluid Mech. 936, A23.CrossRefGoogle Scholar
Chilcott, M.D. & Rallison, J.M. 1988 Creeping flow of dilute polymer solutions past cylinders and spheres. J. Non-Newtonian Fluid Mech. 29, 381–432.CrossRefGoogle Scholar
Coleman, B.D. & Noll, W. 1961 Foundations of linear viscoelasticity. Rev. Mod. Phy. 33, 239–249.CrossRefGoogle Scholar
Coleman, B.D. & Noll, W. 1962 Steady extension of incompressible simple fluids. Phy Fluids 5, 840–843.CrossRefGoogle Scholar
Criminale, W.O., Ericksen, J.L. & Filbey, G.L. 1958 Steady shear flow of non-Newtonian fluids, Arch. Rat. Mech. Anal. 1, 410-417.CrossRefGoogle Scholar
Debbaut, B. & Crochet, M.J. 1988 Extensional effects in complex flows. J. Non-Newtonian Fluid Mech. 30, 169–184.CrossRefGoogle Scholar
Evans, R.E. & Walters, K. 1986 Flow characteristics associated with abrupt changes in geometry in the case of highly elastic liquids. J. Non-Newt. Fluid Mech. 20, 11-29.CrossRefGoogle Scholar
Haller, G. 2021 Can vortex criteria be objectivized? J. Fluid Mech. 908, A25.CrossRefGoogle Scholar
Haward, S.J., Varchanis, S., McKinley, G.H., Alves, M.A. & Shen, A.Q. 2023, Extensional rheometry of mobile fluids. Part II. Comparison between the uniaxial, planar, and biaxial extensional rheology of dilute polymer solutions using numerically optimized stagnation point microfluidic devices. J. Rheol. 67(5), 1011-1030.CrossRefGoogle Scholar
Hodgkinson, R., Chaffin, C.T., Zimmerman, W.B.J., Holland, C. & Howse, J.R. 2022, Extensional flow affecting shear viscosity: experimental evidence and comparison with models. J. Rheol. 66(4), 793-809.CrossRefGoogle Scholar
Huang, P.Y., & Feng, J. 1995 Wall effects on the flow of viscoelastic fluids around a circular cylinder. J. Non-Newtonian Fluid Mech. 60, 179–198.CrossRefGoogle Scholar
James, D.F. & Acosta, A.J. 1970 The laminar flow of dilute polymer solutions around circular cylinders. J. Fluid Mech. 42, 269–288.CrossRefGoogle Scholar
Jones, D.M., Walters, K. & Williams, P.R. 1987 On the extensional viscosity of mobile polymer solutions. Rheol. Acta 26, 20–30.CrossRefGoogle Scholar
Kim, S.G. & Lee, H.S. 2019 Concentration dependence of the extensional relaxation time and finite extensibility in dilute and semidilute polymer solutions using a microfluidic rheometer. Macromolecules 52, 9585–9593.CrossRefGoogle Scholar
Kolar, V. 2007 Vortex identification: new requirements and limitations. Intl J. Heat Fluid Flow 28, 638-652.CrossRefGoogle Scholar
Koppol, A.P., Sureshkumar, R., Abedijaberi, A. & Khomami, B. 2009 Anomalous pressure drop behaviour of mixed kinematics flows of viscoelastic polymer solutions: a multiscale simulation approach. J. Fluid Mech. 631, 231–253.CrossRefGoogle Scholar
Kronborg, J. & Hoffman, J. 2023 The triple decomposition of the velocity gradient tensor as a standardized real Schur form. Phys. Fluids 35, 031703.CrossRefGoogle Scholar
Larson, R.G. 1988 Constitutive Equations for Polymer Melts and Solutions. Butterworths.Google Scholar
Larson, R.G., Shaqfeh, E.S.G. & Muller, S.J. 1990 A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 218, 573-600.CrossRefGoogle Scholar
Leigh, D.C. 1968 Nonlinear Continuum Mechanics. McGraw-Hill.Google Scholar
López-Aguilar, J.E., Tamaddon-Jahromi, H.R., Webster, M.F. & Walters, K. 2016 Numerical vs experimental pressure drops for Boger fluids in sharp-corner contraction flows. Phys. Fluids 28, 103104.CrossRefGoogle Scholar
Manero, O. & Mena, B. 1981 On the slow flow of viscoelastic liquids past a circular cylinder. J. Non-Newtonian Fluid Mech. 9, 379–387.CrossRefGoogle Scholar
McKinley, G.H., Armstrong, R.C. & Brown, R.A. 1993 The wake instability in viscoelastic flow past confined circular cylinders. Phil. Trans. R. Soc. Lond. A 344, 265–304.Google Scholar
McKinley, G.H. & Sridhar, T. 2002 Filament-stretching rheometry of complex fluids. Annu. Rev. Fluid Mech. 34, 375-415.CrossRefGoogle Scholar
Moffatt, H.K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1-18.CrossRefGoogle Scholar
Nigen, S. & Walters, K. 2002 Viscoelastic contraction flows: comparison of axisymmetric and planar configurations. J. Non-Newtonian Fluid Mech. 102, 343–359.CrossRefGoogle Scholar
Oldroyd, J.G. 1950 On the formulation of rheological equations of state. Proc. R. Soc. A 200, 523-541.Google Scholar
Oliveira, M.S.N., Oliveira, P.J., Pinho, F.T. & Alves, M.A. 2007 Effect of contraction ratio upon viscoelastic flow in contractions: the axisymmetric case. J. Non-Newtonian Fluid Mech. 147, 92–108.CrossRefGoogle Scholar
Oliveira, P.J. & Miranda, A.I.P. 2005 A numerical study of steady and unsteady viscoelastic flow past bounded cylinders. J. Non-Newtonian Fluid Mech. 127, 51–66.CrossRefGoogle Scholar
Oliveira, P.J., Pinho, F.T. & Pinto, G.A. 1998 Numerical simulation of non-linear elastic flows with a general collocated finite-volume method. J. Non-Newtonian Fluid Mech. 79, 1–43.CrossRefGoogle Scholar
Pakdel, P. & McKinley, G.H. 1996 Elastic instability and curved streamlines, Phys. Rev. Lett. 77 (12), 2459–2462.CrossRefGoogle ScholarPubMed
Petrie, C.J.S. 2006 Extensional viscosity: a critical discussion. J. Non-Newtonian Fluid Mech. 137, 15–23.CrossRefGoogle Scholar
Poole, R.J. 2023 Inelastic and flow-type parameter models for non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 320, 105106.CrossRefGoogle Scholar
Poole, R.J. 2024 On the use of the Astarita flow field for viscoelastic fluids to develop a generalised Newtonian fluid model incorporating flow type (GNFFTy). J. Fluid Mech. 987, A2.CrossRefGoogle Scholar
Reiner, M. 1945 A mathematical theory of dilatancy. Am. J. Maths 67, 350–362.CrossRefGoogle Scholar
Ribeiro, V.M., Coelho, P.M., Pinho, F.T. & Alves, M.A. 2014 Viscoelastic fluid flow past a confined cylinder: three-dimensional effects and stability. Chem. Engng Sci. 111 (2014) 364-380.CrossRefGoogle Scholar
Rivlin, R.S. 1948 The hydrodynamics of non-Newtonian fluids I. Proc. R. Soc. Lond. A 193, 260–281.Google Scholar
Rodd, L.E., Cooper-White, J.J., Boger, D.V. & McKinley, G.H. 2007 Role of the elasticity number in the entry flow of dilute polymer solutions in micro-fabricated contraction geometries. J. Non-Newtonian Fluid Mech. 143, 170–191.CrossRefGoogle Scholar
Rodd, L.E., Scott, T.P., Boger, D.V., Cooper-White, J.J. & McKinley, G.H. 2005 The inertio-elastic planar entry flow of low-viscosity elastic fluids in micro-fabricated geometries. J. Non-Newtonian Fluid Mech. 129, 1–22.CrossRefGoogle Scholar
Rothstein, J.P. & McKinley, G.H. 1999 Extensional flow of a polystyrene Boger fluid through a 4:1:4 axisymmetric contraction/expansion. J. Non-Newtonian Fluid Mech. 86, 61–88.CrossRefGoogle Scholar
Rothstein, J.P. & McKinley, G.H. 2001 The axisymmetric contraction – expansion: the role of extensional rheology on vortex growth dynamics and the enhanced pressure drop, J. Non-Newtonian Fluid Mech. 98, 33–63.CrossRefGoogle Scholar
Solomon, M.J. & Muller, S.J. 1996 Flow past a sphere in polystyrene-based Boger fluids: the effect on the drag coefficient of finite extensibility, solvent quality and polymer molecular weight. J. Non-Newtonian Fluid Mech. 62, 81–94.CrossRefGoogle Scholar
Talwar, K.K., & Khomami, B. 1995 Flow of viscoelastic fluids past periodic square arrays of cylinders: inertial and shear-thinning viscosity and elasticity effects. J. Non-Newtonian Fluid Mech. 57, 177–202.CrossRefGoogle Scholar
Tanner, R.I. 1988 Engineering Rheology, rev. edn. Oxford University Press.Google Scholar
Tian, S., Gao, Y., Dong, X. & Liu, C. 2018 Definitions of vortex vector and vortex. J. Fluid Mech. 849, 312-339.CrossRefGoogle Scholar
Tseng, H.-C. 2020 A revisitation of generalized Newtonian fluids. J. Rheol. 64, 493–504.CrossRefGoogle Scholar
Varchanis, S., Tsamopoulos, J., Shen, A.Q. & Haward, S.J. 2022 Reduced and increased flow resistance in shear-dominated flows of Oldroyd-B fluids. J. Non-Newtonian Fluid Mech. 300, 104698.CrossRefGoogle Scholar
Verhelst, J.M. & Nieuwstadt, F.T.M. 2004 Visco-elastic flow past cylinders mounted in a channel: experimental measurements of velocity and drag. J. Non-Newtonian Fluid Mech. 116, 301–328.CrossRefGoogle Scholar
Walters, K., Webster, M.F. & Tamaddon-Jahromi, H.R. 2009 The numerical simulation of some contraction flows of highly elastic liquids and their impact on the relevance of the Couette correction in extensional rheology. Chem. Engng Sci. 64, 4632–4639.CrossRefGoogle Scholar
White, S.A., Gotsis, A.D. & Baird, D.G. 1987 Review of the entry flow problem: experimental and numerical. J. Non-Newtonian Fluid Mech. 24, 121–160.CrossRefGoogle Scholar
Zografos, K., Afonso, A.M. & Poole, RJ. 2022 Viscoelastic simulations using the closed-form Adaptive Length Scale (ALS-C) model. J. Non-Newtonian Fluid Mech. 304, 104776.CrossRefGoogle Scholar