Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-27T19:35:34.068Z Has data issue: false hasContentIssue false
  • English
  • Français

Free-surface effects on the flow around two circular cylinders in tandem

Published online by Cambridge University Press:  05 December 2024

Feng Zhao Open the ORCID record for Feng Zhao [Opens in a new window] ,
Rui Wang ,
Hongbo Zhu Open the ORCID record for Hongbo Zhu [Opens in a new window] ,
Yong Cao Open the ORCID record for Yong Cao [Opens in a new window] ,
Yan Bao ,
Dai Zhou ,
Bin Cheng  and
Zhaolong Han
Feng Zhao
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Rui Wang
Affiliation:
School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, PR China
Hongbo Zhu
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Yong Cao
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Yan Bao*
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Dai Zhou
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Bin Cheng
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Zhaolong Han
Affiliation:
Department of Civil Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

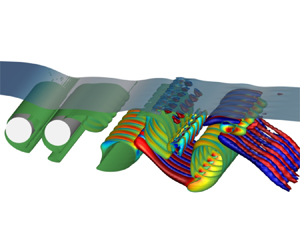
This paper presents a numerical study on the flow around two tandem circular cylinders beneath a free surface at a Reynolds number of $180$. The free-surface effects on the wake dynamics and hydrodynamic forces are investigated through a parametric study, covering a parameter space of gap ratios from $0.20$ to $2.00$, spacing ratios from $1.50$ to $4.00$ and Froude numbers from $0.2$ to $0.8$. A jet-like flow accompanied by a shear layer of positive vorticity separating from the free surface is formed in the wake at small gap ratios, which significantly alters the wake pattern through its dynamic behaviours. At shallow submergence depths, the three-dimensional wake transitions from mode B to mode A as the distance between the cylinders increases. As submergence depth increases, the wavy deformation of the primary vortex cores disappears in the wake, and the flow transitions to a two-dimensional state. Higher Froude numbers can extend the effect of the free surface to deeper submergence depths. The critical spacing ratio tends to be larger at higher Froude numbers. Furthermore, the free-surface deformation is examined. The free-surface profile typically comprises a hydraulic jump immediately ahead of the upstream cylinder, trapped waves in the vicinity of the two tandem cylinders and well-defined travelling waves on the downstream side. The frequencies of the waves cluster around the vortex shedding frequency, indicating a close association between the generation of waves and the vortex shedding process.

JFM classification

Vortex Flows: Vortex shedding Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A7
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aasland, T.E., Pettersen, B., Andersson, H.I. & Jiang, F. 2022 Revisiting the reattachment regime: a closer look at tandem cylinder flow at. J. Fluid Mech. 953, A18.CrossRefGoogle Scholar
Alam, M.M. 2014 The aerodynamics of a cylinder submerged in the wake of another. J. Fluids Struct. 51, 393–400.CrossRefGoogle Scholar
Alam, M.M. 2016 Lift forces induced by phase lag between the vortex sheddings from two tandem bluff bodies. J. Fluids Struct. 65, 217–237.CrossRefGoogle Scholar
Alam, M.M., Moriya, M., Takai, K. & Sakamoto, H. 2003 Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical reynolds number. J. Wind Engng Ind. Aerodyn. 91 (1–2), 139–154.CrossRefGoogle Scholar
Alam, M.M. & Zhou, Y. 2007 Phase lag between vortex shedding from two tandem bluff bodies. J. Fluids Struct. 23 (2), 339–347.CrossRefGoogle Scholar
Arie, M., Kiya, M., Moriya, M. & Mori, H. 1983 Pressure fluctuations on the surface of two circular cylinders in tandem arrangement. J. Fluids Engng 105 (2), 161–166.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bouscasse, B., Colagrossi, A., Marrone, S. & Souto-Iglesias, A. 2017 SPH modelling of viscous flow past a circular cylinder interacting with a free surface. Comput. Fluids 146, 190–212.CrossRefGoogle Scholar
Carmo, B.S. & Meneghini, J.R. 2006 Numerical investigation of the flow around two circular cylinders in tandem. J. Fluids Struct. 22 (6-7), 979–988.CrossRefGoogle Scholar
Carmo, B.S., Meneghini, J.R. & Sherwin, S.J. 2010 a Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing. Phys. Fluids 22 (5), 054101.CrossRefGoogle Scholar
Carmo, B.S., Meneghini, J.R. & Sherwin, S.J. 2010 b Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
Cetiner, O. & Rockwell, D. 2001 Streamwise oscillations of a cylinder in steady current. Part 2. Free-surface effects on vortex formation and loading. J. Fluid Mech. 427, 29–59.CrossRefGoogle Scholar
Chanson, H. 2004 Hydraulics of Open Channel Flow. Elsevier.Google Scholar
Chen, S., Zhao, W. & Wan, D. 2022 On the scattering of focused wave by a finite surface-piercing circular cylinder: a numerical investigation. Phys. Fluids 34 (3), 035132.CrossRefGoogle Scholar
Dagan, G. 1971 Free-surface gravity flow past a submerged cylinder. J. Fluid Mech. 49 (1), 179–192.CrossRefGoogle Scholar
Dias, F. & Vanden-Broeck, J.-M. 2004 Trapped waves between submerged obstacles. J. Fluid Mech. 509, 93–102.CrossRefGoogle Scholar
Fan, W. & Anglart, H. 2020 varRhoTurbVOF: a new set of volume of fluid solvers for turbulent isothermal multiphase flows in OpenFOAM. Comput. Phys. Commun. 247, 106876.CrossRefGoogle Scholar
González-Gutierrez, L.M., Gimenez, J.M. & Ferrer, E. 2019 Instability onset for submerged cylinders. Phys. Fluids 31 (1), 014106.CrossRefGoogle Scholar
Gopalan, H. & Jaiman, R. 2015 Numerical study of the flow interference between tandem cylinders employing non-linear hybrid URANS–LES methods. J. Wind Engng Ind. Aerodyn. 142, 111–129.CrossRefGoogle Scholar
Higuera, P., Liu, P.L.F., Lin, C., Wong, W.Y. & Kao, M.J. 2018 Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope. J. Fluid Mech. 847, 186–227.CrossRefGoogle Scholar
Hirt, C.W. & Nichols, B.D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.CrossRefGoogle Scholar
Hu, J.C. & Zhou, Y. 2008 Flow structure behind two staggered circular cylinders. Part 1. Downstream evolution and classification. J. Fluid Mech. 607, 51–80.CrossRefGoogle Scholar
Hu, X., Zhang, X. & You, Y. 2019 On the flow around two circular cylinders in tandem arrangement at high Reynolds numbers. Ocean Engng 189, 106301.CrossRefGoogle Scholar
Igarashi, T. 1981 Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bull. JSME 24 (188), 323–331.CrossRefGoogle Scholar
Igarashi, T. 1984 Characteristics of the flow around two circular cylinders arranged in tandem: 2nd report, unique phenomenon at small spacing. Bull. JSME 27 (233), 2380–2387.CrossRefGoogle Scholar
Issa, R.I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62 (1), 40–65.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017 Two-and three-dimensional instabilities in the wake of a circular cylinder near a moving wall. J. Fluid Mech. 812, 435–462.CrossRefGoogle Scholar
Kitagawa, T. & Ohta, H. 2008 Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number. J. Fluids Struct. 24 (5), 680–699.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Li, Z., Liu, C., Wan, D. & Hu, C. 2021 High-fidelity simulation of a hydraulic jump around a surface-piercing hydrofoil. Phys. Fluids 33 (12), 123304.CrossRefGoogle Scholar
Lin, J.-C., Yang, Y. & Rockwell, D. 2002 Flow past two cylinders in tandem: instantaneous and averaged flow structure. J. Fluids Struct. 16 (8), 1059–1071.CrossRefGoogle Scholar
Ljungkrona, L., Norberg, C.H. & Sundén, B. 1991 Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement. J. Fluids Struct. 5 (6), 701–727.CrossRefGoogle Scholar
Ljungkrona, L. & Sundén, B. 1993 Flow visualization and surface pressure measurement on two tubes in an inline arrangement. Exp. Therm. Fluid Sci. 6 (1), 15–27.CrossRefGoogle Scholar
Ma, Y., Xu, W., Zhai, L. & Ai, H. 2019 Hydrodynamic characteristics of two tandem flexible cylinders undergoing flow-induced vibration. Ocean Engng 193, 106587.CrossRefGoogle Scholar
Meneghini, J.R., Saltara, F., Siqueira, C.L.R. & Ferrari, J.A. Jr. 2001 Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15 (2), 327–350.CrossRefGoogle Scholar
Miyata, H., Shikazono, N. & Kanai, M. 1990 Forces on a circular cylinder advancing steadily beneath the free-surface. Ocean Engng 17 (1–2), 81–104.CrossRefGoogle Scholar
Moreira, R.M. & Peregrine, D.H. 2010 Nonlinear interactions between a free-surface flow with surface tension and a submerged cylinder. J. Fluid Mech. 648, 485–507.CrossRefGoogle Scholar
Okajima, A. 1979 Flows around two tandem circular cylinders at very high Reynolds numbers. Bull. JSME 22 (166), 504–511.CrossRefGoogle Scholar
Ong, M.C., Kamath, A., Bihs, H. & Afzal, M.S. 2017 Numerical simulation of free-surface waves past two semi-submerged horizontal circular cylinders in tandem. Mar. Struct. 52, 1–14.CrossRefGoogle Scholar
Page, C. & Părău, E.I. 2014 Hydraulic falls under a floating ice plate due to submerged obstructions. J. Fluid Mech. 745, 208–222.CrossRefGoogle Scholar
Papaioannou, G.V., Yue, D.K.P., Triantafyllou, M.S. & Karniadakis, G.E. 2006 Three-dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 558, 387–413.CrossRefGoogle Scholar
Phillips, O.M. 1966 The Dynamics of the Upper Ocean. Cambridge University Press.Google Scholar
Reichl, P., Hourigan, K. & Thompson, M.C. 2005 Flow past a cylinder close to a free surface. J. Fluid Mech. 533, 269.CrossRefGoogle Scholar
Sarpkaya, T. 1996 Vorticity, free surface, and surfactants. Annu. Rev. Fluid Mech. 28 (1), 83–128.CrossRefGoogle Scholar
Semenov, Y.A. & Wu, G.X. 2020 Free-surface gravity flow due to a submerged body in uniform current. J. Fluid Mech. 883, A60.CrossRefGoogle Scholar
Shelton, J. & Trinh, P.H. 2023 Exponential asymptotics and the generation of free-surface flows by submerged line vortices. J. Fluid Mech. 958, A29.CrossRefGoogle Scholar
Sheridan, J., Lin, J.-C. & Rockwell, D. 1997 Flow past a cylinder close to a free surface. J. Fluid Mech. 330, 1–30.CrossRefGoogle Scholar
Subburaj, R. & Vengadesan, S. 2019 Flow features for two cylinders arranged in tandem configuration near a free surface. J. Fluids Struct. 91, 102770.CrossRefGoogle Scholar
Sumner, D. 2010 Two circular cylinders in cross-flow: a review. J. Fluids Struct. 26 (6), 849–899.CrossRefGoogle Scholar
Sumner, D., Price, S.J. & Paidoussis, M.P. 2000 Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 411, 263–303.CrossRefGoogle Scholar
Tong, F., Cheng, L. & Zhao, M. 2015 Numerical simulations of steady flow past two cylinders in staggered arrangements. J. Fluid Mech. 765, 114–149.CrossRefGoogle Scholar
Tuck, E.O. 1965 The effect of non-linearity at the free surface on flow past a submerged cylinder. J. Fluid Mech. 22 (2), 401–414.CrossRefGoogle Scholar
Tuck, E.O. & Scullen, D.C. 1998 Tandem submerged cylinders each subject to zero drag. J. Fluid Mech. 364, 211–220.CrossRefGoogle Scholar
Wang, L., Alam, M.M. & Zhou, Y. 2018 Two tandem cylinders of different diameters in cross-flow: effect of an upstream cylinder on wake dynamics. J. Fluid Mech. 836, 5–42.CrossRefGoogle Scholar
Wang, Z., Chai, J., Părău, E.I., Page, C. & Wang, M. 2022 Trapped waves on interfacial hydraulic falls over bottom obstacles. Phys. Rev. Fluids 7 (7), 074801.CrossRefGoogle Scholar
Weller, H.G. 2008 A new approach to VOF-based interface capturing methods for incompressible and compressible flow. OpenCFD Tech. Rep. TR/HGW 4, p. 35. OpenCFD Ltd.Google Scholar
Wille, R. & Fernholz, H. 1965 Report on the first European mechanics colloquium, on the Coanda effect. J. Fluid Mech. 23 (4), 801–819.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Xu, G. & Zhou, Y. 2004 Strouhal numbers in the wake of two inline cylinders. Exp. Fluids 37, 248–256.CrossRefGoogle Scholar
Xu, W., Yu, Y., Wang, E. & Zhou, L. 2018 Flow-induced vibration (FIV) suppression of two tandem long flexible cylinders attached with helical strakes. Ocean Engng 169, 49–69.CrossRefGoogle Scholar
Yang, W. & Stremler, M.A. 2019 Critical spacing of stationary tandem circular cylinders at $Re \approx 100$. J. Fluids Struct. 89, 49–60.CrossRefGoogle Scholar
Yetik, Ö. & Mahir, N. 2020 Flow structure around two tandem square cylinders close to a free surface. Ocean Engng 214, 107740.CrossRefGoogle Scholar
Yu, D. & Tryggvason, G. 1990 The free-surface signature of unsteady, two-dimensional vortex flows. J. Fluid Mech. 218, 547–572.CrossRefGoogle Scholar
Zdravkovich, M.M. 1977 Review of flow interference between two circular cylinders in various arrangements. J. Fluids Engng 99 (4), 618–633.CrossRefGoogle Scholar
Zdravkovich, M.M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1 (2), 239–261.CrossRefGoogle Scholar
Zhang, H. & Melbourne, W.H. 1992 Interference between two circular cylinders in tandem in turbulent flow. J. Wind Engng Ind. Aerodyn. 41 (1–3), 589–600.CrossRefGoogle Scholar
Zhao, F., Wang, R., Zhu, H., Cao, Y., Bao, Y., Zhou, D. & Han, Z. 2022 Wake dynamics and hydrodynamic forces of a circular cylinder beneath a free surface. Ocean Engng 265, 112669.CrossRefGoogle Scholar
Zhao, F., Wang, R., Zhu, H., Ping, H., Bao, Y., Zhou, D., Cao, Y. & Cui, H. 2021 Large-eddy simulations of flow past a circular cylinder near a free surface. Phys. Fluids 33 (11), 115108.CrossRefGoogle Scholar
Zhao, M. & Cheng, L. 2014 Two-dimensional numerical study of vortex shedding regimes of oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds numbers. J. Fluid Mech. 751, 1–37.CrossRefGoogle Scholar
Zhou, Q., Alam, M.M., Cao, S., Liao, H. & Li, M. 2019 Numerical study of wake and aerodynamic forces on two tandem circular cylinders at $Re= 103$. Phys. Fluids 31 (4), 045103.CrossRefGoogle Scholar
Zhou, Y. & Alam, M.M. 2016 Wake of two interacting circular cylinders: a review. Intl J. Heat Fluid Flow 62, 510–537.CrossRefGoogle Scholar
Zhou, Y. & Yiu, M.W. 2006 Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 548, 17–48.CrossRefGoogle Scholar
Supplementary material: File

Zhao et al. supplementary movie 1

The temporal development of the wake at (Re, Fr, G, S)=(180, 0.6, 0.6, 3.0).
Download Zhao et al. supplementary movie 1(File)
File 1.5 MB
Supplementary material: File

Zhao et al. supplementary movie 2

Temporal development of the wake at (Re, Fr, G, S)=(7550, 0.6, 0.4, 2.5).
Download Zhao et al. supplementary movie 2(File)
File 2.3 MB
Supplementary material: File

Zhao et al. supplementary movie 3

The evolution of 3D flow structures at (Re, Fr, G, S)=(7550, 0.6, 0.4, 2.5).
Download Zhao et al. supplementary movie 3(File)
File 10.3 MB