Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-30T02:54:31.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Flame acceleration and detonation transition in premixed and inhomogeneous supersonic flows

Published online by Cambridge University Press:  13 December 2024

Wandong Zhao Open the ORCID record for Wandong Zhao [Opens in a new window] ,
Ralf Deiterding ,
Xiaodong Cai Open the ORCID record for Xiaodong Cai [Opens in a new window] ,
Jianhan Liang ,
Xiong Yang  and
Mingbo Sun Open the ORCID record for Mingbo Sun [Opens in a new window]
Wandong Zhao
Affiliation:
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, PR China
Ralf Deiterding
Affiliation:
AMROC CFD, Brookweg 167, 26127 Oldenburg, Germany
Xiaodong Cai
Affiliation:
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, PR China
Jianhan Liang*
Affiliation:
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, PR China
Xiong Yang
Affiliation:
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, PR China
Mingbo Sun*
Affiliation:
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, PR China
*
† Email addresses for correspondence: [email protected], [email protected]
† Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

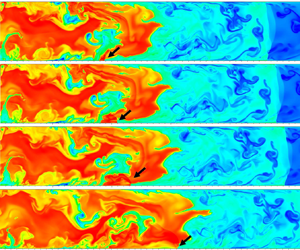
The reactive Navier–Stokes equations with adaptive mesh refinement and a detailed chemical reactive mechanism (11 species, 27 steps) were adopted to investigate a detonation engine considering the injection and supersonic mixing processes. Flame acceleration and deflagration-to-detonation transition (DDT) in a premixed/inhomogeneous supersonic hydrogen–air mixture with and without transverse jet obstacles were addressed. Results demonstrate the difficulty in undergoing DDT in the premixed/inhomogeneous supersonic mixture within a smooth chamber. By contrast, multiple transverse jets injected into the chamber aid detonation transition by introducing perturbed vortices, shock waves and a suitable blockage ratio. Increasing distance between the leading shock and the flame tip impedes detonation transition due to an insufficient blockage ratio. The extremely perturbed distributions of fuel-lean and fuel-rich mixtures lead to more complicated flame structures. Also, a larger flame thickness appears in the inhomogeneous mixture compared with the premixed mixture, resulting in a lower combustion temperature. The key findings are that the DDT, detonation quenching and reinitiation are generated in the inhomogeneous supersonic mixture, but both DDT mechanisms are ascribed to a strong Mach stem with the Zel'dovich gradient mechanism. Additionally, the obtained results demonstrate that an intensely fuel-lean mixture (equivalence ratio = 0.15) results in a partially decoupled flame front. However, detonation reinitiation and subsequent self-sustained detonation occur when a fierce shock wave propagates through a highly sensitive mixture, even within a smaller and elongated area. Moreover, the inhomogeneous mixture also augments the propagation speed and detonation cell structure instabilities and delays the sonic point resulting from the extending non-equilibrium reaction.

JFM classification

Compressible Flows: Detonation waves Reacting Flows: Detonations Reacting Flows: Combustion
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A36
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahmed, K.A. & Forliti, D.J. 2009 Fluidic flame stabilization in a planar combustor using a transverse slot jet. AIAA J. 47 (11), 2770–2775.CrossRefGoogle Scholar
Austin, J.M. 2003 The role of instability in gaseous detonation. PhD thesis, California Institute of Technology.Google Scholar
Azadboni, R.K., Heidari, A., Boeck, L.R. & Wen, J.X. 2019 The effect of concentration gradients on deflagration-to-detonation transition in a rectangular channel with and without obstructions – a numerical study. Intl J. Hydrogen Energy 44 (13), 7032–7040.CrossRefGoogle Scholar
Azadboni, R.K., Wen, J.X., Heidari, A. & Wang, C. 2017 Numerical modeling of deflagration to detonation transition in inhomogeneous hydrogen/air mixtures. J. Loss Prev. Process. Ind. 49, 722–730.CrossRefGoogle Scholar
Bird, R.B., Stewart, W.E. & Lightfoot, E.N. 2006 Transport Phenomena. John Wiley & Sons.Google Scholar
Boeck, L.R., Berger, F.M., Hasslberger, J. & Sattelmayer, T. 2016 Detonation propagation in hydrogen–air mixtures with transverse concentration gradients. Shock Waves 26 (2), 181–192.CrossRefGoogle Scholar
Boeck, L.R., Hasslberger, J. & Sattelmayer, T. 2014 Flame acceleration in hydrogen/air mixtures with concentration gradients. Combust. Sci. Technol. 186 (10–11), 1650–1661.CrossRefGoogle Scholar
Boivin, P., Jiménez, C., Sánchez, A.L. & Williams, F.A. 2011 An explicit reduced mechanism for H2–air combustion. Proc. Combust. Inst. 33 (1), 517–523.CrossRefGoogle Scholar
Boulal, S., Vidal, P. & Zitoun, R. 2016 Experimental investigation of detonation quenching in non-uniform compositions. Combust. Flame 172, 222–233.CrossRefGoogle Scholar
Burke, M., Chaos, M., Ju, Y., Dryer, F. & Klippenstein, S. 2012 Comprehensive H2/O2 kinetic model for high-pressure combustion. Intl J. Chem. Kinet. 44 (7), 444–474.CrossRefGoogle Scholar
Cai, X., Deiterding, R., Liang, J. & Mahmoudi, Y. 2017 Adaptive simulations of viscous detonations initiated by a hot jet using a high-order hybrid WENO–CD scheme. Proc. Combust. Inst. 36 (2), 2725–2733.CrossRefGoogle Scholar
Cai, X., Liang, J., Deiterding, R., Mahmoudi Larimi, Y. & Sun, M.-B. 2018 Experimental and numerical investigations on propagating modes of detonations: detonation wave/boundary layer interaction. Combust. Flame 190, 201–215.CrossRefGoogle Scholar
Cheng, J., Zhang, B., Liu, H. & Wang, F. 2020 Experimental study on the effects of different fluidic jets on the acceleration of deflagration prior its transition to detonation. Aerosp. Sci. Technol. 106, 106203.CrossRefGoogle Scholar
Cheng, J., Zhang, B., Liu, H. & Wang, F. 2021 a The precursor shock wave and flame propagation enhancement by CO2 injection in a methane-oxygen mixture. Fuel 283, 118917.CrossRefGoogle Scholar
Cheng, J., Zhang, B., Ng, D.H., Liu, H. & Wang, F. 2021 b Effects of inert gas jet on the transition from deflagration to detonation in a stoichiometric methane-oxygen mixture. Fuel 285, 119237.CrossRefGoogle Scholar
Cooper, M., Jackson, S., Austin, J., Wintenberger, E. & Shepherd, J. 2002 Direct experimental impulse measurements for detonations and deflagrations. J. Propul. Power 18 (5), 1033–1041.CrossRefGoogle Scholar
Deiterding, R. 2003 Parallel adaptive simulation of multi-dimensional detonation structures. PhD thesis, Brandenburgische Technische Universität Cottbus.Google Scholar
Deiterding, R. 2011 Block-structured adaptive mesh refinement-theory, implementation and application. Esaim: Proc. 34, 97–150.CrossRefGoogle Scholar
Ettner, F. 2013 Effiziente numerische Simulation des Deflagrations - Detonations - Übergangs. PhD thesis, Technische Universität München, München.Google Scholar
Ettner, F., Vollmer, K.G. & Sattelmayer, T. 2013 Mach reflection in detonations propagating through a gas with a concentration gradient. Shock Waves 23 (3), 201–206.CrossRefGoogle Scholar
Fan, J. & Xiao, H. 2022 Flame acceleration and transition to detonation in non-uniform hydrogen-air mixtures in an obstructed channel with different obstacle arrangements. Fire Safety J. 133, 103660.CrossRefGoogle Scholar
Fang, Y., Hu, Z., Teng, H., Jiang, Z. & Ng, H.D. 2017 Numerical study of inflow equivalence ratio inhomogeneity on oblique detonation formation in hydrogen–air mixtures. Aerosp. Sci. Technol. 71, 256–263.CrossRefGoogle Scholar
Fickett, W. & Davis, W.C. 2000 Detonation: Theory and Experiment. Courier Corporation.Google Scholar
Frolov, S.M., Smetanyuk, V.A., Aksenov, V.S. & Koval’, A.S. 2017 Deflagration-to-detonation transition in crossed-flow fast jets of propellant components. Dokl. Phys. Chem. 476 (1), 153–156.CrossRefGoogle Scholar
Gamezo, V.N., Bachman, C.L. & Oran, E.S. 2021 Flame acceleration and DDT in large-scale obstructed channels filled with methane-air mixtures. Proc. Combust. Inst. 38 (3), 3521–3528.CrossRefGoogle Scholar
Gamezo, V.N., Desbordes, D. & Oran, E.S. 1999 Formation and evolution of two-dimensional cellular detonations. Combust. Flame 116 (1–2), 154–165.CrossRefGoogle Scholar
Gamezo, V.N., Ogawa, T. & Oran, E.S. 2007 Numerical simulations of flame propagation and DDT in obstructed channels filled with hydrogen–air mixture. Proc. Combust. Inst. 31 (2), 2463–2471.CrossRefGoogle Scholar
Gamezo, V.N., Ogawa, T. & Oran, E.S. 2008 Flame acceleration and DDT in channels with obstacles: effect of obstacle spacing. Combust. Flame 155, 302–315.CrossRefGoogle Scholar
Goodwin, D.G., Moffat, H.K. & Speth, R.L. 2009 Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. Caltech.Google Scholar
Goodwin, G.B., Houim, R.W. & Oran, E.S. 2016 Effect of decreasing blockage ratio on DDT in small channels with obstacles. Combust. Flame 173, 16–26.CrossRefGoogle Scholar
Grogan, K.P. & Ihme, M. 2015 Weak and strong ignition of hydrogen/oxygen mixtures in shock-tube systems. Proc. Combust. Inst. 35 (2), 2181–2189.CrossRefGoogle Scholar
Grogan, K.P. & Ihme, M. 2017 Regimes describing shock boundary layer interaction and ignition in shock tubes. Proc. Combust. Inst. 36 (2), 2927–2935.CrossRefGoogle Scholar
Haghdoost, M.R., Edgington-Mitchell, D., Nadolski, M., Klein, R. & Oberleithner, K. 2020 Dynamic evolution of a transient supersonic trailing jet induced by a strong incident shock wave. Phys. Rev. Fluids 5 (7), 073401.CrossRefGoogle Scholar
Han, W., Huang, J., Gu, G., Wang, C. & Law, C.K. 2020 Surface heat loss and chemical kinetic response in deflagration-to-detonation transition in microchannels. Phys. Rev. Fluids 5 (5), 053201.CrossRefGoogle Scholar
Han, W., Wang, C. & Law, C.K. 2019 Role of transversal concentration gradient in detonation propagation. J. Fluid Mech. 865, 602–649.CrossRefGoogle Scholar
Hu, X., Zhang, D., Khoo, B.C. & Jiang, Z. 2005 The structure and evolution of a two-dimensional H2/O2/Ar cellular detonation. Shock Waves 14 (1), 37–44.CrossRefGoogle Scholar
Ishii, K. & Kojima, M. 2007 Behavior of detonation propagation in mixtures with concentration gradients. Shock Waves 17 (1–2), 95–102.CrossRefGoogle Scholar
Ivanov, M.F., Kiverin, A.D. & Liberman, M.A. 2011 Hydrogen-oxygen flame acceleration and transition to detonation in channels with no-slip walls for a detailed chemical reaction model. Phys. Rev. E Stat. Nonlinear 83 (5), 056313.CrossRefGoogle ScholarPubMed
Iwata, K., Imamura, O., Akihama, K., Yamasaki, H., Nakaya, S. & Tsue, M. 2021 Numerical study of self-sustained oblique detonation in a non-uniform mixture. Proc. Combust. Inst. 38 (3), 3651–3659.CrossRefGoogle Scholar
Iwata, K., Nakaya, S. & Tsue, M. 2017 Wedge-stabilized oblique detonation in an inhomogeneous hydrogen–air mixture. Proc. Combust. Inst. 36 (2), 2761–2769.CrossRefGoogle Scholar
Jachimowski, C.J. 1988 An analytical study of the hydrogen-air reaction mechanism with application to scramjet combustion. No. L-16372.Google Scholar
Jiang, C., Pan, J., Weng, J., Li, J. & Quaye, E.K. 2022 a Role of concentration gradient in the re-initiation of H2/O2 detonation in a 90° bifurcated channel. Aerosp. Sci. Technol. 120, 107281.CrossRefGoogle Scholar
Jiang, C., Pan, J., Zhu, Y., Li, J., Chen, H. & Quaye, E.K. 2022 b Influence of concentration gradient on detonation re-initiation in a bifurcated channel. Fuel 307, 121895.CrossRefGoogle Scholar
Kaps, P. & Rentrop, P. 1979 Generalized Runge-Kutta methods of order four with stepsize control for stiff ordinary differential equations. Numer. Math. 33 (1), 55–68.CrossRefGoogle Scholar
Kessler, D.A., Gamezo, V.N. & Oran, E.S. 2010 Simulations of flame acceleration and deflagration-to-detonation transitions in methane-air systems. Combust. Flame 157, 2063–2077.CrossRefGoogle Scholar
Kessler, D.A., Gamezo, V.N. & Oran, E.S. 2011 Detonation propagation through a gradient in fuel composition. In Paper presented at the Proceedings of the 23th International Colloquium on the Dynamics of Explosions and Reacting Systems, Irvine, CA.Google Scholar
Kessler, D.A., Gamezo, V.N. & Oran, E.S. 2012 Gas-phase detonation propagation in mixture composition gradients. Phil. Trans. R. Soc. A: Math. Phys. Engng Sci. 370 (1960), 567–596.CrossRefGoogle ScholarPubMed
Knox, B., Forliti, D., Stevens, C., Hoke, J. & Schauer, F. 2011 A comparison of fluidic and physical obstacles for deflagration-to-detonation transition. In 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 587.Google Scholar
Kuznetsov, M.S., Alekseev, V.I., Dorofeev, S.B., Matsukov, I.D. & Boccio, J.L. 1998 Detonation propagation, decay, and reinitiation in nonuniform gaseous mixtures. Symp. (Intl) Combust. 27 (2), 2241–2247.CrossRefGoogle Scholar
Law, C.K. 2010 Combustion Physics. Cambridge University Press.Google Scholar
Lee, J., Knystautas, R. & Yoshikawa, N. 1980 Photochemical initiation of gaseous detonations. In Gas Dynamics of Explosions and Reactive Systems, pp. 971–982. Elsevier.CrossRefGoogle Scholar
Lehr, H.F. 1972 Experiments on shock-induced combustion. Astr. Acta 17, 589–597.Google Scholar
Li, T., Wang, X., Xu, B. & Kong, F. 2021 An efficient approach to achieve flame acceleration and transition to detonation. Phys. Fluids 33 (5), 056103.CrossRefGoogle Scholar
Li, X. & Zhang, Q. 1997 A comparative numerical study of the Richtmyer-Meshkov instability with nonlinear analysis in two and three dimensions. Phys. Fluids 9, 3069–3077.CrossRefGoogle Scholar
Luan, Z., Huang, Y., Gao, S. & You, Y. 2022 Formation of multiple detonation waves in rotating detonation engines with inhomogeneous methane/oxygen mixtures under different equivalence ratios. Combust. Flame 241, 112091.CrossRefGoogle Scholar
Mahmoudi, Y., Karimi, N., Deiterding, R. & Emami, S. 2014 Hydrodynamic instabilities in gaseous detonations: comparison of Euler, Navier–Stokes, and large-eddy simulation. J. Propul. Power 30 (2), 384–396.CrossRefGoogle Scholar
Mahmoudi, Y. & Mazaheri, K. 2011 High resolution numerical simulation of the structure of 2-D gaseous detonations. Proc. Combust. Inst. 33 (2), 2187–2194.CrossRefGoogle Scholar
Mahmoudi, Y. & Mazaheri, K. 2015 High resolution numerical simulation of triple point collision and origin of unburned gas pockets in turbulent detonations. Acta Astronaut. 115, 40–51.CrossRefGoogle Scholar
Mathur, S., Tondon, P. & Saxena, S. 1967 Thermal conductivity of binary, ternary and quaternary mixtures of rare gases. Mol. Phys. 12 (6), 569–579.CrossRefGoogle Scholar
McGarry, J.P. & Ahmed, K.A. 2017 Flame–turbulence interaction of laminar premixed deflagrated flames. Combust. Flame 176, 439–450.CrossRefGoogle Scholar
Metrow, C., Gray, S. & Ciccarelli, G. 2021 Detonation propagation through a nonuniform layer of hydrogen-oxygen in a narrow channel. Intl J. Hydrogen Energy 46 (41), 21726–21738.CrossRefGoogle Scholar
Mi, X., Higgins, A., Ng, H.D., Kiyanda, C. & Nikiforakis, N. 2017 Propagation of gaseous detonation waves in a spatially inhomogeneous reactive medium. Phys. Rev. Fluids 2 (5), 053201.CrossRefGoogle Scholar
Ng, H.D., Ju, Y. & Lee, J.H. 2007 Assessment of detonation hazards in high-pressure hydrogen storage from chemical sensitivity analysis. Intl J. Hydrogen Energy 32 (1), 93–99.CrossRefGoogle Scholar
Ogawa, T., Gamezo, V.N. & Oran, E.S. 2013 Flame acceleration and transition to detonation in an array of square obstacles. J. Loss Prev. Process Ind. 26 (2), 355–362.CrossRefGoogle Scholar
Oran, E.S., Chamberlain, G. & Pekalski, A. 2020 Mechanisms and occurrence of detonations in vapor cloud explosions. Prog. Energy Combust. Sci. 77, 100804.CrossRefGoogle Scholar
Oran, E.S., Jones, D.A. & Sichel, M. 1992 Numerical simulations of detonation transmission. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci. 436 (1897), 267–297.Google Scholar
Peng, H., Huang, Y., Deiterding, R., Luan, Z., Xing, F. & You, Y. 2018 Effects of jet in crossflow on flame acceleration and deflagration to detonation transition in methane–oxygen mixture. Combust. Flame 198, 69–80.CrossRefGoogle Scholar
Peng, H., Huang, Y., Deiterding, R., You, Y. & Luan, Z. 2019 Effects of transverse jet parameters on flame propagation and detonation transition in hydrogen–oxygen–argon mixture. Combust. Sci. Technol. 00, 1–22.Google Scholar
Radulescu, M.I., Sharpe, G.J., Law, C.K. & Lee, J.H. 2007 The hydrodynamic structure of unstable cellular detonations. J. Fluid Mech. 580, 31–81.CrossRefGoogle Scholar
Radulescu, M.I., Sharpe, G.J., Lee, J., Kiyanda, C., Higgins, A. & Hanson, R. 2005 The ignition mechanism in irregular structure gaseous detonations. Proc. Combust. Inst. 30 (2), 1859–1867.CrossRefGoogle Scholar
Roy, G.D., Frolov, S.M., Borisov, A.A. & Netzer, D.W. 2004 Pulse detonation propulsion: challenges, current status, and future perspective. Prog. Energy Combust. Sci. 30 (6), 545–672.CrossRefGoogle Scholar
Saeid, M.H.S., Khadem, J. & Emami, S. 2021 Numerical investigation of the mechanism behind the deflagration to detonation transition in homogeneous and inhomogeneous mixtures of H2-air in an obstructed channel. Intl J. Hydrogen Energy 46 (41), 21657–21671.CrossRefGoogle Scholar
Saeid, M.H.S., Khadem, J., Emami, S. & Ghodrat, M. 2022 Effect of diffusion time on the mechanism of deflagration to detonation transition in an inhomogeneous mixture of hydrogen-air. Intl J. Hydrogen Energy 47 (55), 23411–23426.CrossRefGoogle Scholar
Sharpe, G.J. 2001 Transverse waves in numerical simulations of cellular detonations. J. Fluid Mech. 447, 31–51.CrossRefGoogle Scholar
Sochet, I., Lamy, T. & Brossard, J. 2000 Experimental investigation on the detonability of non-uniform gaseous mixtures. Shock Waves 10 (5), 363–376.CrossRefGoogle Scholar
Song, Q., Han, Y. & Cao, W. 2020 Numerical investigation of self-sustaining modes of 2D planar detonations under concentration gradients in hydrogen–oxygen mixtures. Intl J. Hydrogen Energy 45 (53), 29606–29615.CrossRefGoogle Scholar
Subbotin, V. 1975 Two kinds of transverse wave structures in multifront detonation. Combust. Explos. Shock Waves 11 (1), 83–88.CrossRefGoogle Scholar
Sun, X. & Lu, S. 2020 On the mechanisms of flame propagation in methane-air mixtures with concentration gradient. Energy 202, 117782.CrossRefGoogle Scholar
Tang-Yuk, K.C., Mi, X., Lee, J.H.S., Ng, H.D. & Deiterding, R. 2022 Transmission of a detonation wave across an inert layer. Combust. Flame 236, 111769.CrossRefGoogle Scholar
Tarrant, D.J., Chambers, J.M., Joo, P.H. & Ahmed, K. 2020 Influence of transverse slot jet on premixed flame acceleration. J. Propul. Power 36, 59–67.CrossRefGoogle Scholar
Thomas, G.O., Sutton, P. & Edwards, D.H. 1991 The behavior of detonation waves at concentration gradients. Combust. Flame 84 (3–4), 312–322.CrossRefGoogle Scholar
Vollmer, K., Ettner, F. & Sattelmayer, T. 2012 Deflagration-to-detonation transition in hydrogen-air mixtures with a concentration gradient. Combust. Sci. Technol. 184 (10–11), 1903–1905.CrossRefGoogle Scholar
Wang, C.J. & Wen, J.X. 2017 Numerical simulation of flame acceleration and deflagration-to-detonation transition in hydrogen-air mixtures with concentration gradients. Intl J. Hydrogen Energy 42 (11), 7657–7663.CrossRefGoogle Scholar
Wang, Y., Huang, C., Deiterding, R., Chen, H. & Chen, Z. 2020 Propagation of gaseous detonation across inert layers. Proc. Combust. Inst. 38, 3555–3563.CrossRefGoogle Scholar
Xiao, H. & Oran, E.S. 2019 Shock focusing and detonation initiation at a flame front. Combust. Flame 203, 397–406.CrossRefGoogle Scholar
Xiao, H. & Oran, E.S. 2020 Flame acceleration and deflagration-to-detonation transition in hydrogen-air mixture in a channel with an array of obstacles of different shapes. Combust. Flame 220, 378–393.CrossRefGoogle Scholar
Yao, K., Yang, P., Teng, H., Chen, Z. & Wang, C. 2022 Effects of injection parameters on propagation patterns of hydrogen-fueled rotating detonation waves. Intl J. Hydrogen Energy 47 (91), 38811–38822.CrossRefGoogle Scholar
Yhuel, E., Ribert, G. & Domingo, P. 2023 Numerical simulation of laminar premixed hydrogen-air flame/shock interaction in semi-closed channel. Proc. Combust. Inst. 39 (3), 3021–3029.CrossRefGoogle Scholar
Yuan, X., Zhou, J., Mi, X. & Ng, H.D. 2019 Numerical study of cellular detonation wave reflection over a cylindrical concave wedge. Combust. Flame 202, 179–194.CrossRefGoogle Scholar
Zel'Dovich, Y.B., Librovich, V.B., Makhviladze, G.M. & Sivashinsky, G.I. 1970 On the development of detonation in a non-uniformly preheated gas. Astronaut. Acta 15 (5), 313–321.Google Scholar
Zhang, L., Qiao, H., Liang, J., Wang, Y., Ding, M., Yang, L. & Sun, M. 2024 Experimental study of scramjet cavity with rear edge slots and its performance in combustion enhancement. Acta Mechanica Sin. 40 (1), 323135.CrossRefGoogle Scholar
Zhao, W., Deiterding, R., Liang, J., Cai, X. & Wang, X. 2023 a Detonation simulations in supersonic flow under circumstances of injection and mixing. Proc. Combust. Inst. 39 (3), 2895–2903.CrossRefGoogle Scholar
Zhao, W., Deiterding, R., Liang, J., Wang, X., Cai, X. & Duell, J. 2023 b Adaptive simulations of flame acceleration and detonation transition in subsonic and supersonic mixtures. Aerosp. Sci. Technol. 136, 108205.CrossRefGoogle Scholar
Zhao, W., Fan, C., Deiterding, R., Li, X., Liang, J. & Yang, X. 2024 A new rapid deflagration-to-detonation transition in a short smooth tube. Phys. Fluids 36 (3), 036104.CrossRefGoogle Scholar
Zhao, W., Liang, J., Deiterding, R., Cai, X. & Wang, X. 2021 Effect of transverse jet position on flame propagation regime. Phys. Fluids 33 (9), 091704.CrossRefGoogle Scholar
Zhao, W., Liang, J., Deiterding, R., Cai, X. & Wang, X. 2022 a Flame–turbulence interactions during flame acceleration using solid and fluid obstacles. Phys. Fluids 34 (10), 106106.CrossRefGoogle Scholar
Zhao, X., Wang, J., Gao, L., Wang, X. & Zhu, Y. 2022 b Flame acceleration and onset of detonation in inhomogeneous mixture of hydrogen-air in an obstructed channel. Aerosp. Sci. Technol. 130, 107944.CrossRefGoogle Scholar
Zheng, W., Kaplan, C.R., Houim, R.W. & Oran, E.S. 2019 Flame acceleration and transition to detonation: effects of a composition gradient in a mixture of methane and air. Proc. Combust. Inst. 37 (3), 3521–3528.CrossRefGoogle Scholar