Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-28T14:47:43.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of random roughness on Stokes flow

Published online by Cambridge University Press:  25 November 2024

Gerardo Severino Open the ORCID record for Gerardo Severino [Opens in a new window]
Gerardo Severino*
Affiliation:
Division of Water Resources Management, University of Naples - Federico II, via Universitá 100, Portici, I80055 NA, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

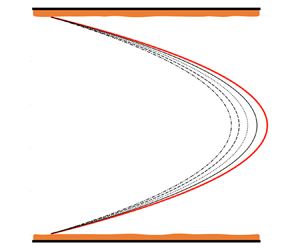
Microscopic irregularity (roughness) of bounding surfaces affects macroscopic dynamics of fluid flows. Its effect on bulk flow is usually quantified empirically by means of a roughness coefficient. A new approach, which treats rough surfaces (e.g. parallel plates) as random fields whose statistical properties can be inferred from measurements, is presented. The mapping of a random flow domain onto its deterministic counterpart, and the subsequent stochastic averaging of the transformed Stokes equations, yield expressions for the effective viscosity and roughness coefficient in terms of the statistical characteristics of the irregular geometry of the boundaries. The analytical nature of the solutions allows one to handle surface roughness characterized by short correlation lengths, a challenging feature for numerical stochastic simulations.

JFM classification

Low-Reynolds-number flows: Stokesian dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , R1
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arfken, G.B. & Weber, H.J. 2005 Mathematical Methods for Physicists, 6th edn. Academic.Google Scholar
Bahrami, M.M., Yovanovich, M.M. & Culham, J.R. 2006 a Pressure drop of fully-developed, laminar flow in microchannels of arbitrary cross-section. ASME J. Fluids Engng 128 (5), 1036–1044.CrossRefGoogle Scholar
Bahrami, M.M., Yovanovich, M.M. & Culham, J.R. 2006 b Pressure drop of fully developed, laminar flow in rough microtubes. ASME. J. Fluids Engng 128 (1), 632–637.CrossRefGoogle Scholar
Brown, S.R. 1987 Fluid flow through rock joints: the effect of surface roughness. J. Geophys. Res. Solid Earth 92 (B2), 1337–1347.CrossRefGoogle Scholar
Brown, S.R. 1989 Transport of fluid and electric current through a single fracture. J. Geophys. Res. Solid Earth 94 (B7), 9429–9438.CrossRefGoogle Scholar
Brown, S.R., Stockman, H.W. & Reeves, S.J. 1995 Applicability of the Reynolds equation for modeling fluid flow between rough surfaces. Geophys. Res. Lett. 22 (18), 2537–2540.CrossRefGoogle Scholar
Chen, Y., Zhang, C., Shi, M. & Peterson, G.P. 2009 Role of surface roughness characterized by fractal geometry on laminar flow in microchannels. Phys. Rev. E 80 (2), 026301.CrossRefGoogle ScholarPubMed
Dewangan, M.K. 2024 Investigation of Stokes flow in a grooved channel using the spectral method. Theor. Comput. Fluid Dyn. 38 (1), 39–59.CrossRefGoogle Scholar
Gamrat, G., Favre-Marinet, M., Le Person, S., Baviere, R. & Ayela, F. 2008 An experimental study and modelling of roughness effects on laminar flow in microchannels. J. Fluid Mech. 594, 399–423.CrossRefGoogle Scholar
Herwig, H., Gloss, D. & Wenterodt, T. 2008 A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 613 (1), 35–53.CrossRefGoogle Scholar
Hightower, C.M., et al. 2011 Integration of cardiovascular regulation by the blood/endothelium cell-free layer. WIREs Syst. Biol. Med. 3 (4), 458–470.CrossRefGoogle ScholarPubMed
Kandlikar, S.G., Schmitt, D., Carrano, A.L. & Taylor, J.B. 2005 Characterization of surface roughness effects on pressure drop in single-phase flow in minichannels. Phys. Fluids 17 (10), 100606.CrossRefGoogle Scholar
Kwon, C. & Tartakovsky, D.M. 2020 Modified immersed boundary method for flows over randomly rough surfaces. J. Comput. Phys. 406, 109195.CrossRefGoogle Scholar
Lenci, A., Méheust, Y., Putti, M. & Di Federico, V. 2022 Monte Carlo simulations of shear-thinning flow in geological fractures. Water Resour. Res. 58 (9), e2022WR032024.CrossRefGoogle Scholar
Li, H., Fu, P., Zhou, Z., Sun, W., Li, Y., Wu, J. & Dai, Q. 2022 Performing calculus with epsilon-near-zero metamaterials. Sci. Adv. 8, eabq6198.CrossRefGoogle ScholarPubMed
Maggiolo, D., Manes, C. & Marion, A. 2013 Momentum transport and laminar friction in rough-wall duct flows. Phys. Fluid 25 (9), 093603.CrossRefGoogle Scholar
Moody, L.F. 1944 Friction factors for pipe flow. Trans. ASME 66 (8), 671–684.Google Scholar
Murthy, A.N., Duwensee, M. & Talke, F.E. 2010 Numerical simulation of the head/disk interface for patterned media. Tribol. Lett. 38, 47–55.CrossRefGoogle Scholar
Navajas, D., Pérez-Escudero, J.M., Martínez-Hernández, M.E., Goicoechea, J. & Liberal, I. 2023 Addressing the impact of surface roughness on epsilon-near-zero silicon carbide substrates. ACS Photonics 10, 3105–3114.CrossRefGoogle ScholarPubMed
Nawaz, H., Masood, M.U., Saleem, M.M., Iqbal, J. & Zubair, M. 2020 Surface roughness effects on electromechanical performance of RF-MEMS capacitive switches. Microelectron. Reliab. 104, 113544.CrossRefGoogle Scholar
Owen, D.G., Schenkel, T., Shepherd, D.E.T. & Espino, D.M. 2020 Assessment of surface roughness and blood rheology on local coronary haemodynamics: a multi-scale computational fluid dynamics study. J. R. Soc. Interface 17 (169), 20200327.CrossRefGoogle ScholarPubMed
Park, S.-W., Intaglietta, M. & Tartakovsky, D.M. 2012 Impact of endothelium roughness on blood flow. J. Theor. Biol. 300, 152–160.CrossRefGoogle ScholarPubMed
Park, S.-W., Intaglietta, M. & Tartakovsky, D.M. 2015 Impact of stochastic fluctuations in the cell free layer on nitric oxide bioavailability. Front. Comput. Neurosci. 9, 131.CrossRefGoogle ScholarPubMed
Plouraboué, F., Geoffroy, S. & Prat, M. 2004 Conductances between confined rough walls. Phys. Fluids 16 (3), 615–624.CrossRefGoogle Scholar
Severino, G. & De Bartolo, S. 2015 Stochastic analysis of steady seepage underneath a water-retaining wall through highly anisotropic porous media. J. Fluid Mech. 778, 253–272.CrossRefGoogle Scholar
Severino, G., Giannino, F., De Paola, F. & Di Federico, V. 2023 Effective conductivity of inertial flows through porous media. Phys. Rev. E 107, 035102.CrossRefGoogle ScholarPubMed
Tartakovsky, D.M. & Xiu, D. 2006 Stochastic analysis of transport in tubes with rough walls. J. Comput. Phys. 217 (1), 248–259.CrossRefGoogle Scholar
Tavakol, B., Froehlicher, G., Holmes, D.P. & Stone, H.A. 2017 Extended lubrication theory: improved estimates of flow in channels with variable geometry. Proc. R. Soc. A 473 (2206), 20170234.CrossRefGoogle ScholarPubMed
Viswanathan, H.S., et al. 2022 From fluid flow to coupled processes in fractured rock: recent advances and new frontiers. Rev. Geophys. 60 (1), e2021RG000744.CrossRefGoogle Scholar
Wang, X.-Q., Yap, C. & Mujumdar, A.S. 2005 Effects of two-dimensional roughness in flow in microchannels. J. Electron. Packag. 127 (3), 357–361.CrossRefGoogle Scholar
Webb, R.L. & Kim, N.-H. 1994 Principles of Enhanced Heat Transfer. Taylor Francis.Google Scholar
Xiu, D. & Tartakovsky, D.M. 2006 Numerical methods for differential equations in random domains. SIAM J. Sci. Comput. 28 (3), 1167–1185.CrossRefGoogle Scholar
Yaglom, A.M. 1987 Correlation Theory of Stationary and Related Random Functions. I. Basic Results. Springer.Google Scholar
Yamane, R., Mori, S., Arakawa, M., Wilhjelm, J.E. & Kanai, H. 2023 Ultrasonic measurement of carotid luminal surface roughness with removal of axial displacement caused by blood pulsation. Japan. J. Appl. Phys. 62, SJ1042.CrossRefGoogle Scholar
Yi, J., Tian, F.-B., Simmons, A. & Barber, T. 2022 Impact of modelling surface roughness in an arterial stenosis. Fluids 7 (5), 179.CrossRefGoogle Scholar
Zayernouri, M., Park, S.-W., Tartakovsky, D.M. & Karniadakis, G.E. 2013 Stochastic smoothed profile method for modeling random roughness in flow problems. Comput. Meth. Appl. Mech. Engng 263, 99–112.CrossRefGoogle Scholar
Zheng, Z., Valdebenito, M., Beer, M. & Nackenhorst, U. 2023 A stochastic finite element scheme for solving partial differential equations defined on random domains. Comput. Meth. Appl. Mech. Engng 405, 115860.CrossRefGoogle Scholar