Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-29T13:50:30.169Z Has data issue: false hasContentIssue false
  • English
  • Français

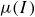A depth-averaged model for granular flow consistent with the incompressible $\mu (I)$ rheology

Published online by Cambridge University Press:  28 April 2025

Emile Deléage Open the ORCID record for Emile Deléage [Opens in a new window]  and
Gaël Loïc Richard Open the ORCID record for Gaël Loïc Richard [Opens in a new window]
Emile Deléage
Affiliation:
Aix Marseille Univ., CNRS, Centrale Marseille, I2M UMR CNRS 7373, 13003 Marseille, France Univ. Grenoble Alpes, INRAE, IGE, 38000 Grenoble, France
Gaël Loïc Richard*
Affiliation:
Univ. Grenoble Alpes, INRAE, IGE, 38000 Grenoble, France
*
Corresponding author: Gaël Loïc Richard, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive a depth-averaged model consistent with the $\mu (I)$ rheology for an incompressible granular flow down an inclined plane. The first two variables of the model are the depth and the depth-averaged velocity. The shear is also taken into account via a third variable called enstrophy. The obtained system is a hyperbolic system of conservation laws, with an additional equation for the energy. The system is derived from an asymptotic expansion of the flow variables in powers of the shallow-water parameter. This method ensures that the model is fully consistent with the rheology. The velocity profile is a Bagnold profile at leading order and the first-order correction to this profile can be calculated for flows that are not steady uniform. The first-order correction to the classical granular friction law is also consistently written. As a consequence, the instability threshold of the steady uniform flow is the same for the depth-averaged model and for the governing equations. In addition, a higher-order version that contains diffusive terms is also presented. The spatial growth rate, the phase velocity and the cutoff frequency of the version with diffusion are in good agreement with the experimental data and with the theoretical predictions for the rheology. The mathematical structure of the equations enables us to use well-known and stable numerical solvers. Numerical simulations of granular roll waves are presented. The model has the same limitations as the $\mu (I)$ rheology, in particular for the solid/ liquid and liquid/gas transitions, and needs therefore a regularisation for these transitions.

JFM classification

Geophysical and Geological Flows: Shallow water flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1009 , 25 April 2025 , A57
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andreotti, B., Forterre, Y. & Pouliquen, O. 2013 Granular Media, Between Fluid and Solid. Cambridge University Press.CrossRefGoogle Scholar
Baker, J.L., Barker, T. & Gray, J.M.N.T. 2016 a A two-dimensional depth-averaged-rheology for dense granular avalanches. J. Fluid Mech. 787, 367–395.CrossRefGoogle Scholar
Baker, J.L., Johnson, C.G. & Gray, J.M.N.T. 2016 b Segregation-induced finger formation in granular free-surface flows. J. Fluid Mech. 809, 168–212.CrossRefGoogle Scholar
Barker, T. & Gray, J.M.N.T. 2017 Partial regularisation of the incompressible $\mu (i)$ -rheology for granular flow. J. Fluid Mech. 828, 5–32.CrossRefGoogle Scholar
Barker, T., Schaeffer, D.G., Bohórquez, P. & Gray, J.M.N.T. 2015 Well-posed and ill-posed behaviour of the μ(I)-rheology for granular flow. J. Fluid Mech. 779, 794–818.CrossRefGoogle Scholar
Barker, T., Schaeffer, D.G., Shearer, M. & Gray, J.M.N.T. 2017 Well-posed continuum equations for granular flow with compressibility and $\mu$ (i)-rheology (i)-rheology (i)-rheology (i)-rheology. Proc. R. Soc. Lond. A Math. Phys. Engng Sci. 473 (2201), 20160846.Google Scholar
Börzsönyi, T. & Ecke, R.E. 2006 Rapid granular flows on a rough incline: phase diagram, gas transition, and effects of air drag. Phys. Rev. E 74 (6), 061301.CrossRefGoogle ScholarPubMed
Börzsönyi, T., Halsey, T.C. & Ecke, R.E. 2005 Two scenarios for avalanche dynamics in inclined granular layers. Phys. Rev. Lett. 94 (20), 208001.CrossRefGoogle ScholarPubMed
Bouchut, F. & Westdickenberg, M. 2004 Gravity driven shallow water models for arbitrary topography. Commun. Math. Sci. 2 (3), 359–389.CrossRefGoogle Scholar
Bouzid, M., Izzet, A., Trulsson, M., Clément, E., Claudin, P. & Andreotti, B. 2015 Non-local rheology in dense granular flows: revisiting the concept of fluidity. Eur. Phys. J. (E) 38 (11), 1–15.Google ScholarPubMed
Denisenko, D., Richard, G.L. & Chambon, G. 2023 A consistent three-equation shallow-flow model for Bingham fluids. J. Non-Newtonian Fluid Mech. 321, 105111.CrossRefGoogle Scholar
Denlinger, R.P. & Iverson, R.M. 2001 Flow of variably fluidized granular masses across three-dimensional terrain: 2. Numerical predictions and experimental tests. J. Geophys. Res.: Solid Earth 106 (B1), 553–566.CrossRefGoogle Scholar
Denlinger, R.P. & Iverson, R.M. 2004 Granular avalanches across irregular three-dimensional terrain: 1. Theory and computation. J. Geophys. Res. 109, F01014.CrossRefGoogle Scholar
Edwards, A.N. & Gray, J.M.N.T. 2015 Erosion–deposition waves in shallow granular free-surface flows. J. Fluid Mech. 762, 35–67.CrossRefGoogle Scholar
Edwards, A.N., Viroulet, S., Kokelaar, B.P. & Gray, J.M.N.T. 2017 Formation of levees, troughs and elevated channels by avalanches on erodible slopes. J. Fluid Mech. 823, 278–315.CrossRefGoogle Scholar
Forterre, Y. 2006 Kapiza waves as a test for three-dimensional granular flow rheology. J. Fluid Mech. 563, 123–132.CrossRefGoogle Scholar
Forterre, Y. & Pouliquen, O. 2003 Long-surface-wave instability in dense granular flows. J. Fluid Mech. 486, 21–50.CrossRefGoogle Scholar
Gaume, J., Chambon, G. & Naaim, M. 2020 Microscopic origin of nonlocal rheology in dense granular materials. Phys. Rev. Lett. 125 (18), 188001.CrossRefGoogle ScholarPubMed
GDR MiDi. 2004 On dense granular flows. Eur. Phys. J. (E) 14 (4), 341–365.Google Scholar
Goddard, J.D. & Lee, J. 2017 On the stability of the $\mu$ (i) rheology for granular flow. J. Fluid Mech. 833, 302–331.CrossRefGoogle Scholar
Goddard, J.D. & Lee, J. 2018 Regularization by compressibility of the $\mu$ (i) model of dense granular flow. Phys. Fluids 30, 073302.CrossRefGoogle Scholar
Gray, J. & Edwards, A. 2014 A depth-averaged $\mu ({I})$ -rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 297–329.CrossRefGoogle Scholar
Heyman, J., Delannay, R., Tabuteau, H. & Valance, A. 2017 Compressibility regularizes the $\mu (I)$ -rheology for dense granular flows. J. Fluid Mech. 830, 553–568.CrossRefGoogle Scholar
Holyoake, A.J. & McElwaine, J.N. 2012 High-speed granular chute flows. J. Fluid Mech. 710, 35–71.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.CrossRefGoogle ScholarPubMed
Kamrin, K. 2019 Non-locality in granular flow: phenomenology and modeling approaches. Frontiers Phys. 7, 116.CrossRefGoogle Scholar
Kamrin, K. & Henann, D.L. 2015 Nonlocal modeling of granular flows down inclines. Soft Matt. 11 (1), 179–185.CrossRefGoogle ScholarPubMed
Kamrin, K. & Koval, G. 2012 Nonlocal constitutive relation for steady granular flow. Phys. Rev. Lett. 108 (17), 178301.CrossRefGoogle ScholarPubMed
Lagrée, P.-Y., Saingier, G., Deboeuf, S., Staron, L. & Popinet, S. 2017 Granular front for flow down a rough incline: about the value of the shape factor in depths averaged models. In EPJ Web of Conferences, pp. 03046. EDP Sciences. vol. 140.Google Scholar
Larrieu, E., Staron, L. & Hinch, E.J. 2006 Raining into shallow water as a description of the collapse of a column of grains. J. Fluid Mech. 554, 259–270.CrossRefGoogle Scholar
Mangeney, A., Bouchut, F., Thomas, N., Vilotte, J.-P. & Bristeau, M.-O. 2007 Numerical modeling of self-channeling granular flows and of their levee-channel deposits. J. Geophys. Res. 112, F02017.CrossRefGoogle Scholar
Mangeney-Castelnau, A., Bouchut, F., Vilotte, J.-P., Lajeunesse, E., Aubertin, A. & Pirulli, M. 2005 On the use of Saint-Venant equations to simulate the spreading of a granular mass. J. Geophys. Res. 110, B09103.CrossRefGoogle Scholar
Mangeney-Castelnau, A., Vilotte, J.-P., Bristeau, M.-O., Perthame, B., Bouchut, F., Simeoni, C. & Yerneni, S. 2003 Numerical modeling of avalanches based on Saint-Venant equations using a kinetic scheme. J. Geophys. Res. 108 (B11), 2527.CrossRefGoogle Scholar
Noble, P. & Vila, J.-P. 2013 Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations. J. Fluid Mech. 735, 29–60.CrossRefGoogle Scholar
Peruzzetto, M., Komorowski, J.-C., Le Friant, A., Rosas-Carbajal, M., Mangeney, A. & Legendre, Y. 2019 Modeling of partial dome collapse of La Soufrière of Guadeloupe volcano: implications for hazard assessment and monitoring. Sci. Rep. 9 (1), 13105.CrossRefGoogle ScholarPubMed
Pitman, E.B., Nichita, C.C., Patra, A., Bauer, A., Sheridan, M. & Bursik, M. 2003 Computing granular avalanches and landslides. Phys. Fluids 15 (12), 3638–3646.CrossRefGoogle Scholar
Pouliquen, O. 1999 Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11 (3), 542–548.CrossRefGoogle Scholar
Pouliquen, O., Cassar, C., Forterre, Y., Jop, P. & Nicolas, M. 2005 How do grains flow: towards a simple rheology for dense granular flows. Powders Grains 2005, 859–865.Google Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.CrossRefGoogle Scholar
Pouliquen, O. & Forterre, Y. 2009 A non-local rheology for dense granular flows. Phil. Trans. R. Soc. Lond. A: Math. Phys. Engng Sci. 367 (1909), 5091–5107.Google ScholarPubMed
Pudasaini, S.P. & Hutter, K. 2003 Rapid shear flows of dry granular masses down curved and twisted channels. J. Fluid Mech. 495, 193–208.CrossRefGoogle Scholar
Razis, D., Edwards, A.N., Gray, J.M.N.T. & van der Weele, K. 2014 Arrested coarsening of granular roll waves. Phys. Fluids 26, 123305.CrossRefGoogle Scholar
Richard, G.L., Couderc, F. & Vila, J.P. 2023 Reconstruction of the 3-D fields with a depth-averaged model for open-channel flows in the smooth turbulent case. J. Fluid Mech. 954, A24.CrossRefGoogle Scholar
Richard, G.L. 2024 Roll waves in a predictive model for open-channel flows in the smooth turbulent case. J. Fluid Mech. 983, A31.CrossRefGoogle Scholar
Richard, G.L. & Gavrilyuk, S.L. 2012 A new model of roll waves: comparison with Brock’s experiments. J. Fluid Mech. 698, 374–405.CrossRefGoogle Scholar
Richard, G.L., Gisclon, M., Ruyer-Quil, C. & Vila, J.-P. 2019 Optimization of consistent two-equation models for thin film flows. Eur. J. Mech. (B/Fluids) 76, 7–25.CrossRefGoogle Scholar
Richard, G.L., Ruyer-Quil, C. & Vila, J.-P. 2016 A three-equation model for thin films down an inclined plane. J. Fluid Mech. 804, 162–200.CrossRefGoogle Scholar
Rocha, F.M., Johnson, C.G. & Gray, J.M.N.T. 2019 Self-channelisation and levee formation in monodisperse granular flows. J. Fluid Mech. 876, 591–641.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B-Condens. Matt. Comp. Syst. 15 (2), 357–369.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2002 Further accuracy and convergence results on the modeling of flows down inclined planes by weighted-residual approximations. Phys. Fluids 14 (1), 170–183.CrossRefGoogle Scholar
Saingier, G., Deboeuf, S. & Lagrée, P.-Y. 2016 On the front shape of an inertial granular flow down a rough incline. Phys. Fluids 28, 053302.CrossRefGoogle Scholar
Savage, S.B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.CrossRefGoogle Scholar
Schaeffer, D.G., Barker, T., Tsuji, D., Gremaud, P., Shearer, M. & Gray, J.M.N.T. 2019 Constitutive relations for compressible granular flow in the inertial regime. J. Fluid Mech. 874, 926–951.CrossRefGoogle Scholar
Teshukov, V.M. 2007 Gas-dynamic analogy for vortex free-boundary flows. J. Appl. Mech. Tech. Phys. 48 (3), 303–309.CrossRefGoogle Scholar
Whitham, G.B. 1974 Linear and Nonlinear Waves. Wiley-Interscience.Google Scholar