Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-29T03:47:49.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic modelling of rarefied gas mixtures with disparate mass in strong non-equilibrium flows

Published online by Cambridge University Press:  05 December 2024

Qi Li Open the ORCID record for Qi Li [Opens in a new window] ,
Jianan Zeng  and
Lei Wu Open the ORCID record for Lei Wu [Opens in a new window]
Qi Li
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
Jianan Zeng
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
Lei Wu*
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

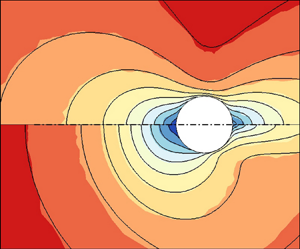
The simulation of rarefied gas flow based on the Boltzmann equation is challenging, especially when the gas mixtures have disparate molecular masses. In this paper, a computationally tractable kinetic model is proposed for monatomic gas mixtures, to mimic the Boltzmann collision operator as closely as possible. The intra- and inter-collisions are modelled separately using relaxation approximations, to correctly recover the relaxation time scales that could span several orders of magnitude. The proposed kinetic model preserves the accuracy of the Boltzmann equation in the continuum regime by recovering four critical transport properties of a gas mixture: the shear viscosity, the thermal conductivity, the coefficients of diffusion and the thermal diffusion. While in the rarefied flow regimes, the kinetic model is found to be accurate when comparing its solutions with those from the direct simulation Monte Carlo method in several representative cases (e.g. one-dimensional normal shock wave, Fourier flow and Couette flow, two-dimensional supersonic flow passing a cylinder and nozzle flow into a vacuum), for binary mixtures with a wide range of mass ratios, species concentrations and different intermolecular potentials. Pronounced separations in species properties have been observed, and the flow characteristics of gas mixtures in shock waves are found to change as the molecular mass ratio increases from 10 to 1000.

JFM classification

Rarefied Gas Flow: Rarefied Gas Flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A5
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Agrawal, S., Singh, S.K. & Ansumali, S. 2020 Fokker–Planck model for binary mixtures. J. Fluid Mech. 899, A25.CrossRefGoogle Scholar
Alves, L.L., Bogaerts, A., Guerra, V. & Turner, M.M. 2018 Foundations of modelling of nonequilibrium low-temperature plasmas. Plasma Sources Sci. Technol. 27 (2), 023002.CrossRefGoogle Scholar
Andries, P., Aoki, K. & Perthame, B. 2002 A consistent BGK-type model for gas mixtures. J. Stat. Phys. 106 (516), 993–1018.CrossRefGoogle Scholar
Andries, P., Le Tallec, P., Perlat, J. & Perthame, B. 2000 The Gaussian-BGK model of Boltzmann equation with small Prandtl number. Eur. J. Mech. (B/Fluids) 19 (6), 813–830.CrossRefGoogle Scholar
Bellan, P.M. 2006 Fundamentals of Plasma Physics. Cambridge University Press.CrossRefGoogle Scholar
Bhatnagar, P.L., Gross, E.P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525.CrossRefGoogle Scholar
Bich, E., Hellmann, R. & Vogel, E. 2007 Ab initio potential energy curve for the helium atom pair and thermophysical properties of the dilute helium gas. II. Thermophysical standard values for low-density helium. Mol. Phys. 105 (23-24), 3035–3049.CrossRefGoogle Scholar
Bird, G.A. 1968 The structure of normal shockwaves in a binary gas mixture. J. Fluid Mech. 31 (4), 657–668.CrossRefGoogle Scholar
Bird, G.A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Oxford University Press.CrossRefGoogle Scholar
Bisi, M., Boscheri, W., Dimarco, G., Groppi, M. & Martalò, G. 2022 A new mixed Boltzmann-BGK model for mixtures solved with an IMEX finite volume scheme on unstructured meshes. Appl. Maths Comput. 433, 127416.CrossRefGoogle Scholar
Bisi, M., Groppi, M. & Martalò, G. 2021 Macroscopic equations for inert gas mixtures in different hydrodynamic regimes. J. Phys. A: Math. Theor. 54 (8), 085201.CrossRefGoogle Scholar
Bisi, M., Monaco, R. & Soares, A.J. 2018 A BGK model for reactive mixtures of polyatomic gases with continuous internal energy. J. Phys. A: Math. Theor. 51 (12), 125501.CrossRefGoogle Scholar
Bisi, M. & Travaglini, R. 2020 A BGK model for mixtures of monoatomic and polyatomic gases with discrete internal energy. Phys. A: Stat. Mech. Appl. 547, 124441.CrossRefGoogle Scholar
Bobylev, A., Bisi, M., Groppi, M., Spiga, G. & Potapenko, I. 2018 A general consistent BGK model for gas mixtures. Kinet. Related Models 11 (6), 1377–1393.CrossRefGoogle Scholar
Boyd, D. 1996 Conservative species weighting scheme for the direct simulation Monte Carlo method. J. Thermophys. Heat Transfer 10, 579–585.CrossRefGoogle Scholar
Brull, S. 2015 An ellipsoidal statistical model for gas mixtures. Commun. Math. Sci. 13 (1), 1–13.CrossRefGoogle Scholar
Brull, S., Pavan, V. & Schneider, J. 2012 Derivation of a BGK model for mixtures. Eur. J. Mech. (B/Fluids) 33, 74–86.CrossRefGoogle Scholar
Brun, R. 2012 High Temperature Phenomena in Shock Waves. Springer.CrossRefGoogle Scholar
Chapman, S. 1958 Thermal diffusion in ionized gases. Proc. Phys. Soc. 72 (3), 353–362.CrossRefGoogle Scholar
Chapman, S. & Cowling, T.G. 1970 The Mathematical Theory of Non-Uniform Gases. Cambridge University Press.Google Scholar
Chen, S., Xu, K. & Cai, Q. 2015 A comparison and unification of ellipsoidal statistical and Shakhov BGK models. Adv. Appl. Maths Mech. 7 (2), 245–266.CrossRefGoogle Scholar
Erdman, P., Zipf, E., Hewlett, C., Loda, R., Collins, R.J., Levin, D.A. & Candler, G.V. 1993 Flight measurements of low velocity bow shock ultraviolet radiation. J. Thermophys. Heat Transfer 7 (1), 37–42.CrossRefGoogle Scholar
Farbar, E. & Boyd, D. 2010 Modeling of the plasma generated in a rarefied hypersonic shock layer. Phys. Fluid 22, 106101.CrossRefGoogle Scholar
Fei, F., Liu, H., Liu, Z. & Zhang, J. 2020 A benchmark study of kinetic models for shock waves. AIAA J. 58 (6), 2596–2608.CrossRefGoogle Scholar
Garzó, V., Santos, A. & Brey, J.J. 1989 A kinetic model for a multicomponent gas. Phys. Fluids A: Fluid Dyn. 1 (2), 380–383.CrossRefGoogle Scholar
Gmurczyk, A.S., Tarczynski, M. & Walenta, Z.A. 1979 Shock wave structure in the binary mixtures of gases with disparate molecular masses. In Proceedings of the 11th International Symposium on Rarefied Gas Dynamics, vol. 1, pp. 333–341. CEA.Google Scholar
Goldman, E. & Sirovich, L. 1969 The structure of shock-waves in gas mixtures. J. Fluid Mech. 35 (3), 575–597.CrossRefGoogle Scholar
Grad, H. 1960 Theory of rarefied gases. In Proceedings of the 1st International Symposium on Rarefied Gas Ddynamics, pp. 100–138. Pergamon.Google Scholar
Greene, J.M. 1973 Improved Bhatnagar–Gross–Krook model of electron-ion collisions. Phys. Fluids 16 (11), 2022–2023.CrossRefGoogle Scholar
Groppi, M., Monica, S. & Spiga, G. 2011 A kinetic ellipsoidal BGK model for a binary gas mixture. Europhys. Lett. 96 (6), 64002.CrossRefGoogle Scholar
Groppi, M. & Spiga, G. 2004 A Bhatnagar–Gross–Krook-type approach for chemically reacting gas mixtures. Phys. Fluids 16 (12), 4273–4284.CrossRefGoogle Scholar
Haack, J.R., Hauck, C.D. & Murillo, M.S. 2017 A conservative, entropic multispecies BGK model. J. Stat. Phys. 168 (4), 826–856.CrossRefGoogle Scholar
Hamel, B.B. 1965 Kinetic model for binary gas mixtures. Phys. Fluids 8 (3), 418–425.CrossRefGoogle Scholar
Hirschfelder, J.O., Curtiss, C.F. & Bird, R.B. 1954 Molecular Theory of Gases and Liquids. John Wiley & Sons.Google Scholar
Ho, M.T., Wu, L., Graur, I., Zhang, Y. & Reese, J.M. 2016 Comparative study of the Boltzmann and McCormack equations for Couette and Fourier flows of binary gaseous mixtures. Intl J. Heat Mass Transfer 96, 29–41.CrossRefGoogle Scholar
Holway, L.H. 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9, 1658–1673.CrossRefGoogle Scholar
Klingenberg, C., Pirner, M. & Puppo, G. 2017 A consistent kinetic model for a two-component mixture with an application to plasma. Kinet. Related Models 10 (2), 445–465.CrossRefGoogle Scholar
Kosuge, S. 2009 Model Boltzmann equation for gas mixtures: construction and numerical comparison. Eur. J. Mech. (B/Fluids) 28 (1), 170–184.CrossRefGoogle Scholar
Kosuge, S., Aoki, K. & Takata, S. 2001 Shock-wave structure for a binary gas mixture: finite-difference analysis of the Boltzmann equation for hard-sphere molecules. Eur. J. Mech. (B/Fluids) 20 (1), 87–126.CrossRefGoogle Scholar
Koura, K. & Matsumoto, H. 1991 Variable soft sphere molecular model for inverse-power-law or Lennard-Jones potential. Phys. Fluids A: Fluid Dyn. 3 (10), 2459–2465.CrossRefGoogle Scholar
Li, Q., Zeng, J., Huang, Z. & Wu, L. 2023 Kinetic modelling of rarefied gas flows with radiation. J. Fluid Mech. 965, A13.CrossRefGoogle Scholar
Li, Q., Zeng, J., Su, W. & Wu, L. 2021 Uncertainty quantification in rarefied dynamics of molecular gas: rate effect of thermal relaxation. J. Fluid Mech. 917, A58.CrossRefGoogle Scholar
Liu, C., Zhu, Y. & Xu, K. 2020 Unified gas-kinetic wave-particle methods I: continuum and rarefied gas flow. J. Comput. Phys. 401, 108977.CrossRefGoogle Scholar
Liu, W., Zhang, Y.B., Zeng, J.N. & Wu, L. 2024 Further acceleration of multiscale simulation of rarefied gas flow via a generalized boundary treatment. J. Comput. Phys. 503, 112830.CrossRefGoogle Scholar
Mathiaud, J., Mieussens, L. & Pfeiffer, M. 2022 An ES-BGK model for diatomic gases with correct relaxation rates for internal energies. Eur. J. Mech. (B/Fluids) 96, 65–77.CrossRefGoogle Scholar
McCormack, F.J. 1973 Construction of linearized kinetic models for gaseous mixtures and molecular gases. Phys. Fluids 16 (12), 2095–2105.CrossRefGoogle Scholar
Morse, T.F. 1964 Kinetic model equations for a gas mixture. Phys. Fluids 7 (12), 2012–2013.CrossRefGoogle Scholar
Nagnibeda, E. & Kustova, E. 2009 Non-Equilibrium Reacting Gas Flows: Kinetic Theory of Transport and Relaxation Processes. Springer.CrossRefGoogle Scholar
Park, W., Kim, S., Pfeiffer, M. & Jun, E. 2024 Evaluation of stochastic particle Bhatnagar–Gross–Krook methods with a focus on velocity distribution function. Phys. Fluids 36 (2), 027113.CrossRefGoogle Scholar
Pfeiffer, M., Garmirian, F. & Gorji, M.H. 2022 Exponential Bhatnagar-Gross-Krook integrator for multiscale particle-based kinetic simulations. Phys. Rev. E 106, 025303.CrossRefGoogle ScholarPubMed
Pfeiffer, M., Mirza, A. & Nizenkov, P. 2021 Multi-species modeling in the particle-based ellipsoidal statistical Bhatnagar–Gross–Krook method for monatomic gas species. Phys. Fluids 33 (3), 036106.CrossRefGoogle Scholar
Pirner, M. 2021 A review on BGK models for gas mixtures of mono and polyatomic molecules. Fluids 6 (11), 393.CrossRefGoogle Scholar
Plimpton, S.J., Moore, S.G., Borner, A., Stagg, A.K., Koehler, T.P., Torczynski, J.R. & Gallis, M.A. 2019 Direct simulation Monte Carlo on petaflop supercomputers and beyond. Phys. Fluids 31 (8), 086101.CrossRefGoogle Scholar
Raines, A. 2002 Study of a shock wave structure in gas mixtures on the basis of the Boltzmann equation. Eur. J. Mech. (B/Fluids) 21, 599–610.CrossRefGoogle Scholar
Ruyev, G.A., Fedorov, A.V. & Fomin, V.M. 2002 Special features of the shock-wave structure in mixtures of gases with disparate molecular masses. J. Appl. Mech. Tech. Phys. 43 (4), 529–537.CrossRefGoogle Scholar
Sawant, N., Dorschner, B. & Karlin, I.V. 2020 Consistent lattice Boltzmann model for multicomponent mixtures. J. Fluid Mech. 909, A1.CrossRefGoogle Scholar
Schmidt, B., Seiler, F. & Wörner, M. 1984 Shock structure near a wall in pure inert gas and in binary inert-gas mixtures. J. Fluid Mech. 143, 305–326.CrossRefGoogle Scholar
Shakhov, E.M. 1968 a Approximate kinetic equations in rarefied gas theory. Fluid Dyn. 3, 112–115.CrossRefGoogle Scholar
Shakhov, E.M. 1968 b Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 3 (5), 95–96.CrossRefGoogle Scholar
Sharipov, F. 2024 Ab initio modelling of transport phenomena in multi-component mixtures of rarefied gases. Intl J. Heat Mass Transfer 220, 124906.CrossRefGoogle Scholar
Sharipov, F. & Benites, V.J. 2015 Transport coefficients of helium-argon mixture based on ab initio potential. J. Chem. Phys. 143, 154104.CrossRefGoogle ScholarPubMed
Sharipov, F. & Dias, F.C. 2018 Structure of planar shock waves in gaseous mixtures based on ab initio direct simulation. Eur. J. Mech. (B/Fluids) 72, 251–263.CrossRefGoogle Scholar
Stephani, K.A., Goldstein, D.B. & Varghese, P.L. 2012 Consistent treatment of transport properties for five-species air direct simulation Monte Carlo/Navier–Stokes applications. Phys. Fluids 24 (7), 077101.CrossRefGoogle Scholar
Strapasson, J.L. & Sharipov, F. 2014 Ab initio simulation of heat transfer through a mixture of rarefied gases. Intl J. Heat Mass Transfer 71, 91–97.CrossRefGoogle Scholar
Su, W., Zhu, L., Wang, P., Zhang, Y. & Wu, L. 2020 a Can we find steady-state solutions to multiscale rarefied gas flows within dozens of iterations? J. Comput. Phys. 407, 109245.CrossRefGoogle Scholar
Su, W., Zhu, L.H. & Wu, L. 2020 b Fast convergence and asymptotic preserving of the general synthetic iterative scheme. SIAM J. Sci. Comput. 42 (6), B1517–B1540.CrossRefGoogle Scholar
Takata, S., Sugimoto, H. & Kosuge, S. 2007 Gas separation by means of the Knudsen compressor. Eur. J. Mech. (B/Fluids) 26 (2), 155–181.CrossRefGoogle Scholar
Tantos, C. & Valougeorgis, D. 2018 Conductive heat transfer in rarefied binary gas mixtures confined between parallel plates based on kinetic modeling. Intl J. Heat Mass Transfer 117, 846–860.CrossRefGoogle Scholar
Tantos, C., Varoutis, S. & Day, C. 2021 Heat transfer in binary polyatomic gas mixtures over the whole range of the gas rarefaction based on kinetic deterministic modeling. Phys. Fluids 33 (2), 022004.CrossRefGoogle Scholar
Tantos, C., Waroutis, S., Hauer, V., Day, C. & Innocente, P. 2024 3D numerical study of netural gas dynamics in the DTT particle exhaust using the DSMC method. Nucl. Fusion 64, 016019.CrossRefGoogle Scholar
Teng, S., Hao, M., Liu, J.X., Bian, X., Xie, Y.H. & Liu, K. 2023 Pollutant inhibition in an extreme ultraviolet lighography machine by dynamic gas lock. J. Clean. Prod. 430, 139664.CrossRefGoogle Scholar
Tipton, E.L., Tompson, R.V. & Loyalka, S.K. 2009 a Chapman–Enskog solutions to arbitrary order in Sonine polynomials II: viscosity in a binary, rigid-sphere, gas mixture. Eur. J. Mech. (B/Fluids) 28 (3), 335–352.CrossRefGoogle Scholar
Tipton, E.L., Tompson, R.V. & Loyalka, S.K. 2009 b Chapman–Enskog solutions to arbitrary order in Sonine polynomials III: diffusion, thermal diffusion, and thermal conductivity in a binary, rigid-sphere, gas mixture. Eur. J. Mech. (B/Fluids) 28 (3), 353–386.CrossRefGoogle Scholar
Todorova, B.N. & Steijl, R. 2019 Derivation and numerical comparison of Shakhov and ellipsoidal statistical kinetic models for a monoatomic gas mixture. Eur. J. Mech. (B/Fluids) 76, 390–402.CrossRefGoogle Scholar
Todorova, B.N., White, C. & Steijl, R. 2020 Modeling of nitrogen and oxygen gas mixture with a novel diatomic kinetic model. AIP Adv. 10 (9), 095218.CrossRefGoogle Scholar
Vogel, E., Jager, B., Hellmann, R. & Bich, E. 2010 Ab initio pair potential energy curve for the argon atom pair and thermophysical properties for the dilute argon gas. II. Thermophysical properties for low-density argon. Mol. Phys. 108 (24), 3335–3352.CrossRefGoogle Scholar
Wagner, W. 1992 A convergence proof for Bird's direct simulation Monte Carlo method for the Boltzmann equation. J. Stat. Phys. 66, 1011–1044.CrossRefGoogle Scholar
Wilke, C.R. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18 (4), 517–519.CrossRefGoogle Scholar
Wu, L., White, C., Scanlon, T.J., Reese, J.M. & Zhang, Y.H. 2015 a A kinetic model of the Boltzmann equation for non-vibrating polyatomic gases. J. Fluid Mech. 763, 24–50.CrossRefGoogle Scholar
Wu, L., Zhang, J., Reese, J.M. & Zhang, Y. 2015 b A fast spectral method for the Boltzmann equation for monatomic gas mixtures. J. Comput. Phys. 298, 602–621.CrossRefGoogle Scholar
Wu, L., Zhang, Y. & Reese, J.M. 2015 c Fast spectral solution of the generalized Enskog equation for dense gases. J. Comput. Phys. 303, 66–79.CrossRefGoogle Scholar
Yuan, R.F. & Wu, L. 2022 Capturing the influence of intermolecular potential in rarefied gas flows by a kinetic model with velocity-dependent collision frequency. J. Fluid Mech. 942, A13.CrossRefGoogle Scholar
Zeng, J., Li, Q. & Wu, L. 2022 Kinetic modeling of rarefied molecular gas dynamics (in Chinese). Acta Aerodyn. Sin. 40 (2), 1–30.Google Scholar
Zeng, J., Li, Q. & Wu, L. 2024 General synthetic iterative scheme for rarefied gas mixture flows. J. Comput. Phys. 519 (1), 113420.CrossRefGoogle Scholar
Zeng, J., Su, W. & Wu, L. 2023 a General synthetic iterative scheme for unsteady rarefied gas flows. Commun. Comput. Phys. 34 (1), 173–207.CrossRefGoogle Scholar
Zeng, J., Yuan, R., Zhang, Y., Li, Q. & Wu, L. 2023 b General synthetic iterative scheme for polyatomic rarefied gas flows. Comput. Fluids 265, 105998.CrossRefGoogle Scholar