Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-28T09:59:53.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong convergence of peaks over a threshold

Part of: Stochastic processes Limit theorems Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  23 August 2023

Simone A. Padoan  and
Stefano Rizzelli
Simone A. Padoan*
Affiliation:
Bocconi University
Stefano Rizzelli*
Affiliation:
Catholic University
*
*Postal address: Department of Decision Sciences, via Roentgen 1, 20136, Milan, Italy. Email: [email protected]
**Postal address: Department of Statistical Science, via Lanzone 18, 20123, Milan, Italy. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Extreme value theory plays an important role in providing approximation results for the extremes of a sequence of independent random variables when their distribution is unknown. An important one is given by the generalised Pareto distribution 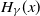$H_\gamma(x)$ as an approximation of the distribution 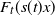$F_t(s(t)x)$ of the excesses over a threshold t, where s(t) is a suitable norming function. We study the rate of convergence of 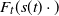$F_t(s(t)\cdot)$ to 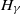$H_\gamma$ in variational and Hellinger distances and translate it into that regarding the Kullback–Leibler divergence between the respective densities.

Keywords

Convergence rateexceedancesextreme quantilegeneralised Paretotail index

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60F15: Strong theorems 60B10: Convergence of probability measures
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 2 , June 2024 , pp. 529 - 539
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Balkema, A. A. and de Haan, L. (1974). Residual life time at great age. Ann. Prob. 2, 792–804.CrossRefGoogle Scholar
Bobbia, B., Dombry, C. and Varron, D. (2021). The coupling method in extreme value theory. Bernoulli 27, 1824–1850.CrossRefGoogle Scholar
Bücher, B. and Zhou, C. (2021). A horse race between the block maxima method and the peak-over-threshold approach. Statist. Sci. 36, 360–378.CrossRefGoogle Scholar
de Haan, L. and Ferreira, A. (2006). Extreme Value Theory: An Introduction. Springer, New York.CrossRefGoogle Scholar
Dey, D. K. and Yan, J. (2016). Extreme Value Modeling and Risk Analysis: Methods and Applications. CRC Press, New York.CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (2013). Modelling Extremal Events: For Insurance and Finance. Springer, Berlin.Google Scholar
Falk, M., Hüsler, J. and Reiss, R.-D. (2010). Laws of Small Numbers: Extremes and Rare Events. Birkhäuser, Basel.Google Scholar
Ghosal, S., Ghosh, J. K. and van der Vaart, A. W. (2000). Convergence rates of posterior distributions. Ann. Statist. 28, 500–531.CrossRefGoogle Scholar
Ghosal, S. and van der Vaart, A. W. (2017). Fundamentals of Nonparametric Bayesian Inference. Cambridge University Press.CrossRefGoogle Scholar
Kulik, R. and Soulier, P. (2020). Heavy-Tailed Time Series. Springer, New York.CrossRefGoogle Scholar
Pickands, III, J. (1975). Statistical inference using extreme order statistics. Ann. Statist. 3, 119–131.Google Scholar
Raoult, J.-P. and Worms, R. (2003). Rate of convergence for the generalized Pareto approximation of the excesses. Adv. Appl. Prob. 35, 1007–1027.CrossRefGoogle Scholar
Resnick, S. I. (2007). Extreme Values, Regular Variation, and Point Processes. Springer, New York.Google Scholar
Supplementary material: PDF

Padoan and Rizzelli supplementary material

Padoan and Rizzelli supplementary material

Download Padoan and Rizzelli supplementary material(PDF)
PDF 299.6 KB