Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-27T06:20:56.016Z Has data issue: false hasContentIssue false
  • English
  • Français

On a wider class of prior distributions for graphical models

Part of: Graph theory

Published online by Cambridge University Press:  08 June 2023

Abhinav Natarajan ,
Willem van den Boom Open the ORCID record for Willem van den Boom [Opens in a new window] ,
Kristoforus Bryant Odang  and
Maria de Iorio
Abhinav Natarajan*
Affiliation:
University of Oxford
Willem van den Boom*
Affiliation:
National University of Singapore
Kristoforus Bryant Odang*
Affiliation:
National University of Singapore
Maria de Iorio*
Affiliation:
National University of Singapore; Singapore Institute for Clinical Sciences, A*STAR; University College London
*
*Postal address: Mathematical Institute, University of Oxford, Wellington Square, Oxford OX1 2JD, UK. Email address: [email protected]
**Postal address: Yong Loo Lin School of Medicine, National University of Singapore, 10 Medical Dr, Singapore 117597.
**Postal address: Yong Loo Lin School of Medicine, National University of Singapore, 10 Medical Dr, Singapore 117597.
*****Postal address: Yong Loo Lin School of Medicine, National University of Singapore, 10 Medical Dr, Singapore 117597. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Gaussian graphical models are useful tools for conditional independence structure inference of multivariate random variables. Unfortunately, Bayesian inference of latent graph structures is challenging due to exponential growth of 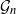$\mathcal{G}_n$, the set of all graphs in n vertices. One approach that has been proposed to tackle this problem is to limit search to subsets of 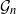$\mathcal{G}_n$. In this paper we study subsets that are vector subspaces with the cycle space 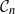$\mathcal{C}_n$ as the main example. We propose a novel prior on 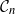$\mathcal{C}_n$ based on linear combinations of cycle basis elements and present its theoretical properties. Using this prior, we implement a Markov chain Monte Carlo algorithm, and show that (i) posterior edge inclusion estimates computed with our technique are comparable to estimates from the standard technique despite searching a smaller graph space, and (ii) the vector space perspective enables straightforward implementation of MCMC algorithms.

Keywords

Gaussian graphical modelBayesian statisticsnetwork inferencecycle spaceMarkov chain Monte Carlovector space

MSC classification

Secondary: 05C80: Random graphs 05C90: Applications
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 1 , March 2024 , pp. 230 - 243
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aldous, D. J. (1990). The random walk construction of uniform spanning trees and uniform labelled trees. SIAM J. Discrete Math. 3, 450–465.CrossRefGoogle Scholar
Armstrong, H., Carter, C. K., Wong, K. F. K. and Kohn, R. (2009). Bayesian covariance matrix estimation using a mixture of decomposable graphical models. Statist. Comput. 19, 303–316.CrossRefGoogle Scholar
Atay-Kayis, A. and Massam, H. (2005). A Monte Carlo method for computing the marginal likelihood in nondecomposable Gaussian graphical models. Biometrika 92, 317–335.CrossRefGoogle Scholar
Axler, S. (2015). Linear Algebra Done Right, 3rd edn (Undergraduate Texts in Mathematics). Springer, Cham and Heidelberg.Google Scholar
Bender, E., Richmond, L. and Wormald, N. (1985). Almost all chordal graphs split. J. Austral. Math. Soc. 38, 214–221.CrossRefGoogle Scholar
Cayley, A. (1889). A theorem on trees. Quart. J. Pure Appl. Math. 23, 376–378.Google Scholar
Chaiken, S. and Kleitman, D. J. (1978). Matrix tree theorems. J. Combinatorial Theory A 24, 377–381.CrossRefGoogle Scholar
Chung, F. R. and Mumford, D. (1994). Chordal completions of planar graphs. J. Combinatorial Theory B 62, 96–106.CrossRefGoogle Scholar
Dawid, A. P. and Lauritzen, S. L. (1993). Hyper Markov laws in the statistical analysis of decomposable graphical models. Ann. Statist. 21, 1272–1317.CrossRefGoogle Scholar
Dempster, A. P. (1972). Covariance selection. Biometrics 28, 157–175.CrossRefGoogle Scholar
Dethlefsen, C. and Højsgaard, S. (2005). A common platform for graphical models in R: the gRbase package. J. Statist. Softw. 14, 1–12.CrossRefGoogle Scholar
Dobra, A. and Lenkoski, A. (2011). Copula Gaussian graphical models and their application to modeling functional disability data. Ann. Appl. Statist. 5, 969–993.CrossRefGoogle Scholar
Duan, L. L. and Dunson, D. B. (2021). Bayesian spanning tree: estimating the backbone of the dependence graph. Available at arXiv:2106.16120v1.Google Scholar
Giudici, P. (1996). Learning in graphical Gaussian models. In Bayesian Statistics 5, ed. J. M. Bernardo et al., pp. 621–628. Oxford University Press.Google Scholar
Giudici, P. and Green, P. J. (1999). Decomposable graphical Gaussian model determination. Biometrika 86, 785–801.CrossRefGoogle Scholar
Green, P. J. and Thomas, A. (2013). Sampling decomposable graphs using a Markov chain on junction trees. Biometrika 100, 91–110.CrossRefGoogle Scholar
Højsgaard, S., Edwards, D. and Lauritzen, S. (2012). Graphical Models with R. Springer, New York.CrossRefGoogle Scholar
Jones, B., Carvalho, C., Dobra, A., Hans, C., Carter, C. and West, M. (2005). Experiments in stochastic computation for high-dimensional graphical models. Statist. Sci. 20, 388–400.CrossRefGoogle Scholar
Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Amer. Math. Soc. 7, 48–50.CrossRefGoogle Scholar
Lauritzen, S. L. (1996). Graphical Models (Oxford Statistical Science Series). The Clarendon Press, Oxford University Press, New York.CrossRefGoogle Scholar
Lenkoski, A. and Dobra, A. (2011). Computational aspects related to inference in Gaussian graphical models with the G-Wishart prior. J. Comput. Graph. Statist. 20, 140–157.CrossRefGoogle Scholar
Lu, D., De Iorio, M., Jasra, A. and Rosner, G. L. (2020). Bayesian inference for latent chain graphs. Found. Data Sci. 2, 35–54.CrossRefGoogle Scholar
Miller, L. D., Smeds, J., George, J., Vega, V. B., Vergara, L., Ploner, A., Pawitan, Y., Hall, P., Klaar, S., Liu, E. T. and Bergh, J. (2005). An expression signature for p53 status in human breast cancer predicts mutation status, transcriptional effects, and patient survival. Proc. Nat. Acad. Sci. USA 102, 13550–13555.CrossRefGoogle Scholar
Mohammadi, R. and Wit, E. C. (2019). BDgraph: an R package for Bayesian structure learning in graphical models. J. Statist. Softw. 89, 1–30.CrossRefGoogle Scholar
Murray, I., Ghahramani, Z. and MacKay, D. J. C. (2006). MCMC for doubly-intractable distributions. In Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence (UAI’06), pp. 359–366. AUAI Press, Arlington, VA.Google Scholar
Niu, Y., Pati, D. and Mallick, B. K. (2021). Bayesian graph selection consistency under model misspecification. Bernoulli 27, 637–672.CrossRefGoogle ScholarPubMed
Peterson, C., Stingo, F. C. and Vannucci, M. (2015). Bayesian inference of multiple Gaussian graphical models. J. Amer. Statist. Assoc. 110, 159–174.CrossRefGoogle ScholarPubMed
Roverato, A. (2002). Hyper inverse Wishart distribution for non-decomposable graphs and its application to Bayesian inference for Gaussian graphical models. Scand. J. Statist. 29, 391–411.CrossRefGoogle Scholar
Schild, A.. (2018). An almost-linear time algorithm for uniform random spanning tree generation. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2018), pp. 214–227.CrossRefGoogle Scholar
Schwaller, L., Robin, S. and Stumpf, M. (2019). Closed-form Bayesian inference of graphical model structures by averaging over trees. J. Soc. Française Statist. 160, 1–23.Google Scholar
Scott, J. G. and Carvalho, C. M. (2008). Feature-inclusion stochastic search for Gaussian graphical models. J. Comput. Graph. Statist. 17, 790–808.CrossRefGoogle Scholar
Sonntag, D. and Peña, J. M. (2015). Chain graphs and gene networks. In Foundations of Biomedical Knowledge Representation (Lecture Notes Comput. Sci. 9521), ed. A. Hommersom and P. Lucas, pp. 159–178. Springer, Cham.Google Scholar
Stingo, F. and Marchetti, G. M. (2015). Efficient local updates for undirected graphical models. Statist. Comput. 25, 159–171.CrossRefGoogle Scholar
Tan, L. S., Jasra, A., De Iorio, M. and Ebbels, T. M. (2017). Bayesian inference for multiple Gaussian graphical models with application to metabolic association networks. Ann. Appl. Statist. 11, 2222–2251.CrossRefGoogle Scholar
Uhler, C., Lenkoski, A. and Richards, D. (2018). Exact formulas for the normalizing constants of Wishart distributions for graphical models. Ann. Statist. 46, 90–118.CrossRefGoogle Scholar
Van den Boom, W., Jasra, A., De Iorio, M., Beskos, A. and Eriksson, J. G. (2022). Unbiased approximation of posteriors via coupled particle Markov chain Monte Carlo. Statist. Comput. 32, 36.CrossRefGoogle Scholar
Veblen, O. (1912). An application of modular equations in analysis situs. Ann. of Math. 14, 86–94.CrossRefGoogle Scholar
Wallis, W. D. (2010). A Beginner’s Guide to Graph Theory. Springer, New York.Google Scholar
Wang, H. and Carvalho, C. M. (2010). Simulation of hyper-inverse Wishart distributions for non-decomposable graphs. Electron. J. Statist. 4, 1470–1475.CrossRefGoogle Scholar
Wang, H. and Li, S. Z. (2012). Efficient Gaussian graphical model determination under G-Wishart prior distributions. Electron. J. Statist. 6, 168–198.CrossRefGoogle Scholar
Supplementary material: PDF

Natarajan et al. supplementary material

Natarajan et al. supplementary material

Download Natarajan et al. supplementary material(PDF)
PDF 523.2 KB