Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-05-04T20:15:26.476Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ASYMPTOTIC FORMULA IN WARING'S PROBLEM: ONE SQUARE AND THREE FIFTH POWERS

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  18 December 2014

JÖRG BRÜDERN
JÖRG BRÜDERN*
Affiliation:
Mathematisches Institut, Bunsenstrasse 3–5, D-37073 Göttingen, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Let r(n) denote the number of representations of the natural number n as the sum of one square and three fifth powers of positive integers. A formal use of the circle method predicts the asymptotic relation(1)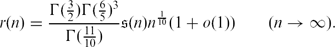

$\begin{equation*}r(n) = \frac{\Gamma(\frac32)\Gamma(\frac65)^3}{\Gamma(\frac{11}{10})} {\mathfrak s}(n) {n}^\frac1{10} (1 + o(1)) \qquad (n\to\infty).\end{equation*}$
Here ${\mathfrak s}$(n) is the singular series associated with sums of a square and three fifth powers, see (13) below for a precise definition. The main purpose of this note is to confirm (1) in mean square.

MSC classification

Primary: 11P55: Applications of the Hardy-Littlewood method
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 3 , September 2015 , pp. 681 - 692
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Brüdern, J., Sums of squares and higher powers. I. J. London Math. Soc. (2) 35 (2) (1987), 233–243.CrossRefGoogle Scholar
2.Brüdern, J., A problem in additive number theory, Math. Proc. Cambridge Philos. Soc. 103 (1) (1988), 27–33.CrossRefGoogle Scholar
3.Brüdern, J. and Kawada, K., The asymptotic formula in Waring's problem for one square and seventeen fifth powers, Monatsh. Math. 162 (4) (2011), 385–407.CrossRefGoogle Scholar
4.Davenport, H. and Heilbronn, H., On Waring's problem: two cubes and one square, Proc. London Math. Soc. (2) 43 (1) (1937), 73–104.Google Scholar
5.Friedlander, J.B. and Wooley, T.D., On Waring's problem: Two squares and three biquadrates, Mathematika 60 (1) (2014), 153–165.CrossRefGoogle Scholar
6.Hardy, G.H. and Wright, E.M., An introduction to the theory of numbers, 5th ed. (The Clarendon Press, Oxford University Press, New York, 1979).Google Scholar
7.Hooley, C., On the representations of a number as the sum of two cubes, Math. Z. 82 (1963), 259–266.CrossRefGoogle Scholar
8.Hooley, C., On a new approach to various problems of Waring's type, Recent progress in analytic number theory, vol. 1 (Durham, 1979) (Academic Press, London-New York, 1981), 127–191.Google Scholar
9.Hooley, C., On Waring's problem for two squares and three cubes Quart. J. Math. Oxford Ser. (2) 16 (1965), 289–296.Google Scholar
10.Sinnadurai, J. St.-C. L., Representation of integers as sums of six cubes and one square, Quart. J. Math. Oxford Ser. 16 (2) (1965), 289–296.CrossRefGoogle Scholar
11.Stanley, G.K., The representation of a number as the sum of one square and a number of k-th powers, Proc. London Math. Soc. (2) 31 (1) (1930), 512–553.CrossRefGoogle Scholar
12.Vaughan, R.C., On the representation of numbers as sums of squares, cubes and fourth powers, PhD Thesis (London, 1969).Google Scholar
13.Vaughan, R.C., A ternary additive problem, Proc. London Math. Soc. (3) 41 (3) (1980), 516–532.CrossRefGoogle Scholar
14.Vaughan, R.C., On Waring's problem: One square and five cubes, Quart. J. Math. Oxford Ser. (2) 37 (145) (1986), 117–127.CrossRefGoogle Scholar
15.Vaughan, R.C., On Waring's problem for smaller exponents. II, Mathematika 33 (1) (1986), 6–22.CrossRefGoogle Scholar
16.Vaughan, R.C., The Hardy-Littlewood method, 2nd ed. Cambridge Tracts in Mathematics, vol. 125 (Cambridge University Press, Cambridge, 1997).CrossRefGoogle Scholar
17.Vaughan, R.C., On generating functions in additive number theory. I, Analytic number theory (Cambridge University Press, Cambridge, 2009), 436–448.Google Scholar
18.Wooley, T.D., On Waring's problem: Some consequences of Golubeva's method, J. Lond. Math. Soc. (2) 88 (3) (2013), 699–715.CrossRefGoogle Scholar