Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-05-02T06:42:45.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Dehn functions of mapping tori of right-angled Artin groups

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  11 January 2024

Kristen Pueschel Open the ORCID record for Kristen Pueschel [Opens in a new window]  and
Timothy Riley
Kristen Pueschel*
Affiliation:
Penn State New Kensington, New Kensington, PA, USA
Timothy Riley
Affiliation:
Cornell University, Ithaca, NY, USA
*
Corresponding author: Kristen Pueschel; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

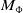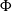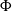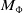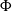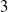The algebraic mapping torus $M_{\Phi }$ of a group $G$ with an automorphism $\Phi$ is the HNN-extension of $G$ in which conjugation by the stable letter performs $\Phi$. We classify the Dehn functions of $M_{\Phi }$ in terms of $\Phi$ for a number of right-angled Artin groups (RAAGs) $G$, including all $3$-generator RAAGs and 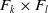$F_k \times F_l$ for all 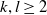$k,l \geq 2$.

Keywords

Dehn functionright-angled Artin groupmapping torus

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F36: Braid groups; Artin groups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 66 , Issue 2 , May 2024 , pp. 252 - 289
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alonso, J. M., Inégalités isopérimétriques et quasi-isométries, C. R. Acad. Sci. Paris Sér. I Math. 311(12) (1990), 761–764.Google Scholar
Bestvina, M., Feighn, M. and Handel, M., The Tits alternative for ${\rm Out}(F_n)$ . I. Dynamics of exponentially-growing automorphisms, Ann. Math. (2) 151(2) (2000), 517–623.CrossRefGoogle Scholar
Bestvina, M. and Handel, M., Train tracks and automorphisms of free groups, Ann. Math. (2) 135(1) (1992), 135–151.CrossRefGoogle Scholar
Bogopolski, O., Martino, A. and Ventura, E., The automorphism group of a free-by-cyclic group in rank 2, Commun. Algebra 35(5) (2007), 1675–1690.CrossRefGoogle Scholar
Bowditch, B. H., Relatively hyperbolic groups, Int. J. Algebra Comput. 22(3) (2012), 1250016,66.CrossRefGoogle Scholar
Brady, N. and Soroko, I., Dehn functions of subgroups of right-angled Artin groups, Geom. Dedicata 200 (2019), 197–239.CrossRefGoogle Scholar
Bridson, M. R. and Gersten, S. M., The optimal isoperimetric inequality for torus bundles over the circle, Q. J. Math. Oxford Ser. 2(185) (1996), 47–23.Google Scholar
Bridson, M. R. and Groves, D., The quadratic isoperimetric inequality for mapping tori of free group automorphisms, Mem. Am. Math. Soc. 203(955) (2010), xii+152.Google Scholar
Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 319 (Springer, Berlin, 1999).CrossRefGoogle Scholar
Bridson, M. R. and Pittet, C., Isoperimetric inequalities for the fundamental groups of torus bundles over the circle, Geom. Dedicata 49(2) (1994), 203–219.CrossRefGoogle Scholar
Brinkmann, P., Hyperbolic automorphisms of free groups, Geom. Funct. Anal. 10(5) (2000), 1071–1089.CrossRefGoogle Scholar
Button, J. O. and Kropholler, R. P., Nonhyperbolic free-by-cyclic and one-relator groups, N. Y. J. Math. 22 (2016), 755–774.Google Scholar
Diestel, R., Graph theory, Graduate Texts in Mathematics, vol. 173, 3rd edition (Springer, Berlin, 2005).Google Scholar
Farb, B., Relatively hyperbolic groups, Geom. Funct. Anal. 8(5) (1998), 810–840.CrossRefGoogle Scholar
Gersten, S. M., Isoperimetric and isodiametric functions of finite presentations, in Geometric group theory, Vol. 1 (Sussex, 1991), London Math. Soc. Lecture Note Ser., vol. 181 (Cambridge University Press, Cambridge, 1993), 79–96.CrossRefGoogle Scholar
Gersten, S. M. and Riley, T. R., Some duality conjectures for finite graphs and their group theoretic consequences, Proc. Edinb. Math. Soc. 2(2) (2005), 48–421.Google Scholar
Hermiller, S. and Meier, J., Algorithms and geometry for graph products of groups, J. Algebra 171(1) (1995), 230–257.CrossRefGoogle Scholar
Laurence, M. R., A generating set for the automorphism group of a graph group, J. London Math. Soc. (2) 52(2) (1995), 318–334.CrossRefGoogle Scholar
Levitt, G., Counting growth types of automorphisms of free groups, Geom. Funct. Anal. 19(4) (2009), 1119–1146.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial group theory, Classics in Mathematics (Springer, Berlin, 2001), Reprint of the 1977 edition.CrossRefGoogle Scholar
Osin, D. V., Relatively hyperbolic groups: intrinsic geometry, algebraic properties, and algorithmic problems, Mem. Am. Math. Soc. 179(843) (2006), vi+100.Google Scholar
Papasoglu, P., On the asymptotic cone of groups satisfying a quadratic isoperimetric inequality, J. Differ. Geom. 44(4) (1996), 789–806.CrossRefGoogle Scholar
Piggott, A., Detecting the growth of free group automorphisms by their action on the homology of subgroups of finite index. Available at https://arxiv.org/abs/math/0409319v1 Google Scholar
Servatius, H., Automorphisms of graph groups, J. Algebra 126(1) (1989), 34–60.CrossRefGoogle Scholar
VanWyk, L., Graph groups are biautomatic, J. Pure Appl. Algebra 94(3) (1994), 341–352.CrossRefGoogle Scholar