Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-27T13:47:13.144Z Has data issue: false hasContentIssue false
  • English
  • Français

An analogue of a conjecture of Sato and Tate for a Hilbert modular form

Published online by Cambridge University Press:  18 May 2009

H. L. Resnikoff  and
R. L. Saldaña
H. L. Resnikoff
Affiliation:
Rice University, Houston, Texas 77001, U.S.A.
R. L. Saldaña
Affiliation:
Rice University, Houston, Texas 77001, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If k denotes a number field and εm is the product of an elliptic curve ε with itself m times over k, then for each prime π where ε has non-degenerate reduction, the zeta factor ζ(επ'S) can be expressed as

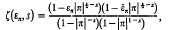
Where |π| denotes the norm of π. It is a consequence of a conjecture of Tate [16] that if ε does not have complex multiplications, then the numbers 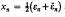are distributed according to the density function

that is, the density of the set of primes π such that – 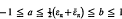is

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 16 , Issue 2 , September 1975 , pp. 69 - 87
Copyright
Copyright © Glasgow Mathematical Journal Trust 1975

References

REFERENCES

1.Braun, H. and Koecher, M., Jordan-Algebren, Springer, Berlin, 1966.CrossRefGoogle Scholar
2.Deligne, P., Formes modulaires et représentations l-adiques, Sém. Bourbaki 21 (1968/1969), No. 355.Google Scholar
3.Deligne, P., La conjecture de Weil. I, Pubt. Math. IHES No. 43, to appear.CrossRefGoogle Scholar
4.Gundlach, K.-B., Die Bestimmung der Funktionen zur Hilbertschen Modulgruppe des Zahlkörpers ℚ(√5), Math. Ann. 152 (1963), 226–256.CrossRefGoogle Scholar
5.Gundlach, K.-B., Die Bestimmung der Funktionen zu einigen Hilbertschen Modulgruppen, J. für die reine undangew. Math. 220 (1965), 109–153.Google Scholar
6.Hammond, W. F., The modular groups of Hilbert and Siegel, Amer. J. Math. 88 (1966), 497–516.CrossRefGoogle Scholar
7.Hermann, O., Über Hilbertsche Modulfunktionen und die Dirichletschen Reihen mit Eulerscher Produktentwicklung, Math. Ann. 127 (1954), p 357–400.CrossRefGoogle Scholar
8.Koecher, M., An Elementary Approach to Bounded Symmetric Domains (Rice University, Houston, 1969).Google Scholar
9.Lehmer, D. H., Note on the distribution of Ramanujan's tau function, Math. Computation 24 (1970), 741–743.Google Scholar
10.Ramanujan, S., On certain arithmetical functions, Trans. Cambridge Phil. Soc. 22 (1916), 159–184.Google Scholar
11.Resnikoff, H. L., On the graded ring of Hilbert modular forms associated with ℚ(√5), Math. Ann. 208 (1974). 161–170.CrossRefGoogle Scholar
12.Resnikoff, H. L. and Saldaña, R. L., Some properties of Fourier coefficients of Eisenstein series of degree two, J. für die reine undangew. Math. 265 (1974), 90–109.Google Scholar
13.Serre, J.-P., Une interprétation des congruences relatives à la fonction τ de Ramanujan, Sém. Delange-Pisot-Poitou 9 (1967/1968), No. 14.Google Scholar
14.Serre, J.-P., Abelian l-adic Representations and Elliptic Curves (W. A. Benjamin, New York, 1968).Google Scholar
15.Serre, J.-P., Congruences et formes modulaires, Sém. Bourbaki 24 (1971/1972), No. 416.Google Scholar
16.Tate, J. T., Algebraic cycles and poles of zeta functions, in Arithmetical Algebraic Geometry (Harper and Row, New York, 1965).Google Scholar