Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-26T00:32:48.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Improvement of some discrete Hardy inequalities with variants

Part of: Inequalities

Published online by Cambridge University Press:  25 November 2024

Bikram Das ,
S. K. Chakraborty ,
Rudrajit Sadhu  and
Atanu Manna
Bikram Das
Affiliation:
Dr. APJ Abdul Kalam Technical University, Lucknow, Uttar Pradesh, India Indian Institute of Carpet Technology, Bhadohi, Uttar Pradesh, India
S. K. Chakraborty
Affiliation:
Ramkrishna Mission Vidyamandira, Howrah, West Bengal, India
Rudrajit Sadhu
Affiliation:
Sreegopal Banerjee College, Hooghly, West Bengal, India
Atanu Manna*
Affiliation:
Indian Institute of Carpet Technology, Bhadohi, Uttar Pradesh, India
*
Corresponding author: Atanu Manna; Emails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish a new version of one-dimensional discrete improved Hardy’s inequality with shifts by introducing a shifting discrete Dirichlet’s Laplacian. We prove that the general discrete Hardy’s inequality as well as its variants in some special cases admit improvements. Further, it is proved that two-variable discrete 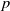$p$-Hardy inequality can also be improved via improved discrete 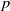$p$-Hardy inequality in one dimension. The result is also extended to the multivariable cases.

Keywords

Hardy’s inequalityVariant Hardy’s inequalityImprovementDouble sequence and seriesMultivariable series

MSC classification

Primary: 26D15: Inequalities for sums, series and integrals
Secondary: 26D10: Inequalities involving derivatives and differential and integral operators
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 67 , Issue 1 , January 2025 , pp. 114 - 130
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Copson, E. T., Note on series of positive terms, J. London Math. Soc. s1-2(1) (1927), 9–12.CrossRefGoogle Scholar
Das, B. and Manna, A., On the improvements of Hardy and Copson inequalities, Revista de la real Academia de Ciencias exactas, Físicas y naturales, Serie A. Matemáticas 117(2) (2023), 18.Google Scholar
Das, B. and Manna, A., On improvements of the Hardy, Copson and Rellich inequalities, https://arxiv.org/abs/2309.04923, (2023), 23 pagesGoogle Scholar
Fischer, F., Keller, M. and Pogorzelski, F., An improved discrete p-Hardy inequality, Integr. Equ. Oper. Theory 95 (2023), 24.CrossRefGoogle Scholar
Gerhat, B., Krejčiřík, D. and Štampach, F., An improved discrete Rellich inequality on the half-line, Israel J. Math. (2024) (To appear).Google Scholar
Gupta, S., Discrete weighted Hardy inequality in 1-D, J. Math. Anal. Appl. 514(2) (2022), 126345.CrossRefGoogle Scholar
Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities, 2nd edition, (Cambridge University Press, London, 1967)Google Scholar
Hardy, G. H., Notes on a theorem of Hilbert, Math. Z. 6 (1920), 314–317.CrossRefGoogle Scholar
Hardy, G. H., Notes on some points in the integral calculus, LX, an inequality between integrals, Messenger of Math. 54 (1925), 150–156.Google Scholar
Hardy, G. H., Notes on some points in the integral calculus, LI.On Hillbert’s double-series theorem,and some connected theorems concerning the convergence of infinite series and integrals, Messenger of Math. 48 (1919), 107–112.Google Scholar
Hardy, G. H., Remarks on three recent notes in the journal, J. London Math. Soc. 3(3) (1928), 166–169.CrossRefGoogle Scholar
Huang, X. and Ye, D., One‐dimensional sharp discrete Hardy–Rellich inequalities, J. London Math. Soc. 109(1) (2024), e12838.CrossRefGoogle Scholar
Keller, M., Pinchover, Y. and Pogorzelski, F., An improved discrete Hardy inequality, Amer. Math. Monthly 125(4) (2018), 347–350.CrossRefGoogle Scholar
Keller, M., Pinchover, Y. and Pogorzelski, F., Optimal Hardy inequalities for Schrödinger operators on graphs, Comm. Math. Phys. 358(2) (2018), 767–790.CrossRefGoogle Scholar
Krejčiřík, D. and Štampach, F., A sharp form of the discrete Hardy inequality and the Keller-Pinchover-Pogorzelski inequality, Amer. Math. Monthly 122(3) (2022), 281–283.CrossRefGoogle Scholar
Krejčiřík, D., Laptev, A. and Štampach, F., Spectral enclosure and stability for non-self-adjoint discrete Schrödinger operator on the half-line, Bull. London Math. Soc. 54(6) (2022), 2379–2403.CrossRefGoogle Scholar
Kufner, A., Maligranda, L. and Persson, L., The prehistory of the Hardy inequality, Amer. Math. Monthly 113(8) (2006), 715–732.CrossRefGoogle Scholar
Landau, E., Letter to G. H. Hardy, June 21, (1921)Google Scholar
Landau, E., Schur, I. and Hardy, G. H., A note on a theorem concerning series of positive terms: extract from a letter of prof, J. London Math. Soc. 1(1926), 38–39.CrossRefGoogle Scholar
Pachpatte, B. G., A many variable generalization of Hardy’s inequality concerning a series of terms, Tamkang J. Math. 23(4) (1992), 349–354.CrossRefGoogle Scholar
Salem, S., Khan, Z. A. A. and Redheffer, R., Note Hardy’s inequality in several variables, J. Math. Anal. Appl. 252 (2000), 989–993.CrossRefGoogle Scholar