Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-25T20:06:46.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagrammatics for the smallest quantum coideal and Jones–Wenzl projectors

Part of: Representation theory of groups Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  22 April 2025

Catharina Stroppel Open the ORCID record for Catharina Stroppel [Opens in a new window]  and
Zbigniew Wojciechowski
Catharina Stroppel*
Affiliation:
Department of Mathematics, University of Bonn, Bonn, Germany
Zbigniew Wojciechowski
Affiliation:
Department of Mathematics, University of Dresden, Dresden, Germany
*
Corresponding author: Catharina Stroppel; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe algebraically, diagrammatically, and in terms of weight vectors, the restriction of tensor powers of the standard representation of quantum 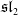$\mathfrak {sl}_2$ to a coideal subalgebra. We realize the category as a module category over the monoidal category of type 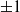$\pm 1$ representations in terms of string diagrams and via generators and relations. The idempotents projecting onto the quantized eigenspaces are described as type 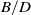$B/D$ analogues of Jones–Wenzl projectors. As an application, we introduce and give recursive formulas for analogues of 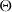$\Theta$-networks.

Keywords

quantum groupsTemperley-Lieb algebrasJones-Wenzl projectors

MSC classification

Primary: 17B37: Quantum groups (quantized enveloping algebras) and related deformations 20C08: Hecke algebras and their representations
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Brochier, A., Cyclotomic associators and finite type invariants for tangles in the solid torus, Algebr. Geom. Topol. 13(6) (2013), 3365–3409.CrossRefGoogle Scholar
Brundan, J. and Stroppel, C., Highest weight categories arising from Khovanov’s diagram algebra III: category O , Represent. Theory 15 (2011), 170–243.CrossRefGoogle Scholar
Bao, H. and Wang, W., A new approach to Kazhdan–Lusztig theory of type B via quantum symmetric pairs, Astérisque. 402 (2018), vii+134 pp.Google Scholar
Brundan, J., Wang, W. and Webster, B., The nil-Brauer category, 2023. arXiv: math/2305.03876Google Scholar
Carter, J. S., Flath, D. E. and Saito, M., The classical and quantum 6j-symbols, Mathematical notes number, vol. 43 (Princeton University Press, 1995).Google Scholar
Cautis, S., Kamnitzer, J. and Morrison, S., Webs and quantum skew Howe duality, Math. Ann. 360(1–2) (2014), 351–390.CrossRefGoogle Scholar
Ehrig, M. and Stroppel, C., Diagrammatic description for the categories of perverse sheaves on isotropic grassmannians, Sel. Math. New Ser. 22(3) (2016), 1455–1536.CrossRefGoogle Scholar
Ehrig, M. and Stroppel, C., Nazarov–Wenzl algebras, coideal subalgebras and categorified skew Howe duality, Adv. Math. 331 (2018), 58–142.CrossRefGoogle Scholar
Frenkel, I., Stroppel, C. and Sussan, J., Categorifying fractional Euler characteristics, Jones–Wenzl projectors and 3j-symbols, Quantum Topol. 3(2) (2012), 181–253.CrossRefGoogle Scholar
Green, R. M., Generalized Temperley–Lieb algebras and decorated tangles, J Knot Theor Ramif. 07(02) (1998), 155–171.CrossRefGoogle Scholar
Häring-Oldenburg, R., Actions of tensor categories, cylinder braids and their Kauffman polynomial, Topology Appl. 112(3) (2001), 297–314.CrossRefGoogle Scholar
Iohara, K., Lehrer, G. and Zhang, R., Schur–Weyl duality for certain infinite dimensional ${U}_q(\mathfrak {sl}_2)$ -modules, Represent. Theory 25 (2021), 265--299.CrossRefGoogle Scholar
Jantzen, J.-C., Lectures on quantum groups, Graduate studies in mathematics, vol. 6 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Kauffman, L. H. and Lins, S. L. S., Temperley–Lieb recoupling theory and invariants of 3-manifolds, Annals of mathematics studies number, vol. 134 (Princeton University Press, 1994).Google Scholar
Khovanov, M. and Lauda, A. D., A diagrammatic approach to categorification of quantum groups I, Represent. Theory 13(14) (2009), 309–347.CrossRefGoogle Scholar
Letzter, G., Coideal subalgebras and quantum symmetric pairs, in New directions in Hopf algebras, volume 43 of Math. Sci. Res. Inst. Publ., (Cambridge Univ. Press, Cambridge, 2002), 117–165.Google Scholar
Letzter, G., Quantum symmetric pairs and their zonal spherical functions, Transform. Groups. 8(3) (2003), 261–292.CrossRefGoogle Scholar
Lickorish, W. B. R., Three-manifolds and the Temperley-Lieb algebra, Math. Ann. 290(1) (1991), 657–670.CrossRefGoogle Scholar
Mathas, A., Cyclotomic quiver Hecke algebras of type A., inModular representation theory of finite and p-adic groups, volume 30 of Lect. Notes Ser. Inst. Math. Sci. Natl. Univ. Singap., (World Sci. Publ, Hackensack, NJ, 2015), 165–266.CrossRefGoogle Scholar
Müller, E. F. and Schneider, H.-J., Quantum homogeneous spaces with faithfully flat module structures, Isr. J. Math. 111(1) (1999), 157–190.CrossRefGoogle Scholar
Masbaum, G. and Vogel, P., 3-valent graphs and the Kauffman bracket, Pac. J. Math. 164(2) (1994), 361–381.CrossRefGoogle Scholar
Queffelec, H. and Wedrich, P., Extremal weight projectors, Math. Res. Lett. 25(6) (2018), 1911–1936.CrossRefGoogle Scholar
Rouquier, R., 2-Kac-Moody algebras, 2008. arXiv: math/0812.5023Google Scholar
Rozansky, L., An infinite torus braid yields a categorified Jones–Wenzl projector, Fund. Math. 225(1) (2014), 305–326.CrossRefGoogle Scholar
Stroppel, C., Categorification: tangle invariants and TQFTs, ICM—International congress of mathematicians, vol. II, (EMS Press, Berlin, 2023), 1312–1353.CrossRefGoogle Scholar
tom Dieck, T., Symmetrische Brücken und Knotentheorie zu den Dynkin-Diagrammen vom Typ B , J. Reine Angew. Math. 451 (1994), 71–88.Google Scholar
tom Dieck, T., Temperley–Lieb algebras associated to the root system D, Arch. Math. 71(5) (1998), 407–416.CrossRefGoogle Scholar
Tingley, P., A minus sign that used to annoy me but now I know why it is there, 2015. arXiv: math/1002.0555Google Scholar
Watanabe, H., Classical weight modules over $\imath$ quantum groups, J. Algebra. 578 (2021), 241–302.CrossRefGoogle Scholar
Watanabe, H., Crystal bases of modified $\imath$ quantum groups of certain quasi-split types, Algebr. Represent. Theory. 27(1) (2024), 1–76.CrossRefGoogle Scholar
Wojciechowski, Z., Categorified Jones–Wenzl projectors and generalizations, 2023. arXiv: math/2310.01131Google Scholar