Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-30T17:46:15.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Transformations of the transfinite plane

Part of: Set theory

Published online by Cambridge University Press:  03 March 2021

Assaf Rinot  and
Jing Zhang
Assaf Rinot
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan5290002, Israel; E-mail: [email protected], [email protected].
Jing Zhang
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan5290002, Israel; E-mail: [email protected], [email protected].

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the existence of transformations of the transfinite plane that allow one to reduce Ramsey-theoretic statements concerning uncountable Abelian groups into classical partition relations for uncountable cardinals.

To exemplify: we prove that for every inaccessible cardinal 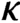$\kappa $, if 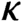$\kappa $ admits a stationary set that does not reflect at inaccessibles, then the classical negative partition relation 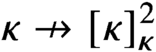$\kappa \nrightarrow [\kappa ]^2_\kappa $ implies that for every Abelian group 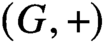$(G,+)$ of size 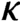$\kappa $, there exists a map 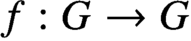$f:G\rightarrow G$ such that for every 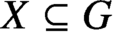$X\subseteq G$ of size 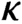$\kappa $ and every 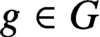$g\in G$, there exist 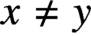$x\neq y$ in X such that 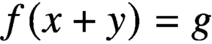$f(x+y)=g$.

MSC classification

Primary: 03E02: Partition relations
Secondary: 03E35: Consistency and independence results
Type
Foundations
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e16
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Brodsky, Ari Meir and Rinot, Assaf. Distributive Aronszajn trees. Fund. Math., 245(3):217–291, 2019.CrossRefGoogle Scholar
Eisworth, Todd. Getting more colors I. J. Symbolic Logic, 78(1):1–16, 2013.CrossRefGoogle Scholar
Eisworth, Todd. Getting more colors II. J. Symbolic Logic, 78(1):17–38, 2013.CrossRefGoogle Scholar
Fernandez-Breton, David and Rinot, Assaf. Strong failures of higher analogs of Hindman’s theorem. Trans. Amer. Math. Soc., 369(12):8939–8966, 2017.CrossRefGoogle Scholar
Hindman, Neil. Finite sums from sequences within cells of a partition of $N$. J. Combinatorial Theory Ser. A, 17:1–11, 1974.CrossRefGoogle Scholar
Hindman, Neil, Leader, Imre, and Strauss, Dona. Pairwise sums in colourings of the reals. Abh. Math. Semin. Univ. Hambg., 87(2):275–287, 2017.CrossRefGoogle Scholar
Hoffman, Douglas J.. A Coloring Theorem for Inaccessible Cardinals. ProQuest LLC, Ann Arbor, MI, 2013.Google Scholar
Inamdar, Tanmay and Rinot, Assaf. Was Ulam right? http://assafrinot.com/paper/47, 2021. In preparation.Google Scholar
Lambie-Hanson, Chris and Rinot, Assaf. Knaster and friends II: The C-sequence number. J. Math. Log., 21(1):2150002, 54, 2021.CrossRefGoogle Scholar
Ramsey, F.P.. On a problem of formal logic. Proc. London Math. Soc., pages 264–286, 1930.CrossRefGoogle Scholar
Rinot, Assaf. Transforming rectangles into squares, with applications to strong colorings. Adv. Math., 231(2):1085–1099, 2012.CrossRefGoogle Scholar
Rinot, Assaf. Chain conditions of products, and weakly compact cardinals. Bull. Symb. Log., 20(3):293–314, 2014.CrossRefGoogle Scholar
Rinot, Assaf. Complicated colorings. Math. Res. Lett., 21(6):1367–1388, 2014.CrossRefGoogle Scholar
Rinot, Assaf. Higher Souslin trees and the GCH, revisited. Adv. Math., 311(C):510–531, 2017.CrossRefGoogle Scholar
Rinot, Assaf and Todorcevic, Stevo. Rectangular square-bracket operation for successor of regular cardinals. Fund. Math., 220(2):119–128, 2013.CrossRefGoogle Scholar
Rinot, Assaf and Zhang, Jing. Strongest transformations. http://assafrinot.com/paper/45, 2021. In preparation.Google Scholar
Shelah, Saharon. Successors of singulars, cofinalities of reduced products of cardinals and productivity of chain conditions. Israel J. Math., 62(2):213–256, 1988.CrossRefGoogle Scholar
Saharon Shelah. There are Jonsson algebras in many inaccessible cardinals. In Cardinal Arithmetic, volume 29 of Oxford Logic Guides. Oxford University Press, 1994.Google Scholar
Shelah, Saharon. Colouring and non-productivity of ${\aleph}_2$-cc. Annals of Pure and Applied Logic, 84:153–174, 1997.CrossRefGoogle Scholar
Sierpiński, Waclaw. Sur un problème de la théorie des relations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (2), 2(3):285–287, 1933.Google Scholar
Soukup, Daniel and Soukup, Lajos. Club guessing for dummies. arXiv preprint arXiv:1003.4670, 2010.Google Scholar
Todorčević, Stevo. Partitioning pairs of countable ordinals. Acta Math., 159(3-4):261–294, 1987.CrossRefGoogle Scholar
Todorcevic, Stevo. Walks on ordinals and their characteristics, volume 263 of Progress in Mathematics. Birkhäuser Verlag, Basel, 2007.CrossRefGoogle Scholar