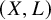1 Introduction
1.1 Historical background and motivation
1.1.1 WDVV equations and Frobenius manifolds
The Witten-Dijkgraaf-Verlinde-Verlinde (WDVV) equation is a system of non-linear partial differential equations for one function, depending on a finite number of variables. One of the most important applications of the WDVV equation is the study of the quantum cohomology of a smooth projective variety
![]() $\mathcal {X}$
over
$\mathcal {X}$
over
![]() $ {\mathbb {C}} $
. Let
$ {\mathbb {C}} $
. Let
![]() $\{T_i\}_{i=1}^m$
be a basis of
$\{T_i\}_{i=1}^m$
be a basis of
![]() $H^{*}(\mathcal {X})$
Footnote
1
and
$H^{*}(\mathcal {X})$
Footnote
1
and
![]() $t^1,\dots ,t^m$
be the corresponding coordinates. Let
$t^1,\dots ,t^m$
be the corresponding coordinates. Let
and
![]() $(g^{ij})=(g_{ij})^{-1}$
. Let
$(g^{ij})=(g_{ij})^{-1}$
. Let
![]() $F_0^{\mathcal {X}}$
be the generating function of genus-zero Gromov-Witten invariants of
$F_0^{\mathcal {X}}$
be the generating function of genus-zero Gromov-Witten invariants of
![]() $\mathcal {X}$
which depends on the variables
$\mathcal {X}$
which depends on the variables
![]() $t^1,\dots ,t^m$
. The following theorem is the WDVV equation in Gromov-Witten theory, first proved in [Reference McDuff and Salamon39, Reference Ruan and Tian41].
$t^1,\dots ,t^m$
. The following theorem is the WDVV equation in Gromov-Witten theory, first proved in [Reference McDuff and Salamon39, Reference Ruan and Tian41].
Theorem 1.1 [Reference McDuff and Salamon39, Reference Ruan and Tian41].
For any
![]() $i,j,k,l\in \{1,\dots ,m\}$
, the following WDVV equation holds:
$i,j,k,l\in \{1,\dots ,m\}$
, the following WDVV equation holds:
 $$ \begin{align*}\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^\nu} \cdot g^{\nu\mu}\cdot \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^\mu\partial t^k\partial t^l} =\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^j\partial t^k\partial t^\nu} \cdot g^{\nu\mu}\cdot \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^\mu\partial t^i\partial t^l}. \end{align*} $$
$$ \begin{align*}\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^\nu} \cdot g^{\nu\mu}\cdot \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^\mu\partial t^k\partial t^l} =\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^j\partial t^k\partial t^\nu} \cdot g^{\nu\mu}\cdot \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^\mu\partial t^i\partial t^l}. \end{align*} $$
The importance of the WDVV equation is that it implies the associativity of the quantum product
![]() $\star _t$
defined by
$\star _t$
defined by
 $$ \begin{align*}(T_i\star_t T_j,T_k)_{\mathcal{X}}=\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^k} \end{align*} $$
$$ \begin{align*}(T_i\star_t T_j,T_k)_{\mathcal{X}}=\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^k} \end{align*} $$
for
![]() $i,j\in \{1,\dots ,m\}$
. The associativity of the quantum product has many important applications. A typical example is the simple, recursive formula given by Kontsevich and Manin [Reference Kontsevich and Manin29] that calculates the Gromov-Witten invariants of
$i,j\in \{1,\dots ,m\}$
. The associativity of the quantum product has many important applications. A typical example is the simple, recursive formula given by Kontsevich and Manin [Reference Kontsevich and Manin29] that calculates the Gromov-Witten invariants of
![]() $\mathbb {P}^2$
. The geometric insight behind the formula is a splitting principle which is captured by the associativity of the quantum product. The WDVV equation and Kontsevich-Manin axioms were then used by Göttsche and Pandharipande [Reference Göttsche and Pandharipande21] to give a set of formulae that recursively compute the Gromov-Witten invariants of
$\mathbb {P}^2$
. The geometric insight behind the formula is a splitting principle which is captured by the associativity of the quantum product. The WDVV equation and Kontsevich-Manin axioms were then used by Göttsche and Pandharipande [Reference Göttsche and Pandharipande21] to give a set of formulae that recursively compute the Gromov-Witten invariants of
![]() $\mathbb {P}^2_r$
, the blowup of
$\mathbb {P}^2_r$
, the blowup of
![]() $\mathbb {P}^2$
at r points.
$\mathbb {P}^2$
at r points.
Moreover, the quantum product determines the structure of a Frobenius manifold.
Definition 1.2. A complex Frobenius manifold consists of the data
![]() $(M,g,A,\mathbf {1})$
where
$(M,g,A,\mathbf {1})$
where
-
1. M is a complex manifold of dimension m;
-
2. g is a flat holomorphic metric on the tangent bundle
 $\mathcal {T}_M$
;
$\mathcal {T}_M$
; -
3. A is a holomorphic tensor
where $$ \begin{align*}A:\mathcal{T}_M\otimes \mathcal{T}_M\otimes \mathcal{T}_M\to \mathcal{O}_M, \end{align*} $$
$$ \begin{align*}A:\mathcal{T}_M\otimes \mathcal{T}_M\otimes \mathcal{T}_M\to \mathcal{O}_M, \end{align*} $$
 $\mathcal {O}_M$
is the sheaf of holomorphic functions on M.
$\mathcal {O}_M$
is the sheaf of holomorphic functions on M.
-
4.
 $\mathbf {1}$
is a holomorphic vector field on M.
$\mathbf {1}$
is a holomorphic vector field on M.
The above data are required to satisfy the following conditions.
-
1. (Potentiality) M is covered by open sets U each equipped with a commuting basis of
 $g-$
flat holomorphic vector fields, and a holomorphic potential function
$g-$
flat holomorphic vector fields, and a holomorphic potential function $$ \begin{align*}X_1,\dots,X_m\in \mathcal{T}_M(U) \end{align*} $$
$$ \begin{align*}X_1,\dots,X_m\in \mathcal{T}_M(U) \end{align*} $$
 $F\in \mathcal {O}_U(U)$
such that
$F\in \mathcal {O}_U(U)$
such that  $$ \begin{align*}A(X_i,X_j,X_k)=X_iX_jX_k(F). \end{align*} $$
$$ \begin{align*}A(X_i,X_j,X_k)=X_iX_jX_k(F). \end{align*} $$
-
2. (Associativity) Define a commutative product
 $\star $
on
$\star $
on
 $\mathcal {T}_M$
by where
$\mathcal {T}_M$
by where $$ \begin{align*}g(X\star Y,Z)=A(X,Y,Z), \end{align*} $$
$$ \begin{align*}g(X\star Y,Z)=A(X,Y,Z), \end{align*} $$
 $X,Y,Z$
are holomorphic vector fields. Then we require that
$X,Y,Z$
are holomorphic vector fields. Then we require that
 $\star $
is associative.
$\star $
is associative.
-
3. (Unit)
 $\mathbf {1}$
is
$\mathbf {1}$
is
 $g-$
flat and is a unit for the product
$g-$
flat and is a unit for the product
 $\star $
.
$\star $
.
The structure of Frobenius manifolds appears in different areas of mathematics including the singularity theory and curve counting theories in algebraic geometry (Gromov-Witten theory, Fan-Jarvis-Ruan-Witten theory). A systematic study of Frobenius manifolds was first done by Dubrovin [Reference Dubrovin11, Reference Dubrovin12]. Again, the associativity of the product
![]() $\star $
is equivalent to the fact that the potential function F in Definition 1.2 satisfies the WDVV equation in Theorem 1.1 by replacing
$\star $
is equivalent to the fact that the potential function F in Definition 1.2 satisfies the WDVV equation in Theorem 1.1 by replacing
![]() $\frac {\partial }{\partial t^i}$
by
$\frac {\partial }{\partial t^i}$
by
![]() $X_i$
. Let
$X_i$
. Let
![]() $\nabla $
be the Levi-Civita connection corresponding to the metric g. For
$\nabla $
be the Levi-Civita connection corresponding to the metric g. For
![]() $z\in \mathbb {P}^1$
, define the Dubrovin connection
$z\in \mathbb {P}^1$
, define the Dubrovin connection
![]() $\nabla ^z$
as
$\nabla ^z$
as
Then it is easy to see that the associativity of
![]() $\star $
is equivalent to the flatness of
$\star $
is equivalent to the flatness of
![]() $\nabla ^z$
and that the commutativity of
$\nabla ^z$
and that the commutativity of
![]() $\star $
is equivalent to the fact that
$\star $
is equivalent to the fact that
![]() $\nabla ^z$
is symmetric.
$\nabla ^z$
is symmetric.
In the case of quantum cohomology, suppose that the genus-zero Gromov-Witten potential
![]() $F_0^{\mathcal {X}}$
is convergent in a neighborhood U of the origin. One may take M to be U and the potential function F to be
$F_0^{\mathcal {X}}$
is convergent in a neighborhood U of the origin. One may take M to be U and the potential function F to be
![]() $F_0^{\mathcal {X}}$
in Definition 1.2. Moreover, let the metric g be given by the Poincaré pairing on
$F_0^{\mathcal {X}}$
in Definition 1.2. Moreover, let the metric g be given by the Poincaré pairing on
![]() $H^{*}(\mathcal {X})$
and
$H^{*}(\mathcal {X})$
and
![]() $\mathbf {1}$
be the identity in
$\mathbf {1}$
be the identity in
![]() $H^{*}(\mathcal {X})$
. Then one obtains a Frobenius manifold. In general, the genus-zero Gromov-Witten potential
$H^{*}(\mathcal {X})$
. Then one obtains a Frobenius manifold. In general, the genus-zero Gromov-Witten potential
![]() $F_0^{\mathcal {X}}$
is not convergent. Then one can replace the above formalism by considering formal Frobenius manifolds (see [Reference Manin35, Reference Lee and Pandharipande30]). Specifically, one can replace the complex manifold M by the formal scheme
$F_0^{\mathcal {X}}$
is not convergent. Then one can replace the above formalism by considering formal Frobenius manifolds (see [Reference Manin35, Reference Lee and Pandharipande30]). Specifically, one can replace the complex manifold M by the formal scheme ![]() over the base ring
over the base ring
![]() $\Lambda _{\mathcal {X}}$
which is the Novikov ring of
$\Lambda _{\mathcal {X}}$
which is the Novikov ring of
![]() $\mathcal {X}$
. Then one may view
$\mathcal {X}$
. Then one may view
![]() $F_0^{\mathcal {X}}$
as a regular function on
$F_0^{\mathcal {X}}$
as a regular function on
![]() $\hat {H}$
and obtain a formal Frobenius manifold. See Section 4 for additional details, including definitions of formal Frobenius manifolds over general base rings.
$\hat {H}$
and obtain a formal Frobenius manifold. See Section 4 for additional details, including definitions of formal Frobenius manifolds over general base rings.
1.1.2 Open WDVV equations and F-manifolds
The open WDVV equation is a system of non-linear partial differential equations that extends the WDVV equation by introducing an additional variable
![]() $t^o$
for the open sector and an additional potential function
$t^o$
for the open sector and an additional potential function
![]() $F^o(t^1,\dots ,t^m,t^o)$
called the open potential function. One of the most important motivations to introduce the open WDVV equation is to study open Gromov-Witten theory. In [Reference Solomon42, Reference Horev and Solomon26, Reference Solomon and Tukachinsky43], open Gromov-Witten invariants of
$F^o(t^1,\dots ,t^m,t^o)$
called the open potential function. One of the most important motivations to introduce the open WDVV equation is to study open Gromov-Witten theory. In [Reference Solomon42, Reference Horev and Solomon26, Reference Solomon and Tukachinsky43], open Gromov-Witten invariants of
![]() $(\mathcal {X},\mathcal {L})$
are studied for certain symplectic manifolds
$(\mathcal {X},\mathcal {L})$
are studied for certain symplectic manifolds
![]() $\mathcal {X}$
and Lagrangian submanifolds
$\mathcal {X}$
and Lagrangian submanifolds
![]() $\mathcal {L}\subset \mathcal {X}$
. In these cases, one can introduce the disk potential
$\mathcal {L}\subset \mathcal {X}$
. In these cases, one can introduce the disk potential
![]() $F^{\mathcal {X},\mathcal {L}}_{0,1}$
which is the generating function of disk Gromov-Witten invariants of
$F^{\mathcal {X},\mathcal {L}}_{0,1}$
which is the generating function of disk Gromov-Witten invariants of
![]() $(\mathcal {X},\mathcal {L})$
. As before, let
$(\mathcal {X},\mathcal {L})$
. As before, let
![]() $\{T_i\}_{i=1}^m$
be a basis of
$\{T_i\}_{i=1}^m$
be a basis of
![]() $H^{*}(\mathcal {X})$
and
$H^{*}(\mathcal {X})$
and
![]() $t^1,\dots ,t^m$
be the corresponding coordinates. We still consider the Poincaré pairing
$t^1,\dots ,t^m$
be the corresponding coordinates. We still consider the Poincaré pairing
![]() $g_{ij}=( T_i,T_j)_{\mathcal {X}}=\int _{\mathcal {X}}T_i\cup T_j$
and let
$g_{ij}=( T_i,T_j)_{\mathcal {X}}=\int _{\mathcal {X}}T_i\cup T_j$
and let
![]() $(g^{ij})=(g_{ij})^{-1}$
. Let
$(g^{ij})=(g_{ij})^{-1}$
. Let
![]() $F_0^{\mathcal {X}}$
be the generating function of genus-zero Gromov-Witten invariants of
$F_0^{\mathcal {X}}$
be the generating function of genus-zero Gromov-Witten invariants of
![]() $\mathcal {X}$
, which depends on the variables
$\mathcal {X}$
, which depends on the variables
![]() $t^1,\dots ,t^m$
but is independent of the additional variable
$t^1,\dots ,t^m$
but is independent of the additional variable
![]() $t^o$
. On the other hand, the disk potential
$t^o$
. On the other hand, the disk potential
![]() $F^{\mathcal {X},\mathcal {L}}_{0,1}$
depends on
$F^{\mathcal {X},\mathcal {L}}_{0,1}$
depends on
![]() $t^1,\dots ,t^m$
as well as
$t^1,\dots ,t^m$
as well as
![]() $t^o$
. The variable
$t^o$
. The variable
![]() $t^o$
encodes the point-like insertions from the boundary marked points of the domain disk (see [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] for more details). The following open WDVV equation is proved in [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43].
$t^o$
encodes the point-like insertions from the boundary marked points of the domain disk (see [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] for more details). The following open WDVV equation is proved in [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43].
Theorem 1.3 [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43].
For any
![]() $i,j,k\in \{1,\dots ,m\}$
, the following open WDVV equation holds:
$i,j,k\in \{1,\dots ,m\}$
, the following open WDVV equation holds:
 $$ \begin{align*} \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^\mu}g^{\mu\nu}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^\nu\partial t^k} +\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^i\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^k} &= \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^k\partial t^j\partial t^\mu}g^{\mu\nu}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^\nu\partial t^i}+\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^k\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^i},\\ \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^\mu}g^{\mu\nu}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^\nu\partial t^o}+\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^i\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{(\partial t^o)^2}&= \frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^i}. \end{align*} $$
$$ \begin{align*} \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^\mu}g^{\mu\nu}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^\nu\partial t^k} +\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^i\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^k} &= \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^k\partial t^j\partial t^\mu}g^{\mu\nu}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^\nu\partial t^i}+\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^k\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^i},\\ \frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^\mu}g^{\mu\nu}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^\nu\partial t^o}+\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^i\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{(\partial t^o)^2}&= \frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^j}\frac{\partial^2 F^{\mathcal{X},\mathcal{L}}_{0,1}}{\partial t^o\partial t^i}. \end{align*} $$
The open WDVV equation has also been studied in [Reference Pandharipande, Solomon and Tessler40, Reference Alcolado1, Reference Buryak, Clader and Tessler7, Reference Buryak, Clader and Tessler8, Reference Basalaev and Buryak4, Reference Chen and Zinger10, Reference Arsie, Buryak, Lorenzoni and Rossi3].
The natural structure that captures the open WDVV equation is that of a flat F-manifold (see, for example, [Reference Hertling and Manin24, Reference Manin35, Reference Getzler20, Reference Manin36, Reference Arsie, Buryak, Lorenzoni and Rossi3]), a generalization of a Frobenius manifold.
Definition 1.4. A flat complex F-manifold consists of the data
![]() $(M,\nabla ,\star ,\mathbf {1})$
where
$(M,\nabla ,\star ,\mathbf {1})$
where
-
1. M is a complex manifold of dimension
 $m+1$
,
$m+1$
, -
2.
 $\nabla $
is a holomorphic connection on the tangent bundle
$\nabla $
is a holomorphic connection on the tangent bundle
 $\mathcal {T}_M$
,
$\mathcal {T}_M$
, -
3.
 $(\mathcal {T}_M \big |_p,\star )$
defines an algebra structure on each tangent space, analytically depending on the point
$(\mathcal {T}_M \big |_p,\star )$
defines an algebra structure on each tangent space, analytically depending on the point
 $p\in M$
,
$p\in M$
, -
4.
 $\mathbf {1}$
is a
$\mathbf {1}$
is a
 $\nabla $
-flat vector field which is a unit for
$\nabla $
-flat vector field which is a unit for
 $\star $
.
$\star $
.
The above data satisfy the condition that the connection
![]() $\nabla ^z:=\nabla -\frac {1}{z}\star $
is flat and symmetric for any
$\nabla ^z:=\nabla -\frac {1}{z}\star $
is flat and symmetric for any
![]() $z\in \mathbb {P}^1$
.
$z\in \mathbb {P}^1$
.
The structure of F-manifolds appears in different areas of mathematics including the open Gromov-Witten theory, Painlevé transcendents, and reflection groups. Again, the associativity of
![]() $\star $
is equivalent to the flatness of
$\star $
is equivalent to the flatness of
![]() $\nabla ^z$
and that the commutativity of
$\nabla ^z$
and that the commutativity of
![]() $\star $
is equivalent to the fact that
$\star $
is equivalent to the fact that
![]() $\nabla ^z$
is symmetric. Moreover, if one chooses flat coordinates
$\nabla ^z$
is symmetric. Moreover, if one chooses flat coordinates
![]() $t^1,\dots ,t^{m+1}$
for the connection
$t^1,\dots ,t^{m+1}$
for the connection
![]() $\nabla $
, then it is easy to see that locally there exist holomorphic functions
$\nabla $
, then it is easy to see that locally there exist holomorphic functions
![]() $F^i(t^1,\dots ,t^{m+1})$
,
$F^i(t^1,\dots ,t^{m+1})$
,
![]() $i = 1, \dots , m+1$
, such that the second derivatives
$i = 1, \dots , m+1$
, such that the second derivatives
are the structure constants of the algebra
![]() $(\mathcal {T}_M \big |_p,\star )$
:
$(\mathcal {T}_M \big |_p,\star )$
:
Then the associativity of
![]() $\star $
is equivalent to the equation
$\star $
is equivalent to the equation
for
![]() $i,j,k,l\in \{1,\dots ,m+1\}$
. The
$i,j,k,l\in \{1,\dots ,m+1\}$
. The
![]() $(m+1)-$
tuple
$(m+1)-$
tuple
![]() $\overline {F}=(F^1,\dots ,F^{m+1})$
is called the vector potential for the F-manifold M. In the special case when M is a Frobenius manifold with potential F, and assuming that
$\overline {F}=(F^1,\dots ,F^{m+1})$
is called the vector potential for the F-manifold M. In the special case when M is a Frobenius manifold with potential F, and assuming that
![]() $g = \mathrm {Id}$
for simplicity, the vector potential is given by
$g = \mathrm {Id}$
for simplicity, the vector potential is given by
![]() $\overline {F}=(\frac {\partial F}{\partial t^1},\dots ,\frac {\partial F}{\partial t^{m+1}})$
.
$\overline {F}=(\frac {\partial F}{\partial t^1},\dots ,\frac {\partial F}{\partial t^{m+1}})$
.
In the case of the open Gromov-Witten theory of
![]() $(\mathcal {X}, \mathcal {L})$
with point-like boundary insertions, one can construct a flat F-manifold as follows. First, we can choose
$(\mathcal {X}, \mathcal {L})$
with point-like boundary insertions, one can construct a flat F-manifold as follows. First, we can choose
![]() $\{T_i\}_{i=1}^m$
such that
$\{T_i\}_{i=1}^m$
such that
![]() $g=\mathrm {Id}$
. Let
$g=\mathrm {Id}$
. Let
![]() $\nabla $
be the connection under which
$\nabla $
be the connection under which
![]() $\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m},\frac {\partial }{\partial t^o}$
are flat. Finally, define the vector potential by
$\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m},\frac {\partial }{\partial t^o}$
are flat. Finally, define the vector potential by
 $$ \begin{align*}\overline{F} := (\frac{\partial F_0^{\mathcal{X}}}{\partial t^1},\dots,\frac{\partial F_0^{\mathcal{X}}}{\partial t^m},F^{\mathcal{X},\mathcal{L}}_{0,1}). \end{align*} $$
$$ \begin{align*}\overline{F} := (\frac{\partial F_0^{\mathcal{X}}}{\partial t^1},\dots,\frac{\partial F_0^{\mathcal{X}}}{\partial t^m},F^{\mathcal{X},\mathcal{L}}_{0,1}). \end{align*} $$
In the case when
![]() $\overline {F}$
is convergent, we obtain a complex F-manifold of dimension
$\overline {F}$
is convergent, we obtain a complex F-manifold of dimension
![]() $m+1$
. Equation (1) is obtained by the open and closed WDVV equations (Theorems 1.1 and 1.3). In general, the vector potential
$m+1$
. Equation (1) is obtained by the open and closed WDVV equations (Theorems 1.1 and 1.3). In general, the vector potential
![]() $\overline {F}$
is not convergent, and one can construct a formal F-manifold as in the case of the quantum cohomology.
$\overline {F}$
is not convergent, and one can construct a formal F-manifold as in the case of the quantum cohomology.
1.1.3 Open WDVV equations for toric Calabi-Yau 3-folds
In this paper, we study the open WDVV equation for
![]() $(X,L)$
where X is a toric Calabi-Yau 3-fold and
$(X,L)$
where X is a toric Calabi-Yau 3-fold and
![]() $L\subset X$
is an outer Aganagic-Vafa brane. We first obtain a collection of non-linear partial differential equations (Proposition 4.4) which involve both the generating function
$L\subset X$
is an outer Aganagic-Vafa brane. We first obtain a collection of non-linear partial differential equations (Proposition 4.4) which involve both the generating function
![]() $F_0^{X,T'}$
of genus-zero equivariant Gromov-Witten invariants of X and the generating function
$F_0^{X,T'}$
of genus-zero equivariant Gromov-Witten invariants of X and the generating function
![]() $F_{0,1}^{X,(L,f)}$
of equivariant disk Gromov-Witten invariants of
$F_{0,1}^{X,(L,f)}$
of equivariant disk Gromov-Witten invariants of
![]() $(X,L)$
. We will package these equations in two different ways to obtain two versions of the open WDVV equation. The first version leads to the construction of a semi-simple formal Frobenius manifold, and the second version leads to a flat formal F-manifold, both exhibiting the recursive structures of the open and closed Gromov-Witten theory of
$(X,L)$
. We will package these equations in two different ways to obtain two versions of the open WDVV equation. The first version leads to the construction of a semi-simple formal Frobenius manifold, and the second version leads to a flat formal F-manifold, both exhibiting the recursive structures of the open and closed Gromov-Witten theory of
![]() $(X,L)$
.
$(X,L)$
.
The key technique we use to derive the open WDVV equation is the open/closed correspondence [Reference Liu and Yu33, Reference Liu and Yu34] which relates the open Gromov-Witten theory of
![]() $(X,L)$
and the closed Gromov-Witten theory of a corresponding toric Calabi-Yau 4-fold
$(X,L)$
and the closed Gromov-Witten theory of a corresponding toric Calabi-Yau 4-fold
![]() $\widetilde {X}$
. Based on the original conjectures of Mayr [Reference Mayr38] in physics, the mathematical development of the correspondence emerges from studies of correspondences among different types (open, relative/log, local) of Gromov-Witten invariants in the literature [Reference Li, Liu, Liu and Zhou31, Reference Fang and Liu13, Reference van Garrel, Graber and Ruddat16, Reference Bousseau, Brini and van Garrel5, Reference Gräfnitz, Ruddat and Zaslow23]. Under this correspondence, we may recover both
$\widetilde {X}$
. Based on the original conjectures of Mayr [Reference Mayr38] in physics, the mathematical development of the correspondence emerges from studies of correspondences among different types (open, relative/log, local) of Gromov-Witten invariants in the literature [Reference Li, Liu, Liu and Zhou31, Reference Fang and Liu13, Reference van Garrel, Graber and Ruddat16, Reference Bousseau, Brini and van Garrel5, Reference Gräfnitz, Ruddat and Zaslow23]. Under this correspondence, we may recover both
![]() $F_{0,1}^{X,(L,f)}$
and
$F_{0,1}^{X,(L,f)}$
and
![]() $F_0^{X,T'}$
from the generating function
$F_0^{X,T'}$
from the generating function
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
of genus-zero equivariant Gromov-Witten invariants of
$F_0^{\widetilde {X},\widetilde {T}'}$
of genus-zero equivariant Gromov-Witten invariants of
![]() $\widetilde {X}$
. The open WDVV equation for
$\widetilde {X}$
. The open WDVV equation for
![]() $(X,L)$
is then a consequence of the usual WDVV equation for
$(X,L)$
is then a consequence of the usual WDVV equation for
![]() $\widetilde {X}$
. Recently, the open/closed correspondence has also been applied to study the integrality properties of Gromov-Witten invariants of
$\widetilde {X}$
. Recently, the open/closed correspondence has also been applied to study the integrality properties of Gromov-Witten invariants of
![]() $(X,L)$
and
$(X,L)$
and
![]() $\widetilde {X}$
(in terms of BPS or Gopakumar-Vafa invariants) [Reference Yu44]. The correspondence has also been studied on the B-model side of mirror symmetry [Reference Liu and Yu34] and extended to quintic 3-folds [Reference Aleshkin and Liu2].
$\widetilde {X}$
(in terms of BPS or Gopakumar-Vafa invariants) [Reference Yu44]. The correspondence has also been studied on the B-model side of mirror symmetry [Reference Liu and Yu34] and extended to quintic 3-folds [Reference Aleshkin and Liu2].
We now discuss our main results and techniques in more detail.
1.2 Statement of the main results
Let X be a smooth toric Calabi-Yau 3-fold and
![]() $T\cong ( {\mathbb {C}} ^{*})^3$
be the algebraic 3-torus embedded in X as a dense open subset. Let
$T\cong ( {\mathbb {C}} ^{*})^3$
be the algebraic 3-torus embedded in X as a dense open subset. Let
![]() $T' \cong ( {\mathbb {C}} ^{*})^2$
be the Calabi-Yau
$T' \cong ( {\mathbb {C}} ^{*})^2$
be the Calabi-Yau
![]() $2$
-subtorus of T which acts trivially on the canonical bundle of X. Let
$2$
-subtorus of T which acts trivially on the canonical bundle of X. Let
![]() $L \subset X$
be an Aganagic-Vafa outer brane in X which is a Lagrangian submanifold diffeomorphic to
$L \subset X$
be an Aganagic-Vafa outer brane in X which is a Lagrangian submanifold diffeomorphic to
![]() $S^1 \times {\mathbb {C}} $
. It intersects a unique T-invariant line
$S^1 \times {\mathbb {C}} $
. It intersects a unique T-invariant line
![]() $l\cong {\mathbb {C}} $
in X. Moreover, L is invariant under the action of the maximal compact subtorus
$l\cong {\mathbb {C}} $
in X. Moreover, L is invariant under the action of the maximal compact subtorus
![]() $T_{\mathbb {R}}' \cong U(1)^2$
of
$T_{\mathbb {R}}' \cong U(1)^2$
of
![]() $T'$
. We further take an integer f called the framing on the Aganagic-Vafa brane L, and construct a 1-dimensional subtorus
$T'$
. We further take an integer f called the framing on the Aganagic-Vafa brane L, and construct a 1-dimensional subtorus
![]() $T_f\subset T'$
.
$T_f\subset T'$
.
Under the open/closed correspondence, the closed geometry corresponding to the open geometry
![]() $(X,L,f)$
is a smooth toric Calabi-Yau 4-fold
$(X,L,f)$
is a smooth toric Calabi-Yau 4-fold
![]() $\widetilde {X}$
that takes the form
$\widetilde {X}$
that takes the form
where
![]() $X \sqcup D$
is a toric partial compactification of X given by adding an additional toric divisor D. In
$X \sqcup D$
is a toric partial compactification of X given by adding an additional toric divisor D. In
![]() $X \sqcup D$
, the T-invariant line
$X \sqcup D$
, the T-invariant line
![]() $l \cong {\mathbb {C}} $
that L intersects is compactified by an additional T-fixed point into a
$l \cong {\mathbb {C}} $
that L intersects is compactified by an additional T-fixed point into a
![]() $\mathbb {P}^1$
whose normal bundle is isomorphic to
$\mathbb {P}^1$
whose normal bundle is isomorphic to
![]() $\mathcal {O}_{\mathbb {P}^1}(f) \oplus \mathcal {O}_{\mathbb {P}^1}(-f-1)$
. There is an inclusion
$\mathcal {O}_{\mathbb {P}^1}(f) \oplus \mathcal {O}_{\mathbb {P}^1}(-f-1)$
. There is an inclusion
Let
![]() $\widetilde {T} \cong ( {\mathbb {C}} ^{*})^4$
be the algebraic 4-torus of
$\widetilde {T} \cong ( {\mathbb {C}} ^{*})^4$
be the algebraic 4-torus of
![]() $\widetilde {X}$
and
$\widetilde {X}$
and
![]() $\widetilde {T}' \cong ( {\mathbb {C}} ^{*})^3$
be the Calabi-Yau 3-subtorus of
$\widetilde {T}' \cong ( {\mathbb {C}} ^{*})^3$
be the Calabi-Yau 3-subtorus of
![]() $\widetilde {T}$
, which contains
$\widetilde {T}$
, which contains
![]() $T'$
as a subtorus. We take the following notations for the equivariant parameters of the tori:
$T'$
as a subtorus. We take the following notations for the equivariant parameters of the tori:
 $$ \begin{align*} & R_{\widetilde{T}'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4], && S_{\widetilde{T}'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4),\\ & R_{T'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2], && S_{T'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2),\\ & R_{T_f} := H^{*}_{T_f}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1], && S_{T_f}:= {\mathbb{C}} (\mathsf{u}_1). \end{align*} $$
$$ \begin{align*} & R_{\widetilde{T}'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4], && S_{\widetilde{T}'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4),\\ & R_{T'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2], && S_{T'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2),\\ & R_{T_f} := H^{*}_{T_f}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1], && S_{T_f}:= {\mathbb{C}} (\mathsf{u}_1). \end{align*} $$
Let
![]() $p_1, \dots , p_m$
be a fixed ordering of the
$p_1, \dots , p_m$
be a fixed ordering of the
![]() $T'$
-fixed points of X and
$T'$
-fixed points of X and
![]() $\widetilde {p}_1, \dots , \widetilde {p}_m$
denote the corresponding
$\widetilde {p}_1, \dots , \widetilde {p}_m$
denote the corresponding
![]() $\widetilde {T}'$
-fixed points of
$\widetilde {T}'$
-fixed points of
![]() $\widetilde {X}$
. We denote the additional
$\widetilde {X}$
. We denote the additional
![]() $\widetilde {T}'$
-fixed point of
$\widetilde {T}'$
-fixed point of
![]() $\widetilde {X}$
by
$\widetilde {X}$
by
![]() $\widetilde {p}_{m+1}$
. We consider the basis
$\widetilde {p}_{m+1}$
. We consider the basis
![]() $\{\phi _1,\dots ,\phi _m\}$
of
$\{\phi _1,\dots ,\phi _m\}$
of
![]() $H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
defined by the fixed points as
$H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
defined by the fixed points as
which forms a canonical basis of the semi-simple Frobenius algebra
where
![]() $\cup $
is the cup product and
$\cup $
is the cup product and
![]() $(-,-)_{X, T'}$
is the
$(-,-)_{X, T'}$
is the
![]() $T'$
-equivariant Poincaré pairing on X. Similarly, we define the basis
$T'$
-equivariant Poincaré pairing on X. Similarly, we define the basis
![]() $\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m,\widetilde {\phi }_{m+1} \}$
of
$\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m,\widetilde {\phi }_{m+1} \}$
of
![]() $H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
as
$H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
as
 $$ \begin{align*}\widetilde{\phi}_i := \frac{[\widetilde{p}_i]}{e_{\widetilde{T}'}(T_{\widetilde{p}_i}\widetilde{X})}, \end{align*} $$
$$ \begin{align*}\widetilde{\phi}_i := \frac{[\widetilde{p}_i]}{e_{\widetilde{T}'}(T_{\widetilde{p}_i}\widetilde{X})}, \end{align*} $$
which forms a canonical basis of the semi-simple Frobenius algebra
Let
![]() $t^1,\dots ,t^m,t^{m+1}$
be the coordinates corresponding to the basis
$t^1,\dots ,t^m,t^{m+1}$
be the coordinates corresponding to the basis
![]() $\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m,\widetilde {\phi }_{m+1} \}$
. Under the correspondence between
$\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m,\widetilde {\phi }_{m+1} \}$
. Under the correspondence between
![]() $\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m\}$
and
$\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m\}$
and
![]() $\{\phi _1,\dots ,\phi _m\}$
, we also view
$\{\phi _1,\dots ,\phi _m\}$
, we also view
![]() $t^1,\dots ,t^m$
as coordinates corresponding to the basis
$t^1,\dots ,t^m$
as coordinates corresponding to the basis
![]() $\{\phi _1,\dots ,\phi _m\}$
.
$\{\phi _1,\dots ,\phi _m\}$
.
We will use the above bases to define the following generating functions of Gromov-Witten invariants over suitable Novikov rings:
-
•
 $F_0^{X,T'}(t^1, \dots , t^m)$
– the generating function of genus-zero
$F_0^{X,T'}(t^1, \dots , t^m)$
– the generating function of genus-zero
 $T'$
-equivariant closed Gromov-Witten invariants of X;
$T'$
-equivariant closed Gromov-Witten invariants of X; -
•
 $F_{0,1}^{X,(L,f)}(t^1, \dots , t^m, t^o)$
– the generating function of genus-zero
$F_{0,1}^{X,(L,f)}(t^1, \dots , t^m, t^o)$
– the generating function of genus-zero
 $T_f$
-equivariant disk invariants of
$T_f$
-equivariant disk invariants of
 $(X,L)$
with framing f, depending on an additional formal variable
$(X,L)$
with framing f, depending on an additional formal variable
 $t^o$
for the open sector;
$t^o$
for the open sector; -
•
 $F_0^{\widetilde {X},\widetilde {T}'}(t^1, \dots , t^m, t^{m+1})$
– the generating function of genus-zero
$F_0^{\widetilde {X},\widetilde {T}'}(t^1, \dots , t^m, t^{m+1})$
– the generating function of genus-zero
 $\widetilde {T}'$
-equivariant closed Gromov-Witten invariants of
$\widetilde {T}'$
-equivariant closed Gromov-Witten invariants of
 $\widetilde {X}$
.
$\widetilde {X}$
.
See Section 3 for detailed definitions. In particular, we will see that the dependence of
![]() $F_{0,1}^{X,(L,f)}$
on the additional open variable
$F_{0,1}^{X,(L,f)}$
on the additional open variable
![]() $t^o$
is captured by terms of form
$t^o$
is captured by terms of form
![]() $(e^{t^o}\mathsf {X}_0)^d$
,
$(e^{t^o}\mathsf {X}_0)^d$
,
![]() $d \in \mathbb {Z}_{>0}$
, where
$d \in \mathbb {Z}_{>0}$
, where
![]() $\mathsf {X}_0$
is a Novikov variable for the relative curve class. The term
$\mathsf {X}_0$
is a Novikov variable for the relative curve class. The term
![]() $\mathsf {X}=e^{t^o}\mathsf {X}_0$
is viewed as encoding the winding number d of the disk invariants.
$\mathsf {X}=e^{t^o}\mathsf {X}_0$
is viewed as encoding the winding number d of the disk invariants.
The open/closed correspondence (see Theorem 3.1) retrieves both
![]() $F_0^{X,T'}$
and
$F_0^{X,T'}$
and
![]() $F_{0,1}^{X,(L,f)}$
from
$F_{0,1}^{X,(L,f)}$
from
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
under a suitable change of coordinates and Novikov variables. The WDVV equation for
$F_0^{\widetilde {X},\widetilde {T}'}$
under a suitable change of coordinates and Novikov variables. The WDVV equation for
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
(Theorem 1.1) then gives rise to a collection of non-linear partial differential equations involving
$F_0^{\widetilde {X},\widetilde {T}'}$
(Theorem 1.1) then gives rise to a collection of non-linear partial differential equations involving
![]() $F_0^{X,T'}$
and
$F_0^{X,T'}$
and
![]() $F_{0,1}^{X,(L,f)}$
(see Proposition 4.4). This collection recovers the WDVV equation for
$F_{0,1}^{X,(L,f)}$
(see Proposition 4.4). This collection recovers the WDVV equation for
![]() $F_0^{X,T'}$
, and contains equations analogous to the open WDVV equation obtained by [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] (Theorem 1.3). As our main results, we use this collection of equations to construct a semi-simple formal Frobenius manifold and a flat formal F-manifold to package the structures of the open and closed Gromov-Witten theory of
$F_0^{X,T'}$
, and contains equations analogous to the open WDVV equation obtained by [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] (Theorem 1.3). As our main results, we use this collection of equations to construct a semi-simple formal Frobenius manifold and a flat formal F-manifold to package the structures of the open and closed Gromov-Witten theory of
![]() $(X,L)$
.
$(X,L)$
.
1.2.1 A formal Frobenius manifold
The first aspect of our constructions is a formal Frobenius manifold (Section 5.1). Consider the formal scheme
over the base ring
where
![]() $\Lambda _{X,L}^{T_f}$
is the
$\Lambda _{X,L}^{T_f}$
is the
![]() $T_f$
-equivariant Novikov ring of
$T_f$
-equivariant Novikov ring of
![]() $(X,L)$
and
$(X,L)$
and
![]() $\epsilon $
is a nilpotent variable with
$\epsilon $
is a nilpotent variable with
![]() $\epsilon ^2 = 0$
. We will define a pairing
$\epsilon ^2 = 0$
. We will define a pairing
![]() $\left (\frac {\partial }{\partial t^i},\frac {\partial }{\partial t^j}\right ) = h_{ij}$
,
$\left (\frac {\partial }{\partial t^i},\frac {\partial }{\partial t^j}\right ) = h_{ij}$
,
![]() $i,j = 1, \dots , m, o$
, on the tangent bundle
$i,j = 1, \dots , m, o$
, on the tangent bundle
![]() $\mathcal {T}_{\hat {H}_1}$
of
$\mathcal {T}_{\hat {H}_1}$
of
![]() $\hat {H}_1$
which is spanned by vector fields
$\hat {H}_1$
which is spanned by vector fields
![]() $\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m}, \frac {\partial }{\partial t^o}$
. Let
$\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m}, \frac {\partial }{\partial t^o}$
. Let
![]() $(h^{ij})=(h_{ij})^{-1}$
. Moreover, we define the potential function F by
$(h^{ij})=(h_{ij})^{-1}$
. Moreover, we define the potential function F by
where the weight restriction
![]() $\mathsf {u}_2 - f\mathsf {u}_1 = 0$
corresponds to the inclusion
$\mathsf {u}_2 - f\mathsf {u}_1 = 0$
corresponds to the inclusion
![]() $T_f \subset T'$
and the symbol
$T_f \subset T'$
and the symbol
![]() $\int $
represents taking the antiderivative with respect to
$\int $
represents taking the antiderivative with respect to
![]() $t^o$
. We show that F satisfies the following WDVV equation.
$t^o$
. We show that F satisfies the following WDVV equation.
Proposition 1.5 (See Proposition 5.3).
For any
![]() $i,j,k,l\in \{1,\dots ,m, o\}$
, the following WDVV equation holds:
$i,j,k,l\in \{1,\dots ,m, o\}$
, the following WDVV equation holds:
In particular, the potential F defines a product
![]() $\star _t$
on
$\star _t$
on
![]() $\mathcal {T}_{\hat {H}_1}$
that is compatible with the metric h and associative. We have the following main structural result.
$\mathcal {T}_{\hat {H}_1}$
that is compatible with the metric h and associative. We have the following main structural result.
Theorem 1.6 (See Theorems 5.5, 5.6).
The tuple
![]() $(\hat {H}_1,F,(-,-))$
is a semi-simple formal Frobenius manifold over
$(\hat {H}_1,F,(-,-))$
is a semi-simple formal Frobenius manifold over
![]() $\Lambda _{X,L}^{T_f}[\epsilon ]$
.
$\Lambda _{X,L}^{T_f}[\epsilon ]$
.
Remark 1.7. One way to interpret the variable
![]() $\epsilon $
is the following. Consider
$\epsilon $
is the following. Consider
![]() $\hat {H}_1$
as a formal supermanifold over
$\hat {H}_1$
as a formal supermanifold over
![]() $\Lambda _{X,L}^{T_f}$
with local coordinates
$\Lambda _{X,L}^{T_f}$
with local coordinates
![]() $t^1,\dots ,t^m,t^o,\epsilon $
where
$t^1,\dots ,t^m,t^o,\epsilon $
where
![]() $t^1,\dots ,t^m,t^o$
are even coordinates and
$t^1,\dots ,t^m,t^o$
are even coordinates and
![]() $\epsilon $
is an odd coordinate (and hence,
$\epsilon $
is an odd coordinate (and hence,
![]() $\epsilon ^2=0$
). Then the pairing h and the product structure
$\epsilon ^2=0$
). Then the pairing h and the product structure
![]() $\star _t$
may be viewed as defined on the subbundle of the tangent bundle spanned by the even vector fields
$\star _t$
may be viewed as defined on the subbundle of the tangent bundle spanned by the even vector fields
![]() $\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m}, \frac {\partial }{\partial t^o}$
. The product
$\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m}, \frac {\partial }{\partial t^o}$
. The product
![]() $\star _t$
itself does not involve the odd vector field
$\star _t$
itself does not involve the odd vector field
![]() $\frac {\partial }{\partial \epsilon }$
. Rather, as remarked in, for example, [Reference Manin and Merkulov37, Section 4.1],
$\frac {\partial }{\partial \epsilon }$
. Rather, as remarked in, for example, [Reference Manin and Merkulov37, Section 4.1],
![]() $\epsilon $
is regarded as an odd structural constant pulled back from the base
$\epsilon $
is regarded as an odd structural constant pulled back from the base
![]() $\mathrm {Spec} (\Lambda _{X,L}^{T_f}[\epsilon ])$
viewed also as a supermanifold over
$\mathrm {Spec} (\Lambda _{X,L}^{T_f}[\epsilon ])$
viewed also as a supermanifold over
![]() $\Lambda _{X,L}^{T_f}$
.
$\Lambda _{X,L}^{T_f}$
.
1.2.2 A flat formal F-manifold
The second aspect of our constructions is a flat formal F-manifold (Section 5.2). Consider the formal scheme
over the base ring
![]() $\Lambda _{X,L}^{T_f}$
, where as compared to
$\Lambda _{X,L}^{T_f}$
, where as compared to
![]() $\hat {H}_1$
above, the variable
$\hat {H}_1$
above, the variable
![]() $\epsilon $
is dropped. Let
$\epsilon $
is dropped. Let
![]() $\nabla $
be the flat connection on the tangent bundle
$\nabla $
be the flat connection on the tangent bundle
![]() $\mathcal {T}_{\hat {H}_2}$
of
$\mathcal {T}_{\hat {H}_2}$
of
![]() $\hat {H}_2$
under which
$\hat {H}_2$
under which
![]() $\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m},\frac {\partial }{\partial t^o}$
are flat. We define the vector potential
$\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m},\frac {\partial }{\partial t^o}$
are flat. We define the vector potential
![]() $\overline {F} = (F^1, \dots , F^m, F^o)$
by
$\overline {F} = (F^1, \dots , F^m, F^o)$
by
 $$ \begin{align*} & F^i := h^{ii} \frac{\partial}{\partial t^i} \left(F_0^{X,T'}\big|_{\mathsf{u}_2-f\mathsf{u}_1=0}+\int F_{0,1}^{X,(L,f)} \big|_{t^o = 0}\right), && i = 1, \dots, m,\\ &F^o := F_{0,1}^{X,(L,f)} \big|_{t^o = 0}. \end{align*} $$
$$ \begin{align*} & F^i := h^{ii} \frac{\partial}{\partial t^i} \left(F_0^{X,T'}\big|_{\mathsf{u}_2-f\mathsf{u}_1=0}+\int F_{0,1}^{X,(L,f)} \big|_{t^o = 0}\right), && i = 1, \dots, m,\\ &F^o := F_{0,1}^{X,(L,f)} \big|_{t^o = 0}. \end{align*} $$
Here,
![]() $t^o$
is still viewed as the variable for the ‘open state space’, while we should notice that each component of
$t^o$
is still viewed as the variable for the ‘open state space’, while we should notice that each component of
![]() $\overline {F}$
is independent of
$\overline {F}$
is independent of
![]() $t^o$
. We show that
$t^o$
. We show that
![]() $\overline {F}$
satisfies the following open WDVV equation.
$\overline {F}$
satisfies the following open WDVV equation.
Proposition 1.8 (See Proposition 5.9).
For any
![]() $i,j,k,l\in \{1,\dots ,m, o\}$
, the following open WDVV equation holds:
$i,j,k,l\in \{1,\dots ,m, o\}$
, the following open WDVV equation holds:
In particular, the vector potential
![]() $\overline {F}$
defines a product structure
$\overline {F}$
defines a product structure
![]() $\star _t$
on
$\star _t$
on
![]() $\mathcal {T}_{\hat {H}_2}$
that is associative. Analyzing the structural constants and using that
$\mathcal {T}_{\hat {H}_2}$
that is associative. Analyzing the structural constants and using that
![]() $\overline {F}$
is independent of
$\overline {F}$
is independent of
![]() $t^o$
, we show that
$t^o$
, we show that
![]() $\star _t$
does not admit an identity field and
$\star _t$
does not admit an identity field and
![]() $\frac {\partial }{\partial t^o}$
is nilpotent. We arrive at the following main structural result.
$\frac {\partial }{\partial t^o}$
is nilpotent. We arrive at the following main structural result.
Theorem 1.9 (See Theorem 5.11).
The tuple
![]() $(\hat {H}_2, \nabla , \star _t)$
is a flat formal F-manifold without unit over
$(\hat {H}_2, \nabla , \star _t)$
is a flat formal F-manifold without unit over
![]() $\Lambda _{X,L}^{T_f}$
in which the
$\Lambda _{X,L}^{T_f}$
in which the
![]() $t^o$
-direction is nilpotent.
$t^o$
-direction is nilpotent.
F-cohomological field theories without unit have been studied in [Reference Arsie, Buryak, Lorenzoni and Rossi3, Reference Buryak and Gubarevich9].
Remark 1.10. The situation here is in a sense opposite to that in Remark 1.7: in the Frobenius manifold
![]() $\hat {H}_1$
, the variable
$\hat {H}_1$
, the variable
![]() $\epsilon $
appears in the potential F while
$\epsilon $
appears in the potential F while
![]() $\frac {\partial }{\partial \epsilon }$
is not involved in the product
$\frac {\partial }{\partial \epsilon }$
is not involved in the product
![]() $\star _t$
; in the F-manifold
$\star _t$
; in the F-manifold
![]() $\hat {H}_2$
, the variable
$\hat {H}_2$
, the variable
![]() $t^o$
does not appear in
$t^o$
does not appear in
![]() $\overline {F}$
while
$\overline {F}$
while
![]() $\frac {\partial }{\partial t^o}$
is involved in
$\frac {\partial }{\partial t^o}$
is involved in
![]() $\star _t$
. From a geometric point of view, we may view the open variable
$\star _t$
. From a geometric point of view, we may view the open variable
![]() $t^o$
as parameterizing a divisor-like insertion arising from the open sector. In
$t^o$
as parameterizing a divisor-like insertion arising from the open sector. In
![]() $\hat {H}_1$
, it contributes to the factor
$\hat {H}_1$
, it contributes to the factor
![]() $e^{t^o}\mathsf {X}_0$
appearing in the
$e^{t^o}\mathsf {X}_0$
appearing in the
![]() $F_{0,1}^{X,(L,f)}$
-part of F via the ‘open divisor equation’. However, in
$F_{0,1}^{X,(L,f)}$
-part of F via the ‘open divisor equation’. However, in
![]() $\hat {H}_2$
, the vector potential
$\hat {H}_2$
, the vector potential
![]() $\overline {F}$
defined by the restriction
$\overline {F}$
defined by the restriction
![]() $t^o = 0$
has no boundary insertions and does not depend on
$t^o = 0$
has no boundary insertions and does not depend on
![]() $t^o$
.
$t^o$
.
Despite the above differences, we will see that both structures
![]() $\hat {H}_1$
and
$\hat {H}_1$
and
![]() $\hat {H}_2$
can be viewed as extensions of the formal Frobenius manifold determined by
$\hat {H}_2$
can be viewed as extensions of the formal Frobenius manifold determined by
![]() $F_0^{X,T'}$
; see Remarks 5.7, 5.12.
$F_0^{X,T'}$
; see Remarks 5.7, 5.12.
1.3 Future works
1.3.1 Recursion for open Gromov-Witten invariants of toric Calabi-Yau 3-folds
In [Reference Kontsevich and Manin29], Kontsevich and Manin proved that closed Gromov-Witten invariants can be recursively computed from an initial set of known values. In particular, when X is Fano, this initial set of values is finite. A typical example is the recursive formula that calculates the Gromov-Witten invariants of
![]() $\mathbb {P}^2$
. This theorem is proved via the WDVV equations for closed Gromov-Witten invariants.
$\mathbb {P}^2$
. This theorem is proved via the WDVV equations for closed Gromov-Witten invariants.
In the study of open Gromov-Witten invariants, similar recursive formulas can be obtained via open WDVV equations. In many cases [Reference Chen and Zinger10, Reference Georgieva and Zinger19, Reference Hollands, Kosloff, Sela, Shu and Solomon25, Reference Horev and Solomon26, Reference Hugtenburg and Tukachinsky28, Reference Solomon and Tukachinsky43], open Gromov-Witten invariants have been shown to be computable from a finite initial set of values. Later in [Reference Blumberg and Tukachinsky6], a more general recursive formula is obtained based on a formal object called the Frobenius superpotential.
In our case, the open WDVV equations can be used to prove a recursive formula for open Gromov-Witten invariants of toric Calabi-Yau 3-folds. Since we study equivariant Gromov-Witten theory and our target spaces are Calabi-Yau, this recursive formula is more subtle and contains richer structures.
1.3.2 Open-closed map and variation of Hodge structures
In his ICM address, Kontsevich conjectured the homological mirror symmetry and moreover conjectured that this homological mirror symmetry implies enumerative mirror symmetry. Ganatra-Perutz-Sheridan [Reference Ganatra, Perutz and Sheridan18] show that for certain Calabi-Yaus, whose variations of Hodge structures are of Hodge-Tate type, the genus-zero Gromov-Witten invariants are indeed extractable from the Fukaya category. The strategy is to show that the open-closed map [Reference Fukaya, Oh, Ohta and Ono15, Reference Ganatra17] respects the variation of Hodge structures.
In [Reference Hugtenburg27], the open-closed map is extended to a map from the relative cyclic homology to the relative quantum homology whose definition is based on the open WDVV equations. In our case of toric Calabi-Yau 3-folds, the open WDVV equations studied in this paper may be used to construct relative quantum cohomology, which would further enable a study of the relative open-closed map and its compatibility with variations of Hodge structures.
1.4 Outline of the paper
In Section 2, we review the open geometry of
![]() $(X,L)$
and the corresponding closed geometry of
$(X,L)$
and the corresponding closed geometry of
![]() $\widetilde {X}$
. We will also study the equivariant cohomology of X and
$\widetilde {X}$
. We will also study the equivariant cohomology of X and
![]() $\widetilde {X}$
. In Section 3, we give the basic definitions of open and closed Gromov-Witten invariants for X and
$\widetilde {X}$
. In Section 3, we give the basic definitions of open and closed Gromov-Witten invariants for X and
![]() $\widetilde {X}$
, and then state the open/closed correspondence in Section 3.3. In Section 4, we review the WDVV equation in closed Gromov-Witten theory and use the specialization to
$\widetilde {X}$
, and then state the open/closed correspondence in Section 3.3. In Section 4, we review the WDVV equation in closed Gromov-Witten theory and use the specialization to
![]() $\widetilde {X}$
to prove non-linear partial differential equations which involve
$\widetilde {X}$
to prove non-linear partial differential equations which involve
![]() $F_0^{X,T'}$
and
$F_0^{X,T'}$
and
![]() $F_{0,1}^{X,(L,f)}$
. Finally, in Section 5, we use these equations to establish the main results of the paper on the formal Frobenius and F-manifold structures.
$F_{0,1}^{X,(L,f)}$
. Finally, in Section 5, we use these equations to establish the main results of the paper on the formal Frobenius and F-manifold structures.
2 Geometric setup
In this section, we review the geometry of toric Calabi-Yau 3-folds and Aganagic-Vafa branes. We then review the geometry of the corresponding toric Calabi-Yau 4-folds. We refer to [Reference Fang and Liu13, Reference Fang, Liu and Tseng14, Reference Liu and Yu33, Reference Liu and Yu34] for additional details. We work over
![]() $ {\mathbb {C}} $
.
$ {\mathbb {C}} $
.
2.1 Notations for toric geometry
In this paper, we use the following notations for an r-dimensional smooth toric variety Z defined by a fan
![]() $\Xi $
in
$\Xi $
in
![]() $\mathbb {R}^r$
. The algebraic torus of Z is isomorphic to
$\mathbb {R}^r$
. The algebraic torus of Z is isomorphic to
![]() $( {\mathbb {C}} ^{*})^r$
.
$( {\mathbb {C}} ^{*})^r$
.
-
• For
 $d = 0, \dots , r$
, let
$d = 0, \dots , r$
, let
 $\Xi (d)$
denote the set of d-dimensional cones in
$\Xi (d)$
denote the set of d-dimensional cones in
 $\Xi $
. For a cone
$\Xi $
. For a cone
 $\sigma \in \Xi (d)$
, let
$\sigma \in \Xi (d)$
, let
 $V(\sigma ) \subseteq Z$
denote the
$V(\sigma ) \subseteq Z$
denote the
 $( {\mathbb {C}} ^{*})^r$
-orbit closure corresponding to
$( {\mathbb {C}} ^{*})^r$
-orbit closure corresponding to
 $\sigma $
, which is a codimension-d closed subvariety of Z.
$\sigma $
, which is a codimension-d closed subvariety of Z. -
• For a maximal cone
 $\sigma \in \Xi (r)$
, let
$\sigma \in \Xi (r)$
, let
 $p_\sigma := V(\sigma )$
denote the corresponding
$p_\sigma := V(\sigma )$
denote the corresponding
 $( {\mathbb {C}} ^{*})^r$
-fixed point.
$( {\mathbb {C}} ^{*})^r$
-fixed point. -
• For a cone
 $\tau \in \Xi (r-1)$
, let
$\tau \in \Xi (r-1)$
, let
 $l_\tau := V(\tau )$
denote the corresponding
$l_\tau := V(\tau )$
denote the corresponding
 $( {\mathbb {C}} ^{*})^r$
-invariant line, which is isomorphic to either
$( {\mathbb {C}} ^{*})^r$
-invariant line, which is isomorphic to either
 $ {\mathbb {C}} $
or
$ {\mathbb {C}} $
or
 $\mathbb {P}^1$
. We set
$\mathbb {P}^1$
. We set
 $\Xi (r-1)_c := \{\tau \in \Xi (r-1): l_\tau \cong \mathbb {P}^1\}$
.
$\Xi (r-1)_c := \{\tau \in \Xi (r-1): l_\tau \cong \mathbb {P}^1\}$
. -
• Let
 $F(\Sigma ) := \{(\tau , \sigma ) \in \Xi (r-1) \times \Xi (r) : \tau \subset \sigma \}$
denote the set of flags in
$F(\Sigma ) := \{(\tau , \sigma ) \in \Xi (r-1) \times \Xi (r) : \tau \subset \sigma \}$
denote the set of flags in
 $\Xi $
.
$\Xi $
.
2.2 Open geometry
Let
![]() $N \cong \mathbb {Z}^3$
be a lattice and
$N \cong \mathbb {Z}^3$
be a lattice and
![]() $M := \mathrm {Hom}(N, \mathbb {Z})$
be the dual lattice. Let X be a smooth toric Calabi-Yau 3-fold specified by a finite fan
$M := \mathrm {Hom}(N, \mathbb {Z})$
be the dual lattice. Let X be a smooth toric Calabi-Yau 3-fold specified by a finite fan
![]() $\Sigma $
in
$\Sigma $
in
![]() $N_{\mathbb {R}} := N \otimes \mathbb {R} \cong \mathbb {R}^3$
. We assume that
$N_{\mathbb {R}} := N \otimes \mathbb {R} \cong \mathbb {R}^3$
. We assume that
![]() $\Sigma (3)$
is non-empty and every cone in
$\Sigma (3)$
is non-empty and every cone in
![]() $\Sigma $
is a face of some 3-cone.
$\Sigma $
is a face of some 3-cone.
Let
![]() $R := |\Sigma (1)|$
. Let
$R := |\Sigma (1)|$
. Let
![]() $\Sigma (1) = \{\rho _1, \dots , \rho _R\}$
be a listing of the rays in
$\Sigma (1) = \{\rho _1, \dots , \rho _R\}$
be a listing of the rays in
![]() $\Sigma $
, and for each
$\Sigma $
, and for each
![]() $i = 1, \dots , R$
let
$i = 1, \dots , R$
let
![]() $b_i \in N$
be the primitive generator of
$b_i \in N$
be the primitive generator of
![]() $\rho _i$
. The Calabi-Yau condition on X is equivalent to the existence of
$\rho _i$
. The Calabi-Yau condition on X is equivalent to the existence of
![]() $u_3 \in M$
such that
$u_3 \in M$
such that
![]() $\langle u_3, b_i \rangle = 1$
for all i, where
$\langle u_3, b_i \rangle = 1$
for all i, where
![]() $\langle -,- \rangle $
is the natural pairing between M and N. Let
$\langle -,- \rangle $
is the natural pairing between M and N. Let
![]() $N' := \ker (u_3: N \to \mathbb {Z}) \cong \mathbb {Z}^2$
.
$N' := \ker (u_3: N \to \mathbb {Z}) \cong \mathbb {Z}^2$
.
Let P be the cross-section of the support
![]() $|\Sigma |$
of
$|\Sigma |$
of
![]() $\Sigma $
in the hyperplane
$\Sigma $
in the hyperplane
which is a 2-dimensional lattice polytope with a triangulation induced by
![]() $\Sigma $
. We assume that P is simple. As in the setup of [Reference Liu and Yu33, Section 2.2], we do not assume that P is convex or equivalently X is semi-projective. There is a toric partial compactification
$\Sigma $
. We assume that P is simple. As in the setup of [Reference Liu and Yu33, Section 2.2], we do not assume that P is convex or equivalently X is semi-projective. There is a toric partial compactification
![]() $X \subseteq X'$
by a semi-projective smooth toric Calabi-Yau 3-fold
$X \subseteq X'$
by a semi-projective smooth toric Calabi-Yau 3-fold
![]() $X'$
determined by a fan
$X'$
determined by a fan
![]() $\Sigma '$
which contains
$\Sigma '$
which contains
![]() $\Sigma $
as a subfan and satisfies
$\Sigma $
as a subfan and satisfies
![]() $\Sigma '(1) = \Sigma (1)$
. The cross-section of
$\Sigma '(1) = \Sigma (1)$
. The cross-section of
![]() $\Sigma '$
with the hyperplane (2) is the convex hull
$\Sigma '$
with the hyperplane (2) is the convex hull
![]() $P'$
of P, and we have
$P'$
of P, and we have
![]() $P' \cap N = P \cap N = \{b_1, \dots , b_R\}$
.
$P' \cap N = P \cap N = \{b_1, \dots , b_R\}$
.
Let
![]() $T := N \otimes {\mathbb {C}} ^{*} \cong ( {\mathbb {C}} ^{*})^3$
be the algebraic torus of X, whose character lattice is
$T := N \otimes {\mathbb {C}} ^{*} \cong ( {\mathbb {C}} ^{*})^3$
be the algebraic torus of X, whose character lattice is
![]() $\mathrm {Hom}(T, {\mathbb {C}} ^{*}) \cong M$
. We consider a 2-subtorus
$\mathrm {Hom}(T, {\mathbb {C}} ^{*}) \cong M$
. We consider a 2-subtorus
![]() $T' := \ker (u_3: T \to {\mathbb {C}} ^{*}) = N' \otimes {\mathbb {C}} ^{*} \cong ( {\mathbb {C}} ^{*})^2$
. The fixed points and invariant lines of X under the
$T' := \ker (u_3: T \to {\mathbb {C}} ^{*}) = N' \otimes {\mathbb {C}} ^{*} \cong ( {\mathbb {C}} ^{*})^2$
. The fixed points and invariant lines of X under the
![]() $T'$
-action are the same as those under the T-action.
$T'$
-action are the same as those under the T-action.
Let
![]() $L \subset X$
be an Aganagic-Vafa brane in X, which is a Lagrangian submanifold diffeomorphic to
$L \subset X$
be an Aganagic-Vafa brane in X, which is a Lagrangian submanifold diffeomorphic to
![]() $S^1 \times {\mathbb {C}} $
. We refer to [Reference Fang and Liu13, Section 2.4], [Reference Liu and Yu33, Section 2.2] for detailed definitions. The brane L is invariant under the action of the maximal compact subtorus
$S^1 \times {\mathbb {C}} $
. We refer to [Reference Fang and Liu13, Section 2.4], [Reference Liu and Yu33, Section 2.2] for detailed definitions. The brane L is invariant under the action of the maximal compact subtorus
![]() $T_{\mathbb {R}}' \cong U(1)^2$
of
$T_{\mathbb {R}}' \cong U(1)^2$
of
![]() $T'$
. Moreover, it intersects a unique T-invariant line
$T'$
. Moreover, it intersects a unique T-invariant line
![]() $l_{\tau _0}$
in X, where
$l_{\tau _0}$
in X, where
![]() $\tau _0 \in \Sigma (2)$
. Given a semi-projective toric partial compactification
$\tau _0 \in \Sigma (2)$
. Given a semi-projective toric partial compactification
![]() $X'$
of X as above, L can be viewed as an Aganagic-Vafa brane in
$X'$
of X as above, L can be viewed as an Aganagic-Vafa brane in
![]() $X'$
, intersecting the T-invariant line in
$X'$
, intersecting the T-invariant line in
![]() $X'$
corresponding to
$X'$
corresponding to
![]() $\tau _0 \in \Sigma '(2)$
. As in [Reference Liu and Yu33, Assumption 2.3], we make the following assumption on L.
$\tau _0 \in \Sigma '(2)$
. As in [Reference Liu and Yu33, Assumption 2.3], we make the following assumption on L.
Assumption 2.1. We assume that L is an outer brane in the partial compactification
![]() $X'$
, that is,
$X'$
, that is,
![]() $\tau _0 \in \Sigma '(2) \setminus \Sigma '(2)_c$
.
$\tau _0 \in \Sigma '(2) \setminus \Sigma '(2)_c$
.
Note that this assumption does not depend on the choice of
![]() $X'$
. In particular,
$X'$
. In particular,
![]() $\tau _0 \in \Sigma (2) \setminus \Sigma (2)_c$
and L is also an outer brane in X. Let
$\tau _0 \in \Sigma (2) \setminus \Sigma (2)_c$
and L is also an outer brane in X. Let
![]() $\sigma _0 \in \Sigma (3)$
be the unique 3-cone containing
$\sigma _0 \in \Sigma (3)$
be the unique 3-cone containing
![]() $\tau _0$
as a face.
$\tau _0$
as a face.
For any cone
![]() $\sigma $
in
$\sigma $
in
![]() $\Sigma $
, we set
$\Sigma $
, we set
We assume without loss of generality that
with
![]() $b_1, b_2, b_3$
appearing in P in a counterclockwise order. Such labeling determines a unique way to complete
$b_1, b_2, b_3$
appearing in P in a counterclockwise order. Such labeling determines a unique way to complete
![]() $u_3$
into a
$u_3$
into a
![]() $\mathbb {Z}$
-basis
$\mathbb {Z}$
-basis
![]() $\{u_1, u_2, u_3\}$
of M such that under the dual
$\{u_1, u_2, u_3\}$
of M such that under the dual
![]() $\mathbb {Z}$
-basis
$\mathbb {Z}$
-basis
![]() $\{v_1, v_2, v_3\}$
of N, we have the coordinates
$\{v_1, v_2, v_3\}$
of N, we have the coordinates
For
![]() $i = 1, \dots , R$
, we write
$i = 1, \dots , R$
, we write
![]() $(m_i, n_i, 1)$
for the coordinate of
$(m_i, n_i, 1)$
for the coordinate of
![]() $b_i \in N$
under the basis
$b_i \in N$
under the basis
![]() $\{v_1, v_2, v_3\}$
. Assumption 2.1 implies that
$\{v_1, v_2, v_3\}$
. Assumption 2.1 implies that
![]() $m_i \ge 0$
for all i.
$m_i \ge 0$
for all i.
Finally, let
![]() $f \in \mathbb {Z}$
be a framing on the Aganagic-Vafa brane L. This determines a 1-subtorus
$f \in \mathbb {Z}$
be a framing on the Aganagic-Vafa brane L. This determines a 1-subtorus
![]() $T_f := \ker (u_2-fu_1: T' \to {\mathbb {C}} ^{*}) \subset T' \subset T$
. We take the following notations for the equivariant parameters of the tori:
$T_f := \ker (u_2-fu_1: T' \to {\mathbb {C}} ^{*}) \subset T' \subset T$
. We take the following notations for the equivariant parameters of the tori:
 $$ \begin{align*} & R_T := H^{*}_T(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3], && S_T:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3),\\ & R_{T'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2], && S_{T'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2),\\ & R_{T_f} := H^{*}_{T_f}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1], && S_{T_f}:= {\mathbb{C}} (\mathsf{u}_1). \end{align*} $$
$$ \begin{align*} & R_T := H^{*}_T(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3], && S_T:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3),\\ & R_{T'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2], && S_{T'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2),\\ & R_{T_f} := H^{*}_{T_f}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1], && S_{T_f}:= {\mathbb{C}} (\mathsf{u}_1). \end{align*} $$
Assumption 2.2. We assume that
![]() $f \in \mathbb {Z}$
is generic with respect to X (i.e., avoiding a finite subset of
$f \in \mathbb {Z}$
is generic with respect to X (i.e., avoiding a finite subset of
![]() $\mathbb {Z}$
depending on X).Footnote
2
$\mathbb {Z}$
depending on X).Footnote
2
2.3 Closed geometry
Under the open/closed correspondence [Reference Mayr38, Reference Liu and Yu33, Reference Liu and Yu34], the closed geometry corresponding to the open geometry
![]() $(X,L,f)$
is a smooth toric Calabi-Yau 4-fold
$(X,L,f)$
is a smooth toric Calabi-Yau 4-fold
![]() $\widetilde {X}$
that takes the form
$\widetilde {X}$
that takes the form
where
![]() $X \sqcup D$
is a toric partial compactification of X given by adding an additional toric divisor D corresponding to the ray generated by
$X \sqcup D$
is a toric partial compactification of X given by adding an additional toric divisor D corresponding to the ray generated by
![]() $(-1, -f, 0) \in N$
.Footnote
3
In
$(-1, -f, 0) \in N$
.Footnote
3
In
![]() $X \sqcup D$
, the T-invariant line
$X \sqcup D$
, the T-invariant line
![]() $l_{\tau _0} \cong {\mathbb {C}} $
that L intersects is compactified by an additional T-fixed point into a
$l_{\tau _0} \cong {\mathbb {C}} $
that L intersects is compactified by an additional T-fixed point into a
![]() $\mathbb {P}^1$
whose normal bundle is isomorphic to
$\mathbb {P}^1$
whose normal bundle is isomorphic to
![]() $\mathcal {O}_{\mathbb {P}^1}(f) \oplus \mathcal {O}_{\mathbb {P}^1}(-f-1)$
. There is an inclusion
$\mathcal {O}_{\mathbb {P}^1}(f) \oplus \mathcal {O}_{\mathbb {P}^1}(-f-1)$
. There is an inclusion
Let
![]() $\widetilde {N} := N \oplus \mathbb {Z} \cong \mathbb {Z}^4$
and
$\widetilde {N} := N \oplus \mathbb {Z} \cong \mathbb {Z}^4$
and
![]() $\widetilde {T} := \widetilde {N} \otimes {\mathbb {C}} ^{*} \cong ( {\mathbb {C}} ^{*})^4$
. We view N as a sublattice of
$\widetilde {T} := \widetilde {N} \otimes {\mathbb {C}} ^{*} \cong ( {\mathbb {C}} ^{*})^4$
. We view N as a sublattice of
![]() $\widetilde {N}$
and let
$\widetilde {N}$
and let
![]() $v_4$
be a generator of the additional
$v_4$
be a generator of the additional
![]() $\mathbb {Z}$
-component. The toric geometry of
$\mathbb {Z}$
-component. The toric geometry of
![]() $\widetilde {X}$
can be described by a fan
$\widetilde {X}$
can be described by a fan
![]() $\widetilde {\Sigma } \in \widetilde {N}_{\mathbb {R}} := \widetilde {N} \otimes \mathbb {R} \cong \mathbb {R}^4$
as follows. The rays of
$\widetilde {\Sigma } \in \widetilde {N}_{\mathbb {R}} := \widetilde {N} \otimes \mathbb {R} \cong \mathbb {R}^4$
as follows. The rays of
![]() $\widetilde {\Sigma }$
are given by
$\widetilde {\Sigma }$
are given by
where under the basis
![]() $\{v_1, \dots , v_4\}$
of
$\{v_1, \dots , v_4\}$
of
![]() $\widetilde {N}$
, the primitive generators
$\widetilde {N}$
, the primitive generators
![]() $\widetilde {b}_i \in \widetilde {N}$
of the rays
$\widetilde {b}_i \in \widetilde {N}$
of the rays
![]() $\widetilde {\rho }_i$
,
$\widetilde {\rho }_i$
,
![]() $i =1, \dots , R+2$
, have the following coordinates:
$i =1, \dots , R+2$
, have the following coordinates:
In
![]() $\widetilde {X} = \mathrm {Tot}(\mathcal {O}_{X \sqcup D}(-D))$
, the toric divisor
$\widetilde {X} = \mathrm {Tot}(\mathcal {O}_{X \sqcup D}(-D))$
, the toric divisor
![]() $V(\widetilde {\rho }_{R+1})$
is the restriction of the line bundle
$V(\widetilde {\rho }_{R+1})$
is the restriction of the line bundle
![]() $\mathcal {O}_{X \sqcup D}(-D)$
to D and
$\mathcal {O}_{X \sqcup D}(-D)$
to D and
![]() $V(\widetilde {\rho }_{R+2}) = X \sqcup D$
is the zero section.
$V(\widetilde {\rho }_{R+2}) = X \sqcup D$
is the zero section.
We describe cones
![]() $\widetilde {\sigma }$
in
$\widetilde {\sigma }$
in
![]() $\widetilde {\Sigma }$
by the index sets
$\widetilde {\Sigma }$
by the index sets
First,
![]() $\widetilde {\Sigma }$
contains
$\widetilde {\Sigma }$
contains
![]() $\Sigma $
as a subfan. Any cone
$\Sigma $
as a subfan. Any cone
![]() $\sigma \in \Sigma (d)$
,
$\sigma \in \Sigma (d)$
,
![]() $d = 0, \dots , 3$
, can be viewed as a cone in
$d = 0, \dots , 3$
, can be viewed as a cone in
![]() $\widetilde {\Sigma }(d)$
with
$\widetilde {\Sigma }(d)$
with
![]() $I^{\prime }_{\sigma }$
preserved, and there is a cone
$I^{\prime }_{\sigma }$
preserved, and there is a cone
![]() $\iota (\sigma ) \in \widetilde {\Sigma }(d+1)$
given by
$\iota (\sigma ) \in \widetilde {\Sigma }(d+1)$
given by
This induces an injective map
![]() $\iota : \Sigma (d) \to \widetilde {\Sigma }(d+1)$
.Footnote
4
For maximal cones in
$\iota : \Sigma (d) \to \widetilde {\Sigma }(d+1)$
.Footnote
4
For maximal cones in
![]() $\widetilde {\Sigma }$
, we have
$\widetilde {\Sigma }$
, we have
where the additional cone
![]() $\widetilde {\sigma }_0$
is characterized by
$\widetilde {\sigma }_0$
is characterized by
Note that
![]() $\widetilde {\sigma }_0$
is the only
$\widetilde {\sigma }_0$
is the only
![]() $4$
-cone that contains the ray
$4$
-cone that contains the ray
![]() $\widetilde {\rho }_{R+1}$
. Moreover, the map
$\widetilde {\rho }_{R+1}$
. Moreover, the map
![]() $\iota : \Sigma (2) \to \widetilde {\Sigma }(3)$
restricts to an injective map
$\iota : \Sigma (2) \to \widetilde {\Sigma }(3)$
restricts to an injective map
![]() $\iota : \Sigma (2)_c \to \widetilde {\Sigma }(3)_c$
, and we have
$\iota : \Sigma (2)_c \to \widetilde {\Sigma }(3)_c$
, and we have
Indeed, the
![]() $\widetilde {T}$
-invariant line
$\widetilde {T}$
-invariant line
![]() $l_{\iota (\tau _0)} \cong \mathbb {P}^1$
is the compactification of
$l_{\iota (\tau _0)} \cong \mathbb {P}^1$
is the compactification of
![]() $l_{\tau _0} \cong {\mathbb {C}} \subset X$
described at the beginning of this subsection.
$l_{\tau _0} \cong {\mathbb {C}} \subset X$
described at the beginning of this subsection.
Let
![]() $\widetilde {M} := \mathrm {Hom}(\widetilde {N}, \mathbb {Z})$
, which is the character lattice of the 4-torus
$\widetilde {M} := \mathrm {Hom}(\widetilde {N}, \mathbb {Z})$
, which is the character lattice of the 4-torus
![]() $\widetilde {T}$
, and
$\widetilde {T}$
, and
![]() $\{u_1, \dots , u_4\}$
be the basis of
$\{u_1, \dots , u_4\}$
be the basis of
![]() $\widetilde {M}$
dual to the basis
$\widetilde {M}$
dual to the basis
![]() $\{v_1, \dots , v_4\}$
of
$\{v_1, \dots , v_4\}$
of
![]() $\widetilde {N}$
. Here, we abuse notations since
$\widetilde {N}$
. Here, we abuse notations since
![]() $u_1, u_2, u_3 \in \widetilde {M}$
are natural lifts of the corresponding elements of M defined before under the projection
$u_1, u_2, u_3 \in \widetilde {M}$
are natural lifts of the corresponding elements of M defined before under the projection
![]() $\widetilde {M} \to M$
. We consider a 3-subtorus
$\widetilde {M} \to M$
. We consider a 3-subtorus
![]() $\widetilde {T}':= \ker (u_3: \widetilde {T} \to {\mathbb {C}} ^{*}) \cong ( {\mathbb {C}} ^{*})^3$
of
$\widetilde {T}':= \ker (u_3: \widetilde {T} \to {\mathbb {C}} ^{*}) \cong ( {\mathbb {C}} ^{*})^3$
of
![]() $\widetilde {T}$
, which contains
$\widetilde {T}$
, which contains
![]() $T'$
and
$T'$
and
![]() $T_f$
as subtori. The fixed points and invariant lines of
$T_f$
as subtori. The fixed points and invariant lines of
![]() $\widetilde {X}$
under the
$\widetilde {X}$
under the
![]() $\widetilde {T}'$
-action are the same as those under the
$\widetilde {T}'$
-action are the same as those under the
![]() $\widetilde {T}$
-action. We introduce the following notations:
$\widetilde {T}$
-action. We introduce the following notations:
 $$ \begin{align*} & R_{\widetilde{T}} := H^{*}_T(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3, \mathsf{u}_4], && S_{\widetilde{T}}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3, \mathsf{u}_4),\\ & R_{\widetilde{T}'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4], && S_{\widetilde{T}'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4). \end{align*} $$
$$ \begin{align*} & R_{\widetilde{T}} := H^{*}_T(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3, \mathsf{u}_4], && S_{\widetilde{T}}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_3, \mathsf{u}_4),\\ & R_{\widetilde{T}'} := H^{*}_{T'}(\mathrm{pt}) = {\mathbb{C}} [\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4], && S_{\widetilde{T}'}:= {\mathbb{C}} (\mathsf{u}_1, \mathsf{u}_2, \mathsf{u}_4). \end{align*} $$
2.4 Second homology and effective curve classes
The intersection of L with
![]() $l_{\tau _0} \cong {\mathbb {C}} $
in X is isomorphic to
$l_{\tau _0} \cong {\mathbb {C}} $
in X is isomorphic to
![]() $S^1$
and bounds a holomorphic disk B in
$S^1$
and bounds a holomorphic disk B in
![]() $l_{\tau _0}$
, oriented by the holomorphic structure of X. The disk B represents a class
$l_{\tau _0}$
, oriented by the holomorphic structure of X. The disk B represents a class
![]() $[B]$
in
$[B]$
in
![]() $H_2(X, L; \mathbb {Z})$
, and its boundary
$H_2(X, L; \mathbb {Z})$
, and its boundary
![]() $\partial B = L \cap l_{\tau _0}$
generates
$\partial B = L \cap l_{\tau _0}$
generates
![]() $H_1(L; \mathbb {Z}) \cong \mathbb {Z}[\partial B]$
. We have a splitting
$H_1(L; \mathbb {Z}) \cong \mathbb {Z}[\partial B]$
. We have a splitting
We introduce the following notations for the semigroups of effective classes:
 $$ \begin{align} \begin{aligned} & E(X) := {\mathrm{NE}}(X) \cap H_2(X; \mathbb{Z}),\\ & E(X, L) := E(X) \oplus \mathbb{Z}_{\ge 0} [B] \subset H_2(X, L; \mathbb{Z}),\\ & E(\widetilde{X}) := {\mathrm{NE}}(\widetilde{X}) \cap H_2(\widetilde{X}; \mathbb{Z}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & E(X) := {\mathrm{NE}}(X) \cap H_2(X; \mathbb{Z}),\\ & E(X, L) := E(X) \oplus \mathbb{Z}_{\ge 0} [B] \subset H_2(X, L; \mathbb{Z}),\\ & E(\widetilde{X}) := {\mathrm{NE}}(\widetilde{X}) \cap H_2(\widetilde{X}; \mathbb{Z}). \end{aligned} \end{align} $$
The inclusion
![]() $\iota : X \to \widetilde {X}$
induces an isomorphism
$\iota : X \to \widetilde {X}$
induces an isomorphism
which restricts to a semigroup isomorphism
We will thus use the coordinates
![]() $(\beta , d) \in E(X) \oplus \mathbb {Z}_{\ge 0}$
for both semigroups above. The pairing between
$(\beta , d) \in E(X) \oplus \mathbb {Z}_{\ge 0}$
for both semigroups above. The pairing between
![]() $\widetilde {\beta } = (\beta , d) \in E(\widetilde {X})$
and the divisor class
$\widetilde {\beta } = (\beta , d) \in E(\widetilde {X})$
and the divisor class
![]() $[V(\widetilde {\rho }_{R+1})]$
is
$[V(\widetilde {\rho }_{R+1})]$
is
2.5 Flags and tangent weights at torus-fixed points
For a flag
![]() $(\tau , \sigma ) \in F(\Sigma )$
, let
$(\tau , \sigma ) \in F(\Sigma )$
, let
be the weight of the
![]() $T'$
-action on tangent space
$T'$
-action on tangent space
![]() $T_{p_\sigma }l_{\tau }$
of
$T_{p_\sigma }l_{\tau }$
of
![]() $l_{\tau }$
at
$l_{\tau }$
at
![]() $p_{\sigma }$
. Similarly, for a flag
$p_{\sigma }$
. Similarly, for a flag
![]() $(\widetilde {\tau }, \widetilde {\sigma }) \in F(\widetilde {\Sigma })$
, let
$(\widetilde {\tau }, \widetilde {\sigma }) \in F(\widetilde {\Sigma })$
, let
The maps
![]() $\iota : \Sigma (d) \to \widetilde {\Sigma }(d+1)$
defined in Section 2.3 induce an injective map
$\iota : \Sigma (d) \to \widetilde {\Sigma }(d+1)$
defined in Section 2.3 induce an injective map
![]() $\iota : F(\Sigma ) \to F(\widetilde {\Sigma })$
,
$\iota : F(\Sigma ) \to F(\widetilde {\Sigma })$
,
![]() $(\tau , \sigma ) \mapsto (\iota (\tau ), \iota (\sigma ))$
. We have
$(\tau , \sigma ) \mapsto (\iota (\tau ), \iota (\sigma ))$
. We have
Each 4-cone
![]() $\iota (\sigma ) \in \widetilde {\Sigma }(4)$
with
$\iota (\sigma ) \in \widetilde {\Sigma }(4)$
with
![]() $\sigma \in \Sigma (3) \subset \widetilde {\Sigma }(3)$
belongs to an additional flag
$\sigma \in \Sigma (3) \subset \widetilde {\Sigma }(3)$
belongs to an additional flag
![]() $(\sigma , \iota (\sigma )) \in F(\widetilde {\Sigma })$
. We have
$(\sigma , \iota (\sigma )) \in F(\widetilde {\Sigma })$
. We have
The additional 4-cone
![]() $\widetilde {\sigma }_0 \in \widetilde {\Sigma }(4) \setminus \iota (\Sigma (3))$
belongs to the flags
$\widetilde {\sigma }_0 \in \widetilde {\Sigma }(4) \setminus \iota (\Sigma (3))$
belongs to the flags
where the facets
![]() $\widetilde {\tau }_2, \widetilde {\tau }_3, \widetilde {\tau }_4$
of
$\widetilde {\tau }_2, \widetilde {\tau }_3, \widetilde {\tau }_4$
of
![]() $\widetilde {\sigma }_0$
are given by
$\widetilde {\sigma }_0$
are given by
The tangent weights are given by
2.6 Equivariant cohomology and bases
We fix an ordering of the
![]() $T'$
-fixed points of X by
$T'$
-fixed points of X by
and denote the corresponding
![]() $\widetilde {T}'$
-fixed points of
$\widetilde {T}'$
-fixed points of
![]() $\widetilde {X}$
by
$\widetilde {X}$
by
We denote the additional
![]() $\widetilde {T}'$
-fixed point
$\widetilde {T}'$
-fixed point
![]() $p_{\widetilde {\sigma }_0}$
of
$p_{\widetilde {\sigma }_0}$
of
![]() $\widetilde {X}$
by
$\widetilde {X}$
by
![]() $\widetilde {p}_{m+1}$
.
$\widetilde {p}_{m+1}$
.
We consider the basis
![]() $\{\phi _1,\dots ,\phi _m\}$
of
$\{\phi _1,\dots ,\phi _m\}$
of
![]() $H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
defined as
$H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
defined as
Then for
![]() $i, j = 1, \dots , m$
, we have
$i, j = 1, \dots , m$
, we have
where
![]() $(-,-)_{X, T'}$
is the
$(-,-)_{X, T'}$
is the
![]() $T'$
-equivariant Poincaré pairing on X. It follows that
$T'$
-equivariant Poincaré pairing on X. It follows that
![]() $\{\phi _1,\dots ,\phi _m\}$
is a canonical basis of the semi-simple Frobenius algebra
$\{\phi _1,\dots ,\phi _m\}$
is a canonical basis of the semi-simple Frobenius algebra
Similarly, we define the basis
![]() $\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m,\widetilde {\phi }_{m+1} \}$
of
$\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m,\widetilde {\phi }_{m+1} \}$
of
![]() $H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
as
$H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
as
 $$ \begin{align*}\widetilde{\phi}_i := \frac{[\widetilde{p}_i]}{e_{\widetilde{T}'}(T_{\widetilde{p}_i}\widetilde{X})} = \frac{[\widetilde{p}_i]}{\Delta^{i,\widetilde{T}'}},\qquad \Delta^{i,\widetilde{T}'} := e_{\widetilde{T}'}(T_{\widetilde{p}_i}\widetilde{X}). \end{align*} $$
$$ \begin{align*}\widetilde{\phi}_i := \frac{[\widetilde{p}_i]}{e_{\widetilde{T}'}(T_{\widetilde{p}_i}\widetilde{X})} = \frac{[\widetilde{p}_i]}{\Delta^{i,\widetilde{T}'}},\qquad \Delta^{i,\widetilde{T}'} := e_{\widetilde{T}'}(T_{\widetilde{p}_i}\widetilde{X}). \end{align*} $$
Note that for any
![]() $i, j = 1, \dots , m$
, we have
$i, j = 1, \dots , m$
, we have
and
For
![]() $i, j = 1, \dots , m+1$
, we have
$i, j = 1, \dots , m+1$
, we have
where
![]() $(-,-)_{\widetilde {X}, \widetilde {T}'}$
is the
$(-,-)_{\widetilde {X}, \widetilde {T}'}$
is the
![]() $\widetilde {T}'$
-equivariant Poincaré pairing on
$\widetilde {T}'$
-equivariant Poincaré pairing on
![]() $\widetilde {X}$
. It follows that
$\widetilde {X}$
. It follows that
![]() $\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_{m+1}\}$
is a canonical basis of the semi-simple Frobenius algebra
$\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_{m+1}\}$
is a canonical basis of the semi-simple Frobenius algebra
Moreover, for
![]() $i = 1, \dots , R+2$
, let
$i = 1, \dots , R+2$
, let
denote the
![]() $\widetilde {T}'$
-equivariant Poincaré dual of the divisor
$\widetilde {T}'$
-equivariant Poincaré dual of the divisor
![]() $V(\widetilde {\rho }_i)$
. Specifically, we denote
$V(\widetilde {\rho }_i)$
. Specifically, we denote
Since the divisor
![]() $V(\widetilde {\rho }_{R+1})$
only contains the
$V(\widetilde {\rho }_{R+1})$
only contains the
![]() $\widetilde {T}'$
-fixed point
$\widetilde {T}'$
-fixed point
![]() $p_{\widetilde {\sigma }_0} = \widetilde {p}_{m+1}$
, we have that
$p_{\widetilde {\sigma }_0} = \widetilde {p}_{m+1}$
, we have that
3 Gromov-Witten theory and open/closed correspondence
In this section, we review the different types of Gromov-Witten invariants involved in our study of Frobenius structures, specifically the closed invariants of X and
![]() $\widetilde {X}$
as well as the open invariants of
$\widetilde {X}$
as well as the open invariants of
![]() $(X, L)$
. We then use the open/closed correspondence [Reference Liu and Yu33, Reference Liu and Yu34] to obtain a refined relation among the generating functions of Gromov-Witten invariants (Theorem 3.1).
$(X, L)$
. We then use the open/closed correspondence [Reference Liu and Yu33, Reference Liu and Yu34] to obtain a refined relation among the generating functions of Gromov-Witten invariants (Theorem 3.1).
3.1 Closed Gromov-Witten invariants of X and
 $\widetilde {X}$
$\widetilde {X}$
We refer to [Reference Liu32] for additional details on virtual localization [Reference Graber and Pandharipande22] in the Gromov-Witten theory of toric varieties.
For
![]() $n \in \mathbb {Z}_{\ge 0}$
and effective class
$n \in \mathbb {Z}_{\ge 0}$
and effective class
![]() $\beta \in E(X)$
(see (3)), let
$\beta \in E(X)$
(see (3)), let
![]() $\overline {\mathcal {M}}_{0,n}(X, \beta )$
be the moduli space of genus-zero, n-pointed, degree-
$\overline {\mathcal {M}}_{0,n}(X, \beta )$
be the moduli space of genus-zero, n-pointed, degree-
![]() $\beta $
stable maps to X. Given
$\beta $
stable maps to X. Given
![]() $T'$
-equivariant cohomology classes
$T'$
-equivariant cohomology classes
![]() $\gamma _1, \dots , \gamma _n \in H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
as insertions, we define the closed Gromov-Witten invariant
$\gamma _1, \dots , \gamma _n \in H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
as insertions, we define the closed Gromov-Witten invariant
 $$ \begin{align*}\langle \gamma_1, \dots, \gamma_n \rangle^{X, T'}_{0,n,\beta} := \int_{[\overline{\mathcal{M}}_{0,n}(X, \beta)^{T'}]^{ {\mathrm{vir}} }} \frac{\prod_{i=1}^n \mathrm{ev}_i^{*}(\gamma_i)}{e_{T'}(N^{ {\mathrm{vir}} })} \qquad \in S_{T'} \end{align*} $$
$$ \begin{align*}\langle \gamma_1, \dots, \gamma_n \rangle^{X, T'}_{0,n,\beta} := \int_{[\overline{\mathcal{M}}_{0,n}(X, \beta)^{T'}]^{ {\mathrm{vir}} }} \frac{\prod_{i=1}^n \mathrm{ev}_i^{*}(\gamma_i)}{e_{T'}(N^{ {\mathrm{vir}} })} \qquad \in S_{T'} \end{align*} $$
by localization with respect to the torus
![]() $T'$
, where for
$T'$
, where for
![]() $i = 1, \dots , n$
,
$i = 1, \dots , n$
,
![]() $\mathrm {ev}_i: \overline {\mathcal {M}}_{0,n}(X, \beta ) \to X$
is the evaluation map at the i-th marked point.
$\mathrm {ev}_i: \overline {\mathcal {M}}_{0,n}(X, \beta ) \to X$
is the evaluation map at the i-th marked point.
We now define a generating function of such invariants. The Novikov ring of X is the completion of the semigroup ring of
![]() $E(X)$
,
$E(X)$
,
 $$ \begin{align*}\Lambda_X := \left\{\sum_{\beta \in E(X)} c_\beta Q^\beta : c_\beta \in {\mathbb{C}} \right\}, \end{align*} $$
$$ \begin{align*}\Lambda_X := \left\{\sum_{\beta \in E(X)} c_\beta Q^\beta : c_\beta \in {\mathbb{C}} \right\}, \end{align*} $$
in which we use
![]() $Q^\beta $
to denote the semigroup ring element corresponding to
$Q^\beta $
to denote the semigroup ring element corresponding to
![]() $\beta \in E(X)$
. We will also use the equivariant versions
$\beta \in E(X)$
. We will also use the equivariant versions
Consider the basis
![]() $\{\phi _1,\dots ,\phi _m\}$
of
$\{\phi _1,\dots ,\phi _m\}$
of
![]() $H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
defined in Section 2.6. Let
$H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
defined in Section 2.6. Let
 $$ \begin{align*}t := \sum_{i=1}^m t^i \phi_i, \end{align*} $$
$$ \begin{align*}t := \sum_{i=1}^m t^i \phi_i, \end{align*} $$
where
![]() $t^1, \dots , t^m$
are formal variables viewed as coordinates. The genus-zero,
$t^1, \dots , t^m$
are formal variables viewed as coordinates. The genus-zero,
![]() $T'$
-equivariant Gromov-Witten potential of X is the following generating function of closed Gromov-Witten invariants:
$T'$
-equivariant Gromov-Witten potential of X is the following generating function of closed Gromov-Witten invariants:

Now we set up a parallel theory for
![]() $\widetilde {X}$
. For
$\widetilde {X}$
. For
![]() $n \in \mathbb {Z}_{\ge 0}$
and effective class
$n \in \mathbb {Z}_{\ge 0}$
and effective class
![]() $\widetilde {\beta } \in E(\widetilde {X})$
(see (3)), let
$\widetilde {\beta } \in E(\widetilde {X})$
(see (3)), let
![]() $\overline {\mathcal {M}}_{0,n}(\widetilde {X}, \widetilde {\beta })$
be the moduli space of genus-zero, n-pointed, degree-
$\overline {\mathcal {M}}_{0,n}(\widetilde {X}, \widetilde {\beta })$
be the moduli space of genus-zero, n-pointed, degree-
![]() $\widetilde {\beta }$
stable maps to
$\widetilde {\beta }$
stable maps to
![]() $\widetilde {X}$
. Given
$\widetilde {X}$
. Given
![]() $\widetilde {T}'$
-equivariant cohomology classes
$\widetilde {T}'$
-equivariant cohomology classes
![]() $\widetilde {\gamma }_1, \dots , \widetilde {\gamma }_n \in H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
as insertions, we define the closed Gromov-Witten invariant
$\widetilde {\gamma }_1, \dots , \widetilde {\gamma }_n \in H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
as insertions, we define the closed Gromov-Witten invariant
 $$ \begin{align*}\langle \widetilde{\gamma}_1, \dots, \widetilde{\gamma}_n \rangle^{\widetilde{X}, \widetilde{T}'}_{0,n,\widetilde{\beta}} := \int_{[\overline{\mathcal{M}}_{0,n}(\widetilde{X}, \widetilde{\beta})^{\widetilde{T}'}]^{ {\mathrm{vir}} }} \frac{\prod_{i=1}^n \mathrm{ev}_i^{*}(\widetilde{\gamma}_i)}{e_{\widetilde{T}'}(N^{ {\mathrm{vir}} })} \qquad \in S_{\widetilde{T}'} \end{align*} $$
$$ \begin{align*}\langle \widetilde{\gamma}_1, \dots, \widetilde{\gamma}_n \rangle^{\widetilde{X}, \widetilde{T}'}_{0,n,\widetilde{\beta}} := \int_{[\overline{\mathcal{M}}_{0,n}(\widetilde{X}, \widetilde{\beta})^{\widetilde{T}'}]^{ {\mathrm{vir}} }} \frac{\prod_{i=1}^n \mathrm{ev}_i^{*}(\widetilde{\gamma}_i)}{e_{\widetilde{T}'}(N^{ {\mathrm{vir}} })} \qquad \in S_{\widetilde{T}'} \end{align*} $$
by localization with respect to the torus
![]() $\widetilde {T}'$
, where for
$\widetilde {T}'$
, where for
![]() $i = 1, \dots , n$
,
$i = 1, \dots , n$
,
![]() $\mathrm {ev}_i: \overline {\mathcal {M}}_{0,n}(\widetilde {X}, \widetilde {\beta }) \to \widetilde {X}$
is the evaluation map at the i-th marked point.
$\mathrm {ev}_i: \overline {\mathcal {M}}_{0,n}(\widetilde {X}, \widetilde {\beta }) \to \widetilde {X}$
is the evaluation map at the i-th marked point.
The Novikov ring of
![]() $\widetilde {X}$
is the completion of the semigroup ring of
$\widetilde {X}$
is the completion of the semigroup ring of
![]() $E(\widetilde {X})$
,
$E(\widetilde {X})$
,
 $$ \begin{align*}\Lambda_{\widetilde{X}} := \left\{\sum_{\widetilde{\beta} \in E(\widetilde{X})} c_{\widetilde{\beta}} \widetilde{Q}^{\widetilde{\beta}} : c_{\widetilde{\beta}} \in {\mathbb{C}} \right\}, \end{align*} $$
$$ \begin{align*}\Lambda_{\widetilde{X}} := \left\{\sum_{\widetilde{\beta} \in E(\widetilde{X})} c_{\widetilde{\beta}} \widetilde{Q}^{\widetilde{\beta}} : c_{\widetilde{\beta}} \in {\mathbb{C}} \right\}, \end{align*} $$
in which we use
![]() $\widetilde {Q}^{\widetilde {\beta }}$
to denote the semigroup ring element corresponding to
$\widetilde {Q}^{\widetilde {\beta }}$
to denote the semigroup ring element corresponding to
![]() $\widetilde {\beta } \in E(\widetilde {X})$
. We will also use the equivariant version
$\widetilde {\beta } \in E(\widetilde {X})$
. We will also use the equivariant version
Consider the basis
![]() $\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m, \widetilde {\phi }_{m+1}\}$
of
$\{\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m, \widetilde {\phi }_{m+1}\}$
of
![]() $H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
defined in Section 2.6. Let
$H^{*}_{\widetilde {T}'}(\widetilde {X}) \otimes _{R_{\widetilde {T}'}} S_{\widetilde {T}'}$
defined in Section 2.6. Let
 $$ \begin{align*}\tilde{t} := \sum_{i=1}^m t^i \widetilde{\phi}_i, \qquad \hat{t} := \tilde{t} + t^{m+1}\widetilde{\phi}_{m+1}, \end{align*} $$
$$ \begin{align*}\tilde{t} := \sum_{i=1}^m t^i \widetilde{\phi}_i, \qquad \hat{t} := \tilde{t} + t^{m+1}\widetilde{\phi}_{m+1}, \end{align*} $$
where
![]() $t^1, \dots , t^m$
are formal variables as before and
$t^1, \dots , t^m$
are formal variables as before and
![]() $t^{m+1}$
is an additional formal variable. The genus-zero,
$t^{m+1}$
is an additional formal variable. The genus-zero,
![]() $\widetilde {T}'$
-equivariant Gromov-Witten potential of
$\widetilde {T}'$
-equivariant Gromov-Witten potential of
![]() $\widetilde {X}$
is the following generating functions of closed Gromov-Witten invariants:
$\widetilde {X}$
is the following generating functions of closed Gromov-Witten invariants:

By (6), we have
 $$ \begin{align*}\hat{t} = \tilde{t} - \frac{t^{m+1}}{\mathsf{u}_1}\widetilde{D}. \end{align*} $$
$$ \begin{align*}\hat{t} = \tilde{t} - \frac{t^{m+1}}{\mathsf{u}_1}\widetilde{D}. \end{align*} $$
Recall from Section 2.4 that each
![]() $\widetilde {\beta } \in E(\widetilde {X})$
can be uniquely expressed as
$\widetilde {\beta } \in E(\widetilde {X})$
can be uniquely expressed as
![]() $\iota _*(\beta ) + d[l_{\iota (\tau _0)}]$
for some
$\iota _*(\beta ) + d[l_{\iota (\tau _0)}]$
for some
![]() $\beta \in E(X)$
and
$\beta \in E(X)$
and
![]() $d \in \mathbb {Z}_{\ge 0}$
. The divisor equation then implies that
$d \in \mathbb {Z}_{\ge 0}$
. The divisor equation then implies that
 $$ \begin{align} & F_0^{\widetilde{X},\widetilde{T}'}(t^1, \dots, t^m, t^{m+1}) \nonumber \\ &\quad = \frac{(t^{m+1})^3}{6\Delta^{m+1,\widetilde{T}'}} + \sum_{\widetilde{\beta} = (\beta, d) \in E(\widetilde{X})} \sum_{n \in \mathbb{Z}_{\ge 0}} \frac{\langle \tilde{t}, \dots, \tilde{t} \rangle^{\widetilde{X}, \widetilde{T}'}_{0,n,\widetilde{\beta}}}{n!}\widetilde{Q}^{\iota_*(\beta)}\left(e^{-\frac{t^{m+1}}{\mathsf{u}_1}} \widetilde{Q}^{[l_{\iota(\tau_0)}]} \right)^d. \end{align} $$
$$ \begin{align} & F_0^{\widetilde{X},\widetilde{T}'}(t^1, \dots, t^m, t^{m+1}) \nonumber \\ &\quad = \frac{(t^{m+1})^3}{6\Delta^{m+1,\widetilde{T}'}} + \sum_{\widetilde{\beta} = (\beta, d) \in E(\widetilde{X})} \sum_{n \in \mathbb{Z}_{\ge 0}} \frac{\langle \tilde{t}, \dots, \tilde{t} \rangle^{\widetilde{X}, \widetilde{T}'}_{0,n,\widetilde{\beta}}}{n!}\widetilde{Q}^{\iota_*(\beta)}\left(e^{-\frac{t^{m+1}}{\mathsf{u}_1}} \widetilde{Q}^{[l_{\iota(\tau_0)}]} \right)^d. \end{align} $$
Here, the term
![]() $\frac {(t^{m+1})^3}{6\Delta ^{m+1,\widetilde {T}'}}$
captures the
$\frac {(t^{m+1})^3}{6\Delta ^{m+1,\widetilde {T}'}}$
captures the
![]() $t^{m+1}$
-dependence of the (3-pointed) degree-
$t^{m+1}$
-dependence of the (3-pointed) degree-
![]() $0$
invariants in
$0$
invariants in
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
:
$F_0^{\widetilde {X},\widetilde {T}'}$
:
 $$ \begin{align*}\frac{\langle t^{m+1}\widetilde{\phi}_{m+1}, t^{m+1}\widetilde{\phi}_{m+1}, t^{m+1}\widetilde{\phi}_{m+1} \rangle^{\widetilde{X}, \widetilde{T}'}_{0,3,0}}{3!} = \frac{(t^{m+1})^3}{6} (\widetilde{\phi}_{m+1} \cup \widetilde{\phi}_{m+1},\widetilde{\phi}_{m+1})_{\widetilde{X},\widetilde{T}'} = \frac{(t^{m+1})^3}{6\Delta^{m+1,\widetilde{T}'}}. \end{align*} $$
$$ \begin{align*}\frac{\langle t^{m+1}\widetilde{\phi}_{m+1}, t^{m+1}\widetilde{\phi}_{m+1}, t^{m+1}\widetilde{\phi}_{m+1} \rangle^{\widetilde{X}, \widetilde{T}'}_{0,3,0}}{3!} = \frac{(t^{m+1})^3}{6} (\widetilde{\phi}_{m+1} \cup \widetilde{\phi}_{m+1},\widetilde{\phi}_{m+1})_{\widetilde{X},\widetilde{T}'} = \frac{(t^{m+1})^3}{6\Delta^{m+1,\widetilde{T}'}}. \end{align*} $$
Note that
![]() $\widetilde {\phi }_i \cup \widetilde {\phi }_{m+1} = 0$
for any
$\widetilde {\phi }_i \cup \widetilde {\phi }_{m+1} = 0$
for any
![]() $i = 1, \dots , m$
.
$i = 1, \dots , m$
.
3.2 Open Gromov-Witten invariants of
 $(X, L, f)$
$(X, L, f)$
Recall from Section 2.2 that the
![]() $T^{\prime }_{\mathbb {R}}$
-action on X preserves the Lagrangian L and may thus be used to define open Gromov-Witten invariants, specifically disk invariants which are virtual counts of open stable maps from genus-zero domains with one boundary component. We now recall the definitions and refer to [Reference Fang and Liu13, Reference Fang, Liu and Tseng14] for additional details.
$T^{\prime }_{\mathbb {R}}$
-action on X preserves the Lagrangian L and may thus be used to define open Gromov-Witten invariants, specifically disk invariants which are virtual counts of open stable maps from genus-zero domains with one boundary component. We now recall the definitions and refer to [Reference Fang and Liu13, Reference Fang, Liu and Tseng14] for additional details.
For
![]() $n \in \mathbb {Z}_{\ge 0}$
and effective class
$n \in \mathbb {Z}_{\ge 0}$
and effective class
![]() $\beta ' = (\beta , d) \in E(X, L)$
(see (3)) with
$\beta ' = (\beta , d) \in E(X, L)$
(see (3)) with
![]() $d \in \mathbb {Z}_{>0}$
, let
$d \in \mathbb {Z}_{>0}$
, let
![]() $\overline {\mathcal {M}}_{(0,1),n}(X,L \mid \beta ', d)$
be the moduli space of degree-
$\overline {\mathcal {M}}_{(0,1),n}(X,L \mid \beta ', d)$
be the moduli space of degree-
![]() $\beta '$
stable maps to
$\beta '$
stable maps to
![]() $(X,L)$
from domains
$(X,L)$
from domains
![]() $(C, \partial C)$
with
$(C, \partial C)$
with
-
• topological type
 $(0,1)$
, i.e. C is a nodal Riemann surface of arithmetic genus zero with one open disk removed, and
$(0,1)$
, i.e. C is a nodal Riemann surface of arithmetic genus zero with one open disk removed, and -
• n interior marked points disjoint from
 $\partial C$
.
$\partial C$
.
Given
![]() $T'$
-equivariant (or equivalently
$T'$
-equivariant (or equivalently
![]() $T^{\prime }_{\mathbb {R}}$
-equivariant) cohomology classes
$T^{\prime }_{\mathbb {R}}$
-equivariant) cohomology classes
![]() $\gamma _1, \dots , \gamma _n \in H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
as insertions, we define the disk invariant
$\gamma _1, \dots , \gamma _n \in H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
as insertions, we define the disk invariant
 $$ \begin{align*}\langle \gamma_1, \dots, \gamma_n \rangle^{X, L}_{(0,1),n,\beta', d} := \int_{[\overline{\mathcal{M}}_{(0,1),n}(X,L \mid \beta', d)^{T^{\prime}_{\mathbb{R}}}]^{ {\mathrm{vir}} }} \frac{\prod_{i=1}^n \mathrm{ev}_i^{*}(\gamma_i)}{e_{T^{\prime}_{\mathbb{R}}}(N^{ {\mathrm{vir}} })} \qquad \in S_{T'} \end{align*} $$
$$ \begin{align*}\langle \gamma_1, \dots, \gamma_n \rangle^{X, L}_{(0,1),n,\beta', d} := \int_{[\overline{\mathcal{M}}_{(0,1),n}(X,L \mid \beta', d)^{T^{\prime}_{\mathbb{R}}}]^{ {\mathrm{vir}} }} \frac{\prod_{i=1}^n \mathrm{ev}_i^{*}(\gamma_i)}{e_{T^{\prime}_{\mathbb{R}}}(N^{ {\mathrm{vir}} })} \qquad \in S_{T'} \end{align*} $$
by localization with respect to the compact torus
![]() $T^{\prime }_{\mathbb {R}}$
, where for
$T^{\prime }_{\mathbb {R}}$
, where for
![]() $i = 1, \dots , n$
,
$i = 1, \dots , n$
,
![]() $\mathrm {ev}_i: \overline {\mathcal {M}}_{(0,1),n}(X,L \mid \beta ', d) \to X$
is the evaluation map at the i-th marked point. Here, we identify the field of fractions of
$\mathrm {ev}_i: \overline {\mathcal {M}}_{(0,1),n}(X,L \mid \beta ', d) \to X$
is the evaluation map at the i-th marked point. Here, we identify the field of fractions of
![]() $H^{*}_{T^{\prime }_{\mathbb {R}}}(\mathrm {pt})$
with
$H^{*}_{T^{\prime }_{\mathbb {R}}}(\mathrm {pt})$
with
![]() $S_{T'}$
. Furthermore, using the framing
$S_{T'}$
. Furthermore, using the framing
![]() $f \in \mathbb {Z}$
, we take a weight restriction to define
$f \in \mathbb {Z}$
, we take a weight restriction to define
In this paper, we will only need to work with insertions for which the above weight restriction of the disk invariant is defined.
The completion of the semigroup ring of
![]() $E(X,L)$
is
$E(X,L)$
is

in which we introduce the new formal variable
![]() $\mathsf {X}_0$
for the last component. Note that the isomorphism
$\mathsf {X}_0$
for the last component. Note that the isomorphism
![]() $\iota _*:E(X,L) \cong E(\widetilde {X})$
induces an isomorphism
$\iota _*:E(X,L) \cong E(\widetilde {X})$
induces an isomorphism
![]() $\Lambda _{X,L} \cong \Lambda _{\widetilde {X}}$
under the change of variables
$\Lambda _{X,L} \cong \Lambda _{\widetilde {X}}$
under the change of variables
![]() $\widetilde {Q}^{\iota _*(\beta )} = Q^\beta $
,
$\widetilde {Q}^{\iota _*(\beta )} = Q^\beta $
,
![]() $\widetilde {Q}^{[l_{\iota (\tau _0)}]} = \mathsf {X}_0$
. We will also use the equivariant version
$\widetilde {Q}^{[l_{\iota (\tau _0)}]} = \mathsf {X}_0$
. We will also use the equivariant version
Consider the basis
![]() $\{\phi _1,\dots ,\phi _m\}$
of
$\{\phi _1,\dots ,\phi _m\}$
of
![]() $H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
and
$H^{*}_{T'}(X) \otimes _{R_{T'}} S_{T'}$
and
![]() $t = \sum _{i=1}^m t^i \phi _i$
as in Section 3.1. Let
$t = \sum _{i=1}^m t^i \phi _i$
as in Section 3.1. Let
![]() $t^o$
be an additional formal variable for the open sector. The
$t^o$
be an additional formal variable for the open sector. The
![]() $T_f$
-equivariant disk potential of
$T_f$
-equivariant disk potential of
![]() $(X,L,f)$
is the following generating functions of disk invariants:
$(X,L,f)$
is the following generating functions of disk invariants:

Conceptually, we may view
![]() $t^o$
as parameterizing a divisor-like insertion arising from the open sector and
$t^o$
as parameterizing a divisor-like insertion arising from the open sector and
![]() $\mathsf {X} := e^{t^o}\mathsf {X}_0$
as parameterizing the winding numbers of disk invariants. Note that
$\mathsf {X} := e^{t^o}\mathsf {X}_0$
as parameterizing the winding numbers of disk invariants. Note that
![]() $F_{0,1}^{X,(L, f)}$
is supported on the ideal of
$F_{0,1}^{X,(L, f)}$
is supported on the ideal of
![]() $\Lambda _{X,L}$
generated by
$\Lambda _{X,L}$
generated by
![]() $\mathsf {X}_0$
. For later use, we introduce the following modified version:
$\mathsf {X}_0$
. For later use, we introduce the following modified version:

where
![]() $\int $
is interpreted as taking the antiderivative with respect to
$\int $
is interpreted as taking the antiderivative with respect to
![]() $t^o$
. We note that the insertions
$t^o$
. We note that the insertions
![]() $\phi _1, \dots , \phi _m$
are homogeneous of degree 0 and do not introduce additional poles along
$\phi _1, \dots , \phi _m$
are homogeneous of degree 0 and do not introduce additional poles along
![]() $\mathsf {u}_2-f\mathsf {u}_1$
. Thus, the weight restriction to
$\mathsf {u}_2-f\mathsf {u}_1$
. Thus, the weight restriction to
![]() $\mathsf {u}_2 - f\mathsf {u}_1 = 0$
in the definition of the disks invariants in
$\mathsf {u}_2 - f\mathsf {u}_1 = 0$
in the definition of the disks invariants in
![]() $F_{0,1}^{X,(L, f)}$
is valid. Similarly, it is valid to apply this weight restriction to the closed invariants of X in
$F_{0,1}^{X,(L, f)}$
is valid. Similarly, it is valid to apply this weight restriction to the closed invariants of X in
![]() $F_0^{X,T'}$
.
$F_0^{X,T'}$
.
3.3 Open/closed correspondence
The open/closed correspondence [Reference Liu and Yu33, Reference Liu and Yu34] identifies the genus-zero open Gromov-Witten theory of
![]() $(X,L,f)$
and closed Gromov-Witten theory of
$(X,L,f)$
and closed Gromov-Witten theory of
![]() $\widetilde {X}$
at the numerical level of invariants as well as the level of generating functions. In this paper, we use the following statement of the correspondence. We introduce the notation
$\widetilde {X}$
at the numerical level of invariants as well as the level of generating functions. In this paper, we use the following statement of the correspondence. We introduce the notation
 $$ \begin{align} \mathsf{v} := \begin{cases} \widetilde{\mathbf{w}}(\widetilde{\tau}_2, \widetilde{\sigma}_0) = \mathsf{u}_2 - f\mathsf{u}_1 & \text{if } f \ge 0,\\ -\widetilde{\mathbf{w}}(\widetilde{\tau}_3, \widetilde{\sigma}_0) = \mathsf{u}_2 - f\mathsf{u}_1 + \mathsf{u}_4 & \text{if } f < 0. \end{cases} \end{align} $$
$$ \begin{align} \mathsf{v} := \begin{cases} \widetilde{\mathbf{w}}(\widetilde{\tau}_2, \widetilde{\sigma}_0) = \mathsf{u}_2 - f\mathsf{u}_1 & \text{if } f \ge 0,\\ -\widetilde{\mathbf{w}}(\widetilde{\tau}_3, \widetilde{\sigma}_0) = \mathsf{u}_2 - f\mathsf{u}_1 + \mathsf{u}_4 & \text{if } f < 0. \end{cases} \end{align} $$
Theorem 3.1 [Reference Liu and Yu34].
The Gromov-Witten potential
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
of
$F_0^{\widetilde {X},\widetilde {T}'}$
of
![]() $\widetilde {X}$
can be expanded as
$\widetilde {X}$
can be expanded as
 $$ \begin{align} \begin{aligned} F_0^{\widetilde{X},\widetilde{T}'}(t^1, \dots, t^m, t^{m+1}) = & \frac{(t^{m+1})^3}{6\Delta^{m+1,\widetilde{T}'}} + \mathsf{u}_4^{-1}\widetilde{A}(t^1, \dots, t^m) + \mathsf{v}^{-1}\widetilde{B}(t^1, \dots, t^m, t^{m+1}) \\ & + \mathsf{u}_4\mathsf{v}^{-1}\widetilde{C}_1 (t^1, \dots, t^m, t^{m+1}) + \widetilde{C}_2(t^1, \dots, t^m, t^{m+1}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} F_0^{\widetilde{X},\widetilde{T}'}(t^1, \dots, t^m, t^{m+1}) = & \frac{(t^{m+1})^3}{6\Delta^{m+1,\widetilde{T}'}} + \mathsf{u}_4^{-1}\widetilde{A}(t^1, \dots, t^m) + \mathsf{v}^{-1}\widetilde{B}(t^1, \dots, t^m, t^{m+1}) \\ & + \mathsf{u}_4\mathsf{v}^{-1}\widetilde{C}_1 (t^1, \dots, t^m, t^{m+1}) + \widetilde{C}_2(t^1, \dots, t^m, t^{m+1}), \end{aligned} \end{align} $$
where
-
(a) Each of
 $\widetilde {A}, \widetilde {B}, \widetilde {C}_1, \widetilde {C}_2$
has a well-defined weight restriction to
$\widetilde {A}, \widetilde {B}, \widetilde {C}_1, \widetilde {C}_2$
has a well-defined weight restriction to
 $\mathsf {u}_4 = 0, \mathsf {u}_2 - f\mathsf {u}_1 = 0$
.
$\mathsf {u}_4 = 0, \mathsf {u}_2 - f\mathsf {u}_1 = 0$
. -
(b)
 $\widetilde {A}$
is supported on the Novikov variables
$\widetilde {A}$
is supported on the Novikov variables
 $\{\widetilde {Q}^{\iota _*(\beta )}: \beta \in E(X)\}$
and after the change of variables
$\{\widetilde {Q}^{\iota _*(\beta )}: \beta \in E(X)\}$
and after the change of variables $$ \begin{align*}\widetilde{A}(t^1, \dots, t^m) \big|_{\mathsf{u}_4 = 0} = F_0^{X,T'}(t^1, \dots, t^m) \end{align*} $$
$$ \begin{align*}\widetilde{A}(t^1, \dots, t^m) \big|_{\mathsf{u}_4 = 0} = F_0^{X,T'}(t^1, \dots, t^m) \end{align*} $$
 $\widetilde {Q}^{\iota _*(\beta )} = Q^\beta $
.
$\widetilde {Q}^{\iota _*(\beta )} = Q^\beta $
.
-
(c) We have
after the change of variables $$ \begin{align*} \widetilde{B}(t^1, \dots, t^m, t^{m+1}) \big|_{\mathsf{u}_4 = 0, \mathsf{u}_2 - f\mathsf{u}_1 = 0} = \int F_{0,1}^{X,(L, f)}(t^1, \dots, t^m, t^o) \end{align*} $$
$$ \begin{align*} \widetilde{B}(t^1, \dots, t^m, t^{m+1}) \big|_{\mathsf{u}_4 = 0, \mathsf{u}_2 - f\mathsf{u}_1 = 0} = \int F_{0,1}^{X,(L, f)}(t^1, \dots, t^m, t^o) \end{align*} $$
 $\widetilde {Q}^{\iota _*(\beta )} = Q^\beta $
,
$\widetilde {Q}^{\iota _*(\beta )} = Q^\beta $
,
 $\widetilde {Q}^{[l_{\iota (\tau _0)}]} = \mathsf {X}_0$
, and
$\widetilde {Q}^{[l_{\iota (\tau _0)}]} = \mathsf {X}_0$
, and
 $t^{m+1} = -\mathsf {u}_1 t^o$
.
$t^{m+1} = -\mathsf {u}_1 t^o$
.
The statement of Theorem 3.1 differs from the results in [Reference Liu and Yu34], particularly Theorems 4.1 and 5.4 there, in that it uses the classes
![]() $\phi _1,\dots ,\phi _m$
and their counterparts
$\phi _1,\dots ,\phi _m$
and their counterparts
![]() $\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m$
to parameterize insertions, and that it also involves closed Gromov-Witten invariants of X. Nevertheless, it directly follows from the localization analysis and vanishing arguments in [Reference Liu and Yu34, Section 4]. We defer the derivation details to Appendix A.1.
$\widetilde {\phi }_1,\dots ,\widetilde {\phi }_m$
to parameterize insertions, and that it also involves closed Gromov-Witten invariants of X. Nevertheless, it directly follows from the localization analysis and vanishing arguments in [Reference Liu and Yu34, Section 4]. We defer the derivation details to Appendix A.1.
4 Frobenius structures on closed Gromov-Witten theory
In this section, we review the equivariant formal Frobenius structures determined by the closed Gromov-Witten theory of X,
![]() $\widetilde {X}$
and specifically the WDVV equations. Under the open/closed correspondence, we use the WDVV equation for
$\widetilde {X}$
and specifically the WDVV equations. Under the open/closed correspondence, we use the WDVV equation for
![]() $\widetilde {X}$
to deduce a collection of non-linear partial differential equations that involve the open and closed Gromov-Witten invariants of
$\widetilde {X}$
to deduce a collection of non-linear partial differential equations that involve the open and closed Gromov-Witten invariants of
![]() $(X,L)$
(Proposition 4.4).
$(X,L)$
(Proposition 4.4).
4.1 Formal Frobenius and F-manifolds
We first recall the definition of formal Frobenius manifolds over a general base ring R which is a commutative algebra over
![]() $ {\mathbb {C}} $
, extending Definition 1.2. We refer to [Reference Lee and Pandharipande30, Chapter 2] for additional details.
$ {\mathbb {C}} $
, extending Definition 1.2. We refer to [Reference Lee and Pandharipande30, Chapter 2] for additional details.
Definition 4.1. A formal Frobenius manifold over R consists of the data
![]() $(\hat {M},g,A,\mathbf {1})$
where
$(\hat {M},g,A,\mathbf {1})$
where
-
1.
 is a formal manifold over R defined by the completion of a free R-module K of rank m at the origin, where
is a formal manifold over R defined by the completion of a free R-module K of rank m at the origin, where
 $K^\vee := \mathrm {Hom}_R(K,R)$
;
$K^\vee := \mathrm {Hom}_R(K,R)$
; -
2. g is a formal, flat, R-linear, symmetric, nondegenerate quadratic form on the formal tangent bundle
 $\mathcal {T}_{\hat {M}}$
over R;
$\mathcal {T}_{\hat {M}}$
over R; -
3. A is a formal, R-linear, symmetric tensor
 $$ \begin{align*}A:\mathcal{T}_{\hat{M}}\otimes \mathcal{T}_{\hat{M}}\otimes \mathcal{T}_{\hat{M}} \to \mathcal{O}_{\hat{M}}. \end{align*} $$
$$ \begin{align*}A:\mathcal{T}_{\hat{M}}\otimes \mathcal{T}_{\hat{M}}\otimes \mathcal{T}_{\hat{M}} \to \mathcal{O}_{\hat{M}}. \end{align*} $$
-
4.
 $\mathbf {1}$
is a formal vector field on
$\mathbf {1}$
is a formal vector field on
 $\hat {M}$
over R.
$\hat {M}$
over R.
The above data are required to satisfy the potentiality, associativity, and unit conditions as in Definition 1.2.
A formal Frobenius manifold
![]() $\hat {M}$
over R may alternatively be viewed as a relative formal complex Frobenius manifold over the affine base
$\hat {M}$
over R may alternatively be viewed as a relative formal complex Frobenius manifold over the affine base
![]() $\mathrm {Spec} (R)$
. Elements in R pull back to constants in the structure sheaf
$\mathrm {Spec} (R)$
. Elements in R pull back to constants in the structure sheaf
![]() $\mathcal {O}_{\hat {M}}$
.
$\mathcal {O}_{\hat {M}}$
.
Given a formal Frobenius manifold ![]() as above, the origin is the only point in
as above, the origin is the only point in
![]() $\hat {M}$
and
$\hat {M}$
and
![]() $\mathcal {T}_{\hat {M}} \cong K \otimes _R \mathcal {O}_{\hat {M}}$
. The product
$\mathcal {T}_{\hat {M}} \cong K \otimes _R \mathcal {O}_{\hat {M}}$
. The product
![]() $\star $
defined by the associativity condition specializes to an R-algebra
$\star $
defined by the associativity condition specializes to an R-algebra
![]() $(K, \star )$
at the origin.
$(K, \star )$
at the origin.
Definition 4.2. A formal Frobenius manifold
![]() $\hat {M}$
over R is semi-simple if the induced R-algebra
$\hat {M}$
over R is semi-simple if the induced R-algebra ![]() is isomorphic to
is isomorphic to ![]() with the product algebra structure.
with the product algebra structure.
Similarly, we may define flat formal F-manifolds over the general base ring R, extending Definition 1.4.
Definition 4.3. A flat formal F-manifold over R consists of the data
![]() $(\hat {M},\nabla ,\star ,\mathbf {1})$
where
$(\hat {M},\nabla ,\star ,\mathbf {1})$
where
-
1.
 is a formal manifold over R defined by the completion of a free R-module K of rank
is a formal manifold over R defined by the completion of a free R-module K of rank
 $m+1$
at the origin;
$m+1$
at the origin; -
2.
 $\nabla $
is an R-linear connection on the formal tangent bundle
$\nabla $
is an R-linear connection on the formal tangent bundle
 $\mathcal {T}_{\hat {M}}$
,
$\mathcal {T}_{\hat {M}}$
, -
3.
 $\star $
defines an algebra structure on
$\star $
defines an algebra structure on
 $\mathcal {T}_{\hat {M}}$
,
$\mathcal {T}_{\hat {M}}$
, -
4.
 $\mathbf {1}$
is a
$\mathbf {1}$
is a
 $\nabla $
-flat formal vector field on
$\nabla $
-flat formal vector field on
 $\hat {M}$
over R which is a unit for
$\hat {M}$
over R which is a unit for
 $\star $
.
$\star $
.
The above data satisfy the condition that the connection
![]() $\nabla ^z:=\nabla -\frac {1}{z}\star $
is flat and symmetric for any
$\nabla ^z:=\nabla -\frac {1}{z}\star $
is flat and symmetric for any
![]() $z\in \mathbb {P}^1$
.
$z\in \mathbb {P}^1$
.
4.2 Gromov-Witten case
Let
![]() $\mathcal {X}$
be a smooth projective variety. Let
$\mathcal {X}$
be a smooth projective variety. Let
![]() $\{T_i\}_{i=1}^m$
be a basis of
$\{T_i\}_{i=1}^m$
be a basis of
![]() $H^{*}(\mathcal {X})$
and
$H^{*}(\mathcal {X})$
and
![]() $t^1,\dots ,t^m$
be the corresponding coordinates. Consider the genus-zero Gromov-Witten potential
$t^1,\dots ,t^m$
be the corresponding coordinates. Consider the genus-zero Gromov-Witten potential
![]() $F_0^{\mathcal {X}}$
of
$F_0^{\mathcal {X}}$
of
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
and
![]() $(g^{ij})=(g_{ij})^{-1}$
.
$(g^{ij})=(g_{ij})^{-1}$
.
Let
![]() $\partial _i := \frac {\partial }{\partial t^i}$
. As stated in Theorem 1.1, for any
$\partial _i := \frac {\partial }{\partial t^i}$
. As stated in Theorem 1.1, for any
![]() $i,j,k,l\in \{1,\dots ,m\}$
, the following WDVV equation holds:
$i,j,k,l\in \{1,\dots ,m\}$
, the following WDVV equation holds:
For any
![]() $i,j\in \{1,\dots ,m\}$
, we define the quantum product
$i,j\in \{1,\dots ,m\}$
, we define the quantum product
![]() $T_i\star _t T_j$
as
$T_i\star _t T_j$
as
 $$ \begin{align*}(T_i\star_t T_j,T_k)_{\mathcal{X}}=\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^k}. \end{align*} $$
$$ \begin{align*}(T_i\star_t T_j,T_k)_{\mathcal{X}}=\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^k}. \end{align*} $$
The WDVV equation implies that the quantum product
![]() $\star _t$
is associative.
$\star _t$
is associative.
Moreover, we can define a formal Frobenius manifold as follows. Let
where
![]() $\Lambda _{\mathcal {X}}$
is the Novikov ring of
$\Lambda _{\mathcal {X}}$
is the Novikov ring of
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
![]() $\hat {H}$
be the formal completion of H along the origin:
$\hat {H}$
be the formal completion of H along the origin:
Let
![]() $\mathcal {O}_{\hat {H}}$
be the structure sheaf on
$\mathcal {O}_{\hat {H}}$
be the structure sheaf on
![]() $\hat {H}$
and
$\hat {H}$
and
![]() $\mathcal {T}_{\hat {H}}$
be the tangent sheaf on
$\mathcal {T}_{\hat {H}}$
be the tangent sheaf on
![]() $\hat {H}$
. Then
$\hat {H}$
. Then
![]() $\mathcal {T}_{\hat {H}}$
is a sheaf of free
$\mathcal {T}_{\hat {H}}$
is a sheaf of free
![]() $\mathcal {O}_{\hat {H}}$
-modules of rank N. Given an open set U in
$\mathcal {O}_{\hat {H}}$
-modules of rank N. Given an open set U in
![]() $\hat {H}$
, we have
$\hat {H}$
, we have
 $$ \begin{align*}\mathcal{T}_{\hat{H}}(U) \cong \bigoplus_{i=1}^m \mathcal{O}_{\hat{H}}(U) \frac{\partial}{\partial t^{i}}. \end{align*} $$
$$ \begin{align*}\mathcal{T}_{\hat{H}}(U) \cong \bigoplus_{i=1}^m \mathcal{O}_{\hat{H}}(U) \frac{\partial}{\partial t^{i}}. \end{align*} $$
The quantum product and the Poincaré pairing define the structure of a formal Frobenius manifold on
![]() $\hat {H}$
over
$\hat {H}$
over
![]() $\Lambda _{\mathcal {X}}$
:
$\Lambda _{\mathcal {X}}$
:
 $$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t \frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)_{\mathcal{X}}=\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^k}, \qquad \left(\frac{\partial}{\partial t^i}, \frac{\partial}{\partial t^j}\right)_{\mathcal{X}}=g_{ij}. \end{align*} $$
$$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t \frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)_{\mathcal{X}}=\frac{\partial^3 F_0^{\mathcal{X}}}{\partial t^i\partial t^j\partial t^k}, \qquad \left(\frac{\partial}{\partial t^i}, \frac{\partial}{\partial t^j}\right)_{\mathcal{X}}=g_{ij}. \end{align*} $$
The generalization of the WDVV equation to the equivariant setting is straightforward. Suppose
![]() $\mathcal {X}$
admits an action of a torus
$\mathcal {X}$
admits an action of a torus
![]() $\mathbb {T}$
and let
$\mathbb {T}$
and let
![]() $\{T_i\}_{i=1}^m$
be a basis of
$\{T_i\}_{i=1}^m$
be a basis of
![]() $H^{*}_{\mathbb {T}}(\mathcal {X})$
. One only needs to replace
$H^{*}_{\mathbb {T}}(\mathcal {X})$
. One only needs to replace
![]() $F_0^{\mathcal {X}}$
by the genus-zero
$F_0^{\mathcal {X}}$
by the genus-zero
![]() $\mathbb {T}$
-equivariant Gromov-Witten potential
$\mathbb {T}$
-equivariant Gromov-Witten potential
![]() $F_0^{\mathcal {X},\mathbb {T}}$
and replace
$F_0^{\mathcal {X},\mathbb {T}}$
and replace
![]() $( T_i,T_j)_{\mathcal {X}}$
by the
$( T_i,T_j)_{\mathcal {X}}$
by the
![]() $\mathbb {T}$
-equivariant Poincaré pairing
$\mathbb {T}$
-equivariant Poincaré pairing
![]() $( T_i,T_j)_{\mathcal {X},\mathbb {T}}$
. Then the WDVV equation (Theorem 1.1) still holds. Moreover, in the equivariant setting,
$( T_i,T_j)_{\mathcal {X},\mathbb {T}}$
. Then the WDVV equation (Theorem 1.1) still holds. Moreover, in the equivariant setting,
![]() $\mathcal {X}$
can be allowed to be non-compact. We only need
$\mathcal {X}$
can be allowed to be non-compact. We only need
![]() $\overline {\mathcal {M}}_{g,n}(\mathcal {X},\beta )^{\mathbb {T}}$
to be compact in order to define
$\overline {\mathcal {M}}_{g,n}(\mathcal {X},\beta )^{\mathbb {T}}$
to be compact in order to define
![]() $\mathbb {T}$
-equivariant Gromov-Witten invariants of
$\mathbb {T}$
-equivariant Gromov-Witten invariants of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
In the equivariant setting, we can still define a formal Frobenius manifold as follows. Let
where
![]() $\Lambda _{\mathcal {X}}^{\mathbb {T}}$
is the base change of
$\Lambda _{\mathcal {X}}^{\mathbb {T}}$
is the base change of
![]() $\Lambda _{\mathcal {X}}$
to adjoin equivariant parameters of
$\Lambda _{\mathcal {X}}$
to adjoin equivariant parameters of
![]() $\mathbb {T}$
. Let
$\mathbb {T}$
. Let
![]() $\hat {H}$
be the formal completion of H along the origin:
$\hat {H}$
be the formal completion of H along the origin:
Let
![]() $\mathcal {O}_{\hat {H}}$
be the structure sheaf on
$\mathcal {O}_{\hat {H}}$
be the structure sheaf on
![]() $\hat {H}$
and
$\hat {H}$
and
![]() $\mathcal {T}_{\hat {H}}$
be the tangent sheaf on
$\mathcal {T}_{\hat {H}}$
be the tangent sheaf on
![]() $\hat {H}$
. Then
$\hat {H}$
. Then
![]() $\mathcal {T}_{\hat {H}}$
is a sheaf of free
$\mathcal {T}_{\hat {H}}$
is a sheaf of free
![]() $\mathcal {O}_{\hat {H}}$
-modules of rank m. Given an open set U in
$\mathcal {O}_{\hat {H}}$
-modules of rank m. Given an open set U in
![]() $\hat {H}$
, we have
$\hat {H}$
, we have
 $$ \begin{align*}\mathcal{T}_{\hat{H}}(U) \cong \bigoplus_{i=1}^m \mathcal{O}_{\hat{H}}(U) \frac{\partial}{\partial t^{i}}. \end{align*} $$
$$ \begin{align*}\mathcal{T}_{\hat{H}}(U) \cong \bigoplus_{i=1}^m \mathcal{O}_{\hat{H}}(U) \frac{\partial}{\partial t^{i}}. \end{align*} $$
The quantum product and the
![]() $\mathbb {T}$
-equivariant Poincaré pairing define the structure of a formal Frobenius manifold on
$\mathbb {T}$
-equivariant Poincaré pairing define the structure of a formal Frobenius manifold on
![]() $\hat {H}$
over
$\hat {H}$
over
![]() $\Lambda _{\mathcal {X}}^{\mathbb {T}}$
:
$\Lambda _{\mathcal {X}}^{\mathbb {T}}$
:
 $$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t \frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)_{\mathcal{X},\mathbb{T}}=\frac{\partial^3 F_0^{\mathcal{X},\mathbb{T}}}{\partial t^i\partial t^j\partial t^k}, \qquad \left(\frac{\partial}{\partial t^i}, \frac{\partial}{\partial t^j}\right)_{\mathcal{X},\mathbb{T}}=g_{ij}. \end{align*} $$
$$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t \frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)_{\mathcal{X},\mathbb{T}}=\frac{\partial^3 F_0^{\mathcal{X},\mathbb{T}}}{\partial t^i\partial t^j\partial t^k}, \qquad \left(\frac{\partial}{\partial t^i}, \frac{\partial}{\partial t^j}\right)_{\mathcal{X},\mathbb{T}}=g_{ij}. \end{align*} $$
4.3 Specializing to X and
 $\widetilde {X}$
$\widetilde {X}$
Now we specialize to the toric Calabi-Yau 3-fold X and the toric Calabi-Yau 4-fold
![]() $\widetilde {X}$
. Recall from Section 2.6 that we defined the bases
$\widetilde {X}$
. Recall from Section 2.6 that we defined the bases
![]() $\{\phi _1, \dots , \phi _m\}$
,
$\{\phi _1, \dots , \phi _m\}$
,
![]() $\{\widetilde {\phi }_1, \dots , \widetilde {\phi }_{m+1}\}$
of
$\{\widetilde {\phi }_1, \dots , \widetilde {\phi }_{m+1}\}$
of
![]() $H^{*}_{T'}(X)$
,
$H^{*}_{T'}(X)$
,
![]() $H^{*}_{\widetilde {T}'}(\widetilde {X})$
, respectively. Let
$H^{*}_{\widetilde {T}'}(\widetilde {X})$
, respectively. Let
be the induced equivariant formal Frobenius manifolds constructed as in Section 4.2. The quantum products are given by the closed Gromov-Witten potentials
![]() $F_0^{X,T'}, F_0^{\widetilde {X},\widetilde {T}'}$
, respectively. The equivariant Poincaré parings are diagonal:
$F_0^{X,T'}, F_0^{\widetilde {X},\widetilde {T}'}$
, respectively. The equivariant Poincaré parings are diagonal:
 $$ \begin{align*} &g_{ij} := (\phi_i,\phi_j)_{X,T'}=\frac{\delta_{ij}}{\Delta^{i,T'}}, && i,j \in \{1, \dots, m\};\\ &\widetilde{g}_{ij} := (\widetilde{\phi}_i,\widetilde{\phi}_j)_{\widetilde{X},\widetilde{T}'}=\frac{\delta_{ij}}{\Delta^{i,\widetilde{T}'}}, && i,j \in \{1, \dots, m+1\}. \end{align*} $$
$$ \begin{align*} &g_{ij} := (\phi_i,\phi_j)_{X,T'}=\frac{\delta_{ij}}{\Delta^{i,T'}}, && i,j \in \{1, \dots, m\};\\ &\widetilde{g}_{ij} := (\widetilde{\phi}_i,\widetilde{\phi}_j)_{\widetilde{X},\widetilde{T}'}=\frac{\delta_{ij}}{\Delta^{i,\widetilde{T}'}}, && i,j \in \{1, \dots, m+1\}. \end{align*} $$
Note that for
![]() $i = 1, \dots , m$
we have
$i = 1, \dots , m$
we have
Let
![]() $(g^{ij})=(g_{ij})^{-1}$
and
$(g^{ij})=(g_{ij})^{-1}$
and
![]() $(\widetilde {g}^{ij})=(\widetilde {g}_{ij})^{-1}$
. For any
$(\widetilde {g}^{ij})=(\widetilde {g}_{ij})^{-1}$
. For any
![]() $i,j,k,l \in \{1, \dots , m\}$
, the WDVV equation for X reads
$i,j,k,l \in \{1, \dots , m\}$
, the WDVV equation for X reads
where the summation index
![]() $\nu $
runs through
$\nu $
runs through
![]() $1, \dots , m$
. For any
$1, \dots , m$
. For any
![]() $i,j,k,l \in \{1, \dots , m+1\}$
, the WDVV equation for
$i,j,k,l \in \{1, \dots , m+1\}$
, the WDVV equation for
![]() $\widetilde {X}$
reads
$\widetilde {X}$
reads
where the summation index
![]() $\nu $
runs through
$\nu $
runs through
![]() $1, \dots , m+1$
.
$1, \dots , m+1$
.
4.4 Recursive relations for open and closed invariants
Now we combine the WDVV equation (11) for
![]() $\widetilde {X}$
and the open/closed correspondence (Theorem 3.1) to obtain the following non-linear partial differential equations for the closed Gromov-Witten potential
$\widetilde {X}$
and the open/closed correspondence (Theorem 3.1) to obtain the following non-linear partial differential equations for the closed Gromov-Witten potential
![]() $F_0^{X,T'}$
of X and the disk potential
$F_0^{X,T'}$
of X and the disk potential
![]() $F_{0,1}^{X,(L, f)}$
of
$F_{0,1}^{X,(L, f)}$
of
![]() $(X, L, f)$
. For
$(X, L, f)$
. For
![]() $i,j \in \{1, \dots , m\}$
, we set
$i,j \in \{1, \dots , m\}$
, we set
which is well-defined by Assumption 2.2. Let
![]() $(h^{ij})=(h_{ij})^{-1}$
.
$(h^{ij})=(h_{ij})^{-1}$
.
Proposition 4.4. Denote
![]() $\partial _o := \frac {\partial }{\partial t^o}$
. We have
$\partial _o := \frac {\partial }{\partial t^o}$
. We have
-
(I) For
 $i, j, k, l \in \{1, \dots , m\}$
:
$i, j, k, l \in \{1, \dots , m\}$
:-
(Ia)
 $$ \begin{align*} &\hskip-1pc \partial_i\partial_j\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l \int\kern-1pt F_{0,1}^{X,(L, f)} + \partial_i\partial_j\partial_\nu \int\kern-1pt F_{0,1}^{X,(L, f)} \cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\\ &\quad = \partial_j\partial_k\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l \int F_{0,1}^{X,(L, f)}\\ &\qquad + \partial_j\partial_k\partial_\nu \int F_{0,1}^{X,(L, f)} \cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}; \end{align*} $$
$$ \begin{align*} &\hskip-1pc \partial_i\partial_j\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l \int\kern-1pt F_{0,1}^{X,(L, f)} + \partial_i\partial_j\partial_\nu \int\kern-1pt F_{0,1}^{X,(L, f)} \cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\\ &\quad = \partial_j\partial_k\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l \int F_{0,1}^{X,(L, f)}\\ &\qquad + \partial_j\partial_k\partial_\nu \int F_{0,1}^{X,(L, f)} \cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}; \end{align*} $$
-
(Ib)
 $$ \begin{align*}\partial_i\partial_j\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l \int F_{0,1}^{X,(L, f)} =\partial_j\partial_k\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l \int F_{0,1}^{X,(L, f)}; \end{align*} $$
$$ \begin{align*}\partial_i\partial_j\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l \int F_{0,1}^{X,(L, f)} =\partial_j\partial_k\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l \int F_{0,1}^{X,(L, f)}; \end{align*} $$
-
(Ic)
 $$ \begin{align*}\partial_i\partial_j\partial_\nu F_0^{X,T'}\cdot g^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l F_0^{X,T'} =\partial_j\partial_k\partial_\nu F_0^{X,T'}\cdot g^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l F_0^{X,T'}. \end{align*} $$
$$ \begin{align*}\partial_i\partial_j\partial_\nu F_0^{X,T'}\cdot g^{\nu\nu}\cdot \partial_\nu\partial_k\partial_l F_0^{X,T'} =\partial_j\partial_k\partial_\nu F_0^{X,T'}\cdot g^{\nu\nu}\cdot \partial_\nu\partial_i\partial_l F_0^{X,T'}. \end{align*} $$
-
-
(II) For
 $i, j, k \in \{1, \dots , m\}$
:
$i, j, k \in \{1, \dots , m\}$
:-
(IIa)
 $$ \begin{align*}\partial_i\partial_j\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu} & \cdot \partial_\nu\partial_k\partial_o \int F_{0,1}^{X,(L, f)} =\partial_j\partial_k\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0} \\ &\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_o \int F_{0,1}^{X,(L, f)}; \end{align*} $$
$$ \begin{align*}\partial_i\partial_j\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu} & \cdot \partial_\nu\partial_k\partial_o \int F_{0,1}^{X,(L, f)} =\partial_j\partial_k\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0} \\ &\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_o \int F_{0,1}^{X,(L, f)}; \end{align*} $$
-
(IIb)
 $$ \begin{align*}\!\!\!\partial_i\partial_j\partial_\nu \kern-0.1pt\int\kern-0.1pt F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_o \kern-0.1pt\int F_{0,1}^{X,(L, f)} =\partial_j\partial_k\partial_\nu \kern-0.1pt\int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_o \kern-0.1pt\int\kern-0.1pt F_{0,1}^{X,(L, f)}. \end{align*} $$
$$ \begin{align*}\!\!\!\partial_i\partial_j\partial_\nu \kern-0.1pt\int\kern-0.1pt F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_k\partial_o \kern-0.1pt\int F_{0,1}^{X,(L, f)} =\partial_j\partial_k\partial_\nu \kern-0.1pt\int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_o \kern-0.1pt\int\kern-0.1pt F_{0,1}^{X,(L, f)}. \end{align*} $$
-
-
(III) For
 $i, j \in \{1, \dots , m\}$
:
$i, j \in \{1, \dots , m\}$
:-
(IIIa)
 $$ \begin{align*}\partial_i\partial_j\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_o\partial_o \int F_{0,1}^{X,(L, f)} -\mathsf{u}_1 \partial_i\partial_j\partial_o \int F_{0,1}^{X,(L, f)} =0; \end{align*} $$
$$ \begin{align*}\partial_i\partial_j\partial_\nu F_0^{X,T'}\big|_{\mathsf{u}_2 - f\mathsf{u}_1 = 0}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_o\partial_o \int F_{0,1}^{X,(L, f)} -\mathsf{u}_1 \partial_i\partial_j\partial_o \int F_{0,1}^{X,(L, f)} =0; \end{align*} $$
-
(IIIb)
 $$ \begin{align*} & \partial_i\partial_j\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_o\partial_o \int F_{0,1}^{X,(L, f)} \\ & \quad =\partial_j\partial_o\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_o \int F_{0,1}^{X,(L, f)}. \end{align*} $$
$$ \begin{align*} & \partial_i\partial_j\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_o\partial_o \int F_{0,1}^{X,(L, f)} \\ & \quad =\partial_j\partial_o\partial_\nu \int F_{0,1}^{X,(L, f)}\cdot h^{\nu\nu}\cdot \partial_\nu\partial_i\partial_o \int F_{0,1}^{X,(L, f)}. \end{align*} $$
-
Here, the summation index
![]() $\nu $
runs through
$\nu $
runs through
![]() $1, \dots , m$
. Identity (Ic) is valued in
$1, \dots , m$
. Identity (Ic) is valued in ![]() , while all the other identities are valued in
, while all the other identities are valued in ![]() .
.
In particular, (Ic) recovers the WDVV equation (10) for X.
Proof. The proposition directly follows from applying the expansion (9) in Theorem 3.1 to both sides of (11) and reading off appropriate coefficients, under the following rules:
-
• For (I), apply with
 $i,j,k,l$
as they are.
$i,j,k,l$
as they are. -
• For (II), apply with
 $i,j,k$
as they are and
$i,j,k$
as they are and
 $l = m+1$
.
$l = m+1$
. -
• For (III), apply with
 $i,j$
as they are and
$i,j$
as they are and
 $k = l = m+1$
.
$k = l = m+1$
. -
• For (Ia), (IIa), (IIIa), read off the coefficients of
 $\mathsf {v}^{-1}$
on both sides.
$\mathsf {v}^{-1}$
on both sides. -
• For (Ib), (IIb), (IIIb), read off the coefficients of
 $\mathsf {u}_4\mathsf {v}^{-2}$
on both sides.
$\mathsf {u}_4\mathsf {v}^{-2}$
on both sides. -
• For (Ic), read off the coefficients of
 $\mathsf {u}_4^{-1}$
on both sides.
$\mathsf {u}_4^{-1}$
on both sides.
Here, we use the following observation: We have
where the sign ‘
![]() $\pm $
’ is ‘
$\pm $
’ is ‘
![]() $+$
’ when
$+$
’ when
![]() $f \ge 0$
and ‘
$f \ge 0$
and ‘
![]() $-$
’ when
$-$
’ when
![]() $f<0$
(see (8) for the notation
$f<0$
(see (8) for the notation
![]() $\mathsf {v}$
). It has second-order zeroes along
$\mathsf {v}$
). It has second-order zeroes along
![]() $\mathsf {v}, \mathsf {u}_4$
, and thus, the
$\mathsf {v}, \mathsf {u}_4$
, and thus, the
![]() $\nu = m+1$
terms in (11) do not contribute to the result except for case (IIIa), where the triple derivative
$\nu = m+1$
terms in (11) do not contribute to the result except for case (IIIa), where the triple derivative
![]() $\partial _{m+1}\partial _{m+1}\partial _{m+1}\frac {(t^{m+1})^3}{6\Delta ^{m+1,\widetilde {T}'}}$
provides a cancelling factor
$\partial _{m+1}\partial _{m+1}\partial _{m+1}\frac {(t^{m+1})^3}{6\Delta ^{m+1,\widetilde {T}'}}$
provides a cancelling factor
![]() $\frac {1}{\Delta ^{m+1,\widetilde {T}'}}$
. Moreover, we change from
$\frac {1}{\Delta ^{m+1,\widetilde {T}'}}$
. Moreover, we change from
![]() $\partial _{m+1}$
to
$\partial _{m+1}$
to
![]() $\partial _o$
using the relation
$\partial _o$
using the relation
![]() $\partial _{m+1} = -\frac {\partial _o}{\mathsf {u}_1}$
.
$\partial _{m+1} = -\frac {\partial _o}{\mathsf {u}_1}$
.
Remark 4.5. Note that identities (IIa), (IIIa) of Proposition 4.4 resemble but are different from the open WDVV equation of [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] (stated in Theorem 1.3) for the disk potential with point-like boundary insertions, and the difference arises from how the
![]() $\nu = m+1$
terms contribute, as indicated in the proof above.
$\nu = m+1$
terms contribute, as indicated in the proof above.
5 Frobenius structures on open Gromov-Witten theory
In this section, we use the equations in Proposition 4.4 to construct Frobenius structures on the open and closed Gromov-Witten theory of
![]() $(X,L)$
, specifically,
$(X,L)$
, specifically,
-
• (Section 5.1, Theorems 5.5, 5.6) a semi-simple formal Frobenius manifold structure on
 where
where
 $\epsilon $
is a nilpotent variable with
$\epsilon $
is a nilpotent variable with
 $\epsilon ^2 = 0$
;
$\epsilon ^2 = 0$
; -
• (Section 5.2, Theorem 5.11) a flat formal F-manifold structure without unit on
 in which the
in which the
 $t^o$
-direction is nilpotent.
$t^o$
-direction is nilpotent.
Both structures can be viewed as extensions of the semi-simple formal Frobenius manifold
which is obtained from
![]() $\hat {H}_X$
by base change to
$\hat {H}_X$
by base change to
![]() $\Lambda _{X,L}^{T_f}$
.
$\Lambda _{X,L}^{T_f}$
.
5.1 A formal Frobenius structure
In this section, we construct a Frobenius structure on the formal scheme
over the base ring
Let
![]() $\mathcal {O}_{\hat {H}_1}$
be the structure sheaf on
$\mathcal {O}_{\hat {H}_1}$
be the structure sheaf on
![]() $\hat {H}_1$
and
$\hat {H}_1$
and
![]() $\mathcal {T}_{\hat {H}_1}$
be the tangent sheaf on
$\mathcal {T}_{\hat {H}_1}$
be the tangent sheaf on
![]() $\hat {H}_1$
. Then
$\hat {H}_1$
. Then
![]() $\mathcal {T}_{\hat {H}_1}$
is a sheaf of free
$\mathcal {T}_{\hat {H}_1}$
is a sheaf of free
![]() $\mathcal {O}_{\hat {H}_1}$
-modules of rank
$\mathcal {O}_{\hat {H}_1}$
-modules of rank
![]() $m+1$
. Given an open set U in
$m+1$
. Given an open set U in
![]() $\hat {H}_1$
, we have
$\hat {H}_1$
, we have
 $$ \begin{align*}\mathcal{T}_{\hat{H}_1}(U) \cong \bigoplus_{i=1}^m\mathcal{O}_{\hat{H}_1}(U) \frac{\partial}{\partial t^{i}}\bigoplus\mathcal{O}_{\hat{H}_1}(U)\frac{\partial}{\partial t^o}. \end{align*} $$
$$ \begin{align*}\mathcal{T}_{\hat{H}_1}(U) \cong \bigoplus_{i=1}^m\mathcal{O}_{\hat{H}_1}(U) \frac{\partial}{\partial t^{i}}\bigoplus\mathcal{O}_{\hat{H}_1}(U)\frac{\partial}{\partial t^o}. \end{align*} $$
We will construct a potential function F involving both the open and closed Gromov-Witten invariants of
![]() $(X, L)$
, as well as a pairing
$(X, L)$
, as well as a pairing
![]() $(-,-)$
on
$(-,-)$
on
![]() $\mathcal {T}_{\hat {H}_1}$
. We prove the associativity of the induced product
$\mathcal {T}_{\hat {H}_1}$
. We prove the associativity of the induced product
![]() $\star _t$
on
$\star _t$
on
![]() $\mathcal {T}_{\hat {H}_1}$
, which packages identities (Ia), (Ic), (IIa) and (IIIa) of Proposition 4.4. We show that the resulting tuple
$\mathcal {T}_{\hat {H}_1}$
, which packages identities (Ia), (Ic), (IIa) and (IIIa) of Proposition 4.4. We show that the resulting tuple
![]() $(\hat {H}_1,\star _t,(-,-))$
is a semi-simple formal Frobenius manifold.
$(\hat {H}_1,\star _t,(-,-))$
is a semi-simple formal Frobenius manifold.
5.1.1 Potential
Introduce the variable
![]() $\epsilon $
with
$\epsilon $
with
![]() $\epsilon ^2=0$
.
$\epsilon ^2=0$
.
Definition 5.1. We define the potential function F as
5.1.2 Pairing
In (12), we defined the restriction
![]() $(h_{ij})$
of the
$(h_{ij})$
of the
![]() $T'$
-equivariant Poincaré pairing
$T'$
-equivariant Poincaré pairing
![]() $(g_{ij})$
to
$(g_{ij})$
to
![]() $T_f$
. We now extend this pairing to the
$T_f$
. We now extend this pairing to the
![]() $t^o$
-direction. Recall that we have the change of variables
$t^o$
-direction. Recall that we have the change of variables
![]() $t^{m+1}=-\mathsf {u}_1 t^o$
from Theorem 3.1, which identifies
$t^{m+1}=-\mathsf {u}_1 t^o$
from Theorem 3.1, which identifies
![]() $\frac {\partial }{\partial t^o}$
with
$\frac {\partial }{\partial t^o}$
with
![]() $-\mathsf {u}_1\frac {\partial }{\partial t^{m+1}}$
. Moreover, we have
$-\mathsf {u}_1\frac {\partial }{\partial t^{m+1}}$
. Moreover, we have
 $$ \begin{align*}\left(\frac{\partial}{\partial t^{m+1}}, \frac{\partial}{\partial t^{m+1}}\right)_{\widetilde{X},\widetilde{T}'} = \widetilde{g}_{(m+1)(m+1)} =\frac{1}{(\mathsf{v}^2 \pm \mathsf{u}_4\mathsf{v}) \mathsf{u}_1(\mathsf{u}_1+\mathsf{u}_4)} \end{align*} $$
$$ \begin{align*}\left(\frac{\partial}{\partial t^{m+1}}, \frac{\partial}{\partial t^{m+1}}\right)_{\widetilde{X},\widetilde{T}'} = \widetilde{g}_{(m+1)(m+1)} =\frac{1}{(\mathsf{v}^2 \pm \mathsf{u}_4\mathsf{v}) \mathsf{u}_1(\mathsf{u}_1+\mathsf{u}_4)} \end{align*} $$
(see (13)). Clearing the second-order poles along
![]() $\mathsf {v}, \mathsf {u}_4$
, we set
$\mathsf {v}, \mathsf {u}_4$
, we set
Definition 5.2. We define the pairing
![]() $(-,-)$
on
$(-,-)$
on
![]() $\mathcal {T}_{\hat {H}_1}$
by the following: For any
$\mathcal {T}_{\hat {H}_1}$
by the following: For any
![]() $i,j\in \{1,\dots ,m,o\}$
,
$i,j\in \{1,\dots ,m,o\}$
,
 $$ \begin{align*}\left(\frac{\partial}{\partial t^i},\frac{\partial}{\partial t^j}\right) := h_{ij}. \end{align*} $$
$$ \begin{align*}\left(\frac{\partial}{\partial t^i},\frac{\partial}{\partial t^j}\right) := h_{ij}. \end{align*} $$
As before, let
![]() $(h^{ij})=(h_{ij})^{-1}$
.
$(h^{ij})=(h_{ij})^{-1}$
.
5.1.3 WDVV equations
Proposition 5.3. For any
![]() $i,j,k,l\in \{1,\dots ,m,o\}$
, the following WDVV equation holds:
$i,j,k,l\in \{1,\dots ,m,o\}$
, the following WDVV equation holds:
where the summation indices
![]() $\nu , \mu $
run through
$\nu , \mu $
run through
![]() $1, \dots , m, o$
.
$1, \dots , m, o$
.
Proof. Note that
![]() $(h^{ij})$
is diagonal and the summation is over
$(h^{ij})$
is diagonal and the summation is over
![]() $\nu = \mu $
. The proposition directly follows from identities (Ia), (Ic), (IIa) and (IIIa) of Proposition 4.4, under the following rules:
$\nu = \mu $
. The proposition directly follows from identities (Ia), (Ic), (IIa) and (IIIa) of Proposition 4.4, under the following rules:
-
• When
 $i,j,k,l \in \{1, \dots , m\}$
, the
$i,j,k,l \in \{1, \dots , m\}$
, the
 $\epsilon ^0$
-term of (16) follows from identity (Ic) and the
$\epsilon ^0$
-term of (16) follows from identity (Ic) and the
 $\epsilon ^1$
-term follows from (Ia).
$\epsilon ^1$
-term follows from (Ia). -
• When
 $i,j,k \in \{1, \dots , m\}$
,
$i,j,k \in \{1, \dots , m\}$
,
 $l = o$
, there is no
$l = o$
, there is no
 $\epsilon ^0$
-term in (16) and the
$\epsilon ^0$
-term in (16) and the
 $\epsilon ^1$
-term follows from (IIa).
$\epsilon ^1$
-term follows from (IIa). -
• When
 $i,j \in \{1, \dots , m\}$
,
$i,j \in \{1, \dots , m\}$
,
 $k = l = o$
, again there is no
$k = l = o$
, again there is no
 $\epsilon ^0$
-term in (16) and the
$\epsilon ^0$
-term in (16) and the
 $\epsilon ^1$
-term follows from (IIIa).
$\epsilon ^1$
-term follows from (IIIa).
Any other case is either trivial or symmetric to a case above. Here, we note that since
![]() $\epsilon ^2 = 0$
, the equation (16) does not contain terms involving a product of two copies of
$\epsilon ^2 = 0$
, the equation (16) does not contain terms involving a product of two copies of
![]() $F_{0,1}^{X,(L,f)}$
(or their antiderivatives).
$F_{0,1}^{X,(L,f)}$
(or their antiderivatives).
5.1.4 The formal Frobenius manifold
Definition 5.4. For any
![]() $i,j\in \{1,\dots ,m, o\}$
, define the product
$i,j\in \{1,\dots ,m, o\}$
, define the product
![]() $\frac {\partial }{\partial t^i}\star _t\frac {\partial }{\partial t^j}$
on
$\frac {\partial }{\partial t^i}\star _t\frac {\partial }{\partial t^j}$
on
![]() $\mathcal {T}_{\hat {H}_1}$
by
$\mathcal {T}_{\hat {H}_1}$
by
 $$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t\frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)=\frac{\partial^3F}{\partial t^i\partial t^j\partial t^k}, \end{align*} $$
$$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t\frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)=\frac{\partial^3F}{\partial t^i\partial t^j\partial t^k}, \end{align*} $$
where k ranges through
![]() $1,\dots ,m, o$
.
$1,\dots ,m, o$
.
By Proposition 5.3, the product
![]() $\star _t$
is indeed associative. Moreover, it is clear by definition that we have the compatibility condition
$\star _t$
is indeed associative. Moreover, it is clear by definition that we have the compatibility condition
 $$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t\frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)=\left(\frac{\partial}{\partial t^i},\frac{\partial}{\partial t^j}\star_t\frac{\partial}{\partial t^k}\right). \end{align*} $$
$$ \begin{align*}\left(\frac{\partial}{\partial t^i}\star_t\frac{\partial}{\partial t^j},\frac{\partial}{\partial t^k}\right)=\left(\frac{\partial}{\partial t^i},\frac{\partial}{\partial t^j}\star_t\frac{\partial}{\partial t^k}\right). \end{align*} $$
In other words, we have the following result.
Theorem 5.5. The tuple
![]() $(\hat {H}_1,\star _t,(-,-))$
is a formal Frobenius manifold over
$(\hat {H}_1,\star _t,(-,-))$
is a formal Frobenius manifold over
![]() $\Lambda _{X,L}^{T_f}[\epsilon ]$
.
$\Lambda _{X,L}^{T_f}[\epsilon ]$
.
5.1.5 Semi-simplicity of
 $\hat {H}_1$
$\hat {H}_1$
Let
![]() $S=\mathcal {O}_{\hat {H}_1}(\hat {H}_1)$
. Consider the global Frobenius algebra
$S=\mathcal {O}_{\hat {H}_1}(\hat {H}_1)$
. Consider the global Frobenius algebra
![]() $A=(\mathcal {T}_{\hat {H}_1}(\hat {H}_1),\star _t,(,))$
and let
$A=(\mathcal {T}_{\hat {H}_1}(\hat {H}_1),\star _t,(,))$
and let
![]() $I\subset S$
be the ideal generated by Q and
$I\subset S$
be the ideal generated by Q and
![]() $\mathsf {X}_0$
. Then A is a free S-module of rank
$\mathsf {X}_0$
. Then A is a free S-module of rank
![]() $m+1$
. Let
$m+1$
. Let
Then
![]() $A_n$
is a free
$A_n$
is a free
![]() $S_n$
-module of rank
$S_n$
-module of rank
![]() $m+1$
, and the ring structure
$m+1$
, and the ring structure
![]() $\star _t$
on A induces a ring structure
$\star _t$
on A induces a ring structure
![]() $*_{\underline {n}}$
on
$*_{\underline {n}}$
on
![]() $A_n$
. Note that
$A_n$
. Note that
![]() $A_1$
encodes the classical product. From the construction, the semi-simplicity of the (classical) Frobenius algebra (5) associated to
$A_1$
encodes the classical product. From the construction, the semi-simplicity of the (classical) Frobenius algebra (5) associated to
![]() $\widetilde {X}$
implies that
$\widetilde {X}$
implies that
![]() $A_1$
is semi-simple and
$A_1$
is semi-simple and
![]() $\{\xi _1^{(1)}:=\frac {\partial }{\partial t^1},\dots ,\xi _{m}^{(1)}:=\frac {\partial }{\partial t^{m}},\xi _o^{(1)}:=\frac {\partial }{\partial t^o}\}$
is a system of idempotent basis of
$\{\xi _1^{(1)}:=\frac {\partial }{\partial t^1},\dots ,\xi _{m}^{(1)}:=\frac {\partial }{\partial t^{m}},\xi _o^{(1)}:=\frac {\partial }{\partial t^o}\}$
is a system of idempotent basis of
![]() $A_1$
. For
$A_1$
. For
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\{ \xi _{i}^{(n+1)}:i=1,\dots ,m, o\}$
be the unique idempotent basis of
$\{ \xi _{i}^{(n+1)}:i=1,\dots ,m, o\}$
be the unique idempotent basis of
![]() $(A_{n+1},\star _{\underline {n+1}})$
which is the lift of the idempotent basis
$(A_{n+1},\star _{\underline {n+1}})$
which is the lift of the idempotent basis
![]() $\{ \xi _{i}^{(n)}:i=1,\dots ,m, o\}$
of
$\{ \xi _{i}^{(n)}:i=1,\dots ,m, o\}$
of
![]() $(A_n,\star _{\underline {n}})$
[Reference Lee and Pandharipande30, Lemma 16]. Then
$(A_n,\star _{\underline {n}})$
[Reference Lee and Pandharipande30, Lemma 16]. Then
is an idempotent basis of
![]() $(A,\star _t)$
. Therefore, we have the following result.
$(A,\star _t)$
. Therefore, we have the following result.
Theorem 5.6. The formal Frobenius manifold
![]() $(\hat {H}_1,\star _t,(-,-))$
is semi-simple.
$(\hat {H}_1,\star _t,(-,-))$
is semi-simple.
Remark 5.7. As discussed in Remark 1.7, the structural morphism
may be viewed as a submersion of (formal) supermanifolds over
![]() $\Lambda _{X,L}^{T_f}$
with
$\Lambda _{X,L}^{T_f}$
with
![]() $\epsilon $
viewed as an odd variable. Taking
$\epsilon $
viewed as an odd variable. Taking
![]() $\epsilon = 0$
, we obtain a Frobenius structure on the underlying reduced formal manifold, which we denote by
$\epsilon = 0$
, we obtain a Frobenius structure on the underlying reduced formal manifold, which we denote by
![]() $\hat {H}_{1, \mathrm {red}}$
. The induced global Frobenius algebra of
$\hat {H}_{1, \mathrm {red}}$
. The induced global Frobenius algebra of
![]() $\hat {H}_{1, \mathrm {red}}$
decomposes as the direct sum of the global Frobenius algebra of
$\hat {H}_{1, \mathrm {red}}$
decomposes as the direct sum of the global Frobenius algebra of
![]() $\hat {H}_X^f$
(defined in (14)) and a 1-dimensional Frobenius algebra over
$\hat {H}_X^f$
(defined in (14)) and a 1-dimensional Frobenius algebra over
![]() $\Lambda _{X,L}^{T_f}$
generated by
$\Lambda _{X,L}^{T_f}$
generated by
![]() $\frac {\partial }{\partial t^o}$
, and the decomposition is consistent with the semi-simplicity description above. In particular,
$\frac {\partial }{\partial t^o}$
, and the decomposition is consistent with the semi-simplicity description above. In particular,
![]() $\hat {H}_{1, \mathrm {red}}$
is semi-simple over
$\hat {H}_{1, \mathrm {red}}$
is semi-simple over
![]() $\Lambda _{X,L}^{T_f}$
, and
$\Lambda _{X,L}^{T_f}$
, and
![]() $\hat {H}_1$
may be viewed as an infinitesimal deformation of
$\hat {H}_1$
may be viewed as an infinitesimal deformation of
![]() $\hat {H}_{1, \mathrm {red}}$
.
$\hat {H}_{1, \mathrm {red}}$
.
5.2 A flat formal F-manifold structure
In this section, we construct a flat F-manifold structure on the formal scheme
over the base ring
![]() $\Lambda _{X,L}^{T_f}$
, where as compared to
$\Lambda _{X,L}^{T_f}$
, where as compared to
![]() $\hat {H}_1$
introduced in Section 5.1, we drop the variable
$\hat {H}_1$
introduced in Section 5.1, we drop the variable
![]() $\epsilon $
. Let
$\epsilon $
. Let
![]() $\mathcal {O}_{\hat {H}_2}$
be the structure sheaf on
$\mathcal {O}_{\hat {H}_2}$
be the structure sheaf on
![]() $\hat {H}_2$
and
$\hat {H}_2$
and
![]() $\mathcal {T}_{\hat {H}_2}$
be the tangent sheaf on
$\mathcal {T}_{\hat {H}_2}$
be the tangent sheaf on
![]() $\hat {H}_2$
. Then
$\hat {H}_2$
. Then
![]() $\mathcal {T}_{\hat {H}_2}$
is a sheaf of free
$\mathcal {T}_{\hat {H}_2}$
is a sheaf of free
![]() $\mathcal {O}_{\hat {H}_2}$
-modules of rank
$\mathcal {O}_{\hat {H}_2}$
-modules of rank
![]() $m+1$
. Given an open set U in
$m+1$
. Given an open set U in
![]() $\hat {H}_2$
, we have
$\hat {H}_2$
, we have
 $$ \begin{align*}\mathcal{T}_{\hat{H}_2}(U) \cong \bigoplus_{i=1}^m\mathcal{O}_{\hat{H}_2}(U) \frac{\partial}{\partial t^{i}}\bigoplus\mathcal{O}_{\hat{H}_2}(U)\frac{\partial}{\partial t^o}. \end{align*} $$
$$ \begin{align*}\mathcal{T}_{\hat{H}_2}(U) \cong \bigoplus_{i=1}^m\mathcal{O}_{\hat{H}_2}(U) \frac{\partial}{\partial t^{i}}\bigoplus\mathcal{O}_{\hat{H}_2}(U)\frac{\partial}{\partial t^o}. \end{align*} $$
We will construct a vector potential
![]() $\overline {F} = (F^1, \dots , F^m, F^o)$
whose second derivatives give structural coefficients for a product
$\overline {F} = (F^1, \dots , F^m, F^o)$
whose second derivatives give structural coefficients for a product
![]() $\star _t$
on
$\star _t$
on
![]() $\mathcal {T}_{\hat {H}_1}$
. We prove the associativity of
$\mathcal {T}_{\hat {H}_1}$
. We prove the associativity of
![]() $\star _t$
, which packages identities (Ia), (Ib), (Ic), (IIa) and (IIb) of Proposition 4.4.
$\star _t$
, which packages identities (Ia), (Ib), (Ic), (IIa) and (IIb) of Proposition 4.4.
5.2.1 Vector potential
Let
![]() $(h^{ij})$
be as defined in (12).
$(h^{ij})$
be as defined in (12).
Definition 5.8. We define the vector potential
![]() $\overline {F} = (F^1, \dots , F^m, F^o)$
by
$\overline {F} = (F^1, \dots , F^m, F^o)$
by
 $$ \begin{align*}F^i(t^1, \dots, t^m, t^o) := h^{ii} \partial_i \left(F_0^{X,T'}(t^1, \dots, t^m)\big|_{\mathsf{u}_2-f\mathsf{u}_1=0}+\int F_{0,1}^{X,(L,f)}(t^1, \dots, t^m,t^o=0)\right) \end{align*} $$
$$ \begin{align*}F^i(t^1, \dots, t^m, t^o) := h^{ii} \partial_i \left(F_0^{X,T'}(t^1, \dots, t^m)\big|_{\mathsf{u}_2-f\mathsf{u}_1=0}+\int F_{0,1}^{X,(L,f)}(t^1, \dots, t^m,t^o=0)\right) \end{align*} $$
for
![]() $i = 1, \dots , m$
and
$i = 1, \dots , m$
and
All components of
![]() $\overline {F}$
are functions that are independent of the variable
$\overline {F}$
are functions that are independent of the variable
![]() $t^o$
. As discussed in Remark 1.10, as we set
$t^o$
. As discussed in Remark 1.10, as we set
![]() $t^o = 0$
in the definitions, conceptually
$t^o = 0$
in the definitions, conceptually
![]() $\overline {F}$
has no insertions from the open sector. The
$\overline {F}$
has no insertions from the open sector. The
![]() $t^o$
-direction may also be viewed as an auxiliary direction in addition to the original m directions; see Remark 5.12.
$t^o$
-direction may also be viewed as an auxiliary direction in addition to the original m directions; see Remark 5.12.
5.2.2 Open WDVV equations
Proposition 5.9. For any
![]() $i,j,k,l\in \{1,\dots ,m, o\}$
, the following open WDVV equation holds:
$i,j,k,l\in \{1,\dots ,m, o\}$
, the following open WDVV equation holds:
where the summation index
![]() $\mu $
runs through
$\mu $
runs through
![]() $1, \dots , m, o$
.
$1, \dots , m, o$
.
Proof. Recall that the vector potential
![]() $\overline {F}$
consists of functions that are independent of
$\overline {F}$
consists of functions that are independent of
![]() $t^o$
. Thus, the two sides of (17) are zero if at least one of
$t^o$
. Thus, the two sides of (17) are zero if at least one of
![]() $i, k, l$
is o. For the remaining case
$i, k, l$
is o. For the remaining case
![]() $i, k, l \in \{1, \dots , m\}$
, first note that the term in (17) corresponding to
$i, k, l \in \{1, \dots , m\}$
, first note that the term in (17) corresponding to
![]() $\mu = o$
is again zero. Then the case
$\mu = o$
is again zero. Then the case
![]() $j \in \{1, \dots , m\}$
follows from identities (Ia), (Ib) and (Ic) of Proposition 4.4, and the case
$j \in \{1, \dots , m\}$
follows from identities (Ia), (Ib) and (Ic) of Proposition 4.4, and the case
![]() $j = o$
follows from identities (IIa) and (IIb).
$j = o$
follows from identities (IIa) and (IIb).
5.2.3 The flat formal F-manifold
Let
![]() $\nabla $
be the flat connection on
$\nabla $
be the flat connection on
![]() $\mathcal {T}_{\hat {H}_2}$
under which
$\mathcal {T}_{\hat {H}_2}$
under which
![]() $\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m}$
,
$\frac {\partial }{\partial t^1},\dots ,\frac {\partial }{\partial t^m}$
,
![]() $\frac {\partial }{\partial t^o}$
are flat. Moreover, we define the following product.
$\frac {\partial }{\partial t^o}$
are flat. Moreover, we define the following product.
Definition 5.10. For any
![]() $i,j\in \{1,\dots ,m, o\}$
, define the product
$i,j\in \{1,\dots ,m, o\}$
, define the product
![]() $\frac {\partial }{\partial t^i}\star _t\frac {\partial }{\partial t^j}$
on
$\frac {\partial }{\partial t^i}\star _t\frac {\partial }{\partial t^j}$
on
![]() $\mathcal {T}_{\hat {H}_2}$
by
$\mathcal {T}_{\hat {H}_2}$
by
where the summation index k runs through
![]() $1, \dots , m, o$
.
$1, \dots , m, o$
.
Since the components of the vector potential
![]() $\overline {F}$
are independent of
$\overline {F}$
are independent of
![]() $t^o$
, the above definition implies that
$t^o$
, the above definition implies that
for any
![]() $i = 1, \dots , m, o$
. Thus,
$i = 1, \dots , m, o$
. Thus,
![]() $\frac {\partial }{\partial t^o}$
is nilpotent. Moreover, the product
$\frac {\partial }{\partial t^o}$
is nilpotent. Moreover, the product
![]() $\star _t$
does not admit an identity field, which means that the induced structure on
$\star _t$
does not admit an identity field, which means that the induced structure on
![]() $\hat {H}_2$
will be an formal F-manifold without unit. This is different from the case studied by [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] (see Theorem 1.3), and the difference is reflected by that our
$\hat {H}_2$
will be an formal F-manifold without unit. This is different from the case studied by [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] (see Theorem 1.3), and the difference is reflected by that our
![]() $F^o = F_{0,1}^{X,(L, f)}$
is supported on the ideal of
$F^o = F_{0,1}^{X,(L, f)}$
is supported on the ideal of
![]() $\Lambda _{X,L}$
generated by
$\Lambda _{X,L}$
generated by
![]() $\mathsf {X}_0$
while the disk potential of [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] has a constant term. The difference is discussed from the perspective of open WDVV equations in Remark 4.5.
$\mathsf {X}_0$
while the disk potential of [Reference Horev and Solomon26, Reference Solomon and Tukachinsky43] has a constant term. The difference is discussed from the perspective of open WDVV equations in Remark 4.5.
Summarizing the above, we arrive at the following result.
Theorem 5.11. The tuple
![]() $(\hat {H}_2, \nabla , \star _t)$
is a flat formal F-manifold without the unit over
$(\hat {H}_2, \nabla , \star _t)$
is a flat formal F-manifold without the unit over
![]() $\Lambda _{X,L}^{T_f}$
in which the
$\Lambda _{X,L}^{T_f}$
in which the
![]() $t^o$
-direction is nilpotent.
$t^o$
-direction is nilpotent.
Remark 5.12. The flat formal F-manifold
![]() $\hat {H}_2$
is a rank-1 extension of the formal Frobenius manifold
$\hat {H}_2$
is a rank-1 extension of the formal Frobenius manifold
![]() $\hat {H}_X^f$
(defined in (14)) in the sense of, for example, [Reference Alcolado1, Chapter 3], [Reference Basalaev and Buryak4, Section 4]. In other words, there is a surjective homomorphism from the global algebra of
$\hat {H}_X^f$
(defined in (14)) in the sense of, for example, [Reference Alcolado1, Chapter 3], [Reference Basalaev and Buryak4, Section 4]. In other words, there is a surjective homomorphism from the global algebra of
![]() $\hat {H}_2$
to that of
$\hat {H}_2$
to that of
![]() $\hat {H}_X^f$
whose kernel is the rank-1 algebra over
$\hat {H}_X^f$
whose kernel is the rank-1 algebra over
![]() $\Lambda _{X,L}^{T_f}$
generated by the nilpotent element
$\Lambda _{X,L}^{T_f}$
generated by the nilpotent element
![]() $\frac {\partial }{\partial t^o}$
.
$\frac {\partial }{\partial t^o}$
.
A Deferred proofs
A.1 Proof of Theorem 3.1
We consider the contributions of individual effective classes to the Gromov-Witten potential
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
of
$F_0^{\widetilde {X},\widetilde {T}'}$
of
![]() $\widetilde {X}$
. Let
$\widetilde {X}$
. Let
![]() $\widetilde {\beta } = (\beta , d) \in E(\widetilde {X})$
, which by Section 2.4 corresponds to an effective class in
$\widetilde {\beta } = (\beta , d) \in E(\widetilde {X})$
, which by Section 2.4 corresponds to an effective class in
![]() $E(X,L)$
. By (7), we consider the computation of the closed invariant
$E(X,L)$
. By (7), we consider the computation of the closed invariant
by localization as detailed in [Reference Liu and Yu33, Section 3.5], [Reference Liu and Yu34, Section 3.5] and adopt the notations there. Components of the
![]() $\widetilde {T}'$
-fixed locus of the moduli space
$\widetilde {T}'$
-fixed locus of the moduli space
![]() $\overline {\mathcal {M}}_{0, n}(\widetilde {X}, \widetilde {\beta })$
are indexed by the set
$\overline {\mathcal {M}}_{0, n}(\widetilde {X}, \widetilde {\beta })$
are indexed by the set
![]() $\Gamma _{0, n}(\widetilde {X}, \widetilde {\beta })$
of decorated graphs (see [Reference Liu and Yu33, Section 3.1], [Reference Liu and Yu34, Section 3.2]). We have
$\Gamma _{0, n}(\widetilde {X}, \widetilde {\beta })$
of decorated graphs (see [Reference Liu and Yu33, Section 3.1], [Reference Liu and Yu34, Section 3.2]). We have
 $$ \begin{align} \langle \tilde{t}, \dots, \tilde{t} \rangle^{\widetilde{X},\widetilde{T}'}_{0,n,\widetilde{\beta}} = \sum_{\widetilde{\Gamma} \in \Gamma_{0,n}(\widetilde{X}, \widetilde{\beta})} \widetilde{C}_{\widetilde{\Gamma}}, \end{align} $$
$$ \begin{align} \langle \tilde{t}, \dots, \tilde{t} \rangle^{\widetilde{X},\widetilde{T}'}_{0,n,\widetilde{\beta}} = \sum_{\widetilde{\Gamma} \in \Gamma_{0,n}(\widetilde{X}, \widetilde{\beta})} \widetilde{C}_{\widetilde{\Gamma}}, \end{align} $$
where
![]() $\widetilde {C}_{\widetilde {\Gamma }}$
is the contribution of the component indexed by
$\widetilde {C}_{\widetilde {\Gamma }}$
is the contribution of the component indexed by
![]() $\widetilde {\Gamma }$
.
$\widetilde {\Gamma }$
.
Let
![]() $\widetilde {\Gamma } = (\Gamma , \vec {f}, \vec {d}, \vec {s}) \in \Gamma _{0,n}(\widetilde {X}, \widetilde {\beta })$
. As in [Reference Liu and Yu34, Section 4.3], let
$\widetilde {\Gamma } = (\Gamma , \vec {f}, \vec {d}, \vec {s}) \in \Gamma _{0,n}(\widetilde {X}, \widetilde {\beta })$
. As in [Reference Liu and Yu34, Section 4.3], let
and
![]() $c_0$
denote the number of connected components of the subgraph of
$c_0$
denote the number of connected components of the subgraph of
![]() $\Gamma $
induced on
$\Gamma $
induced on
![]() $V_0$
. We may assume that
$V_0$
. We may assume that
![]() $c_0 \ge 1$
, since otherwise,
$c_0 \ge 1$
, since otherwise,
![]() $\widetilde {\Gamma }$
represents a constant map to the fixed point
$\widetilde {\Gamma }$
represents a constant map to the fixed point
![]() $\widetilde {p}_{m+1}$
Footnote
5
and thus
$\widetilde {p}_{m+1}$
Footnote
5
and thus
![]() $\widetilde {C}_{\widetilde {\Gamma }} = 0$
. By the proof of [Reference Liu and Yu34, Lemma 4.4], the total power of
$\widetilde {C}_{\widetilde {\Gamma }} = 0$
. By the proof of [Reference Liu and Yu34, Lemma 4.4], the total power of
![]() $\mathsf {u}_4$
in
$\mathsf {u}_4$
in
![]() $\widetilde {C}_{\widetilde {\Gamma }}$
is
$\widetilde {C}_{\widetilde {\Gamma }}$
is
Equality holds if and only if
![]() $E_2 = \emptyset $
and
$E_2 = \emptyset $
and
![]() $V_0 = V(\Gamma )$
, which happens if and only if
$V_0 = V(\Gamma )$
, which happens if and only if
![]() $d = 0$
. Therefore,
$d = 0$
. Therefore,
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
has at most a simple pole along
$F_0^{\widetilde {X},\widetilde {T}'}$
has at most a simple pole along
![]() $\mathsf {u}_4$
and the residue
$\mathsf {u}_4$
and the residue
![]() $\widetilde {A}$
is supported on the Novikov variables
$\widetilde {A}$
is supported on the Novikov variables
![]() $\{\widetilde {Q}^{\iota _*(\beta )}: \beta \in E(X)\}$
and is independent of
$\{\widetilde {Q}^{\iota _*(\beta )}: \beta \in E(X)\}$
and is independent of
![]() $t^{m+1}$
. Part (b) of the theorem follows from the following result.
$t^{m+1}$
. Part (b) of the theorem follows from the following result.
Lemma A.1. For
![]() $\widetilde {\beta } = (\beta , 0)$
, we have
$\widetilde {\beta } = (\beta , 0)$
, we have
Proof. We consider the contributions from decorated graphs as in (18). In the case
![]() $\widetilde {\beta } = \iota _*(\beta )$
, any
$\widetilde {\beta } = \iota _*(\beta )$
, any
![]() $\widetilde {\Gamma } \in \Gamma _{0, n}(\widetilde {X}, \widetilde {\beta })$
(with
$\widetilde {\Gamma } \in \Gamma _{0, n}(\widetilde {X}, \widetilde {\beta })$
(with
![]() $c_0 \neq 0$
) naturally corresponds to a decorated graph in
$c_0 \neq 0$
) naturally corresponds to a decorated graph in
![]() $\Gamma _{0, n}(X, \beta )$
; that is, it represents stable maps which factor through
$\Gamma _{0, n}(X, \beta )$
; that is, it represents stable maps which factor through
![]() $X \subset \widetilde {X}$
. The lemma then follows directly from the comparison of localization contributions as in the proof of [Reference Liu and Yu34, Lemma 4.2]. Note from (4) that
$X \subset \widetilde {X}$
. The lemma then follows directly from the comparison of localization contributions as in the proof of [Reference Liu and Yu34, Lemma 4.2]. Note from (4) that
![]() $\tilde {t} \big |_{\widetilde {p}_i} = t \big |_{p_i}$
for
$\tilde {t} \big |_{\widetilde {p}_i} = t \big |_{p_i}$
for
![]() $i = 1, \dots , m$
.
$i = 1, \dots , m$
.
Now we consider the case
![]() $d>0$
which corresponds to the part of
$d>0$
which corresponds to the part of
![]() $F_0^{\widetilde {X},\widetilde {T}'}$
that does not have a pole along
$F_0^{\widetilde {X},\widetilde {T}'}$
that does not have a pole along
![]() $\mathsf {u}_4$
. By the divisor equation, we have
$\mathsf {u}_4$
. By the divisor equation, we have
Similar to (18), we consider the localization computation of this invariant as a sum of contributions from decorated graphs:
 $$ \begin{align} \langle \tilde{t}, \dots, \tilde{t}, \widetilde{D} \rangle^{\widetilde{X},\widetilde{T}'}_{0,n+1,\widetilde{\beta}} = \sum_{\widetilde{\Gamma} \in \Gamma_{0,n+1}(\widetilde{X}, \widetilde{\beta})} \widetilde{C}_{\widetilde{\Gamma}}, \end{align} $$
$$ \begin{align} \langle \tilde{t}, \dots, \tilde{t}, \widetilde{D} \rangle^{\widetilde{X},\widetilde{T}'}_{0,n+1,\widetilde{\beta}} = \sum_{\widetilde{\Gamma} \in \Gamma_{0,n+1}(\widetilde{X}, \widetilde{\beta})} \widetilde{C}_{\widetilde{\Gamma}}, \end{align} $$
where by an abuse of notation,
![]() $\widetilde {C}_{\widetilde {\Gamma }}$
denotes the contribution of
$\widetilde {C}_{\widetilde {\Gamma }}$
denotes the contribution of
![]() $\widetilde {\Gamma } \in \Gamma _{0,n+1}(\widetilde {X}, \widetilde {\beta })$
. We study the poles of
$\widetilde {\Gamma } \in \Gamma _{0,n+1}(\widetilde {X}, \widetilde {\beta })$
. We study the poles of
![]() $\widetilde {C}_{\widetilde {\Gamma }}$
along
$\widetilde {C}_{\widetilde {\Gamma }}$
along
![]() $\mathsf {u}_2 - f\mathsf {u}_1$
or
$\mathsf {u}_2 - f\mathsf {u}_1$
or
![]() $\mathsf {u}_2 - f\mathsf {u}_1 - \mathsf {u}_4$
. We assume below that
$\mathsf {u}_2 - f\mathsf {u}_1 - \mathsf {u}_4$
. We assume below that
![]() $f \in \mathbb {Z}$
is generic with respect to the curve class
$f \in \mathbb {Z}$
is generic with respect to the curve class
![]() $\widetilde {\beta }$
. Eventually, the argument in [Reference Liu and Yu34, Section 4.4] will enable us to extend the proof to all
$\widetilde {\beta }$
. Eventually, the argument in [Reference Liu and Yu34, Section 4.4] will enable us to extend the proof to all
![]() $f \in \mathbb {Z}$
.
$f \in \mathbb {Z}$
.
Note that
![]() $E_2 \neq \emptyset $
when
$E_2 \neq \emptyset $
when
![]() $d>0$
. By the computations in the proof of [Reference Liu and Yu34, Lemma 4.6], we can write
$d>0$
. By the computations in the proof of [Reference Liu and Yu34, Lemma 4.6], we can write
 $$ \begin{align*}\widetilde{C}_{\widetilde{\Gamma}} = \begin{cases} \frac{\widetilde{\mathbf{w}}(\widetilde{\tau}_3, \widetilde{\sigma}_0)^{|E_2|-1}}{\widetilde{\mathbf{w}}(\widetilde{\tau}_2, \widetilde{\sigma}_0)} \widetilde{c}_{\widetilde{\Gamma}} & \text{if } f \ge 0\\[4pt] \frac{\widetilde{\mathbf{w}}(\widetilde{\tau}_2, \widetilde{\sigma}_0)^{|E_2|-1}}{\widetilde{\mathbf{w}}(\widetilde{\tau}_3, \widetilde{\sigma}_0)}\widetilde{c}_{\widetilde{\Gamma}} & \text{if } f < 0 \end{cases} = \frac{1}{\mathsf{v}}\widetilde{b}_{\widetilde{\Gamma}} + \frac{\mathsf{u}_4}{\mathsf{v}}\widetilde{c}_{\widetilde{\Gamma},1} + \widetilde{c}_{\widetilde{\Gamma},2}, \end{align*} $$
$$ \begin{align*}\widetilde{C}_{\widetilde{\Gamma}} = \begin{cases} \frac{\widetilde{\mathbf{w}}(\widetilde{\tau}_3, \widetilde{\sigma}_0)^{|E_2|-1}}{\widetilde{\mathbf{w}}(\widetilde{\tau}_2, \widetilde{\sigma}_0)} \widetilde{c}_{\widetilde{\Gamma}} & \text{if } f \ge 0\\[4pt] \frac{\widetilde{\mathbf{w}}(\widetilde{\tau}_2, \widetilde{\sigma}_0)^{|E_2|-1}}{\widetilde{\mathbf{w}}(\widetilde{\tau}_3, \widetilde{\sigma}_0)}\widetilde{c}_{\widetilde{\Gamma}} & \text{if } f < 0 \end{cases} = \frac{1}{\mathsf{v}}\widetilde{b}_{\widetilde{\Gamma}} + \frac{\mathsf{u}_4}{\mathsf{v}}\widetilde{c}_{\widetilde{\Gamma},1} + \widetilde{c}_{\widetilde{\Gamma},2}, \end{align*} $$
where each of
![]() $\widetilde {c}_{\widetilde {\Gamma }}, \widetilde {b}_{\widetilde {\Gamma }}, \widetilde {c}_{\widetilde {\Gamma },1}, \widetilde {c}_{\widetilde {\Gamma },2}$
has a well-defined weight restriction to
$\widetilde {c}_{\widetilde {\Gamma }}, \widetilde {b}_{\widetilde {\Gamma }}, \widetilde {c}_{\widetilde {\Gamma },1}, \widetilde {c}_{\widetilde {\Gamma },2}$
has a well-defined weight restriction to
![]() $\mathsf {u}_4 = 0, \mathsf {u}_2 - f\mathsf {u}_1 = 0$
. Moreover,
$\mathsf {u}_4 = 0, \mathsf {u}_2 - f\mathsf {u}_1 = 0$
. Moreover,
![]() $\widetilde {b}_{\widetilde {\Gamma }}$
is nonzero only if
$\widetilde {b}_{\widetilde {\Gamma }}$
is nonzero only if
![]() $|E_2|=1$
, in which case, [Reference Liu and Yu34, Lemma 4.2] implies that
$|E_2|=1$
, in which case, [Reference Liu and Yu34, Lemma 4.2] implies that
![]() $\widetilde {b}_{\widetilde {\Gamma }}$
(or the graph
$\widetilde {b}_{\widetilde {\Gamma }}$
(or the graph
![]() $\widetilde {\Gamma }$
) contributes to the localization computation of a corresponding disk invariant of
$\widetilde {\Gamma }$
) contributes to the localization computation of a corresponding disk invariant of
![]() $(X,L,f)$
. More formally, and combining the analysis over all decorated graphs, we have the following lemma which is a direct consequence of [Reference Liu and Yu34, Lemma 4.2].
$(X,L,f)$
. More formally, and combining the analysis over all decorated graphs, we have the following lemma which is a direct consequence of [Reference Liu and Yu34, Lemma 4.2].
Lemma A.2. For
![]() $\widetilde {\beta } = (\beta , d)$
with
$\widetilde {\beta } = (\beta , d)$
with
![]() $d> 0$
, we can write
$d> 0$
, we can write
where each of
![]() $\widetilde {b}, \widetilde {c}_1, \widetilde {c}_2$
has a well-defined weight restriction to
$\widetilde {b}, \widetilde {c}_1, \widetilde {c}_2$
has a well-defined weight restriction to
![]() $\mathsf {u}_4 = 0, \mathsf {u}_2 - f\mathsf {u}_1 = 0$
and
$\mathsf {u}_4 = 0, \mathsf {u}_2 - f\mathsf {u}_1 = 0$
and
Lemma A.2 implies part (c) of Theorem 3.1 and completes the proof.
Acknowledgements
The authors wish to thank Alexandr Buryak, Bohan Fang, Sheel Ganatra, Chiu-Chu Melissa Liu, Jake Solomon, Junwu Tu, Ke Zhang and Yang Zhou for useful discussions and constructive feedback. The authors also wish to thank the hospitality of the Simons Center for Geometry and Physics during the 2023 Simons Math Summer Workshop where part of this work was completed.
Competing interest
The authors have no competing interest to declare.
Financial support
The work of the second named author is partially supported by NSFC grant No. 11701315.