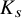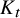1 Introduction
Ramsey theory, initially explored by Ramsey [Reference Ramsey32] in 1930, stands as a pivotal branch of combinatorics. It seeks to tackle a fundamental question: what is the minimum size required to guarantee the existence of a well-defined substructure within a larger, often chaotic, set or system? One of the most renowned results in Ramsey theory is Ramsey’s theorem, which asserts that if n is large enough in terms of k, then no matter how one colors the edges of a complete graph of order n using two colors, there will always exist a monochromatic complete subgraph
![]() $K_k$
.
$K_k$
.
In 1941, Turán [Reference Turán37] proposed and solved the following problem: what is the maximum number of edges that a graph G of order n can have without containing a complete graph
![]() $K_k$
? He also proved that the value is attained only by the balanced complete
$K_k$
? He also proved that the value is attained only by the balanced complete
![]() $(k-1)$
-partite graph, now known as the Turán graph
$(k-1)$
-partite graph, now known as the Turán graph
![]() $T_{k-1}(n)$
. Subsequently, a new branch of extremal combinatorics named after him emerged: Turán-type problems. Formally, we define the generalized Turán function
$T_{k-1}(n)$
. Subsequently, a new branch of extremal combinatorics named after him emerged: Turán-type problems. Formally, we define the generalized Turán function
![]() $\mathrm {ex}(n, H_1, H_2)$
as the maximum possible number of copies of
$\mathrm {ex}(n, H_1, H_2)$
as the maximum possible number of copies of
![]() $H_1$
in an n-vertex
$H_1$
in an n-vertex
![]() $H_2$
-free graph. There has been extensive research on this function. When
$H_2$
-free graph. There has been extensive research on this function. When
![]() $H_1\cong K_2$
, Erdős, Stone, and Simonovits (see [Reference Erdős and Simonovits14, Reference Erdős and Stone15]) gave an asymptotically satisfactory solution for all graphs
$H_1\cong K_2$
, Erdős, Stone, and Simonovits (see [Reference Erdős and Simonovits14, Reference Erdős and Stone15]) gave an asymptotically satisfactory solution for all graphs
![]() $H_2$
, and Erdős [Reference Erdős13] additionally determined
$H_2$
, and Erdős [Reference Erdős13] additionally determined
![]() $\mathrm {ex}(n, K_s, K_t)$
for all
$\mathrm {ex}(n, K_s, K_t)$
for all
![]() $t>s\geq 3$
. More recently, Alon and Shikhelman [Reference Alon and Shikhelman1] systematically studied
$t>s\geq 3$
. More recently, Alon and Shikhelman [Reference Alon and Shikhelman1] systematically studied
![]() $\mathrm {ex}(n, H_1, H_2)$
for other graphs
$\mathrm {ex}(n, H_1, H_2)$
for other graphs
![]() $H_1$
, and there have been a number of results in this direction (see e.g., [Reference Beke and Janzer9, Reference Gao, Wu and Xue19, Reference Gishboliner and Shapira20, Reference Ma and Qiu30, Reference Morrison, Nir, Norin, Rzążewski and Wesolek31]).
$H_1$
, and there have been a number of results in this direction (see e.g., [Reference Beke and Janzer9, Reference Gao, Wu and Xue19, Reference Gishboliner and Shapira20, Reference Ma and Qiu30, Reference Morrison, Nir, Norin, Rzążewski and Wesolek31]).
In this paper, we study the following extremal quantity which mixes Ramsey theory with Turán-type problems. Define the generalized Ramsey–Turán number
![]() $\mathrm {RT}(n,H_1,H_2,\ell )$
to be the maximum number of copies of
$\mathrm {RT}(n,H_1,H_2,\ell )$
to be the maximum number of copies of
![]() $H_1$
in an n-vertex
$H_1$
in an n-vertex
![]() $H_2$
-free graph G with independence number
$H_2$
-free graph G with independence number
![]() $\alpha (G)< \ell $
. We remark that the existence of such a graph G is controlled by the Ramsey number
$\alpha (G)< \ell $
. We remark that the existence of such a graph G is controlled by the Ramsey number
![]() $R(H_2,K_{\ell })$
, which is defined to be the least N such that every graph G on N vertices contains either a subgraph isomorphic to
$R(H_2,K_{\ell })$
, which is defined to be the least N such that every graph G on N vertices contains either a subgraph isomorphic to
![]() $H_2$
or an independent set of size
$H_2$
or an independent set of size
![]() $\ell $
. This quantity is also inherently related to the generalized Turán function; indeed, we have
$\ell $
. This quantity is also inherently related to the generalized Turán function; indeed, we have
![]() $\mathrm {ex}(n, H_1, H_2)=\mathrm {RT}(n,H_1,H_2,n+1)$
.
$\mathrm {ex}(n, H_1, H_2)=\mathrm {RT}(n,H_1,H_2,n+1)$
.
This beautiful way of combining Ramsey theory with Turán-type problems was first proposed in the late 1960s by Sós [Reference Sós34], who investigated
![]() $\mathrm {RT}(n,K_2,H,\ell )$
. The most studied case is when the independence number is sublinear:
$\mathrm {RT}(n,K_2,H,\ell )$
. The most studied case is when the independence number is sublinear:
![]() $\ell =o(n)$
. To eliminate minor fluctuations caused by small values of n, one usually considers the asymptotic behavior via the Ramsey–Turán density function,
$\ell =o(n)$
. To eliminate minor fluctuations caused by small values of n, one usually considers the asymptotic behavior via the Ramsey–Turán density function,

It is not hard to see that the above limits exist. Then define
![]() $\mathrm {RT}(n,K_s,K_t,o(n))=\varrho _s(K_t){n\choose s}+o(n^s)$
. We say an n-vertex
$\mathrm {RT}(n,K_s,K_t,o(n))=\varrho _s(K_t){n\choose s}+o(n^s)$
. We say an n-vertex
![]() $K_t$
-free graph G with
$K_t$
-free graph G with
![]() $\alpha (G)=o(n)$
is an (asymptotic) extremal graph if its
$\alpha (G)=o(n)$
is an (asymptotic) extremal graph if its
![]() $K_s$
-density attains
$K_s$
-density attains
![]() $\varrho _s(K_t)$
.
$\varrho _s(K_t)$
.
When
![]() $s=2$
, the Ramsey–Turán density has now been completely determined. It was, however, a bumpy road. In 1969, Erdős and Sós [Reference Erdős and Sós17] showed that
$s=2$
, the Ramsey–Turán density has now been completely determined. It was, however, a bumpy road. In 1969, Erdős and Sós [Reference Erdős and Sós17] showed that
![]() $\varrho _2(K_{2k+1})=\frac {k-1}{k}$
. The even cliques case became significantly more challenging. As a first application of the celebrated regularity lemma, Szemerédi [Reference Szemerédi35] in 1972 proved that
$\varrho _2(K_{2k+1})=\frac {k-1}{k}$
. The even cliques case became significantly more challenging. As a first application of the celebrated regularity lemma, Szemerédi [Reference Szemerédi35] in 1972 proved that
![]() $\varrho _2(K_4)\le \frac {1}{4}$
, and in 1976 Bollobás and Erdős [Reference Bollobás and Erdős10] obtained a matching lower bound
$\varrho _2(K_4)\le \frac {1}{4}$
, and in 1976 Bollobás and Erdős [Reference Bollobás and Erdős10] obtained a matching lower bound
![]() $\varrho _2(K_4)\ge \frac {1}{4}$
via an astonishing geometric construction (now called the Bollobás–Erdős graph). Eventually, in 1983, Erdős, Hajnal, Sós and Szemerédi [Reference Erdős, Hajnal, Sós and Szemerédi16] completed the picture, showing that
$\varrho _2(K_4)\ge \frac {1}{4}$
via an astonishing geometric construction (now called the Bollobás–Erdős graph). Eventually, in 1983, Erdős, Hajnal, Sós and Szemerédi [Reference Erdős, Hajnal, Sós and Szemerédi16] completed the picture, showing that
![]() $\varrho _2(K_{2k})=\frac {3k-5}{3k-2}$
for all
$\varrho _2(K_{2k})=\frac {3k-5}{3k-2}$
for all
![]() $k\geq 2$
. In fact, they proved a much stronger result showing that extremal graphs for
$k\geq 2$
. In fact, they proved a much stronger result showing that extremal graphs for
![]() $\varrho _2(K_t)$
exhibit the following periodic behavior:
$\varrho _2(K_t)$
exhibit the following periodic behavior:
-
(⋆) Let
 $t=2p+r\ge 4$
, where
$t=2p+r\ge 4$
, where
 $r\in \{0,1\}$
. There is an extremal graph G for
$r\in \{0,1\}$
. There is an extremal graph G for
 $\varrho _2(K_t)$
whose vertex set can be partitioned into
$\varrho _2(K_t)$
whose vertex set can be partitioned into
 $V_1\cup \cdots \cup V_p$
satisfying (i)
$V_1\cup \cdots \cup V_p$
satisfying (i)
 $G[V_1,V_2]$
has edge density
$G[V_1,V_2]$
has edge density
 $\frac {r+1}{2}-o(1)$
; (ii) every other
$\frac {r+1}{2}-o(1)$
; (ii) every other
 $G[V_i,V_j]$
has edge density
$G[V_i,V_j]$
has edge density
 $1-o(1)$
; and (iii) each
$1-o(1)$
; and (iii) each
 $G[V_i]$
has edge density
$G[V_i]$
has edge density
 $o(1)$
.
$o(1)$
.
In other words, the extremal structure depends on the parity r of t and evolves as follows: the density of
![]() $G[V_1,V_2]$
increases as the parity r increases; and whenever t increases by
$G[V_1,V_2]$
increases as the parity r increases; and whenever t increases by
![]() $2$
, a new part is added and joined almost completely to all previous parts (depicted in the first row of Table 1). For more recent developments of the
$2$
, a new part is added and joined almost completely to all previous parts (depicted in the first row of Table 1). For more recent developments of the
![]() $s=2$
case and related variations, we refer the interested reader to [Reference Balogh, Bradac and Lidický2, Reference Balogh, Chen, McCourt and Murley3, Reference Balogh, Hu and Simonovits4, Reference Balogh and Lenz5, Reference Balogh, Liu and Sharifzadeh6, Reference Balogh, Molla and Sharifzadeh8, Reference Chang, Han, Kim, Wang and Yang11, Reference Fox, Loh and Zhao18, Reference Han, Hu, Wang and Yang21, Reference Han, Morris, Wang and Yang22, Reference Hu and Lin23, Reference Kim, Kim and Liu24, Reference Knierim and Su25, Reference Liu, Reiher, Sharifzadeh and Staden26, Reference Liu and Li27, Reference Łuczak, Polcyn and Reiher28, Reference Lüders and Reiher29].
$s=2$
case and related variations, we refer the interested reader to [Reference Balogh, Bradac and Lidický2, Reference Balogh, Chen, McCourt and Murley3, Reference Balogh, Hu and Simonovits4, Reference Balogh and Lenz5, Reference Balogh, Liu and Sharifzadeh6, Reference Balogh, Molla and Sharifzadeh8, Reference Chang, Han, Kim, Wang and Yang11, Reference Fox, Loh and Zhao18, Reference Han, Hu, Wang and Yang21, Reference Han, Morris, Wang and Yang22, Reference Hu and Lin23, Reference Kim, Kim and Liu24, Reference Knierim and Su25, Reference Liu, Reiher, Sharifzadeh and Staden26, Reference Liu and Li27, Reference Łuczak, Polcyn and Reiher28, Reference Lüders and Reiher29].
Table 1 Conjectured periodic extremal structure. Black edges have density 1 and red edges have density 1/2.

Balogh, Liu, and Sharifzadeh [Reference Balogh, Liu and Sharifzadeh6] recently initiated the study of the general case
![]() $s\ge 3$
, which turns out to be much more difficult and delicate than the
$s\ge 3$
, which turns out to be much more difficult and delicate than the
![]() $s=2$
case. Note that
$s=2$
case. Note that
![]() $\varrho _{s}(K_{s+1})=0$
: in any n-vertex
$\varrho _{s}(K_{s+1})=0$
: in any n-vertex
![]() $K_{s+1}$
-free graph with independence number
$K_{s+1}$
-free graph with independence number
![]() $o(n)$
, each copy of
$o(n)$
, each copy of
![]() $K_{s-1}$
lies in
$K_{s-1}$
lies in
![]() $o(n)$
copies of
$o(n)$
copies of
![]() $K_s$
. Balogh, Liu, and Sharifzadeh [Reference Balogh, Liu and Sharifzadeh6] determined the first non-trivial cases
$K_s$
. Balogh, Liu, and Sharifzadeh [Reference Balogh, Liu and Sharifzadeh6] determined the first non-trivial cases
![]() $\varrho _{3}(K_{t})$
and
$\varrho _{3}(K_{t})$
and
![]() $\varrho _{s}(K_{s+2})$
, and made a conjecture predicting the general case. We find it more convenient to work with the following definition, which helps reformulate their conjecture.
$\varrho _{s}(K_{s+2})$
, and made a conjecture predicting the general case. We find it more convenient to work with the following definition, which helps reformulate their conjecture.
Definition 1.1. Given integers
![]() $b\geq a\ge 1$
, a graph G admits a
$b\geq a\ge 1$
, a graph G admits a
![]() $(b,a)$
-partition if its vertex set has a partition
$(b,a)$
-partition if its vertex set has a partition
![]() $V=V_1\cup \cdots \cup V_a$
satisfying the following for
$V=V_1\cup \cdots \cup V_a$
satisfying the following for
![]() $b_1,\ldots ,b_a\in \{\lceil \frac {b}{a}\rceil ,\lfloor \frac {b}{a}\rfloor \}$
with
$b_1,\ldots ,b_a\in \{\lceil \frac {b}{a}\rceil ,\lfloor \frac {b}{a}\rfloor \}$
with
![]() $\sum _{i=1}^a b_i = b$
:
$\sum _{i=1}^a b_i = b$
:
-
(1) For every distinct
 $i,j\in [a]$
,
$i,j\in [a]$
,
 $G[V_i,V_j]$
has edge density
$G[V_i,V_j]$
has edge density
 $1-o(1)$
; and
$1-o(1)$
; and -
(2) For every
 $i\in [a]$
,
$i\in [a]$
,
 $V_i$
admits an equipartition
$V_i$
admits an equipartition
 $V_i^1\cup \cdots \cup V_i^{b_i}$
such that
$V_i^1\cup \cdots \cup V_i^{b_i}$
such that
 $G[V_i^j]$
has density
$G[V_i^j]$
has density
 $o(1)$
for all
$o(1)$
for all
 $j\in [b_i]$
and
$j\in [b_i]$
and
 $G[V_i^j,V_i^{k}]$
has density
$G[V_i^j,V_i^{k}]$
has density
 $\frac {1}{2}-o(1)$
for all distinct
$\frac {1}{2}-o(1)$
for all distinct
 $j,k\in [b_i]$
.
$j,k\in [b_i]$
.
For instance, if
![]() $a=b=p$
then each
$a=b=p$
then each
![]() $b_i=1$
, so an n-vertex graph admits a
$b_i=1$
, so an n-vertex graph admits a
![]() $(p,p)$
-partition if and only if it has edit-distance
$(p,p)$
-partition if and only if it has edit-distance
![]() $o(n^2)$
to the Turán graph
$o(n^2)$
to the Turán graph
![]() $T_p(n)$
.
$T_p(n)$
.
Conjecture 1.2 [Reference Balogh, Liu and Sharifzadeh6]
Given integers
![]() $t-2\ge s\ge 3$
, there is an extremal graph for
$t-2\ge s\ge 3$
, there is an extremal graph for
![]() $\varrho _{s}(K_t)$
which admits
$\varrho _{s}(K_t)$
which admits
-
(i) an
 $(s,t-1-s)$
-partition if
$(s,t-1-s)$
-partition if
 $s+2\le t\le 2s-1$
, or
$s+2\le t\le 2s-1$
, or -
(ii) a
 $(\lfloor \frac {t}{2}\rfloor ,t-1-\lfloor \frac {t}{2}\rfloor )$
-partition if
$(\lfloor \frac {t}{2}\rfloor ,t-1-\lfloor \frac {t}{2}\rfloor )$
-partition if
 $t\ge 2s$
.
$t\ge 2s$
.
The preceding conjecture can be better understood, using the language of Definition 1.1, as follows. For every
![]() $t=2p+r\ge 4$
with
$t=2p+r\ge 4$
with
![]() $r\in \{0,1\}$
, the periodic behavior of
$r\in \{0,1\}$
, the periodic behavior of
![]() $\varrho _2(K_t)$
in
$\varrho _2(K_t)$
in
![]() $(\star )$
can be rephrased as ‘an extremal graph for
$(\star )$
can be rephrased as ‘an extremal graph for
![]() $\varrho _2(K_t)$
admits a
$\varrho _2(K_t)$
admits a
![]() $(p,p-1+r)$
-partition’, which is precisely the statement of Conjecture 1.2(ii) when
$(p,p-1+r)$
-partition’, which is precisely the statement of Conjecture 1.2(ii) when
![]() $s=2$
. Thus, Conjecture 1.2 speculates that similar periodic behavior occurs at the threshold
$s=2$
. Thus, Conjecture 1.2 speculates that similar periodic behavior occurs at the threshold
![]() $t\ge 2s$
for all
$t\ge 2s$
for all
![]() $s\ge 3$
(see Table 1). Further supporting this prediction, it was proved in [Reference Balogh, Liu and Sharifzadeh6] that Conjecture 1.2 holds for
$s\ge 3$
(see Table 1). Further supporting this prediction, it was proved in [Reference Balogh, Liu and Sharifzadeh6] that Conjecture 1.2 holds for
![]() $s=3$
.
$s=3$
.
We present infinitely many counterexamples showing that Conjecture 1.2 is false in general. The smallest counterexamples we observe are
![]() $s=5$
and
$s=5$
and
![]() $t\in \{10,11\}$
(see Figure 2). On the positive side, we prove that the predicted periodic behavior does eventually occur when
$t\in \{10,11\}$
(see Figure 2). On the positive side, we prove that the predicted periodic behavior does eventually occur when
![]() $t\gg s$
for all
$t\gg s$
for all
![]() $s\ge 3$
.
$s\ge 3$
.
Theorem 1.3. Conjecture 1.2 is false when
![]() $2s\leq t\leq 2.08s$
for sufficiently large s. Given
$2s\leq t\leq 2.08s$
for sufficiently large s. Given
![]() $t-2\geq s\geq 3$
, Conjecture 1.2 is true if
$t-2\geq s\geq 3$
, Conjecture 1.2 is true if
![]() $t>s^2(s-1)/2+s$
,
$t>s^2(s-1)/2+s$
,
![]() $t=s+2$
, or
$t=s+2$
, or
![]() $s=3,4$
.
$s=3,4$
.
Furthermore, our main result shows that a modified version of Conjecture 1.2 is true (which was the motivation for Definition 1.1). It reads as follows.
Theorem 1.4. For all integers
![]() $t-2\geq s\ge 3$
, there is a family of extremal graphs for
$t-2\geq s\ge 3$
, there is a family of extremal graphs for
![]() $\varrho _s(K_t)$
admitting a
$\varrho _s(K_t)$
admitting a
![]() $(b,a)$
-partition for some parameters
$(b,a)$
-partition for some parameters
![]() $1\le a\leq b$
satisfying
$1\le a\leq b$
satisfying
![]() $a+b=t-1$
.
$a+b=t-1$
.
Theorem 1.4 provides a detailed description of the extremal graphs for the generalized Ramsey–Turán problem for cliques, showing that they have simple and bounded structures. We remark that Theorem 1.4 resolves combinatorially the problem of determining the Ramsey–Turán density
![]() $\varrho _s(K_t)$
. Indeed, given s and t, there is a bounded number of choices for a (because
$\varrho _s(K_t)$
. Indeed, given s and t, there is a bounded number of choices for a (because
![]() $a\leq t-1$
). Once a is fixed, the structure of a graph admitting a
$a\leq t-1$
). Once a is fixed, the structure of a graph admitting a
![]() $(b,a)$
-partition is determined, so its
$(b,a)$
-partition is determined, so its
![]() $K_s$
-density may be computed in terms of the fractions of vertices allocated to each part. Thus, Theorem 1.4 reduces determining
$K_s$
-density may be computed in terms of the fractions of vertices allocated to each part. Thus, Theorem 1.4 reduces determining
![]() $\varrho _s(K_t)$
to a bounded optimization problem (over
$\varrho _s(K_t)$
to a bounded optimization problem (over
![]() $a+b=t-1$
).
$a+b=t-1$
).
Organization. The rest of the paper is structured as follows. The proof of Theorem 1.4 consists of two parts. We first reduce it to a more tractable problem about clique densities in weighted graphs (see Theorem 2.4) in Section 2. Understanding this weighted problem is the bulk of the proof (see Theorem 3.1); we study it in Section 3. In Section 4, we give the proof of Theorem 1.3. Concluding remarks are given in Section 5.
Notation. We use
![]() $[n]$
to denote the finite set
$[n]$
to denote the finite set
![]() $\{1,2 ,\ldots ,n\}$
. For a vector
$\{1,2 ,\ldots ,n\}$
. For a vector ![]() , we write
, we write ![]() for its
for its
![]() $\ell _2$
-norm. Let
$\ell _2$
-norm. Let
![]() $G=(V(G), E(G))$
be a graph. For every
$G=(V(G), E(G))$
be a graph. For every
![]() $U,V\subseteq V(G)$
, denote by
$U,V\subseteq V(G)$
, denote by
![]() $G[U,V]$
the induced bipartite subgraph of G on partite sets U and V, and by
$G[U,V]$
the induced bipartite subgraph of G on partite sets U and V, and by
![]() $G[U]$
the induced subgraph of G on set U. For convenience, we let
$G[U]$
the induced subgraph of G on set U. For convenience, we let
![]() $G-U=G[V(G)\setminus U]$
.
$G-U=G[V(G)\setminus U]$
.
2 Reduction to Weighted Graphs
The first step of the proof of Theorem 1.4 reduces understanding Ramsey–Turán density to a problem about clique density in weighted graphs. The aim of this section will be to prove Theorem 2.4, which demonstrates the equivalence between these two problems. However, before we can state Theorem 2.4, we need to define our notion of weighted graphs.
Definition 2.1. A weighted graph
![]() $R=(V,w)$
consists of a finite vertex set V together with a weight function
$R=(V,w)$
consists of a finite vertex set V together with a weight function
![]() $w:V\sqcup V^2\to [0,1]$
satisfying the following two properties. The vertex weights must sum to one (i.e.,
$w:V\sqcup V^2\to [0,1]$
satisfying the following two properties. The vertex weights must sum to one (i.e.,
![]() $\sum _{v\in V}w(v)=1$
). Additionally, the edge weights must satisfy
$\sum _{v\in V}w(v)=1$
). Additionally, the edge weights must satisfy
![]() $w(v,v')=w(v',v)$
and
$w(v,v')=w(v',v)$
and
![]() $w(v,v)=0$
for any
$w(v,v)=0$
for any
![]() $v,v'\in V$
. For
$v,v'\in V$
. For
![]() $\alpha \in [0,1]$
, denote by
$\alpha \in [0,1]$
, denote by
![]() $R_{>\alpha }$
the spanning subgraph of R with all edges of weight larger than
$R_{>\alpha }$
the spanning subgraph of R with all edges of weight larger than
![]() $\alpha $
.
$\alpha $
.
Intuitively, a weighted graph may be thought of as a type of graph limit with a more discrete structure than a graphon. An r-vertex weighted graph can also be considered to represent a large r-partite graph G whose ith part
![]() $V_i$
contains a
$V_i$
contains a
![]() $w(i)$
-fraction of the vertex set, such that each induced bipartite subgraph
$w(i)$
-fraction of the vertex set, such that each induced bipartite subgraph
![]() $G[V_i,V_j]$
is a random graph of density
$G[V_i,V_j]$
is a random graph of density
![]() $w(i,j)$
.
$w(i,j)$
.
With this perspective in mind, we define subgraph densities in a weighted graph.
Definition 2.2. Let H be a graph with vertex set
![]() $[s]$
. The H-density of a weighted graph R is defined as
$[s]$
. The H-density of a weighted graph R is defined as

where vertices
![]() $v_1,\ldots ,v_s\in V(R)$
are chosen independently at random according to the vertex weights of R.
$v_1,\ldots ,v_s\in V(R)$
are chosen independently at random according to the vertex weights of R.
We shall show that the Ramsey–Turán density
![]() $\varrho _{s}(K_t)$
is determined by the maximum possible
$\varrho _{s}(K_t)$
is determined by the maximum possible
![]() $K_s$
-density in a weighted graph avoiding the following forbidden configuration.
$K_s$
-density in a weighted graph avoiding the following forbidden configuration.
Definition 2.3. Let R be a weighted graph and
![]() $t\in \mathbb {N}$
. The weighted t-clique family
$t\in \mathbb {N}$
. The weighted t-clique family
![]() ${ \mathcal {K}}_t$
consists of all pairs of subsets
${ \mathcal {K}}_t$
consists of all pairs of subsets
![]() $(S_1,S_2)$
with
$(S_1,S_2)$
with
![]() $S_2\subseteq S_1\subseteq V(R)$
,
$S_2\subseteq S_1\subseteq V(R)$
,
![]() $s_1=|S_1|,s_2=|S_2|\ge 1$
and
$s_1=|S_1|,s_2=|S_2|\ge 1$
and
![]() $s_1+s_2=t$
such that
$s_1+s_2=t$
such that
![]() $S_1$
induces a
$S_1$
induces a
![]() $K_{s_1}$
in
$K_{s_1}$
in
![]() $R_{>0}$
and
$R_{>0}$
and
![]() $S_2$
induces a
$S_2$
induces a
![]() $K_{s_2}$
in
$K_{s_2}$
in
![]() $R_{>\frac {1}{2}}$
.We say R is
$R_{>\frac {1}{2}}$
.We say R is
![]() ${ \mathcal {K}}_t$
–free if R contains no such pair
${ \mathcal {K}}_t$
–free if R contains no such pair
![]() $(S_1,S_2)$
.
$(S_1,S_2)$
.
We can then define the
![]() $K_s$
-Turán density of
$K_s$
-Turán density of
![]() ${ \mathcal {K}}_t$
as
${ \mathcal {K}}_t$
as
At this point, we may state the main result of this section.
Theorem 2.4. For
![]() $s,t\in \mathbb {N}$
with
$s,t\in \mathbb {N}$
with
![]() $2\leq s\leq t-1$
, we have
$2\leq s\leq t-1$
, we have
![]() $\varrho _{s}(K_t)=\pi _{s}({ \mathcal {K}}_t)$
.
$\varrho _{s}(K_t)=\pi _{s}({ \mathcal {K}}_t)$
.
The upper and lower bounds of Theorem 2.4 will be proven in the next two subsections.
2.1 Upper bound
Our proof of the upper bound on Theorem 2.4 relies on Szemerédi’s regularity lemma. The regularity lemma states that any graph looks
![]() $\varepsilon $
-close to a weighted graph whose number of vertices is bounded in terms of
$\varepsilon $
-close to a weighted graph whose number of vertices is bounded in terms of
![]() $\varepsilon $
. We recall its statement here, beginning with some preliminary definitions.
$\varepsilon $
. We recall its statement here, beginning with some preliminary definitions.
Definition 2.5. Let G be a graph and let
![]() $X, Y\subseteq V(G)$
. The edge density between X and Y, denoted by
$X, Y\subseteq V(G)$
. The edge density between X and Y, denoted by
![]() $d(X,Y)$
, is the fraction of pairs
$d(X,Y)$
, is the fraction of pairs
![]() $(x,y)\in X\times Y$
that are edges of G. Given
$(x,y)\in X\times Y$
that are edges of G. Given
![]() $\varepsilon>0$
, we say the pair
$\varepsilon>0$
, we say the pair
![]() $(X,Y)$
is
$(X,Y)$
is
![]() $\varepsilon $
-regular if, for all
$\varepsilon $
-regular if, for all
![]() $X'\subseteq X$
and
$X'\subseteq X$
and
![]() $Y'\subseteq Y$
with
$Y'\subseteq Y$
with
![]() $|X'|\geq \varepsilon |X|$
and
$|X'|\geq \varepsilon |X|$
and
![]() $|Y'|\geq \varepsilon |Y|$
, we have
$|Y'|\geq \varepsilon |Y|$
, we have
![]() $|d(X',Y')-d(X,Y)|<\varepsilon $
.
$|d(X',Y')-d(X,Y)|<\varepsilon $
.
Definition 2.6. Let G be a graph. A vertex partition
![]() $V(G)=V_1\cup \cdots \cup V_r\cup V_{r+1}$
is called
$V(G)=V_1\cup \cdots \cup V_r\cup V_{r+1}$
is called
![]() $\varepsilon $
-regular if
$\varepsilon $
-regular if
![]() $|V_1|=\cdots =|V_r|$
and
$|V_1|=\cdots =|V_r|$
and
![]() $|V_{r+1}|\leq \varepsilon n$
, and additionally at most
$|V_{r+1}|\leq \varepsilon n$
, and additionally at most
![]() $\varepsilon r^2$
pairs
$\varepsilon r^2$
pairs
![]() $(V_i,V_j)$
with
$(V_i,V_j)$
with
![]() $i<j\leq r$
are not
$i<j\leq r$
are not
![]() $\varepsilon $
-regular.
$\varepsilon $
-regular.
Theorem 2.7 (Regularity Lemma, [Reference Szemerédi36])
For every small constant
![]() $\varepsilon>0$
and integer
$\varepsilon>0$
and integer
![]() $M_0$
, there exists an integer
$M_0$
, there exists an integer
![]() $M=M(\varepsilon ,M_0)$
such that the following holds. Given any n-vertex graph G, there is an
$M=M(\varepsilon ,M_0)$
such that the following holds. Given any n-vertex graph G, there is an
![]() $\varepsilon $
-regular partition of its vertices
$\varepsilon $
-regular partition of its vertices
![]() $V(G)=V_1\cup \cdots \cup V_r\cup V_{r+1}$
such that
$V(G)=V_1\cup \cdots \cup V_r\cup V_{r+1}$
such that
![]() $M_0\leq r\leq M$
.
$M_0\leq r\leq M$
.
We also require the graph counting lemma. Intuitively, if a graph G looks like a weighted graph R, then this lemma implies that the
![]() $K_s$
-density of G is approximately the
$K_s$
-density of G is approximately the
![]() $K_s$
-density of R.
$K_s$
-density of R.
Lemma 2.8 (Graph Counting Lemma, [Reference Duke, Lefmann and Rödl12])
Let
![]() $\varepsilon>0$
, and let G be an s-partite graph with
$\varepsilon>0$
, and let G be an s-partite graph with ![]() . Suppose that the pair
. Suppose that the pair
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\varepsilon $
-regular for all
$\varepsilon $
-regular for all
![]() $1\leq i< j\leq s$
. Then
$1\leq i< j\leq s$
. Then

where
![]() $N(K_s, G)$
is the number of copies of
$N(K_s, G)$
is the number of copies of
![]() $K_s$
in G.
$K_s$
in G.
We now prove the upper bound of Theorem 2.4.
Theorem 2.9. Let
![]() $s,t$
be integers with
$s,t$
be integers with
![]() $2\le s< t$
. For any
$2\le s< t$
. For any
![]() $\delta \in (0,1)$
there exists
$\delta \in (0,1)$
there exists
![]() $\delta '\in (0,1)$
such that the following holds. Suppose G is a
$\delta '\in (0,1)$
such that the following holds. Suppose G is a
![]() $K_t$
-free graph with
$K_t$
-free graph with
![]() $\alpha (G)\leq \delta '|V(G)|$
. Then there is a
$\alpha (G)\leq \delta '|V(G)|$
. Then there is a
![]() ${ \mathcal {K}}_t$
-free weighted graph R such that
${ \mathcal {K}}_t$
-free weighted graph R such that
![]() $d_{K_s}(G)\leq d_{K_s}(R)+4s^2\delta $
.
$d_{K_s}(G)\leq d_{K_s}(R)+4s^2\delta $
.
Proof. Choose
![]() $\varepsilon <\frac 12$
small enough such that
$\varepsilon <\frac 12$
small enough such that
![]() $(\delta -\varepsilon )^{t-1}>(t+1)\varepsilon $
and let
$(\delta -\varepsilon )^{t-1}>(t+1)\varepsilon $
and let
![]() $\delta '=\varepsilon /M$
, where
$\delta '=\varepsilon /M$
, where
![]() $M=M(\varepsilon ,\frac 1\varepsilon )$
is the constant guaranteed by the regularity lemma (Theorem 2.7). Suppose G is a
$M=M(\varepsilon ,\frac 1\varepsilon )$
is the constant guaranteed by the regularity lemma (Theorem 2.7). Suppose G is a
![]() $K_t$
-free graph on N vertices with
$K_t$
-free graph on N vertices with
![]() $\alpha (G)\leq \delta 'N$
.
$\alpha (G)\leq \delta 'N$
.
Apply Theorem 2.7 with this value of
![]() $\varepsilon $
to G. This yields an
$\varepsilon $
to G. This yields an
![]() $\varepsilon $
-regular partition
$\varepsilon $
-regular partition
![]() $V(G)=V_1\cup \cdots \cup V_r\cup V_{r+1}$
with
$V(G)=V_1\cup \cdots \cup V_r\cup V_{r+1}$
with
![]() $\frac 1\varepsilon \leq r\leq M$
. We show that a substructure similar to a weighted t-clique is forbidden among the edge densities
$\frac 1\varepsilon \leq r\leq M$
. We show that a substructure similar to a weighted t-clique is forbidden among the edge densities
![]() $d(V_i,V_j)$
.
$d(V_i,V_j)$
.
Claim 2.10. Suppose
![]() $S_2\subseteq S_1\subseteq [r]$
are sets of indices such that
$S_2\subseteq S_1\subseteq [r]$
are sets of indices such that
-
(i) For any distinct
 $i,j\in S_1$
, the pair
$i,j\in S_1$
, the pair
 $(V_i,V_j)$
is
$(V_i,V_j)$
is
 $\varepsilon $
-regular with density
$\varepsilon $
-regular with density
 $d(V_i,V_j)>\delta $
; and
$d(V_i,V_j)>\delta $
; and -
(ii) For any distinct
 $i,j\in S_2$
, the pair
$i,j\in S_2$
, the pair
 $(V_i,V_j)$
has density
$(V_i,V_j)$
has density
 $d(V_i,V_j)>\frac 12+\delta $
.
$d(V_i,V_j)>\frac 12+\delta $
.
Then G contains a clique of order
![]() $|S_1|+|S_2|$
. In particular,
$|S_1|+|S_2|$
. In particular,
![]() $|S_1|+|S_2|<t$
.
$|S_1|+|S_2|<t$
.
Proof of claim
Order the elements of
![]() $S_1$
as
$S_1$
as
![]() $a_1,\ldots ,a_\ell $
with the elements of
$a_1,\ldots ,a_\ell $
with the elements of
![]() $S_1\setminus S_2$
listed first. Set
$S_1\setminus S_2$
listed first. Set
![]() $k=|S_1|-|S_2|$
. By Lemma 2.8, there exists a clique S of order
$k=|S_1|-|S_2|$
. By Lemma 2.8, there exists a clique S of order
![]() $\ell $
in G such that
$\ell $
in G such that
![]() $|S\cap V_{a_i}|=1$
for each
$|S\cap V_{a_i}|=1$
for each
![]() $i\in [\ell ]$
; as G is
$i\in [\ell ]$
; as G is
![]() $K_t$
-free, it follows that
$K_t$
-free, it follows that
![]() $\ell <t$
. Our proof follows an
$\ell <t$
. Our proof follows an
![]() $\ell $
-step process, where the ith step chooses one (if
$\ell $
-step process, where the ith step chooses one (if
![]() $i\leq k$
) or two (if
$i\leq k$
) or two (if
![]() $i>k$
) vertices from
$i>k$
) vertices from
![]() $V_{a_i}$
that are adjacent to all previously chosen vertices. For
$V_{a_i}$
that are adjacent to all previously chosen vertices. For
![]() $0\leq i,j\leq \ell $
, write
$0\leq i,j\leq \ell $
, write
![]() $W^{(i)}$
for the common neighborhood of those vertices chosen in the first i steps, and let
$W^{(i)}$
for the common neighborhood of those vertices chosen in the first i steps, and let
![]() $W_j^{(i)}=V_{a_j}\cap W^{(i)}$
. In particular,
$W_j^{(i)}=V_{a_j}\cap W^{(i)}$
. In particular,
![]() $W^{(0)}=V(G)$
. We will choose
$W^{(0)}=V(G)$
. We will choose
![]() $2\ell -k$
vertices such that
$2\ell -k$
vertices such that
![]() $|W_j^{(i)}|\geq (\delta -\varepsilon )|W_j^{(i-1)}|\geq (\delta -\varepsilon )^i|V_{a_j}|$
for all
$|W_j^{(i)}|\geq (\delta -\varepsilon )|W_j^{(i-1)}|\geq (\delta -\varepsilon )^i|V_{a_j}|$
for all
![]() $0\leq i<j\leq \ell $
.
$0\leq i<j\leq \ell $
.
On the ith step with
![]() $1\leq i\leq k$
, choose one vertex
$1\leq i\leq k$
, choose one vertex
![]() $v_i\in W_i^{(i-1)}$
such that
$v_i\in W_i^{(i-1)}$
such that
![]() $W_j^{(i)}:=N(v_i)\cap W_j^{(i-1)}$
has cardinality at least
$W_j^{(i)}:=N(v_i)\cap W_j^{(i-1)}$
has cardinality at least
![]() $(\delta -\varepsilon )|W_j^{(i-1)}|$
for each
$(\delta -\varepsilon )|W_j^{(i-1)}|$
for each
![]() $j>i$
. To show that such a vertex
$j>i$
. To show that such a vertex
![]() $v_i$
exists, consider the sets
$v_i$
exists, consider the sets
for each
![]() $j>i$
. Observe that
$j>i$
. Observe that
![]() $d\left (X_j,W_j^{(i-1)}\right )<\delta -\varepsilon <d(V_{a_i},V_{a_j})-\varepsilon $
by construction, and that
$d\left (X_j,W_j^{(i-1)}\right )<\delta -\varepsilon <d(V_{a_i},V_{a_j})-\varepsilon $
by construction, and that
![]() $|W_j^{(i-1)}|\geq (\delta -\varepsilon )^{i-1}|V_{a_j}|\geq (\delta -\varepsilon )^t|V_{a_j}|\geq \varepsilon |V_{a_j}|$
. Because the pair
$|W_j^{(i-1)}|\geq (\delta -\varepsilon )^{i-1}|V_{a_j}|\geq (\delta -\varepsilon )^t|V_{a_j}|\geq \varepsilon |V_{a_j}|$
. Because the pair
![]() $(V_{a_i},V_{a_j})$
is
$(V_{a_i},V_{a_j})$
is
![]() $\varepsilon $
-regular, it follows that
$\varepsilon $
-regular, it follows that
![]() $|X_j|<\varepsilon |V_{a_i}|$
. Thus,
$|X_j|<\varepsilon |V_{a_i}|$
. Thus,

It follows that there is a vertex
![]() $v_i\in W_i^{(i-1)}$
such that
$v_i\in W_i^{(i-1)}$
such that
![]() $|W_j^{(i)}|=|N(v_i)\cap W_j^{(i-1)}|\geq (\delta -\varepsilon )|W_j^{(i-1)}|$
for each
$|W_j^{(i)}|=|N(v_i)\cap W_j^{(i-1)}|\geq (\delta -\varepsilon )|W_j^{(i-1)}|$
for each
![]() $j>i$
.
$j>i$
.
On the ith step with
![]() $k<i\leq \ell $
, choose two adjacent vertices
$k<i\leq \ell $
, choose two adjacent vertices
![]() $v_i,v^{\prime }_i\in W_i^{(i-1)}$
such that
$v_i,v^{\prime }_i\in W_i^{(i-1)}$
such that
![]() $W_j^{(i)}:=N(v_i)\cap N(v^{\prime }_i)\cap W_j^{(i-1)}$
has cardinality at least
$W_j^{(i)}:=N(v_i)\cap N(v^{\prime }_i)\cap W_j^{(i-1)}$
has cardinality at least
![]() $2(\delta -\varepsilon )|W_j^{(i-1)}|$
for all
$2(\delta -\varepsilon )|W_j^{(i-1)}|$
for all
![]() $j>i$
. To verify that such vertices exist, set
$j>i$
. To verify that such vertices exist, set

for each
![]() $j>i$
. The argument from the prior paragraph shows that
$j>i$
. The argument from the prior paragraph shows that

Noting that
![]() $|V_{a_i}|=(N-|V_{r+1}|)/r>N/2r$
, we have
$|V_{a_i}|=(N-|V_{r+1}|)/r>N/2r$
, we have

It follows that there are adjacent vertices
![]() $v_i,v^{\prime }_i\in W_i^{(i-1)}$
such that
$v_i,v^{\prime }_i\in W_i^{(i-1)}$
such that
![]() $N(v_i)\cap W_j^{(i-1)}$
and
$N(v_i)\cap W_j^{(i-1)}$
and
![]() $N(v^{\prime }_i)\cap W_j^{(i-1)}$
have cardinality at least
$N(v^{\prime }_i)\cap W_j^{(i-1)}$
have cardinality at least
![]() $(1/2+\delta -\varepsilon )|W_j^{(i-1)}|$
for each
$(1/2+\delta -\varepsilon )|W_j^{(i-1)}|$
for each
![]() $j>i$
. By the pigeonhole principle,
$j>i$
. By the pigeonhole principle,
for each
![]() $j>i$
, as desired.
$j>i$
, as desired.
After
![]() $\ell $
steps, this process results in
$\ell $
steps, this process results in
![]() $k+2(\ell -k)=|S_1|+|S_2|$
vertices
$k+2(\ell -k)=|S_1|+|S_2|$
vertices
![]() $v_1,\ldots ,v_k,v_{k+1},v^{\prime }_{k+1},\ldots ,v_\ell ,v^{\prime }_\ell $
that form a clique in G. It follows that
$v_1,\ldots ,v_k,v_{k+1},v^{\prime }_{k+1},\ldots ,v_\ell ,v^{\prime }_\ell $
that form a clique in G. It follows that
![]() $|S_1|+|S_2|<t$
, because G is
$|S_1|+|S_2|<t$
, because G is
![]() $K_t$
-free.
$K_t$
-free.
Let R be the weighted graph on
![]() $[r]$
with vertex weights
$[r]$
with vertex weights
![]() $w(i)=\frac 1r$
for all
$w(i)=\frac 1r$
for all
![]() $i\in [r]$
and edge weights
$i\in [r]$
and edge weights

for all
![]() $i,j\in [r]$
. We observe that R is
$i,j\in [r]$
. We observe that R is
![]() ${ \mathcal {K}}_t$
-free as a direct consequence of Claim 2.10.
${ \mathcal {K}}_t$
-free as a direct consequence of Claim 2.10.
To conclude the proof, we bound the
![]() $K_s$
-density of G. We have
$K_s$
-density of G. We have

If
![]() $a_1,\ldots ,a_s$
are distinct elements of
$a_1,\ldots ,a_s$
are distinct elements of
![]() $[r]$
and each pair
$[r]$
and each pair
![]() $(V_{a_i},V_{a_j})$
is
$(V_{a_i},V_{a_j})$
is
![]() $\varepsilon $
-regular, then we may simplify the summand using the graph-counting lemma. Indeed, Lemma 2.8 implies that the number of copies of
$\varepsilon $
-regular, then we may simplify the summand using the graph-counting lemma. Indeed, Lemma 2.8 implies that the number of copies of
![]() $K_s$
in
$K_s$
in
![]() $V_{a_1}\times \cdots \times V_{a_s}$
is at most
$V_{a_1}\times \cdots \times V_{a_s}$
is at most

in this case. It remains to bound the contribution from terms where some
![]() $a_i$
is
$a_i$
is
![]() $r+1$
, the
$r+1$
, the
![]() $a_i$
are not distinct, or some pair
$a_i$
are not distinct, or some pair
![]() $(V_{a_i},V_{a_j})$
is not
$(V_{a_i},V_{a_j})$
is not
![]() $\varepsilon $
-regular.
$\varepsilon $
-regular.
The terms where at least one index
![]() $a_i$
equals
$a_i$
equals
![]() $r+1$
contribute at most
$r+1$
contribute at most
to the sum. The terms where
![]() $a_1,\ldots ,a_s$
are not all distinct contribute at most
$a_1,\ldots ,a_s$
are not all distinct contribute at most

because
![]() $r\geq 1/\varepsilon $
. The terms where a pair
$r\geq 1/\varepsilon $
. The terms where a pair
![]() $(V_{a_i},V_{a_j})$
is not
$(V_{a_i},V_{a_j})$
is not
![]() $\varepsilon $
-regular contribute at most
$\varepsilon $
-regular contribute at most

Combining these estimates, we have

To compare this to
![]() $d_{K_s}(R)$
, we observe the following inequality. If real numbers
$d_{K_s}(R)$
, we observe the following inequality. If real numbers
![]() $x_1,\ldots ,x_k,y_1,\ldots ,y_k\in [0,1]$
satisfy
$x_1,\ldots ,x_k,y_1,\ldots ,y_k\in [0,1]$
satisfy
![]() $x_i\leq y_i+\delta $
for each
$x_i\leq y_i+\delta $
for each
![]() $i\in [k]$
then
$i\in [k]$
then

Applying this inequality with ![]() to the real numbers
to the real numbers
![]() $d(V_{a_i},V_{a_j})$
and
$d(V_{a_i},V_{a_j})$
and
![]() $w(a_i,a_j)$
, it follows that
$w(a_i,a_j)$
, it follows that

Because
![]() $\varepsilon <(\delta -\varepsilon )^{t-1}<\delta ^2$
, it follows that
$\varepsilon <(\delta -\varepsilon )^{t-1}<\delta ^2$
, it follows that
![]() $d_{K_s}(G)<d_{K_s}(R)+4s^2\delta $
, as desired.
$d_{K_s}(G)<d_{K_s}(R)+4s^2\delta $
, as desired.
2.2 Lower bound
The lower bound construction for Theorem 2.4 hinges on a construction of Bollobás and Erdős [Reference Bollobás and Erdős10] which achieves the tight lower bound
![]() $\varrho _2(K_4)=\frac {1}{4}$
. We briefly describe this construction, following the notation used in [Reference Fox, Loh and Zhao18].
$\varrho _2(K_4)=\frac {1}{4}$
. We briefly describe this construction, following the notation used in [Reference Fox, Loh and Zhao18].
Fix
![]() $0<\varepsilon <1$
and an integer
$0<\varepsilon <1$
and an integer
![]() $h\geq 16$
, and set
$h\geq 16$
, and set
![]() $\mu =\frac {\varepsilon }{\sqrt h}$
. Let X and Y be sets of points on the unit sphere
$\mu =\frac {\varepsilon }{\sqrt h}$
. Let X and Y be sets of points on the unit sphere
![]() $\textsf {S}^{h-1}\subset \mathbb R^h$
. The Bollobás–Erdős graph
$\textsf {S}^{h-1}\subset \mathbb R^h$
. The Bollobás–Erdős graph
![]() $\mathrm {BE}(X,Y)$
is a graph on vertex set
$\mathrm {BE}(X,Y)$
is a graph on vertex set
![]() $X\cup Y$
constructed as follows.
$X\cup Y$
constructed as follows.
-
(a) Join
 to
to  if
if  .
. -
(b) Join
 if
if  . Similarly, join
. Similarly, join  if
if  .
.
Bollobás and Erdős showed that this graph is
![]() $K_4$
-free and that, if
$K_4$
-free and that, if
![]() $\varepsilon $
and h are tuned appropriately and X and Y are uniformly placed on
$\varepsilon $
and h are tuned appropriately and X and Y are uniformly placed on
![]() $\textsf {S}^{h-1}$
, it has independence number
$\textsf {S}^{h-1}$
, it has independence number
![]() $o(|X|+|Y|)$
and edge density
$o(|X|+|Y|)$
and edge density
![]() $\frac 14-o(1)$
. Fox, Loh and Zhao [Reference Fox, Loh and Zhao18] analyzed this construction in further detail, providing precise quantitative results on the independence number and minimum degree. We need some results from their work.
$\frac 14-o(1)$
. Fox, Loh and Zhao [Reference Fox, Loh and Zhao18] analyzed this construction in further detail, providing precise quantitative results on the independence number and minimum degree. We need some results from their work.
Lemma 2.11 [Reference Fox, Loh and Zhao18]
Let
![]() $0<\varepsilon <1$
and let
$0<\varepsilon <1$
and let
![]() $h\geq 16$
be an integer. Set
$h\geq 16$
be an integer. Set
![]() $\mu =\varepsilon /\sqrt h$
.
$\mu =\varepsilon /\sqrt h$
.
-
(1) If points
 are chosen independently and uniformly at random then
are chosen independently and uniformly at random then  .
.
Now, fix
![]() $X,Y\subseteq \textsf {S}^{h-1}$
, and let
$X,Y\subseteq \textsf {S}^{h-1}$
, and let
![]() $G=\mathrm {BE}(X,Y)$
be the graph defined above with parameters
$G=\mathrm {BE}(X,Y)$
be the graph defined above with parameters
![]() $\varepsilon $
and h.
$\varepsilon $
and h.
-
(2) The induced subgraphs
 $G[X]$
and
$G[X]$
and
 $G[Y]$
are each
$G[Y]$
are each
 $K_3$
-free.
$K_3$
-free. -
(3) G is
 $K_4$
-free.
$K_4$
-free. -
(4) If n is sufficiently large in terms of
 $\varepsilon , h$
, there is a choice
$\varepsilon , h$
, there is a choice
 $X\subset \textsf {S}^h$
of size n such that the induced subgraph
$X\subset \textsf {S}^h$
of size n such that the induced subgraph
 $G[X]$
has independence number at most
$G[X]$
has independence number at most
 $e^{-\varepsilon \sqrt h/4}n$
.
$e^{-\varepsilon \sqrt h/4}n$
.
Using these preliminaries, we prove the lower bound of Theorem 2.4. It follows from Theorem 2.12 by choosing parameters
![]() $(\varepsilon ,h)$
such that
$(\varepsilon ,h)$
such that
![]() $\varepsilon \to 0$
and
$\varepsilon \to 0$
and
![]() $\varepsilon \sqrt h\to \infty $
.
$\varepsilon \sqrt h\to \infty $
.
Theorem 2.12. Suppose R is a weighted graph that is
![]() ${ \mathcal {K}}_t$
-free for some integer
${ \mathcal {K}}_t$
-free for some integer
![]() $t\geq 3$
. Fix
$t\geq 3$
. Fix
![]() $\varepsilon>0$
and an integer
$\varepsilon>0$
and an integer
![]() $h\geq 16$
. For all sufficiently large N, there is a
$h\geq 16$
. For all sufficiently large N, there is a
![]() $K_t$
-free graph G on N vertices with independence number
$K_t$
-free graph G on N vertices with independence number
![]() $\alpha (G)\leq 3e^{-\varepsilon \sqrt h/4}N$
and
$\alpha (G)\leq 3e^{-\varepsilon \sqrt h/4}N$
and
![]() $K_s$
-density
$K_s$
-density
![]() $d_{K_s}(G)\geq (1-2\sqrt 2s^2\varepsilon )d_{K_s}(R)$
.
$d_{K_s}(G)\geq (1-2\sqrt 2s^2\varepsilon )d_{K_s}(R)$
.
Proof. Suppose that
![]() $V(R)=[r]$
for some integer r. Increasing each edge weight to the next multiple of
$V(R)=[r]$
for some integer r. Increasing each edge weight to the next multiple of
![]() $\frac 12$
preserves the
$\frac 12$
preserves the
![]() ${ \mathcal {K}}_t$
-freeness of R, so we may assume that all edge weights of R are 0,
${ \mathcal {K}}_t$
-freeness of R, so we may assume that all edge weights of R are 0,
![]() $\frac 12$
, or
$\frac 12$
, or
![]() $1$
. Set
$1$
. Set
![]() $\mu =\frac {\varepsilon }{\sqrt h}$
as in the Bollobás–Erdős construction.
$\mu =\frac {\varepsilon }{\sqrt h}$
as in the Bollobás–Erdős construction.
Choose integers
![]() $n_i\geq \lfloor w(i)N\rfloor $
such that
$n_i\geq \lfloor w(i)N\rfloor $
such that
![]() $N=n_1+\cdots +n_r$
. We construct an N-vertex graph G on vertex set
$N=n_1+\cdots +n_r$
. We construct an N-vertex graph G on vertex set
![]() $V_1\cup \cdots \cup V_r$
as follows. Intuitively,
$V_1\cup \cdots \cup V_r$
as follows. Intuitively,
![]() $G[V_i,V_j]$
will be complete, empty, or a randomly rotated Bollobás–Erdős graph, depending on whether
$G[V_i,V_j]$
will be complete, empty, or a randomly rotated Bollobás–Erdős graph, depending on whether
![]() $w(i,j)$
is 1, 0, or
$w(i,j)$
is 1, 0, or
![]() $\frac 12$
.
$\frac 12$
.
Suppose N is sufficiently large. For each i, we may choose a set
![]() $V_i$
of
$V_i$
of
![]() $n_i$
points on
$n_i$
points on
![]() $\textsf {S}^{h-1}$
satisfying Lemma 2.11(4). Connect vertices in
$\textsf {S}^{h-1}$
satisfying Lemma 2.11(4). Connect vertices in ![]() as follows. Within each part
as follows. Within each part
![]() $V_i$
, add an edge between
$V_i$
, add an edge between ![]() if
if ![]() . Let
. Let
![]() $G[V_i,V_j]$
be complete bipartite if
$G[V_i,V_j]$
be complete bipartite if
![]() $w(i,j)=1$
and empty if
$w(i,j)=1$
and empty if
![]() $w(i,j)=0$
. If
$w(i,j)=0$
. If
![]() $w(i,j)=\frac 12$
for some
$w(i,j)=\frac 12$
for some
![]() $i<j$
, then let
$i<j$
, then let
![]() $\rho _{ij}\in SO(h)$
be a rotation of
$\rho _{ij}\in SO(h)$
be a rotation of
![]() $\textsf {S}^{h-1}$
chosen uniformly at random. Connect
$\textsf {S}^{h-1}$
chosen uniformly at random. Connect ![]() and
and ![]() if
if ![]() .
.
Observe that each induced subgraph
![]() $G[V_i]$
is
$G[V_i]$
is
![]() $K_3$
-free with independence number
$K_3$
-free with independence number
![]() $\alpha (G[V_i])\leq e^{-\varepsilon \sqrt h/4}n_i$
by Lemma 2.11(2) and (4). It follows that
$\alpha (G[V_i])\leq e^{-\varepsilon \sqrt h/4}n_i$
by Lemma 2.11(2) and (4). It follows that
![]() $\alpha (G)\leq e^{-\varepsilon \sqrt h/4}N$
. Additionally, if
$\alpha (G)\leq e^{-\varepsilon \sqrt h/4}N$
. Additionally, if
![]() $w(i,j)=\frac 12$
, the induced subgraph
$w(i,j)=\frac 12$
, the induced subgraph
![]() $G[V_i\cup V_j]$
is the Bollobás–Erdős graph
$G[V_i\cup V_j]$
is the Bollobás–Erdős graph
![]() $\mathrm {BE}(\rho _{ij}(V_i),V_j)$
, and is thus
$\mathrm {BE}(\rho _{ij}(V_i),V_j)$
, and is thus
![]() $K_4$
-free by Lemma 2.11(3).
$K_4$
-free by Lemma 2.11(3).
Using these properties, we verify that G is
![]() $K_t$
-free. Suppose, for contradiction, that
$K_t$
-free. Suppose, for contradiction, that
![]() $G[W]$
is a clique, where W is some set of t vertices. Let
$G[W]$
is a clique, where W is some set of t vertices. Let
![]() $S_1{\kern-1pt}={\kern-1pt}\{i\in [r]{\kern-1pt}:{\kern-1pt}|V_i{\kern-1pt}\cap{\kern-1pt} W|{\kern-1pt}\geq{\kern-1pt} 1\}$
and
$S_1{\kern-1pt}={\kern-1pt}\{i\in [r]{\kern-1pt}:{\kern-1pt}|V_i{\kern-1pt}\cap{\kern-1pt} W|{\kern-1pt}\geq{\kern-1pt} 1\}$
and
![]() $S_2{\kern-1pt}={\kern-1pt}\{i{\kern-1pt}\in{\kern-1pt} [r]{\kern-1pt}:{\kern-1pt}|V_i{\kern-1pt}\cap{\kern-1pt} W|{\kern-1pt}\geq{\kern-1pt} 2\}\subseteq S_1$
. Because each induced subgraph
$S_2{\kern-1pt}={\kern-1pt}\{i{\kern-1pt}\in{\kern-1pt} [r]{\kern-1pt}:{\kern-1pt}|V_i{\kern-1pt}\cap{\kern-1pt} W|{\kern-1pt}\geq{\kern-1pt} 2\}\subseteq S_1$
. Because each induced subgraph
![]() $G[V_i]$
is
$G[V_i]$
is
![]() $K_3$
-free, it follows that W has at most two points in
$K_3$
-free, it follows that W has at most two points in
![]() $V_i$
, and thus that
$V_i$
, and thus that
![]() $|S_1|+|S_2|=|W|=t$
. For any distinct
$|S_1|+|S_2|=|W|=t$
. For any distinct
![]() $i,j\in S_1$
, there is an edge between
$i,j\in S_1$
, there is an edge between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
, and it follows that
$V_j$
, and it follows that
![]() $w(i,j)>0$
. Additionally, for any distinct
$w(i,j)>0$
. Additionally, for any distinct
![]() $i,j\in S_2$
, there is a
$i,j\in S_2$
, there is a
![]() $K_4$
in
$K_4$
in
![]() $G[V_i\cup V_j]$
. Because the Bollobás–Erdős graph is
$G[V_i\cup V_j]$
. Because the Bollobás–Erdős graph is
![]() $K_4$
-free, this implies that
$K_4$
-free, this implies that
![]() $w(i,j)>\frac 12$
. We conclude that
$w(i,j)>\frac 12$
. We conclude that
![]() $(S_1,S_2)$
form a weighted t-clique in R, which is a contradiction. It follows that G is
$(S_1,S_2)$
form a weighted t-clique in R, which is a contradiction. It follows that G is
![]() $K_t$
-free.
$K_t$
-free.
Lastly, we verify that G has large
![]() $K_s$
-density in expectation, using the independence of the random rotations
$K_s$
-density in expectation, using the independence of the random rotations
![]() $\rho _{ij}$
. By Lemma 2.11(1), if
$\rho _{ij}$
. By Lemma 2.11(1), if
![]() $w(i,j)=\frac 12$
then the expected edge density between
$w(i,j)=\frac 12$
then the expected edge density between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
is at least
$V_j$
is at least
![]() $\frac 12-2\sqrt 2\varepsilon $
. Thus, if N is sufficiently large, we have
$\frac 12-2\sqrt 2\varepsilon $
. Thus, if N is sufficiently large, we have

We conclude that there is a choice of the rotations
![]() $\rho _{ij}$
such that
$\rho _{ij}$
such that
![]() $d_{K_s}(G)\geq (1-2\sqrt 2 s^2\varepsilon )d_{K_s}(R)$
.
$d_{K_s}(G)\geq (1-2\sqrt 2 s^2\varepsilon )d_{K_s}(R)$
.
3 Understanding the extremal weighted graphs
By Theorem 2.4,
![]() $\varrho _{s}(K_t)=\pi _{s}({ \mathcal {K}}_t)$
for all
$\varrho _{s}(K_t)=\pi _{s}({ \mathcal {K}}_t)$
for all
![]() $3\leq s\leq t-2$
. In this section, we show that the supremum
$3\leq s\leq t-2$
. In this section, we show that the supremum
![]() $\pi _{s}({ \mathcal {K}}_t)$
is attained by a weighted graph on at most
$\pi _{s}({ \mathcal {K}}_t)$
is attained by a weighted graph on at most
![]() $t-1$
vertices, and characterize the structure of a minimum-size extremal weighted graph more precisely. Our results are summarized as follows; together with Theorem 2.4, they imply Theorem 1.4.
$t-1$
vertices, and characterize the structure of a minimum-size extremal weighted graph more precisely. Our results are summarized as follows; together with Theorem 2.4, they imply Theorem 1.4.
Theorem 3.1. Fix integers
![]() $s,t$
satisfying
$s,t$
satisfying
![]() $3\leq s\leq t-2$
. There is an extremal
$3\leq s\leq t-2$
. There is an extremal
![]() ${ \mathcal {K}}_t$
-free weighted graph R achieving
${ \mathcal {K}}_t$
-free weighted graph R achieving
![]() $K_s$
-density
$K_s$
-density
![]() $\pi _{s}({ \mathcal {K}}_t)$
and satisfying the following properties.
$\pi _{s}({ \mathcal {K}}_t)$
and satisfying the following properties.
-
(A1) For any distinct
 $v,v'\in V(R)$
, we have
$v,v'\in V(R)$
, we have
 $w(v,v')\in \{\frac 12,1\}$
.
$w(v,v')\in \{\frac 12,1\}$
. -
(A2) There is a partition
 $V(R)=B_1\cup \cdots \cup B_a$
into nonempty parts such that vertices inside the same part
$V(R)=B_1\cup \cdots \cup B_a$
into nonempty parts such that vertices inside the same part
 $B_i$
have the same weight, and an edge has weight
$B_i$
have the same weight, and an edge has weight
 $1/2$
if it lies within some
$1/2$
if it lies within some
 $B_i$
and weight 1 otherwise. Moreover, setting
$B_i$
and weight 1 otherwise. Moreover, setting
 $b=\sum _{i\in [a]}|B_i|=|V(R)|$
, we have
$b=\sum _{i\in [a]}|B_i|=|V(R)|$
, we have
 $b\geq s$
and
$b\geq s$
and
 $a+b= t-1$
.
$a+b= t-1$
. -
(A3) For any i and j, the cardinalities
 $|B_i|$
and
$|B_i|$
and
 $|B_j|$
differ by at most 1.
$|B_j|$
differ by at most 1. -
(A4) If
 $|B_i|\geq |B_j|$
for any (possibly equal)
$|B_i|\geq |B_j|$
for any (possibly equal)
 $i,j\in [a]$
, then
$i,j\in [a]$
, then
 $w(v_i)\leq w(v_j)$
for any
$w(v_i)\leq w(v_j)$
for any
 $v_i\in B_i$
and
$v_i\in B_i$
and
 $v_j\in B_j$
. In particular, if
$v_j\in B_j$
. In particular, if
 $|B_i|=|B_j|$
then all vertices in
$|B_i|=|B_j|$
then all vertices in
 $B_i$
and
$B_i$
and
 $B_j$
have the same weight.
$B_j$
have the same weight. -
(A5) Either
 $a=1$
and
$a=1$
and
 $|B_1|=s$
or
$|B_1|=s$
or
 $a\geq 2$
and
$a\geq 2$
and
 $|B_i| \le s-1$
for each
$|B_i| \le s-1$
for each
 $i\in [a]$
.
$i\in [a]$
.
Moreover, all extremal
![]() ${ \mathcal {K}}_t$
-free weighted graphs with minimum order satisfy (A1)–(A5).
${ \mathcal {K}}_t$
-free weighted graphs with minimum order satisfy (A1)–(A5).
Let t and s be integers such that
![]() $3\leq s\leq t-2$
. We shall show in the following subsections that there exists a
$3\leq s\leq t-2$
. We shall show in the following subsections that there exists a
![]() ${ \mathcal {K}}_t$
-free weighted graph R achieving
${ \mathcal {K}}_t$
-free weighted graph R achieving
![]() $K_s$
-density
$K_s$
-density
![]() $\pi _{s}({ \mathcal {K}}_t)$
with
$\pi _{s}({ \mathcal {K}}_t)$
with
![]() $|V(R)|$
minimized and satisfying (A1)–(A5). Note that the weighted graph R might not be unique.
$|V(R)|$
minimized and satisfying (A1)–(A5). Note that the weighted graph R might not be unique.
Before beginning the proof, we introduce some notation which will be used in this section. Let R be a weighted graph and let H be a graph on
![]() $[s]$
. For a vertex set
$[s]$
. For a vertex set
![]() $S\subseteq V(R)$
, the density of copies of H containing S is denoted by
$S\subseteq V(R)$
, the density of copies of H containing S is denoted by

Similarly, write

for the density of copies of H within S and avoiding S, respectively. For convenience, we write
![]() $d_H(R,v)$
instead of
$d_H(R,v)$
instead of
![]() $d_H(R,\{v\})$
and
$d_H(R,\{v\})$
and
![]() $d_H(R-v)$
instead of
$d_H(R-v)$
instead of
![]() $d_H(R-\{v\})$
. Additionally, when
$d_H(R-\{v\})$
. Additionally, when
![]() $H=K_0$
, we define all densities to be 1.
$H=K_0$
, we define all densities to be 1.
We shall also require the following well-known inequality regarding symmetric functions. This is a special case of Maclaurin’s inequality.
Lemma 3.2. Let
![]() $x_1,\ldots ,x_n$
be positive real numbers and let
$x_1,\ldots ,x_n$
be positive real numbers and let
![]() $x=(x_1+\cdots +x_n)/n$
be their average. For any integer
$x=(x_1+\cdots +x_n)/n$
be their average. For any integer
![]() $1\leq k\leq n$
, we have
$1\leq k\leq n$
, we have

with equality if and only if all the
![]() $x_i$
are equal.
$x_i$
are equal.
3.1 Proof of (A1)
For each integer
![]() $n\geq s$
, let
$n\geq s$
, let
![]() $R_n$
be an n-vertex
$R_n$
be an n-vertex
![]() ${ \mathcal {K}}_t$
-free weighted graph of maximum
${ \mathcal {K}}_t$
-free weighted graph of maximum
![]() $K_s$
-density. Such a weighted graph
$K_s$
-density. Such a weighted graph
![]() $R_n$
exists because the space of n-vertex weighted graphs, which is parametrized by possible choices of the vertex and edge weights, is compact.
$R_n$
exists because the space of n-vertex weighted graphs, which is parametrized by possible choices of the vertex and edge weights, is compact.
We claim that
![]() $d_{K_s}(R_{n-1})\geq d_{K_s}(R_n)$
if
$d_{K_s}(R_{n-1})\geq d_{K_s}(R_n)$
if
![]() $R_n$
contains an edge of weight 0. Suppose that
$R_n$
contains an edge of weight 0. Suppose that
![]() $w(v_1,v_2) = 0$
for two distinct vertices
$w(v_1,v_2) = 0$
for two distinct vertices
![]() $v_1,v_2\in V(R_n)$
. For
$v_1,v_2\in V(R_n)$
. For
![]() $i\in [2]$
, let
$i\in [2]$
, let
![]() $R^{\prime }_i$
be the
$R^{\prime }_i$
be the
![]() $(n-1)$
-vertex weighted graph obtained from
$(n-1)$
-vertex weighted graph obtained from
![]() $R_n$
by deleting
$R_n$
by deleting
![]() $v_{3-i}$
and increasing the weight of
$v_{3-i}$
and increasing the weight of
![]() $v_i$
to
$v_i$
to
![]() $w(v_1)+w(v_2)$
. Clearly, both
$w(v_1)+w(v_2)$
. Clearly, both
![]() $R^{\prime }_1$
and
$R^{\prime }_1$
and
![]() $R^{\prime }_2$
are
$R^{\prime }_2$
are
![]() ${ \mathcal {K}}_t$
-free. Moreover, writing
${ \mathcal {K}}_t$
-free. Moreover, writing
![]() $\alpha _i= \frac {w(v_i)}{w(v_1)+w(v_2)}$
for
$\alpha _i= \frac {w(v_i)}{w(v_1)+w(v_2)}$
for
![]() $i\in [2]$
, we have
$i\in [2]$
, we have

This implies
![]() $d_{K_s}(R_{n-1})\geq \max _{i\in [2]}d_{K_s}(R^{\prime }_i)\geq d_{K_s}(R_n)$
. In particular, we have
$d_{K_s}(R_{n-1})\geq \max _{i\in [2]}d_{K_s}(R^{\prime }_i)\geq d_{K_s}(R_n)$
. In particular, we have
![]() $d_{K_s}(R_{n-1})\geq d_{K_s}(R_n)$
for all
$d_{K_s}(R_{n-1})\geq d_{K_s}(R_n)$
for all
![]() $n\geq t$
, as any
$n\geq t$
, as any
![]() ${ \mathcal {K}}_t$
-free weighted graph on at least t vertices must contain an edge of weight 0.
${ \mathcal {K}}_t$
-free weighted graph on at least t vertices must contain an edge of weight 0.
It follows that
![]() $\pi _s({ \mathcal {K}}_t)=\sup _{n\geq s}d_{K_s}(R_n)$
is attained by a weighted graph
$\pi _s({ \mathcal {K}}_t)=\sup _{n\geq s}d_{K_s}(R_n)$
is attained by a weighted graph
![]() $R_n$
on at most
$R_n$
on at most
![]() $t-1$
vertices. Moreover, any minimal-order weighted graph attaining the
$t-1$
vertices. Moreover, any minimal-order weighted graph attaining the
![]() $K_s$
-density
$K_s$
-density
![]() $\pi _s({ \mathcal {K}}_t)$
must have strictly positive edge weights.
$\pi _s({ \mathcal {K}}_t)$
must have strictly positive edge weights.
We conclude the proof of (A1) by observing that if R is a
![]() ${ \mathcal {K}}_t$
-free weighted graph with maximum
${ \mathcal {K}}_t$
-free weighted graph with maximum
![]() $K_s$
-density and strictly positive edge weights, then all edge weights of R must be either
$K_s$
-density and strictly positive edge weights, then all edge weights of R must be either
![]() $\frac 12$
or 1, as increasing any edge weight to the next multiple of
$\frac 12$
or 1, as increasing any edge weight to the next multiple of
![]() $\frac 12$
will preserve the
$\frac 12$
will preserve the
![]() ${ \mathcal {K}}_t$
-freeness of R while increasing its
${ \mathcal {K}}_t$
-freeness of R while increasing its
![]() $K_s$
-density.
$K_s$
-density.
In the remaining subsections, we will show that any extremal
![]() $\mathcal K_t$
-free weighted graph satisfying (A1) — and in particular, all such graphs of minimum order — also satisfy (A2)–(A5).
$\mathcal K_t$
-free weighted graph satisfying (A1) — and in particular, all such graphs of minimum order — also satisfy (A2)–(A5).
3.2 Proof of (A2)
Let R be an extremal
![]() $\mathcal K_t$
-free weighted graph satisfying (A1). We observe that R must have at least s vertices, as
$\mathcal K_t$
-free weighted graph satisfying (A1). We observe that R must have at least s vertices, as
![]() $d_{K_s}(R)$
would be 0 if
$d_{K_s}(R)$
would be 0 if
![]() $|V(R)|<s$
. Moreover, if R has exactly s vertices, say
$|V(R)|<s$
. Moreover, if R has exactly s vertices, say
![]() $v_1,\ldots ,v_s$
, then
$v_1,\ldots ,v_s$
, then

is maximized when the vertex weights are equal and the number of edges of weight 1 is maximized subject to the constraint that
![]() $R_{>1/2}$
is
$R_{>1/2}$
is
![]() $K_{t-s}$
-free. The latter condition holds if and only if
$K_{t-s}$
-free. The latter condition holds if and only if
![]() $R_{>1/2}$
, viewed as an unweighted graph, is the Turán graph
$R_{>1/2}$
, viewed as an unweighted graph, is the Turán graph
![]() $T_{t-s-1}(s)$
. Equivalently,
$T_{t-s-1}(s)$
. Equivalently,
![]() $V(R)$
must admit a partition
$V(R)$
must admit a partition
![]() $V(R)=B_1\cup \cdots \cup B_a$
with
$V(R)=B_1\cup \cdots \cup B_a$
with
![]() $a\leq t-s-1$
such that edges have weight
$a\leq t-s-1$
such that edges have weight
![]() $1/2$
if they lie within some part
$1/2$
if they lie within some part
![]() $B_i$
and weight 1 otherwise.
$B_i$
and weight 1 otherwise.
We now show that R admits such a partition if
![]() $|V(R)|=b\geq s+1$
. It suffices to show that any two vertices
$|V(R)|=b\geq s+1$
. It suffices to show that any two vertices
![]() $v_1,v_2\in V(R)$
with
$v_1,v_2\in V(R)$
with
![]() $w(v_1,v_2)=\frac {1}{2}$
must be identical [i.e.,
$w(v_1,v_2)=\frac {1}{2}$
must be identical [i.e.,
![]() $w(v_1)=w(v_2)$
and
$w(v_1)=w(v_2)$
and
![]() $e(v_1,u)=e(v_2,u)$
for any third vertex
$e(v_1,u)=e(v_2,u)$
for any third vertex
![]() $u\in V(R)$
]. For
$u\in V(R)$
]. For
![]() $i\in [2]$
, let
$i\in [2]$
, let
![]() $R_i$
be the graph obtained from R by changing the edge weight of
$R_i$
be the graph obtained from R by changing the edge weight of
![]() $(v_{3-i},u)$
to
$(v_{3-i},u)$
to
![]() $w(v_i,u)$
for all
$w(v_i,u)$
for all
![]() $u\in V(R)\setminus \{v_1,v_2\}$
, and changing the vertex weights of both
$u\in V(R)\setminus \{v_1,v_2\}$
, and changing the vertex weights of both
![]() $v_1$
and
$v_1$
and
![]() $v_2$
to
$v_2$
to
![]() $\frac {w(v_1)+w(v_2)}{2}$
. We claim that
$\frac {w(v_1)+w(v_2)}{2}$
. We claim that
![]() $R_1$
and
$R_1$
and
![]() $R_2$
are
$R_2$
are
![]() ${ \mathcal {K}}_t$
-free. Indeed, suppose that
${ \mathcal {K}}_t$
-free. Indeed, suppose that
![]() $R_1$
contains a weighted t-clique
$R_1$
contains a weighted t-clique
![]() $(S_1,S_2)$
with
$(S_1,S_2)$
with
![]() $S_2\subseteq S_1\subseteq V(R_1)$
and
$S_2\subseteq S_1\subseteq V(R_1)$
and
![]() $|S_1|+|S_2|=t$
. Because
$|S_1|+|S_2|=t$
. Because
![]() $w(v_1,v_2)=\frac 12$
in
$w(v_1,v_2)=\frac 12$
in
![]() $R_1$
, the set
$R_1$
, the set
![]() $S_2$
cannot contain both
$S_2$
cannot contain both
![]() $v_1$
and
$v_1$
and
![]() $v_2$
; as these vertices are indistinguishable in
$v_2$
; as these vertices are indistinguishable in
![]() $R_i$
, we may assume that
$R_i$
, we may assume that
![]() $S_2$
does not contain
$S_2$
does not contain
![]() $v_2$
. Hence,
$v_2$
. Hence,
![]() $R_1$
and R have the same edge weights between vertices of
$R_1$
and R have the same edge weights between vertices of
![]() $S_2$
. Furthermore, all edge weights of R (and in particular, all edge weights between vertices of
$S_2$
. Furthermore, all edge weights of R (and in particular, all edge weights between vertices of
![]() $S_1$
) are positive because R satisfies (A1). It follows that
$S_1$
) are positive because R satisfies (A1). It follows that
![]() $S_1$
and
$S_1$
and
![]() $S_2$
form a weighted t-clique in R, a contradiction. The proof that
$S_2$
form a weighted t-clique in R, a contradiction. The proof that
![]() $R_2$
is
$R_2$
is
![]() ${ \mathcal {K}}_t$
-free is analogous.
${ \mathcal {K}}_t$
-free is analogous.
Write
![]() $\alpha _i= \frac {w(v_i)}{w(v_1)+w(v_2)}$
for
$\alpha _i= \frac {w(v_i)}{w(v_1)+w(v_2)}$
for
![]() $i\in [2]$
as in (3.1). We see that
$i\in [2]$
as in (3.1). We see that

To compare
![]() $d_{K_s}(R,\{v_1,v_2\})$
and
$d_{K_s}(R,\{v_1,v_2\})$
and
![]() $d_{K_s}(R_i,\{v_1,v_2\})$
, let
$d_{K_s}(R_i,\{v_1,v_2\})$
, let
![]() $S=\{v_1,\ldots ,v_s\}\subseteq V(R)$
be any set of s vertices containing
$S=\{v_1,\ldots ,v_s\}\subseteq V(R)$
be any set of s vertices containing
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. We observe that
$v_2$
. We observe that

where
![]() $W_1:=\prod _{i=3}^{s}w(v_1,v_i)$
,
$W_1:=\prod _{i=3}^{s}w(v_1,v_i)$
,
![]() $W_2:=\prod _{i=3}^{s}w(v_2,v_i)$
, and
$W_2:=\prod _{i=3}^{s}w(v_2,v_i)$
, and ![]() . Furthermore, by the AM-GM inequality, we have
. Furthermore, by the AM-GM inequality, we have

with equality if and only if
![]() $w(v_1)=w(v_2)$
and
$w(v_1)=w(v_2)$
and
![]() $W_1=W_2$
.
$W_1=W_2$
.
Summing over all such sets S, we have

Moreover, equality holds if and only if
![]() $w(v_1)=w(v_2)$
and
$w(v_1)=w(v_2)$
and
![]() $W_1=W_2$
for all sets S. We claim that this condition implies that
$W_1=W_2$
for all sets S. We claim that this condition implies that
![]() $w(v_1,u)=w(v_2,u)$
for each
$w(v_1,u)=w(v_2,u)$
for each
![]() $u\in V(R)-\{v_1,v_2\}$
. Indeed, because all edge weights are either
$u\in V(R)-\{v_1,v_2\}$
. Indeed, because all edge weights are either
![]() $1/2$
or
$1/2$
or
![]() $1$
, it follows that
$1$
, it follows that

for any
![]() $s-2$
distinct vertices
$s-2$
distinct vertices
![]() $v_3,\ldots ,v_s\in V(R)-\{v_1,v_2\}$
. Letting
$v_3,\ldots ,v_s\in V(R)-\{v_1,v_2\}$
. Letting
![]() $\mathbf w^{(1)},\mathbf w^{(2)}\in \mathbb \{\frac 12,1\}^{b-2}$
be vectors defined as
$\mathbf w^{(1)},\mathbf w^{(2)}\in \mathbb \{\frac 12,1\}^{b-2}$
be vectors defined as
![]() $\mathbf w^{(i)}_u=w(v_i,u)$
for
$\mathbf w^{(i)}_u=w(v_i,u)$
for
![]() $u\in V(R)-\{v_1,v_2\}$
, this yields a linear relation
$u\in V(R)-\{v_1,v_2\}$
, this yields a linear relation
![]() $\mathbf v\cdot \mathbf w^{(1)}=\mathbf v\cdot \mathbf w^{(2)}$
, where
$\mathbf v\cdot \mathbf w^{(1)}=\mathbf v\cdot \mathbf w^{(2)}$
, where
![]() $\mathbf v\in \mathbb R^{b-2}$
is the indicator vector of
$\mathbf v\in \mathbb R^{b-2}$
is the indicator vector of
![]() $\{v_3,\ldots ,v_s\}$
. When
$\{v_3,\ldots ,v_s\}$
. When
![]() $b>s$
, the vectors
$b>s$
, the vectors
![]() $\mathbf v$
span
$\mathbf v$
span
![]() $\mathbb R^{b-2}$
, and it follows that
$\mathbb R^{b-2}$
, and it follows that
![]() $\mathbf w^{(1)}=\mathbf w^{(2)}$
.
$\mathbf w^{(1)}=\mathbf w^{(2)}$
.
We conclude that
![]() $\alpha _1\cdot d_{K_s}(R_1)+\alpha _2\cdot d_{K_s}(R_2)\geq d_{K_s}(R)$
, with equality only if
$\alpha _1\cdot d_{K_s}(R_1)+\alpha _2\cdot d_{K_s}(R_2)\geq d_{K_s}(R)$
, with equality only if
![]() $w(v_1)=w(v_2)$
and
$w(v_1)=w(v_2)$
and
![]() $w(v_1,u)=w(v_2,u)$
for any third vertex u. Because R is extremal, it follows that any
$w(v_1,u)=w(v_2,u)$
for any third vertex u. Because R is extremal, it follows that any
![]() $v_1,v_2\in V(R)$
with
$v_1,v_2\in V(R)$
with
![]() $w(v_1,v_2)=1/2$
must satisfy these conditions. This implies that
$w(v_1,v_2)=1/2$
must satisfy these conditions. This implies that
![]() $V(R)$
may be partitioned into
$V(R)$
may be partitioned into
![]() $B_1\cup \cdots \cup B_a$
such that vertices within each part have the same weights, and edges have weight
$B_1\cup \cdots \cup B_a$
such that vertices within each part have the same weights, and edges have weight
![]() $1/2$
if they lie within some part
$1/2$
if they lie within some part
![]() $B_i$
and weight
$B_i$
and weight
![]() $1$
otherwise.
$1$
otherwise.
Lastly, we show that if R is extremal and
![]() $V(R)$
admits such a partition
$V(R)$
admits such a partition
![]() $B_1\cup \cdots \cup B_a$
then
$B_1\cup \cdots \cup B_a$
then
![]() $a+b=t-1$
, where
$a+b=t-1$
, where
![]() $b=|V(R)|\geq s$
. If
$b=|V(R)|\geq s$
. If
![]() $a+b\geq t$
then we may form a weighted t-clique
$a+b\geq t$
then we may form a weighted t-clique
![]() $(S_1,S_2)$
by setting
$(S_1,S_2)$
by setting
![]() $S_1=V(R)$
and letting
$S_1=V(R)$
and letting
![]() $S_2$
contain one vertex from each of
$S_2$
contain one vertex from each of
![]() $B_1,\ldots ,B_{t-b}$
. If
$B_1,\ldots ,B_{t-b}$
. If
![]() $a+b\leq t-2$
then we claim that R is not extremal. Choose a vertex
$a+b\leq t-2$
then we claim that R is not extremal. Choose a vertex
![]() $v\in B_1$
and let
$v\in B_1$
and let
![]() $R'$
be the weighted graph obtained from R by replacing v with two vertices
$R'$
be the weighted graph obtained from R by replacing v with two vertices
![]() $v_1,v_2$
of weight
$v_1,v_2$
of weight
![]() $\frac {w(v)}2$
, setting
$\frac {w(v)}2$
, setting
![]() $w(v_1,v_2)=1/2$
and
$w(v_1,v_2)=1/2$
and
![]() $w(v_i,u)=w(v,u)$
for
$w(v_i,u)=w(v,u)$
for
![]() $u\in V(R)-\{v\}$
and
$u\in V(R)-\{v\}$
and
![]() $i\in [2]$
. We note that
$i\in [2]$
. We note that
![]() $R'$
is
$R'$
is
![]() $\mathcal K_t$
-free:
$\mathcal K_t$
-free:
![]() $R^{\prime }_{>1/2}$
is
$R^{\prime }_{>1/2}$
is
![]() $K_{a+1}$
-free, so for any weighted clique
$K_{a+1}$
-free, so for any weighted clique
![]() $(S_1,S_2)$
in
$(S_1,S_2)$
in
![]() $R'$
, we have
$R'$
, we have
![]() $|S_1|+|S_2|\leq |V(R')|+a=b+1+a\leq t-1$
. Moreover, it is clear that
$|S_1|+|S_2|\leq |V(R')|+a=b+1+a\leq t-1$
. Moreover, it is clear that
![]() $d_{K_s}(R')>d_{K_s}(R)$
, contradicting the extremality of R. It follows that
$d_{K_s}(R')>d_{K_s}(R)$
, contradicting the extremality of R. It follows that
![]() $a+b=t-1$
, as desired.
$a+b=t-1$
, as desired.
3.3 Proof of (A3) and (A4) for
 $a=2$
$a=2$
We first prove (A3) and (A4) for weighted graphs R satisfying (A2) with
![]() $a=2$
parts. For convenience, we introduce the following notation. Given positive integers
$a=2$
parts. For convenience, we introduce the following notation. Given positive integers
![]() $P,Q$
and real numbers
$P,Q$
and real numbers
![]() $p,q\in (0,1)$
satisfying
$p,q\in (0,1)$
satisfying
![]() $pP+qQ=1$
, let
$pP+qQ=1$
, let
![]() $R(p,P;q,Q)$
denote the
$R(p,P;q,Q)$
denote the
![]() $(P+Q)$
-vertex weighted graph satisfying (A2) with parameters
$(P+Q)$
-vertex weighted graph satisfying (A2) with parameters
![]() $a=2$
,
$a=2$
,
![]() $|B_1|=P$
, and
$|B_1|=P$
, and
![]() $|B_2|=Q$
, such that
$|B_2|=Q$
, such that
![]() $w(v_1)=p$
and
$w(v_1)=p$
and
![]() $w(v_2)=q$
for any vertex
$w(v_2)=q$
for any vertex
![]() $v_1\in B_1$
or
$v_1\in B_1$
or
![]() $v_2\in B_2$
.
$v_2\in B_2$
.
In Lemmas 3.3, 3.5 and 3.8 below, we show that if
![]() $R=R(p,P;q,Q)$
does not satisfy (A3) or (A4) then there is another weighted graph
$R=R(p,P;q,Q)$
does not satisfy (A3) or (A4) then there is another weighted graph
![]() $R'$
on
$R'$
on
![]() $P+Q$
vertices such that
$P+Q$
vertices such that
![]() $R^{\prime }_{>\frac 12}$
is also bipartite and
$R^{\prime }_{>\frac 12}$
is also bipartite and
![]() $d_{K_m}(R')>d_{K_m}(R)$
for all m in the range
$d_{K_m}(R')>d_{K_m}(R)$
for all m in the range
![]() $2\leq m\leq P+Q$
. This is a slightly stronger statement than necessary to handle the
$2\leq m\leq P+Q$
. This is a slightly stronger statement than necessary to handle the
![]() $a=2$
case, but it will prove necessary when we consider
$a=2$
case, but it will prove necessary when we consider
![]() $a\geq 3$
in the next subsection.
$a\geq 3$
in the next subsection.
Lemma 3.3. Let
![]() $P,Q$
be positive integers and
$P,Q$
be positive integers and
![]() $p,q\in (0,1)$
real numbers such that
$p,q\in (0,1)$
real numbers such that
![]() $pP+qQ=1$
. If
$pP+qQ=1$
. If
![]() $P\geq Q+1$
and
$P\geq Q+1$
and
![]() $(P-1)p>Qq$
, then there exists a weighted graph
$(P-1)p>Qq$
, then there exists a weighted graph
![]() $R'$
with
$R'$
with
![]() $P+Q$
vertices such that
$P+Q$
vertices such that
![]() $R^{\prime }_{>\frac 12}$
is bipartite and
$R^{\prime }_{>\frac 12}$
is bipartite and
![]() $d_{K_m}(R(p,P;q,Q))< d_{K_m}(R')$
for all
$d_{K_m}(R(p,P;q,Q))< d_{K_m}(R')$
for all
![]() $2\leq m\leq P+Q$
.
$2\leq m\leq P+Q$
.
Proof. Set
![]() $R = R(p,P;q,Q)$
and let u be a vertex in R with weight p. Let
$R = R(p,P;q,Q)$
and let u be a vertex in R with weight p. Let
![]() $R'$
be the graph obtained from R by changing the weights of all edges incident to u: if
$R'$
be the graph obtained from R by changing the weights of all edges incident to u: if
![]() $(u,v)$
has edge weight
$(u,v)$
has edge weight
![]() $w\in \{\frac 12,1\}$
in R, then we assign it the weight
$w\in \{\frac 12,1\}$
in R, then we assign it the weight
![]() $\frac 32-w$
in
$\frac 32-w$
in
![]() $R'$
. It is clear that
$R'$
. It is clear that
![]() $R^{\prime }_{>\frac 12}$
is a complete bipartite graph with parts of size
$R^{\prime }_{>\frac 12}$
is a complete bipartite graph with parts of size
![]() $P-1$
and
$P-1$
and
![]() $Q+1$
.
$Q+1$
.
Fix m with
![]() $2\leq m\leq P+Q$
. We verify that
$2\leq m\leq P+Q$
. We verify that
![]() $d_{K_m}(R,u)<d_{K_m}(R',u)$
. We have that
$d_{K_m}(R,u)<d_{K_m}(R',u)$
. We have that

Let ![]() . If
. If
![]() $x\ge y$
then
$x\ge y$
then

with equality only if
![]() $x=y$
. This in turn implies that
$x=y$
. This in turn implies that

for any
![]() $x,y$
, again with equality only if
$x,y$
, again with equality only if
![]() $x=y$
. Thus,
$x=y$
. Thus,

To conclude the proof, we observe that
![]() $d_{K_m}(R-u)=d_{K_m}(R'-u)$
, and thus
$d_{K_m}(R-u)=d_{K_m}(R'-u)$
, and thus
Next, we handle (A3) in the case that
![]() $(P-1)p\leq Qq$
. To help us bound
$(P-1)p\leq Qq$
. To help us bound
![]() $d_{K_m}(R(p,P;q,Q))$
in this case, we shall write it in terms of the following quantities. Given integers
$d_{K_m}(R(p,P;q,Q))$
in this case, we shall write it in terms of the following quantities. Given integers
![]() $m,r$
with
$m,r$
with
![]() $0\leq r\leq m/2$
, define
$0\leq r\leq m/2$
, define

Intuitively,
![]() $N_{m,r}$
should be thought of as counting copies of
$N_{m,r}$
should be thought of as counting copies of
![]() $K_m$
in
$K_m$
in
![]() $R(p,P;q,Q)$
with r labeled vertices in each part. We now show that
$R(p,P;q,Q)$
with r labeled vertices in each part. We now show that
![]() $d_{K_m}(R(p,P;q,Q))$
is a positive linear combination of these quantities.
$d_{K_m}(R(p,P;q,Q))$
is a positive linear combination of these quantities.
Lemma 3.4. Fix a positive integer m. There exist constants
![]() $c_{r}>0$
for
$c_{r}>0$
for
![]() $0\leq r\leq \lfloor m/2\rfloor $
such that
$0\leq r\leq \lfloor m/2\rfloor $
such that

for any
![]() $P,Q,p,q$
.
$P,Q,p,q$
.
Proof. Observe that each
![]() $N_{m,r}$
is a linear combination of the
$N_{m,r}$
is a linear combination of the
![]() $\left \lfloor \frac m2\right \rfloor +1$
polynomials
$\left \lfloor \frac m2\right \rfloor +1$
polynomials

with nonzero coefficient if and only if
![]() $x\geq r$
. Thus,
$x\geq r$
. Thus,
![]() $\{N_{m,r}:0\leq r\leq m/2\}$
is a basis for the space of all linear combinations of these polynomials, which includes the
$\{N_{m,r}:0\leq r\leq m/2\}$
is a basis for the space of all linear combinations of these polynomials, which includes the
![]() $K_m$
-density
$K_m$
-density

It follows that there exist real numbers
![]() $c_{r}$
such that
$c_{r}$
such that

Moreover, by setting the coefficients of the rth term equal to each other, we conclude that

for each
![]() $r\leq m/2$
.
$r\leq m/2$
.
We show that the coefficients
![]() $c_{r}$
are positive by induction on r. Clearly,
$c_{r}$
are positive by induction on r. Clearly,
![]() $c_0> 0$
by (3.2) when
$c_0> 0$
by (3.2) when
![]() $r=0$
. Now, suppose
$r=0$
. Now, suppose
![]() $c_i> 0$
for all
$c_i> 0$
for all
![]() $i<r$
. By (3.2), we have
$i<r$
. By (3.2), we have

We claim that
for each
![]() $i<r$
. Indeed, it suffices to show that
$i<r$
. Indeed, it suffices to show that
which, recalling that
![]() $r\leq m/2$
, follows from the inequalities
$r\leq m/2$
, follows from the inequalities
![]() $2^{m-2r+1}\geq m-2r+2$
and
$2^{m-2r+1}\geq m-2r+2$
and
![]() $\frac {r-i}{m-r+1-i}=\frac {r-i}{m-2r+1+(r-i)}\geq \frac {1}{m-2r+2}$
. Hence,
$\frac {r-i}{m-r+1-i}=\frac {r-i}{m-2r+1+(r-i)}\geq \frac {1}{m-2r+2}$
. Hence,

which implies
![]() $c_r>0$
.
$c_r>0$
.
Using Lemma 3.4, we handle (A3) in the case that
![]() $(P-1)p\leq Qq$
.
$(P-1)p\leq Qq$
.
Lemma 3.5. Let
![]() $P,Q$
be positive integers with
$P,Q$
be positive integers with
![]() $P\geq Q+2$
and let
$P\geq Q+2$
and let
![]() $p,q\in (0,1)$
be real numbers such that
$p,q\in (0,1)$
be real numbers such that
![]() $Pp+Qq=1$
. Set
$Pp+Qq=1$
. Set
![]() $P'=P-1$
,
$P'=P-1$
,
![]() $Q'=Q+1$
, and choose
$Q'=Q+1$
, and choose
![]() $p',q'\in (0,1)$
such that
$p',q'\in (0,1)$
such that
![]() $P'p'=Pp$
and
$P'p'=Pp$
and
![]() $Q'q'=Qq$
. If
$Q'q'=Qq$
. If
![]() $(P-1)p\le Qq$
then
$(P-1)p\le Qq$
then
![]() $d_{K_m}(R(p,P;q,Q))< d_{K_m}(R(p',P';q',Q'))$
for all
$d_{K_m}(R(p,P;q,Q))< d_{K_m}(R(p',P';q',Q'))$
for all
![]() $2\leq m\leq P+Q$
.
$2\leq m\leq P+Q$
.
Proof. Set
![]() $R=R(p,P;q,Q)$
and
$R=R(p,P;q,Q)$
and
![]() $R'=R(p',P';q',Q')$
, and fix m with
$R'=R(p',P';q',Q')$
, and fix m with
![]() $2\leq m\leq P+Q$
. For convenience, we write
$2\leq m\leq P+Q$
. For convenience, we write
![]() $N_{m,r}(R)=N_{m,r}(p,P;q,Q)$
and
$N_{m,r}(R)=N_{m,r}(p,P;q,Q)$
and
![]() $N_{m,r}(R')=N_{m,r}(p',P';q',Q')$
.
$N_{m,r}(R')=N_{m,r}(p',P';q',Q')$
.
By Lemma 3.4, it suffices to compare
![]() $N_{m,r}(R)$
and
$N_{m,r}(R)$
and
![]() $ N_{m,r}(R')$
. We begin with some preliminary inequalities. Let
$ N_{m,r}(R')$
. We begin with some preliminary inequalities. Let
![]() $p_-=\min \{p',q'\}$
and
$p_-=\min \{p',q'\}$
and
![]() $p_+=\max \{p',q'\}$
.
$p_+=\max \{p',q'\}$
.
Claim 3.6. We have the following inequalities.
-
(1) For any
 $0<r \le |Q|$
, we have
$0<r \le |Q|$
, we have
 $(1-\frac {r}{P})(1-\frac {r}{Q})< (1-\frac {r}{P'})(1-\frac {r}{Q'})$
.
$(1-\frac {r}{P})(1-\frac {r}{Q})< (1-\frac {r}{P'})(1-\frac {r}{Q'})$
. -
(2)
 $p\leq p_-\leq p_+<q$
.
$p\leq p_-\leq p_+<q$
. -
(3) For any
 $0<r\leq |Q|$
, we have
$0<r\leq |Q|$
, we have
 $(P-r)p+(Q-r)q<(P'-r)p'+(Q'-r)q'$
.
$(P-r)p+(Q-r)q<(P'-r)p'+(Q'-r)q'$
.
Proof of claim
(1) Because
![]() $P\geq Q+2$
, we have
$P\geq Q+2$
, we have

(2) Using the relation
![]() $(P-1)p\leq Qq$
, it follows that
$(P-1)p\leq Qq$
, it follows that
![]() $p<\frac {P}{P-1}p=p'\leq \frac {PQ}{(P-1)^2}q<q$
and that
$p<\frac {P}{P-1}p=p'\leq \frac {PQ}{(P-1)^2}q<q$
and that
![]() $q>\frac {Qq}{Q+1}=q'\geq \frac {(P-1)p}{Q+1}\geq p$
.
$q>\frac {Qq}{Q+1}=q'\geq \frac {(P-1)p}{Q+1}\geq p$
.
(3) First, observe that
because
![]() $p\leq Qq/(P-1)<q$
. Thus,
$p\leq Qq/(P-1)<q$
. Thus,
if
![]() $r>0$
.
$r>0$
.
We now compare
![]() $N_{m,r}(R)$
and
$N_{m,r}(R)$
and
![]() $N_{m,r}(R')$
.
$N_{m,r}(R')$
.
Claim 3.7. We have
![]() $N_{m,r}(R)\leq N_{m,r}(R')$
for any
$N_{m,r}(R)\leq N_{m,r}(R')$
for any
![]() $0\leq r\leq \lfloor m/2\rfloor $
. Moreover, the inequality is strict when
$0\leq r\leq \lfloor m/2\rfloor $
. Moreover, the inequality is strict when
![]() $r>0$
.
$r>0$
.
Proof of claim
By Claim 3.6(1),

with equality only if
![]() $r=0$
. It remains to show that
$r=0$
. It remains to show that

Set
 $X = (\underbrace {p,p ,\ldots , p }_{P-r}, \underbrace {q,q ,\ldots ,q}_{Q-r})$
and
$X = (\underbrace {p,p ,\ldots , p }_{P-r}, \underbrace {q,q ,\ldots ,q}_{Q-r})$
and
 $X' = (\underbrace {p',p' ,\ldots , p' }_{P-r-1}, \underbrace {q',q' ,\ldots ,q'}_{Q-r+1})$
. Letting
$X' = (\underbrace {p',p' ,\ldots , p' }_{P-r-1}, \underbrace {q',q' ,\ldots ,q'}_{Q-r+1})$
. Letting
![]() $\sigma $
be the
$\sigma $
be the
![]() $(m-2r)$
th elementary symmetric function
$(m-2r)$
th elementary symmetric function
we may rewrite (3.3) as
![]() $\sigma (X)\leq \sigma (X')$
.
$\sigma (X)\leq \sigma (X')$
.
Let Y be the
![]() $(P+Q-2r)$
-tuple obtained via the following process. Set
$(P+Q-2r)$
-tuple obtained via the following process. Set
![]() $Y=X$
initially and repeat the following transformation, which will never decrease
$Y=X$
initially and repeat the following transformation, which will never decrease
![]() $\sigma (Y)$
.
$\sigma (Y)$
.
-
(*) If there exist indices
 $i,j$
such that
$i,j$
such that
 $Y_i<p_-$
and
$Y_i<p_-$
and
 $Y_j>p_+$
, set
$Y_j>p_+$
, set
 $\varepsilon =\min \{p_--Y_i,~Y_j-p_+\}$
, and replace
$\varepsilon =\min \{p_--Y_i,~Y_j-p_+\}$
, and replace
 $Y_i$
and
$Y_i$
and
 $Y_j$
with
$Y_j$
with
 $Y_i+\varepsilon $
and
$Y_i+\varepsilon $
and
 $Y_j-\varepsilon $
, respectively.
$Y_j-\varepsilon $
, respectively.
Each iteration increases the number of coordinates equal to
![]() $p_-$
or
$p_-$
or
![]() $p_+$
, so the process will terminate in at most
$p_+$
, so the process will terminate in at most
![]() $P+Q-2r$
steps. Moreover, recalling that
$P+Q-2r$
steps. Moreover, recalling that
![]() $p\leq p_-\leq p_+<q$
, we observe that the final tuple Y either takes the form
$p\leq p_-\leq p_+<q$
, we observe that the final tuple Y either takes the form

Let
![]() $X" = (p_-,\ldots ,p_-,p_+,\ldots ,p_+)$
be the result of sorting
$X" = (p_-,\ldots ,p_-,p_+,\ldots ,p_+)$
be the result of sorting
![]() $X'$
in increasing order, and let
$X'$
in increasing order, and let
![]() $k\in \{P-r-1, Q-r+1\}$
be the number of occurrences of
$k\in \{P-r-1, Q-r+1\}$
be the number of occurrences of
![]() $p_-$
. In case 1, we have
$p_-$
. In case 1, we have
![]() $Y_i\leq X^{\prime \prime }_i$
for each i, implying
$Y_i\leq X^{\prime \prime }_i$
for each i, implying
![]() $\sigma (Y)\leq \sigma (X")$
. In case 2, let y be the average value of
$\sigma (Y)\leq \sigma (X")$
. In case 2, let y be the average value of
![]() $\{Y_{k+1},\ldots ,Y_{P+Q-2r}\}$
and let
$\{Y_{k+1},\ldots ,Y_{P+Q-2r}\}$
and let
![]() $Y'=(p_-,\ldots ,p_-,y,\ldots ,y)$
be the result of replacing all but the first k terms of Y with y. By Lemma 3.2,
$Y'=(p_-,\ldots ,p_-,y,\ldots ,y)$
be the result of replacing all but the first k terms of Y with y. By Lemma 3.2,
![]() $\sigma (Y)\leq \sigma (Y')$
. Moreover,
$\sigma (Y)\leq \sigma (Y')$
. Moreover,
![]() $\mathrm {sum}(Y')=\mathrm {sum}(X)<\mathrm {sum}(X")$
by Claim 3.6(3). Because
$\mathrm {sum}(Y')=\mathrm {sum}(X)<\mathrm {sum}(X")$
by Claim 3.6(3). Because
![]() $X"$
is obtained from
$X"$
is obtained from
![]() $Y'$
by replacing each y with
$Y'$
by replacing each y with
![]() $p_+$
, it follows that
$p_+$
, it follows that
![]() $y<p_+$
and
$y<p_+$
and
![]() $\sigma (Y')<\sigma (X")$
. Thus, we have
$\sigma (Y')<\sigma (X")$
. Thus, we have
![]() $\sigma (X)\leq \sigma (Y)\leq \sigma (X")=\sigma (X')$
in both cases, completing the proof that
$\sigma (X)\leq \sigma (Y)\leq \sigma (X")=\sigma (X')$
in both cases, completing the proof that
![]() $N_{m,r}(R)\leq N_{m,r}(R')$
.
$N_{m,r}(R)\leq N_{m,r}(R')$
.
Combining Lemma 3.4 and Claim 3.7, we have that

Lastly, we turn our attention to (A4). If
![]() $P>Q$
, this is an immediate consequence of Lemma 3.3; it remains to handle the
$P>Q$
, this is an immediate consequence of Lemma 3.3; it remains to handle the
![]() $P=Q$
case.
$P=Q$
case.
Lemma 3.8. Let P be a positive integer and
![]() $p,q\in (0,1)$
real numbers such that
$p,q\in (0,1)$
real numbers such that
![]() $pP+qP=1$
. If
$pP+qP=1$
. If
![]() $p\neq q$
, then there exists a weighted graph
$p\neq q$
, then there exists a weighted graph
![]() $R'$
with
$R'$
with
![]() $2P$
vertices such that
$2P$
vertices such that
![]() $R^{\prime }_{>\frac 12}$
is bipartite and
$R^{\prime }_{>\frac 12}$
is bipartite and
![]() $d_{K_m}(R(p,P;q,P))< d_{K_m}(R')$
for all
$d_{K_m}(R(p,P;q,P))< d_{K_m}(R')$
for all
![]() $2\leq m\leq 2P$
.
$2\leq m\leq 2P$
.
Proof. Set
![]() $R=R(p,P;q,P)$
and let u and v be vertices in R with weights p and q, respectively. Let
$R=R(p,P;q,P)$
and let u and v be vertices in R with weights p and q, respectively. Let
![]() $R'$
be the graph obtained from R by setting the weights of both u and v to
$R'$
be the graph obtained from R by setting the weights of both u and v to
![]() $\frac {p+q}2=\frac 1{2P}$
.
$\frac {p+q}2=\frac 1{2P}$
.
Observe that
![]() $d_{K_m}(R-\{u,v\})=d_{K_m}(R'-\{u,v\})$
. Set
$d_{K_m}(R-\{u,v\})=d_{K_m}(R'-\{u,v\})$
. Set

We have that

because
![]() $q-p$
and
$q-p$
and
![]() $q^{y-x}-p^{y-x}$
both have the same sign. Additionally,
$q^{y-x}-p^{y-x}$
both have the same sign. Additionally,

Combining the preceding inequalities, we conclude that

for any integer
![]() $2\leq m\leq 2P$
.
$2\leq m\leq 2P$
.
3.4 Proof of (A3) and (A4) for all a
Using the results of the prior subsection, we prove (A3) and (A4) for all a. Suppose R is an extremal
![]() $\mathcal K_t$
-free weighted graph satisfying (A1) and (A2) with parts
$\mathcal K_t$
-free weighted graph satisfying (A1) and (A2) with parts
![]() $B_1,\ldots ,B_a$
. Given indices
$B_1,\ldots ,B_a$
. Given indices
![]() $i\neq j$
, we may regard
$i\neq j$
, we may regard
![]() $R[B_i\cup B_j]$
as a scaled-down version of some weighted graph
$R[B_i\cup B_j]$
as a scaled-down version of some weighted graph
![]() $R_0=R(p,|B_i|;q,|B_j|)$
, where the weights of vertices in
$R_0=R(p,|B_i|;q,|B_j|)$
, where the weights of vertices in
![]() $B_i$
and
$B_i$
and
![]() $B_j$
are
$B_j$
are
![]() $\alpha p$
and
$\alpha p$
and
![]() $\alpha q$
respectively, for some
$\alpha q$
respectively, for some
![]() $\alpha \leq 1$
.
$\alpha \leq 1$
.
Without loss of generality, suppose
![]() $|B_i|\geq |B_j|$
. We claim that
$|B_i|\geq |B_j|$
. We claim that
![]() $|B_i|\leq |B_j|+1$
and that
$|B_i|\leq |B_j|+1$
and that
![]() $p\leq q$
. Indeed, if
$p\leq q$
. Indeed, if
![]() $|B_i|\geq |B_j|+2$
then Lemma 3.3 or Lemma 3.5 yields a weighted graph
$|B_i|\geq |B_j|+2$
then Lemma 3.3 or Lemma 3.5 yields a weighted graph
![]() $R^{\prime }_0$
on
$R^{\prime }_0$
on
![]() $|B_i|+|B_j|$
vertices such that
$|B_i|+|B_j|$
vertices such that
![]() $(R^{\prime }_0)_{>\frac 12}$
is bipartite and
$(R^{\prime }_0)_{>\frac 12}$
is bipartite and
![]() $d_{K_m}(R^{\prime }_0)> d_{K_m}(R_0)$
for all
$d_{K_m}(R^{\prime }_0)> d_{K_m}(R_0)$
for all
![]() $2\leq m\leq |B_i|+|B_j|$
. Note that
$2\leq m\leq |B_i|+|B_j|$
. Note that
![]() $d_{K_m}(R_0)=d_{K_m}(R^{\prime }_0)$
for all other m: this value is 1 if
$d_{K_m}(R_0)=d_{K_m}(R^{\prime }_0)$
for all other m: this value is 1 if
![]() $m=1$
and 0 if
$m=1$
and 0 if
![]() $m>|B_i|+|B_j|$
. If
$m>|B_i|+|B_j|$
. If
![]() $p>q$
, then Lemma 3.3 (if
$p>q$
, then Lemma 3.3 (if
![]() $|B_i|>|B_j|$
) or Lemma 3.8 (if
$|B_i|>|B_j|$
) or Lemma 3.8 (if
![]() $|B_i|=|B_j|$
) provides a weighted graph
$|B_i|=|B_j|$
) provides a weighted graph
![]() $R^{\prime }_0$
with the same properties.
$R^{\prime }_0$
with the same properties.
Let
![]() $R'$
be the weighted graph obtained from R by replacing
$R'$
be the weighted graph obtained from R by replacing
![]() $R[B_i\cup B_j]$
with a scaled-down copy of
$R[B_i\cup B_j]$
with a scaled-down copy of
![]() $R^{\prime }_0$
. That is, the vertex weights of
$R^{\prime }_0$
. That is, the vertex weights of
![]() $R'[B_i\cup B_j]$
are those of
$R'[B_i\cup B_j]$
are those of
![]() $R^{\prime }_0$
multiplied by
$R^{\prime }_0$
multiplied by
![]() $\alpha $
, and the edge weights of
$\alpha $
, and the edge weights of
![]() $R'[B_i\cup B_j]$
are exactly those of
$R'[B_i\cup B_j]$
are exactly those of
![]() $R^{\prime }_0$
. We verify that
$R^{\prime }_0$
. We verify that
![]() $R'$
is
$R'$
is
![]() $\mathcal K_t$
-free. Suppose
$\mathcal K_t$
-free. Suppose
![]() $(S_1,S_2)$
is a weighted clique in
$(S_1,S_2)$
is a weighted clique in
![]() $R'$
. Because
$R'$
. Because
![]() $\left (R^{\prime }_0\right )_{>1/2}$
is bipartite,
$\left (R^{\prime }_0\right )_{>1/2}$
is bipartite,
![]() $S_2$
contains at most two vertices of
$S_2$
contains at most two vertices of
![]() $B_i\cup B_j$
; additionally,
$B_i\cup B_j$
; additionally,
![]() $S_2$
contains at most one vertex from each other part
$S_2$
contains at most one vertex from each other part
![]() $B_k$
. Hence
$B_k$
. Hence
![]() $|S_1|+|S_2|\leq |V(R)|+a=b+a=t-1$
, so
$|S_1|+|S_2|\leq |V(R)|+a=b+a=t-1$
, so
![]() $R'$
is
$R'$
is
![]() $\mathcal K_t$
-free. However, because
$\mathcal K_t$
-free. However, because
we have that

Thus, if the parts
![]() $(B_i,B_j)$
do not satisfy (A3) or (A4) then
$(B_i,B_j)$
do not satisfy (A3) or (A4) then
![]() $d_{K_s}(R)<d_{K_s}(R')$
, contradicting the extremality of R.
$d_{K_s}(R)<d_{K_s}(R')$
, contradicting the extremality of R.
3.5 Proof of (A5)
Suppose that R is an extremal
![]() $\mathcal K_t$
-free weighted graph satisfying (A1) and thus (A2)–(A4) with parts
$\mathcal K_t$
-free weighted graph satisfying (A1) and thus (A2)–(A4) with parts
![]() $B_1,\ldots ,B_a$
. Without loss of generality, suppose
$B_1,\ldots ,B_a$
. Without loss of generality, suppose
![]() $B_1$
has maximal cardinality among all parts
$B_1$
has maximal cardinality among all parts
![]() $B_i$
. We assume that
$B_i$
. We assume that
![]() $r=|B_1|$
satisfies
$r=|B_1|$
satisfies
![]() $r\geq s+1$
(if
$r\geq s+1$
(if
![]() $a=1$
) or
$a=1$
) or
![]() $r\geq s$
(if
$r\geq s$
(if
![]() $a\geq 2$
) and derive a contradiction.
$a\geq 2$
) and derive a contradiction.
Let p be the weight of each vertex in
![]() $B_1$
; by (A4), it follows that all vertices of R have weight at least p. Let
$B_1$
; by (A4), it follows that all vertices of R have weight at least p. Let
![]() $R'$
be the graph obtained from R by replacing two vertices
$R'$
be the graph obtained from R by replacing two vertices
![]() $u,v\in B_1$
with a new vertex
$u,v\in B_1$
with a new vertex
![]() $v'$
of weight
$v'$
of weight
![]() $2p$
and setting
$2p$
and setting
![]() $w(v',u')=1$
for any
$w(v',u')=1$
for any
![]() $u'\in V(R')\setminus \{v'\}$
. We observe that
$u'\in V(R')\setminus \{v'\}$
. We observe that
![]() $R'$
is
$R'$
is
![]() $\mathcal K_t$
-free. Indeed, if
$\mathcal K_t$
-free. Indeed, if
![]() $(S_1,S_2)$
is a weighted clique configuration in
$(S_1,S_2)$
is a weighted clique configuration in
![]() $R'$
then
$R'$
then
![]() $S_2$
may contain at most one vertex from each of the sets
$S_2$
may contain at most one vertex from each of the sets
![]() $\{v'\},B_1-\{u,v\},B_2,\ldots ,B_a$
. It follows that
$\{v'\},B_1-\{u,v\},B_2,\ldots ,B_a$
. It follows that
![]() $|S_1|+|S_2|\leq |V(R')|+(a+1)=|V(R)|+a$
, which is
$|S_1|+|S_2|\leq |V(R')|+(a+1)=|V(R)|+a$
, which is
![]() $t-1$
by (A2). To conclude the proof of (A5), we show that
$t-1$
by (A2). To conclude the proof of (A5), we show that
![]() $d_{K_s}(R)<d_{K_s}(R')$
if R does not satisfy (A5), contradicting the extremality of R.
$d_{K_s}(R)<d_{K_s}(R')$
if R does not satisfy (A5), contradicting the extremality of R.
Set
![]() $B'=(B_1-\{u,v\})\cup \{v'\}\subseteq V(R')$
and for each
$B'=(B_1-\{u,v\})\cup \{v'\}\subseteq V(R')$
and for each
![]() $0\leq m\leq s$
set
$0\leq m\leq s$
set
Recalling that
![]() $|B_1|=r\geq s \geq 3$
, we have
$|B_1|=r\geq s \geq 3$
, we have

For any
![]() $1\leq m\leq r-1$
, observe that
$1\leq m\leq r-1$
, observe that

with equality if and only if
![]() $m=1$
. Recalling that
$m=1$
. Recalling that
![]() $f_0=g_0=1$
, we conclude that
$f_0=g_0=1$
, we conclude that
![]() $f_m\leq g_m$
for all
$f_m\leq g_m$
for all
![]() $0\leq m\leq r-1$
with equality if and only if
$0\leq m\leq r-1$
with equality if and only if
![]() $m<2$
. If
$m<2$
. If
![]() $r\geq s+1$
, then this inequality holds for all
$r\geq s+1$
, then this inequality holds for all
![]() $2\leq m\leq s\leq r-1$
, and we conclude that
$2\leq m\leq s\leq r-1$
, and we conclude that

Now, suppose
![]() $r=s$
and
$r=s$
and
![]() $a\geq 2$
. We observe that
$a\geq 2$
. We observe that
![]() $h_1=\sum _{v\in V(R)-B_1}w(v)\geq |V(R)-B_1|p\geq p$
, so
$h_1=\sum _{v\in V(R)-B_1}w(v)\geq |V(R)-B_1|p\geq p$
, so

Once again, we conclude

Thus, if R does not satisfy (A5) then
![]() $d_{K_s}(R')>d_{K_s}(R)$
, contradicting the extremality of R. This completes the proof of Theorem 3.1.
$d_{K_s}(R')>d_{K_s}(R)$
, contradicting the extremality of R. This completes the proof of Theorem 3.1.
4 Eventual periodicity and counterexamples to Conjecture 1.2
In this section, we prove Theorem 1.3, providing conditions under which Conjecture 1.2 does and does not hold. Applying Theorem 2.4, we may reduce this to a problem about weighted graphs.
Say a weighted graph R admits a
![]() $(b,a)$
-partition if it has b vertices and satisfies the five conditions (A1)–(A5) of Theorem 3.1, with a being the number of parts in (A2). Theorem 1.4 shows that
$(b,a)$
-partition if it has b vertices and satisfies the five conditions (A1)–(A5) of Theorem 3.1, with a being the number of parts in (A2). Theorem 1.4 shows that
![]() $\varrho _s(K_t)$
is the maximum
$\varrho _s(K_t)$
is the maximum
![]() $K_s$
-density of a weighted graph R admitting a
$K_s$
-density of a weighted graph R admitting a
![]() $(b,a)$
-partition with
$(b,a)$
-partition with
![]() $a=t-1-b$
parts for some
$a=t-1-b$
parts for some
![]() $b<t$
; such R are inherently
$b<t$
; such R are inherently
![]() ${ \mathcal {K}}_t$
-free. From (A2), we have
${ \mathcal {K}}_t$
-free. From (A2), we have
![]() $b\geq s$
; additionally, because R cannot have fewer vertices than parts, we have
$b\geq s$
; additionally, because R cannot have fewer vertices than parts, we have
![]() $b\geq \lfloor t/2\rfloor $
. Conjecture 1.2 hypothesizes that the optimal density is attained when b matches one of these lower bounds.
$b\geq \lfloor t/2\rfloor $
. Conjecture 1.2 hypothesizes that the optimal density is attained when b matches one of these lower bounds.
Conjecture 4.1 (Conjecture 1.2, rephrased in terms of weighted graphs)
Fix integers
![]() $s,t$
with
$s,t$
with
![]() $3\leq s\leq t-2$
. The maximum
$3\leq s\leq t-2$
. The maximum
![]() $K_s$
-density of a weighted graph admitting a
$K_s$
-density of a weighted graph admitting a
![]() $(b,t-1-b)$
-partition is attained when
$(b,t-1-b)$
-partition is attained when
![]() $b=\max \{s,\lfloor t/2\rfloor \}$
.
$b=\max \{s,\lfloor t/2\rfloor \}$
.
For
![]() $t\geq 2s$
, Conjecture 4.1 hypothesizes that the extremal
$t\geq 2s$
, Conjecture 4.1 hypothesizes that the extremal
![]() ${ \mathcal {K}}_t$
-free weighted graphs follow an alternating pattern as depicted in Table 1. For odd t, the conjectural extremal construction is the complete balanced weighted graph
${ \mathcal {K}}_t$
-free weighted graphs follow an alternating pattern as depicted in Table 1. For odd t, the conjectural extremal construction is the complete balanced weighted graph
![]() $K_{\lfloor t/2\rfloor }^w$
, which has
$K_{\lfloor t/2\rfloor }^w$
, which has
![]() $b=\lfloor t/2\rfloor $
vertices with weight
$b=\lfloor t/2\rfloor $
vertices with weight
![]() $1/b$
each and has all
$1/b$
each and has all ![]() edge weights equal to 1. For even t, the conjectural extremal construction has
edge weights equal to 1. For even t, the conjectural extremal construction has
![]() $b=t/2$
vertices divided into one part of size 2 and
$b=t/2$
vertices divided into one part of size 2 and
![]() $b-2$
parts of size 1. That is, all edges have weight
$b-2$
parts of size 1. That is, all edges have weight
![]() $1$
except for one edge of weight
$1$
except for one edge of weight
![]() $1/2$
within the part of size 2.
$1/2$
within the part of size 2.
The proof of Theorem 1.3 is divided into three subsections. In Section 4.1, we show that Conjecture 4.1 holds if
![]() $t>s^2(s-1)/2 + s + 1$
, implying that the extremal constructions do eventually follow the aforementioned alternating pattern. In Section 4.2, we show that Conjecture 4.1 holds if
$t>s^2(s-1)/2 + s + 1$
, implying that the extremal constructions do eventually follow the aforementioned alternating pattern. In Section 4.2, we show that Conjecture 4.1 holds if
![]() $s=3,4$
or if
$s=3,4$
or if
![]() $t=s+2$
. Lastly, in Section 4.3, we provide counterexamples to Conjecture 4.1 for
$t=s+2$
. Lastly, in Section 4.3, we provide counterexamples to Conjecture 4.1 for
![]() $s=5$
as well as for any sufficiently large s.
$s=5$
as well as for any sufficiently large s.
4.1 Eventual Periodicity
We first show that Conjecture 4.1 holds when t is sufficiently large as a function of s.
Lemma 4.2. Fix integers
![]() $s,t$
with
$s,t$
with
![]() $3\leq s\leq t-2$
. Suppose R is a weighted graph admitting a
$3\leq s\leq t-2$
. Suppose R is a weighted graph admitting a
![]() $(b,a)$
-partition into
$(b,a)$
-partition into
![]() $B_1\cup \cdots \cup B_a$
for some
$B_1\cup \cdots \cup B_a$
for some
![]() $a,b$
satisfying
$a,b$
satisfying
![]() $a+b=t-1$
.
$a+b=t-1$
.
-
(1) Suppose t is odd with
 $t>s^2(s-1)/2$
. Set
$t>s^2(s-1)/2$
. Set
 $r=(t-1)/2$
and let
$r=(t-1)/2$
and let
 $K_r^w$
be the complete balanced weighted graph on r vertices. We have
$K_r^w$
be the complete balanced weighted graph on r vertices. We have
 $d_{K_s}(R)\leq d_{K_s}(K_r^w)$
with equality if and only if
$d_{K_s}(R)\leq d_{K_s}(K_r^w)$
with equality if and only if
 $R=K_r^w$
.
$R=K_r^w$
. -
(2) Suppose t is even with
 $t>s^2(s-1)/2+s$
. If
$t>s^2(s-1)/2+s$
. If
 $d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
then
$d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
then
 $a-1$
of the parts
$a-1$
of the parts
 $B_i$
must have cardinality 1, and the last part must have cardinality 2.
$B_i$
must have cardinality 1, and the last part must have cardinality 2.
Proof. We first prove (1). Suppose
![]() $t>s^2(s-1)/2$
is odd. Let
$t>s^2(s-1)/2$
is odd. Let
![]() $R_0$
be the weighted graph obtained from R by changing all edges weights of
$R_0$
be the weighted graph obtained from R by changing all edges weights of
![]() $1/2$
into 0 and let
$1/2$
into 0 and let
![]() $R_1$
be the weighted graph obtained from R by changing all edge weights of
$R_1$
be the weighted graph obtained from R by changing all edge weights of
![]() $1/2$
into 1. We claim that
$1/2$
into 1. We claim that
Indeed, if vertices
![]() $v_1,\ldots ,v_s\in V(R)$
induce
$v_1,\ldots ,v_s\in V(R)$
induce
![]() $m\geq 1$
edges of weight
$m\geq 1$
edges of weight
![]() $1/2$
in R, then the product of their edge weights is
$1/2$
in R, then the product of their edge weights is
![]() $\left (\frac 12\right )^m\leq \frac 12$
in R and is 1 in
$\left (\frac 12\right )^m\leq \frac 12$
in R and is 1 in
![]() $R_1$
.
$R_1$
.
We have ![]() . Write
. Write
![]() $w(B_i)=\sum _{v\in B_i}w(v)$
for the total weight of vertices in
$w(B_i)=\sum _{v\in B_i}w(v)$
for the total weight of vertices in
![]() $B_i$
. By Lemma 3.2, we have
$B_i$
. By Lemma 3.2, we have

Thus, setting ![]() , it suffices to show that
, it suffices to show that
![]() $\frac {f(a)+f(b)}2\leq f(\frac {a+b}2)=d_{K_s}(K_r^w)$
.
$\frac {f(a)+f(b)}2\leq f(\frac {a+b}2)=d_{K_s}(K_r^w)$
.
First, observe that

and that

It follows that
![]() $f"(x)<0$
when
$f"(x)<0$
when ![]() : for
: for
![]() $s=3$
, this can be checked manually, and for
$s=3$
, this can be checked manually, and for
![]() $s\geq 4$
, this follows from the inequality
$s\geq 4$
, this follows from the inequality

Hence, if ![]() , Jensen’s inequality implies
, Jensen’s inequality implies

with equality if and only if
![]() $a=b=r$
, (i.e.,
$a=b=r$
, (i.e.,
![]() $R=K_r^w$
). To see that
$R=K_r^w$
). To see that ![]() , note that (A5) implies
, note that (A5) implies
![]() $b\leq (s-1)a$
, yielding
$b\leq (s-1)a$
, yielding ![]() as desired.
as desired.
We now prove (2) using (1). Suppose
![]() $t>s^2(s-1)/2+s$
is even. Because
$t>s^2(s-1)/2+s$
is even. Because
![]() $t-1=a+b=\sum _{i=1}^a(|B_i|+1)$
is odd, there exists some k such that
$t-1=a+b=\sum _{i=1}^a(|B_i|+1)$
is odd, there exists some k such that
![]() $|B_k|+1$
is odd. Scaling
$|B_k|+1$
is odd. Scaling
![]() $R-B_k$
up by a factor of
$R-B_k$
up by a factor of
![]() $(1-w(B_k))^{-1}$
yields a weighted graph
$(1-w(B_k))^{-1}$
yields a weighted graph
![]() $R_0$
admitting a
$R_0$
admitting a
![]() $(b',a')$
-partition, where
$(b',a')$
-partition, where
![]() $a'=a-1$
and
$a'=a-1$
and
![]() $b'=b-|B_k|$
.
$b'=b-|B_k|$
.
Set
![]() $t'=a'+b'+1=t-|B_k|-1$
, which is odd, and set
$t'=a'+b'+1=t-|B_k|-1$
, which is odd, and set
![]() $r=(t'-1)/2$
. Let
$r=(t'-1)/2$
. Let
![]() $R'$
be the weighted graph obtained from R by replacing
$R'$
be the weighted graph obtained from R by replacing
![]() $V(R)-B_k$
with a set
$V(R)-B_k$
with a set
![]() $B'$
of r vertices of weight
$B'$
of r vertices of weight
![]() $(1-w(B_k))/r$
each, and setting
$(1-w(B_k))/r$
each, and setting
![]() $w(v',v)=1$
for each
$w(v',v)=1$
for each
![]() $v'\in B'$
and
$v'\in B'$
and
![]() $v\in V(R')\setminus \{v\}$
. That is,
$v\in V(R')\setminus \{v\}$
. That is,
![]() $R'[B']$
is a copy of
$R'[B']$
is a copy of
![]() $K_{r}^w$
scaled down by a factor of
$K_{r}^w$
scaled down by a factor of
![]() $1-w(B_k)$
. We note that
$1-w(B_k)$
. We note that
![]() $R'$
is
$R'$
is
![]() ${ \mathcal {K}}_t$
-free. Indeed, if
${ \mathcal {K}}_t$
-free. Indeed, if
![]() $(S_1,S_2)$
is a weighted clique in
$(S_1,S_2)$
is a weighted clique in
![]() $R'$
, then
$R'$
, then
![]() $S_2$
contains at most one vertex from
$S_2$
contains at most one vertex from
![]() $B_k$
, so
$B_k$
, so
![]() $|S_2|\leq r+1$
. Hence,
$|S_2|\leq r+1$
. Hence,
![]() $|S_1|+|S_2|\leq |V(R')|+r+1=|B_k|+2r+1=t-1$
.
$|S_1|+|S_2|\leq |V(R')|+r+1=|B_k|+2r+1=t-1$
.
Observe that
![]() $|B_k|\leq s-1$
by (A5), so
$|B_k|\leq s-1$
by (A5), so
![]() $t'>s^2(s-1)/2$
. By part (1), we have
$t'>s^2(s-1)/2$
. By part (1), we have
for all
![]() $m\leq s$
. Equality holds if and only if
$m\leq s$
. Equality holds if and only if
![]() $R_0=K_r^w$
, (i.e., if and only if
$R_0=K_r^w$
, (i.e., if and only if
![]() $|B_i|=1$
for each
$|B_i|=1$
for each
![]() $i\neq k$
). Hence, if
$i\neq k$
). Hence, if
![]() $|B_j|>1$
for some
$|B_j|>1$
for some
![]() $j\neq k$
, we have
$j\neq k$
, we have

contradicting the assumption that
![]() $d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
. To complete the proof of (2), we recall that
$d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
. To complete the proof of (2), we recall that
![]() $|B_k|$
is even and
$|B_k|$
is even and
![]() $|B_k|\leq |B_i|+1$
for any
$|B_k|\leq |B_i|+1$
for any
![]() $i\neq k$
by (A3). Hence, if
$i\neq k$
by (A3). Hence, if
![]() $|B_i|=1$
for all
$|B_i|=1$
for all
![]() $i\neq k$
then
$i\neq k$
then
![]() $|B_k|=2$
.
$|B_k|=2$
.
4.2 The Remaining Positive Results
We now prove Conjecture 4.1 in the remaining cases described in Theorem 1.3. We remark that the cases
![]() $t=s+2$
and
$t=s+2$
and
![]() $s=3$
were proven in [Reference Balogh, Liu and Sharifzadeh6]. However, the proofs of these cases are very straightforward when framed in terms of weighted graphs, so we present them for completeness.
$s=3$
were proven in [Reference Balogh, Liu and Sharifzadeh6]. However, the proofs of these cases are very straightforward when framed in terms of weighted graphs, so we present them for completeness.
Lemma 4.3. Fix
![]() $s\geq 3$
and let
$s\geq 3$
and let
![]() $t=s+2$
. If R is a
$t=s+2$
. If R is a
![]() ${ \mathcal {K}}_t$
-free weighted graph R with
${ \mathcal {K}}_t$
-free weighted graph R with
![]() $d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
of minimum cardinality, it admits an
$d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
of minimum cardinality, it admits an
![]() $(s,1)$
-partition.
$(s,1)$
-partition.
Proof. From Theorem 3.1(A2), R admits a
![]() $(b,a)$
partition for parameters
$(b,a)$
partition for parameters
![]() $a\geq 1$
and
$a\geq 1$
and
![]() $b\geq s$
satisfying
$b\geq s$
satisfying
![]() $a+b=t-1=s+1$
. It is immediate that
$a+b=t-1=s+1$
. It is immediate that
![]() $a=1$
and
$a=1$
and
![]() $b=s$
.
$b=s$
.
In the next two lemmas, we prove Conjecture 4.1 for
![]() $t\geq s+3$
and
$t\geq s+3$
and
![]() $s=3,4$
.
$s=3,4$
.
Lemma 4.4. Set
![]() $s=3$
and fix
$s=3$
and fix
![]() $t\geq s+3$
. Suppose R is a
$t\geq s+3$
. Suppose R is a
![]() ${ \mathcal {K}}_t$
-free weighted graph with
${ \mathcal {K}}_t$
-free weighted graph with
![]() $d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
of minimum cardinality. Then R admits a
$d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
of minimum cardinality. Then R admits a
![]() $(b,a)$
-partition with
$(b,a)$
-partition with
![]() $b=\max \{s,\lfloor t/2\rfloor \}$
.
$b=\max \{s,\lfloor t/2\rfloor \}$
.
Proof. By Theorem 3.1, R admits a
![]() $(b,a)$
-partition
$(b,a)$
-partition
![]() $B_1\cup \cdots \cup B_a$
such that
$B_1\cup \cdots \cup B_a$
such that
![]() $a+b=t-1$
. Moreover, combining (A5) with the inequality
$a+b=t-1$
. Moreover, combining (A5) with the inequality
![]() $t\geq 6$
, we conclude
$t\geq 6$
, we conclude
![]() $a\geq 2$
and
$a\geq 2$
and
![]() $|B_i|\leq 2$
for each i.
$|B_i|\leq 2$
for each i.
To show that
![]() $b=\lfloor t/2\rfloor =\max \{s,\lfloor t/2\rfloor \}$
when
$b=\lfloor t/2\rfloor =\max \{s,\lfloor t/2\rfloor \}$
when
![]() $t\geq 6$
, it suffices to show that all but at most one of the parts
$t\geq 6$
, it suffices to show that all but at most one of the parts
![]() $B_i$
have cardinality 1. Equivalently, we must show that R does not contain disjoint edges
$B_i$
have cardinality 1. Equivalently, we must show that R does not contain disjoint edges
![]() $uv$
and
$uv$
and
![]() $xy$
with
$xy$
with
![]() $w(u,v)=w(x,y)=1/2$
.
$w(u,v)=w(x,y)=1/2$
.
Suppose the contrary. We may assume without loss of generality that
![]() $d_{K_3}(R,\{x,y\})\geq d_{K_3}(R,\{u,v\})$
. Let
$d_{K_3}(R,\{x,y\})\geq d_{K_3}(R,\{u,v\})$
. Let
![]() $R'$
be the graph obtained from R by setting
$R'$
be the graph obtained from R by setting
![]() $w(u,v)=0$
and
$w(u,v)=0$
and
![]() $w(x,y)=1$
. We observe that
$w(x,y)=1$
. We observe that
![]() $d_{K_3}(R',\{x,y\})=2d_{K_3}(R,\{x,y\})$
and
$d_{K_3}(R',\{x,y\})=2d_{K_3}(R,\{x,y\})$
and
![]() $d_{K_3}(R',\{u,v\})=0$
, so
$d_{K_3}(R',\{u,v\})=0$
, so

Moreover,
![]() $R'$
is
$R'$
is
![]() ${ \mathcal {K}}_t$
-free, as the clique numbers of
${ \mathcal {K}}_t$
-free, as the clique numbers of
![]() $R^{\prime }_{>\frac 12}$
and
$R^{\prime }_{>\frac 12}$
and
![]() $R^{\prime }_{>0}$
satisfy
$R^{\prime }_{>0}$
satisfy
It follows that
![]() $R'$
is also an extremal
$R'$
is also an extremal
![]() ${ \mathcal {K}}_t$
-free weighted graph of minimal cardinality. However, this contradicts Theorem 3.1(A1), because
${ \mathcal {K}}_t$
-free weighted graph of minimal cardinality. However, this contradicts Theorem 3.1(A1), because
![]() $R'$
contains an edge of weight 0. We conclude that R cannot contain disjoint edges
$R'$
contains an edge of weight 0. We conclude that R cannot contain disjoint edges
![]() $uv$
and
$uv$
and
![]() $xy$
of weight
$xy$
of weight
![]() $1/2$
. This implies that all but at most one of the parts
$1/2$
. This implies that all but at most one of the parts
![]() $B_i$
have cardinality 1, which is equivalent to showing that
$B_i$
have cardinality 1, which is equivalent to showing that
![]() $b=\lfloor t/2\rfloor $
.
$b=\lfloor t/2\rfloor $
.
Lemma 4.5. Set
![]() $s=4$
and fix
$s=4$
and fix
![]() $t\geq s+3$
. Suppose R is a
$t\geq s+3$
. Suppose R is a
![]() ${ \mathcal {K}}_t$
-free weighted graph with
${ \mathcal {K}}_t$
-free weighted graph with
![]() $d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
of minimum cardinality. Then R admits a
$d_{K_s}(R)=\pi _s({ \mathcal {K}}_t)$
of minimum cardinality. Then R admits a
![]() $(b,a)$
-partition with
$(b,a)$
-partition with
![]() $b=\max \{s,\lfloor t/2\rfloor \}$
.
$b=\max \{s,\lfloor t/2\rfloor \}$
.
Proof. By Theorem 3.1, R admits a
![]() $(b,a)$
-partition
$(b,a)$
-partition
![]() $B_1\cup \cdots \cup B_a$
such that
$B_1\cup \cdots \cup B_a$
such that
![]() $a+b=t-1$
. Combining (A5) with the inequality
$a+b=t-1$
. Combining (A5) with the inequality
![]() $t\geq 7$
, we conclude that
$t\geq 7$
, we conclude that
![]() $a\geq 2$
and that each part has cardinality at most 3. If
$a\geq 2$
and that each part has cardinality at most 3. If
![]() $t=7$
, then we must have
$t=7$
, then we must have
![]() $a=2$
and
$a=2$
and
![]() $b=4$
, because (A2) implies
$b=4$
, because (A2) implies
![]() $b\geq 4$
. Henceforth, we assume
$b\geq 4$
. Henceforth, we assume
![]() $t\geq 8$
and show that
$t\geq 8$
and show that
![]() $b=\lfloor t/2\rfloor $
. Equivalently, we must show that at most one of the parts
$b=\lfloor t/2\rfloor $
. Equivalently, we must show that at most one of the parts
![]() $B_1,\ldots ,B_a$
has cardinality greater than 1.
$B_1,\ldots ,B_a$
has cardinality greater than 1.
Order the parts such that
![]() $3\geq |B_1|\geq |B_2|\geq \cdots \geq |B_a|\geq |B_1|-1$
; the last inequality is a consequence of (A3). Suppose for the sake of contradiction that
$3\geq |B_1|\geq |B_2|\geq \cdots \geq |B_a|\geq |B_1|-1$
; the last inequality is a consequence of (A3). Suppose for the sake of contradiction that
![]() $|B_2|\geq 2$
. We split our proof into three cases, based on
$|B_2|\geq 2$
. We split our proof into three cases, based on
![]() $|B_1|$
and
$|B_1|$
and
![]() $|B_2|$
. In each case, we derive a contradiction by constructing a
$|B_2|$
. In each case, we derive a contradiction by constructing a
![]() ${ \mathcal {K}}_t$
-free weighted graph with larger
${ \mathcal {K}}_t$
-free weighted graph with larger
![]() $K_s$
-density than R; these constructions are given in Figure 1.
$K_s$
-density than R; these constructions are given in Figure 1.

Figure 1 The optimizations in the proof of
![]() $s=4$
. Red edges have weight
$s=4$
. Red edges have weight
![]() $1/2$
and black edges have weight 1.
$1/2$
and black edges have weight 1.
Case 1:
![]() $|B_1|=|B_2|=3$
. In this case, the six vertices in
$|B_1|=|B_2|=3$
. In this case, the six vertices in
![]() $B_1$
and
$B_1$
and
![]() $B_2$
have the same weight p. Let
$B_2$
have the same weight p. Let
![]() $R_1$
be the weighted graph obtained from R by replacing
$R_1$
be the weighted graph obtained from R by replacing
![]() $B_1\cup B_2$
with a set
$B_1\cup B_2$
with a set
![]() $C=\{c_1,c_2,c_3,c_4\}$
of four vertices with weight
$C=\{c_1,c_2,c_3,c_4\}$
of four vertices with weight
![]() $3p/2$
each such that
$3p/2$
each such that
![]() $w(c_i,c_j)=w(c_i,v)=1$
for any
$w(c_i,c_j)=w(c_i,v)=1$
for any
![]() $i,j\in [4]$
and
$i,j\in [4]$
and
![]() $v\in B_3\cup \cdots \cup B_a$
. We note that
$v\in B_3\cup \cdots \cup B_a$
. We note that
![]() $(R_1)_{>\frac 12}$
and
$(R_1)_{>\frac 12}$
and
![]() $(R_1)_{>0}$
have clique numbers satisfying
$(R_1)_{>0}$
have clique numbers satisfying
so
![]() $R_1$
is
$R_1$
is
![]() ${ \mathcal {K}}_t$
-free. Additionally, one computes that
${ \mathcal {K}}_t$
-free. Additionally, one computes that

We conclude that

contradicting the extremality of R.
Case 2:
![]() $|B_1|=3$
and
$|B_1|=3$
and
![]() $|B_2|=2$
. Let p and q be the weights of vertices in
$|B_2|=2$
. Let p and q be the weights of vertices in
![]() $B_1$
and
$B_1$
and
![]() $B_2$
respectively; by (A4), we have
$B_2$
respectively; by (A4), we have
![]() $p\leq q$
. Let
$p\leq q$
. Let
![]() $R_2$
be the weighted graph obtained from R by replacing
$R_2$
be the weighted graph obtained from R by replacing
![]() $B_1$
with a set
$B_1$
with a set
![]() $C=\{c_1,c_2\}$
of two vertices with weight
$C=\{c_1,c_2\}$
of two vertices with weight
![]() $3p/2$
each such that
$3p/2$
each such that
![]() $w(c_1,c_2)=w(c_i,v)=1$
for any
$w(c_1,c_2)=w(c_i,v)=1$
for any
![]() $i\in [2]$
and
$i\in [2]$
and
![]() $v\in B_2\cup \cdots \cup B_a$
. We note that
$v\in B_2\cup \cdots \cup B_a$
. We note that
![]() $(R_2)_{>\frac 12}$
and
$(R_2)_{>\frac 12}$
and
![]() $(R_2)_{>0}$
have clique numbers satisfying
$(R_2)_{>0}$
have clique numbers satisfying
so
![]() $R_2$
is
$R_2$
is
![]() ${ \mathcal {K}}_t$
-free. One computes that
${ \mathcal {K}}_t$
-free. One computes that

We now claim that

is positive for
![]() $2\leq m\leq 4$
. This is immediate for
$2\leq m\leq 4$
. This is immediate for
![]() $m=2$
. For
$m=2$
. For
![]() $m=3,4$
, only the
$m=3,4$
, only the
![]() $r=3$
term is negative, and one may check that the sum of the
$r=3$
term is negative, and one may check that the sum of the
![]() $r=2$
and
$r=2$
and
![]() $r=3$
terms is positive via the relations
$r=3$
terms is positive via the relations
and
![]() $d_{K_0}(R[B_2])\leq \frac 2p d_{K_1}(R[B_2])\leq \left (\frac 2p\right )^2d_{K_2}(R[B_2])$
. Thus,
$d_{K_0}(R[B_2])\leq \frac 2p d_{K_1}(R[B_2])\leq \left (\frac 2p\right )^2d_{K_2}(R[B_2])$
. Thus,
![]() $d_{K_m}(R_2[C\cup B_2])>d_{K_m}(R[B_1\cup B_2])$
for
$d_{K_m}(R_2[C\cup B_2])>d_{K_m}(R[B_1\cup B_2])$
for
![]() $2\leq m \leq 4$
. It follows that
$2\leq m \leq 4$
. It follows that

contradicting the extremality of R.
Case 3:
![]() $|B_1|=|B_2|=2$
. In this case, the four vertices in
$|B_1|=|B_2|=2$
. In this case, the four vertices in
![]() $B_1$
and
$B_1$
and
![]() $B_2$
have the same weight p. Moreover, we have
$B_2$
have the same weight p. Moreover, we have
![]() $a\geq 3$
because
$a\geq 3$
because
![]() $t\geq 8$
. Let
$t\geq 8$
. Let
![]() $R_3$
be the weighted graph obtained from R by replacing
$R_3$
be the weighted graph obtained from R by replacing
![]() $B_1\cup B_2$
with a set
$B_1\cup B_2$
with a set
![]() $C=\{c_1,c_2,c_3\}$
of three vertices with weight
$C=\{c_1,c_2,c_3\}$
of three vertices with weight
![]() $4p/3$
each such that
$4p/3$
each such that
![]() $w(c_i,c_j)=w(c_i,v)=1$
for any
$w(c_i,c_j)=w(c_i,v)=1$
for any
![]() $i,j\in [3]$
and
$i,j\in [3]$
and
![]() $v\in B_3\cup \cdots \cup B_a$
. We note that
$v\in B_3\cup \cdots \cup B_a$
. We note that
![]() $(R_3)_{>\frac 12}$
and
$(R_3)_{>\frac 12}$
and
![]() $(R_3)_{>0}$
have clique numbers satisfying
$(R_3)_{>0}$
have clique numbers satisfying
so
![]() $R_3$
is
$R_3$
is
![]() ${ \mathcal {K}}_t$
-free. One computes that
${ \mathcal {K}}_t$
-free. One computes that

We now claim that

is positive for
![]() $2\leq m\leq 4$
. This is immediate for
$2\leq m\leq 4$
. This is immediate for
![]() $m=2,3$
. For
$m=2,3$
. For
![]() $m=4$
, only the
$m=4$
, only the
![]() $r=4$
term is negative. By (A4), we have
$r=4$
term is negative. By (A4), we have
![]() $d_{K_1}(R[B_3])=\sum _{v\in B_3}w(v)\geq p$
, so
$d_{K_1}(R[B_3])=\sum _{v\in B_3}w(v)\geq p$
, so

and thus
![]() $d_{K_m}(R_3[C\cup B_3])>d_{K_m}(R[B_1\cup B_2\cup B_3])$
for
$d_{K_m}(R_3[C\cup B_3])>d_{K_m}(R[B_1\cup B_2\cup B_3])$
for
![]() $2\leq m \leq 4$
. Therefore, setting
$2\leq m \leq 4$
. Therefore, setting
![]() $B=B_1\cup B_2\cup B_3$
, we have
$B=B_1\cup B_2\cup B_3$
, we have

contradicting the extremality of R.
4.3 Counterexamples to Conjecture 1.2
We conclude this section by presenting some counterexamples to Conjecture 1.2 when t is slightly larger than
![]() $2s$
. We begin with two counterexamples in the
$2s$
. We begin with two counterexamples in the
![]() $s=5$
case, then use the same ideas to derive a family of counterexamples for all sufficiently large s and any t with
$s=5$
case, then use the same ideas to derive a family of counterexamples for all sufficiently large s and any t with
![]() $2s\leq t\leq 2.08s$
.
$2s\leq t\leq 2.08s$
.
We first observe that Conjecture 1.2 is not true for
![]() $s=5$
and
$s=5$
and
![]() $t\in \{10,11\}$
, via the counterexamples pictured in Figure 2.
$t\in \{10,11\}$
, via the counterexamples pictured in Figure 2.
For the case
![]() $s=5$
and
$s=5$
and
![]() $t=10$
, Conjecture 1.2 hypothesizes that
$t=10$
, Conjecture 1.2 hypothesizes that
![]() $\pi _s({ \mathcal {K}}_t)$
is attained by a weighted graph
$\pi _s({ \mathcal {K}}_t)$
is attained by a weighted graph
![]() $R_1$
of order 5 with exactly one edge of weight
$R_1$
of order 5 with exactly one edge of weight
![]() $1/2$
, such that the two vertices incident to the edge of weight
$1/2$
, such that the two vertices incident to the edge of weight
![]() $1/2$
have the same weight p and the remaining three vertices have the same weight q. Let
$1/2$
have the same weight p and the remaining three vertices have the same weight q. Let
![]() $R_2$
be a weighted graph of order 6 in which every vertex has weight
$R_2$
be a weighted graph of order 6 in which every vertex has weight
![]() $1/6$
, three disjoint edges have weight
$1/6$
, three disjoint edges have weight
![]() $1/2$
, and all remaining edges have weight 1. It is straightforward to check that
$1/2$
, and all remaining edges have weight 1. It is straightforward to check that
![]() $R_2$
is
$R_2$
is
![]() ${ \mathcal {K}}_{10}$
-free and that
${ \mathcal {K}}_{10}$
-free and that

Thus Conjecture 1.2 is not true in the case
![]() $s=5$
,
$s=5$
,
![]() $t=10$
.
$t=10$
.

Figure 2 Counterexamples to Conjecture 1.2 for
![]() $s=5$
and
$s=5$
and
![]() $t\in \{10,11\}$
. Red edges have weight
$t\in \{10,11\}$
. Red edges have weight
![]() $1/2$
and black edges have weight 1.
$1/2$
and black edges have weight 1.
For the case
![]() $s=5$
and
$s=5$
and
![]() $t=11$
, Conjecture 1.2 hypothesizes that
$t=11$
, Conjecture 1.2 hypothesizes that
![]() $\pi _s({ \mathcal {K}}_t)$
is attained by the complete balanced weighted graph
$\pi _s({ \mathcal {K}}_t)$
is attained by the complete balanced weighted graph
![]() $K_5^w$
, which has 5 vertices of weight
$K_5^w$
, which has 5 vertices of weight
![]() $1/5$
each and has all edge weights equal to 1. Let
$1/5$
each and has all edge weights equal to 1. Let
![]() $R'$
be a weighted graph of order 6 with two disjoint edges of weight
$R'$
be a weighted graph of order 6 with two disjoint edges of weight
![]() $1/2$
and all other edge weights equal to 1, such that the four vertices incident to the weight-
$1/2$
and all other edge weights equal to 1, such that the four vertices incident to the weight-
![]() $1/2$
edges have weight p and the remaining two vertices have weight q. It is straightforward to check that
$1/2$
edges have weight p and the remaining two vertices have weight q. It is straightforward to check that
![]() $R'$
is
$R'$
is
![]() ${ \mathcal {K}}_{11}$
-free. Moreover, if the parameters
${ \mathcal {K}}_{11}$
-free. Moreover, if the parameters
![]() $p,q$
are optimized, we have
$p,q$
are optimized, we have

Notably, the inequality holds with
![]() $p=0.16$
and
$p=0.16$
and
![]() $q=0.18$
. Thus Conjecture 1.2 is also false in the case
$q=0.18$
. Thus Conjecture 1.2 is also false in the case
![]() $s=5$
,
$s=5$
,
![]() $t=11$
.
$t=11$
.
We now show that a similar construction works if s is sufficiently large.
Lemma 4.6. Conjecture 1.2 is false for all sufficiently large s and any t satisfying
![]() $2s\leq t\leq 2.08s$
.
$2s\leq t\leq 2.08s$
.
Proof. First suppose t is odd (i.e.,
![]() $t=2r+1$
for some integer
$t=2r+1$
for some integer
![]() $r\geq s$
). Conjecture 1.2 hypothesizes that
$r\geq s$
). Conjecture 1.2 hypothesizes that
![]() $\pi _s({ \mathcal {K}}_t)$
is attained by the complete balanced weighted graph
$\pi _s({ \mathcal {K}}_t)$
is attained by the complete balanced weighted graph
![]() $K_r^w$
, which has r vertices of weight
$K_r^w$
, which has r vertices of weight
![]() $1/r$
each and has all edge weights equal to 1. Let
$1/r$
each and has all edge weights equal to 1. Let
![]() $R'$
be a weighted graph on
$R'$
be a weighted graph on
![]() $(r+1)$
vertices with two disjoint edges of weight
$(r+1)$
vertices with two disjoint edges of weight
![]() $1/2$
and all other edge weights equal to 1, such that the four vertices incident to weight-
$1/2$
and all other edge weights equal to 1, such that the four vertices incident to weight-
![]() $1/2$
edges have weight
$1/2$
edges have weight
![]() $3/4r$
and the remaining
$3/4r$
and the remaining
![]() $r-3$
vertices have weight
$r-3$
vertices have weight
![]() $1/r$
. It is straightforward to check that
$1/r$
. It is straightforward to check that
![]() $R'$
is
$R'$
is
![]() ${ \mathcal {K}}_t$
-free. Moreover, because
${ \mathcal {K}}_t$
-free. Moreover, because
![]() $s\leq r\leq 1.04s$
, we have
$s\leq r\leq 1.04s$
, we have

if
![]() $s\leq r$
is sufficiently large.
$s\leq r$
is sufficiently large.
Next, suppose t is even (i.e.,
![]() $t=2r$
for some integer
$t=2r$
for some integer
![]() $r\geq s$
). Conjecture 1.2 hypothesizes that
$r\geq s$
). Conjecture 1.2 hypothesizes that
![]() $\pi _s({ \mathcal {K}}_t)$
is attained by a weighted graph
$\pi _s({ \mathcal {K}}_t)$
is attained by a weighted graph
![]() $R_1$
on r vertices with exactly one edge of weight
$R_1$
on r vertices with exactly one edge of weight
![]() $1/2$
. By Lemma 3.2, we have that
$1/2$
. By Lemma 3.2, we have that

Let
![]() $R_2$
be a weighted graph on
$R_2$
be a weighted graph on
![]() $(r+1)$
vertices with three disjoint edges of weight
$(r+1)$
vertices with three disjoint edges of weight
![]() $1/2$
and all other edge weights equal to 1, such that the six vertices incident to weight-1/2 edges have weight
$1/2$
and all other edge weights equal to 1, such that the six vertices incident to weight-1/2 edges have weight
![]() $5/6r$
and the remaining
$5/6r$
and the remaining
![]() $r-5$
vertices have weight
$r-5$
vertices have weight
![]() $1/r$
. It is straightforward to check that
$1/r$
. It is straightforward to check that
![]() $R_2$
is
$R_2$
is
![]() ${ \mathcal {K}}_t$
-free. Moreover, because
${ \mathcal {K}}_t$
-free. Moreover, because
![]() $s\leq r\leq 1.04s$
, we have
$s\leq r\leq 1.04s$
, we have

if
![]() $s\leq r$
is sufficiently large.
$s\leq r$
is sufficiently large.
5 Concluding Remarks
In this paper, we combinatorially resolve the generalized Ramsey–Turán problem for cliques, reducing its determination to a bounded optimization problem about finding the optimal
![]() $(b,a)$
-partition, which remains an intriguing problem.
$(b,a)$
-partition, which remains an intriguing problem.
Problem 5.1. Given integers
![]() $t-2\geq s\ge 3$
, which
$t-2\geq s\ge 3$
, which
![]() $(b,a)$
-partition with
$(b,a)$
-partition with
![]() $a+b=t-1$
achieves the Ramsey–Turán density
$a+b=t-1$
achieves the Ramsey–Turán density
![]() $\varrho _s(K_t)$
?
$\varrho _s(K_t)$
?
An easier, yet still interesting, problem is the following. By Theorem 1.3, the threshold value of t for the extremal periodic behavior lies somewhere between
![]() $2.08s$
and
$2.08s$
and
![]() $s^3$
. Which bound is closer to the truth?
$s^3$
. Which bound is closer to the truth?
For general graphs, an Erdős–Stone–Simonovits type result is still out of reach. For example, we do not know whether
![]() $\varrho _2(K_{2,2,2})>0$
[Reference Erdős, Hajnal, Sós and Szemerédi16, Reference Simonovits and Sós33]. In light of this, we wonder the following.
$\varrho _2(K_{2,2,2})>0$
[Reference Erdős, Hajnal, Sós and Szemerédi16, Reference Simonovits and Sós33]. In light of this, we wonder the following.
Problem 5.2. Decide if
![]() $\varrho _3(K_{2,2,2,2})>0$
or not.
$\varrho _3(K_{2,2,2,2})>0$
or not.
Another natural future direction is to study
![]() $\mathrm {RT}(n,K_s,K_t,f(n))$
for smaller independence numbers (e.g., when
$\mathrm {RT}(n,K_s,K_t,f(n))$
for smaller independence numbers (e.g., when
![]() $f(n)=n^{1-\varepsilon }$
or when it is the inverse function of the Ramsey function, say
$f(n)=n^{1-\varepsilon }$
or when it is the inverse function of the Ramsey function, say
![]() $f(n)=\sqrt {n\log n}$
).
$f(n)=\sqrt {n\log n}$
).
Note. After this paper was written, we learned that Balogh, Magnan and Palmer [Reference Balogh, Magnan and Palmer7] independently proved some related results.
Acknowledgments
We would like to thank the anonymous referee for their useful comments and suggestions.
Competing interest
The authors have no competing interests to declare.
Financial support
The research of J. Gao and H. Liu was supported by IBS-R029-C4. The research of S. Jiang was supported by Hubei Provincial Natural Science Foundation of China (No. 2025AFB666), National Natural Science Foundation of China (No. 11901246), China Scholarship Council and IBS-R029-C4. The research of M. Sankar was supported by NSF GRFP Grant DGE-1656518 and a Hertz Fellowship.