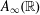Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-30T10:47:04.922Z Has data issue: false hasContentIssue false
  • English
  • Français

FLOW WITH $A_{\infty }(\mathbb{R})$ DENSITY AND TRANSPORT EQUATION IN 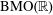$\text{BMO}(\mathbb{R})$

Part of: Harmonic analysis in several variables General theory in ordinary differential equations

Published online by Cambridge University Press:  29 November 2019

RENJIN JIANG ,
KANGWEI LI  and
JIE XIAO
RENJIN JIANG
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin, China; [email protected], [email protected]
KANGWEI LI
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin, China; [email protected], [email protected] Basque Center for Applied Mathematics, Alameda de Mazarredo 14, Bilbao, Spain
JIE XIAO
Affiliation:
Department of Math and Stat, Memorial University, St. John’s, NLA1C 5S7, Canada; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that, if 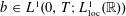$b\in L^{1}(0,T;L_{\operatorname{loc}}^{1}(\mathbb{R}))$ has a spatial derivative in the John–Nirenberg space 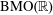$\operatorname{BMO}(\mathbb{R})$, then it generates a unique flow 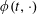$\unicode[STIX]{x1D719}(t,\cdot )$ which has an 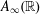$A_{\infty }(\mathbb{R})$ density for each time 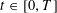$t\in [0,T]$. Our condition on the map 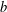$b$ is not only optimal but also produces a sharp quantitative estimate for the density. As a killer application we achieve the well-posedness for a Cauchy problem of the transport equation in 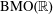$\operatorname{BMO}(\mathbb{R})$.

MSC classification

Primary: 42B37: Harmonic analysis and PDE
Secondary: 34A12: Initial value problems, existence, uniqueness, continuous dependence and continuation of solutions
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e43
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Alberico, T., Corporente, R. and Sbordone, C., ‘Explicit bounds for composition operators preserving BMO(ℝ)’, Georgian Math. J. 14 (2007), 21–32.Google Scholar
Ambrosio, L., ‘Transport equation and Cauchy problem for BV vector fields’, Invent. Math. 158 (2004), 227–260.Google Scholar
Beurling, A. and Ahlfors, L., ‘The boundary correspondence under quasiconformal mappings’, Acta Math. 96 (1956), 125–142.Google Scholar
Bloom, S., ‘Sharp weights and BMO-preserving homeomorphisms’, Stud. Math. 96 (1990), 1–10.Google Scholar
Bonk, M., Heinonen, J. and Saksman, E., ‘Logarithmic potentials, quasiconformal flows, and Q-curvature’, Duke Math. J. 142 (2008), 197–239.Google Scholar
Bouchut, F. and James, F., ‘Duality solutions for pressureless gases, monotone scalar conservation laws, and uniqueness’, Comm. Partial Differential Equations 24 (1999), 2173–2189.Google Scholar
Chung, D., Pereyra, C. and Pérez, C., ‘Sharp bounds for general commutators on weighted Lebesgue spaces’, Trans. Amer. Math. Soc. 364 (2012), 1163–1177.Google Scholar
Clop, A., Jiang, R., Mateu, J. and Orobitg, J., ‘Linear transport equations for vector fields with subexponentially integrable divergence’, Calc. Var. Partial Differential Equations 55 (2016), Art. 21, 30 pp.Google Scholar
Clop, A., Jiang, R., Mateu, J. and Orobitg, J., ‘Flows for non-smooth vector fields with sub-exponentially integrable divergence’, J. Differential Equations 261 (2016), 1237–1263.Google Scholar
Clop, A., Jiang, R., Mateu, J. and Orobitg, J., ‘A note on transport equations in quasiconformally invariant spaces’, Adv. Calc. Var. 11 (2018), 193–202.Google Scholar
Clop, A., Jylhä, H., Mateu, J. and Orobitg, J., ‘Well-posedness for the continuity equation for vector fields with suitable modulus of continuity’, J. Funct. Anal. 276 (2019), 45–77.Google Scholar
Crippa, G. and De Lellis, C., ‘Estimates and regularity results for the DiPerna-Lions flow’, J. Reine Angew. Math. 616 (2008), 15–46.Google Scholar
DiPerna, R. J. and Lions, P. L., ‘Ordinary differential equations, transport theory and Sobolev spaces’, Invent. Math. 98 (1989), 511–547.Google Scholar
Donaire, J. J., Llorente, J. G. and Nicolau, A., ‘Differentiability of functions in the Zygmund class’, Proc. Lond. Math. Soc. (3) 108 (2014), 133–158.Google Scholar
Fan, Y., Hu, Y. and Shen, Y., ‘A note on BMO map induced by strongly quasisymmetric homeomorphism’, Proc. Amer. Math. Soc. 145 (2017), 2505–2512.Google Scholar
Fefferman, C. and Stein, E. M., ‘ H p spaces of several variables’, Acta Math. 129 (1972), 137–193.Google Scholar
Fominykh, M. A., ‘Admissible changes of variables in the class of BMO functions’, Math. Notes 43 (1988), 366–371.Google Scholar
Grafakos, L., Modern Fourier Analysis, 2nd edn, Graduate Texts in Mathematics, 250 (Springer, New York, 2009), xvi+504pp.Google Scholar
Hytönen, T. and Pérez, C., ‘Sharp weighted bounds involving A ∞ ’, Anal. PDE 6 (2013), 777–818.Google Scholar
Johnson, R. and Neugebauer, C. J., ‘Homeomorphisms preserving A p(ℝ)’, Rev. Mat. Iberoa. 3 (1987), 249–273.Google Scholar
Jones, P., ‘Homeomorphisms of the line which preserve BMO’, Ark. Mat. 21 (1983), 229–231.Google Scholar
Koch, H., Koskela, P., Saksman, E. and Soto, T., ‘Bounded compositions on scaling invariant Besov spaces’, J. Funct. Anal. 266 (2014), 2765–2788.Google Scholar
Koskela, P., Yang, D. and Zhou, Y., ‘Pointwise characterizations of Besov and Triebel–Lizorkin spaces and quasiconformal mappings’, Adv. Math. 226 (2011), 3579–3621.Google Scholar
Li, K., Ombrosi, S. and Pérez, C., ‘Proof of an extension of E. Sawyer’s conjecture about weighted mixed weak-type estimates’, Math. Ann. 374 (2019), 907–929.Google Scholar
Mucha, P. B., ‘Transport equation: extension of classical results for divb ∈ BMO’, J. Differential Equations 249 (2010), 1871–1883.Google Scholar
Reimann, H. M., ‘Functions of bounded mean oscillation and quasiconformal mappings’, Comment. Math. Helv. 49 (1974), 260–276.Google Scholar
Reimann, H. M., ‘Ordinary differential equations and quasiconformal mappings’, Invent. Math. 33 (1976), 247–270.Google Scholar
Vodop’yanov, S.K., ‘Mappings of homogeneous groups and imbeddings of functional spaces’, Sib. Math. Zh. 30 (1989), 25–41.Google Scholar
Xiao, J., ‘The transport equation in scaling invariant Besov or Essén–Janson–Peng–Xiao space’, J. Differential Equations 266 (2019), 7124–7151.Google Scholar
Yang, D., Yuan, W. and Zhou, Y., ‘Sharp boundedness of quasiconformal composition operators on Triebel–Lizorkin type spaces’, J. Geom. Anal. 27 (2017), 1548–1588.Google Scholar