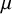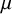1 Introduction
Let p be a prime number. Let G be a smooth affine group scheme over the ring of p-adic integers
![]() ${\mathbb Z}_p$
. Let
${\mathbb Z}_p$
. Let
![]() $ \mu \colon {\mathbb G}_m \to G_{W(k)}:=G \times _{\mathrm {Spec} {\mathbb Z}_p} \mathrm {Spec} W(k) $
be a cocharacter defined over
$ \mu \colon {\mathbb G}_m \to G_{W(k)}:=G \times _{\mathrm {Spec} {\mathbb Z}_p} \mathrm {Spec} W(k) $
be a cocharacter defined over
![]() $W(k)$
, where k is a perfect field of characteristic p and
$W(k)$
, where k is a perfect field of characteristic p and
![]() $W(k)$
is the ring of p-typical Witt vectors of k. The theory of G-
$W(k)$
is the ring of p-typical Witt vectors of k. The theory of G-
![]() $\mu $
-displays was originally introduced by Bültel [Reference BültelBül08] and Bültel–Pappas [Reference Bültel and PappasBP20] to study integral models of Shimura varieties and Rapoport–Zink spaces. In [Reference ItoIto23], we studied the notion of G-
$\mu $
-displays was originally introduced by Bültel [Reference BültelBül08] and Bültel–Pappas [Reference Bültel and PappasBP20] to study integral models of Shimura varieties and Rapoport–Zink spaces. In [Reference ItoIto23], we studied the notion of G-
![]() $\mu $
-displays over the prismatic site of Bhatt–Scholze [Reference Bhatt and ScholzeBS22]. The purpose of this paper is to develop the deformation theory for G-
$\mu $
-displays over the prismatic site of Bhatt–Scholze [Reference Bhatt and ScholzeBS22]. The purpose of this paper is to develop the deformation theory for G-
![]() $\mu $
-displays over the prismatic site, which has applications in the theory of integral models of Shimura varieties and local Shimura varieties. Our deformation theory for
$\mu $
-displays over the prismatic site, which has applications in the theory of integral models of Shimura varieties and local Shimura varieties. Our deformation theory for
![]() $G= {\mathrm {GL}} _N$
provides new perspectives on some classification results of p-divisible groups. We also discuss how our results can be interpreted in terms of prismatic F-gauges introduced by Drinfeld and Bhatt–Lurie.
$G= {\mathrm {GL}} _N$
provides new perspectives on some classification results of p-divisible groups. We also discuss how our results can be interpreted in terms of prismatic F-gauges introduced by Drinfeld and Bhatt–Lurie.
1.1 Main results
Let
![]() $(A, I)$
be a bounded prism in the sense of [Reference Bhatt and ScholzeBS22], such that A is a
$(A, I)$
be a bounded prism in the sense of [Reference Bhatt and ScholzeBS22], such that A is a
![]() $W(k)$
-algebra. We study the groupoid of G-
$W(k)$
-algebra. We study the groupoid of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
$(A, I)$
which is introduced in [Reference ItoIto23] following the theory of G-
![]() $\mu $
-displays over higher frames developed by Lau [Reference LauLau21] and the work of Bartling [Reference BartlingBar22]. The groupoid
$\mu $
-displays over higher frames developed by Lau [Reference LauLau21] and the work of Bartling [Reference BartlingBar22]. The groupoid ![]() is equivalent to the groupoid of G-Breuil–Kisin modules of type
is equivalent to the groupoid of G-Breuil–Kisin modules of type
![]() $\mu $
over
$\mu $
over
![]() $(A, I)$
, which may be more familiar to the reader. See Section 2.4 for details.
$(A, I)$
, which may be more familiar to the reader. See Section 2.4 for details.
Let us summarize the main results of this paper. In the remainder of this introduction, we assume that
![]() $\mu $
is 1-bounded; that is, the weights of the action of
$\mu $
is 1-bounded; that is, the weights of the action of
![]() ${\mathbb G}_m$
on the Lie algebra of
${\mathbb G}_m$
on the Lie algebra of
![]() $G_{W(k)}$
induced by
$G_{W(k)}$
induced by
![]() $g \mapsto \mu (t)^{-1}g\mu (t)$
are
$g \mapsto \mu (t)^{-1}g\mu (t)$
are
![]() $\leq 1$
([Reference LauLau21, Definition 6.3.1]). If G is reductive, then
$\leq 1$
([Reference LauLau21, Definition 6.3.1]). If G is reductive, then
![]() $\mu $
is 1-bounded if and only if
$\mu $
is 1-bounded if and only if
![]() $\mu $
is minuscule.
$\mu $
is minuscule.
Definition 1.1.1. For a p-adically complete ring R over
![]() $W(k)$
, the groupoid of prismatic G-
$W(k)$
, the groupoid of prismatic G-
![]() $\mu $
-displays over R is defined to be
$\mu $
-displays over R is defined to be
Here, ![]() is the absolute prismatic site of R, whose objects are the bounded prisms
is the absolute prismatic site of R, whose objects are the bounded prisms
![]() $(A, I)$
equipped with a homomorphism
$(A, I)$
equipped with a homomorphism
![]() $g \colon R \to A/I$
. For a prismatic G-
$g \colon R \to A/I$
. For a prismatic G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}$
over R and an object
$\mathfrak {Q}$
over R and an object ![]() , the image of
, the image of
![]() $\mathfrak {Q}$
in
$\mathfrak {Q}$
in ![]() is denoted by
is denoted by
![]() $\mathfrak {Q}_{(A, I)}$
or
$\mathfrak {Q}_{(A, I)}$
or
![]() $\mathfrak {Q}_{g}$
.
$\mathfrak {Q}_{g}$
.
Let
![]() $\mathcal {C}_{W(k)}$
be the category of complete regular local rings R over
$\mathcal {C}_{W(k)}$
be the category of complete regular local rings R over
![]() $W(k)$
with residue field k. Let
$W(k)$
with residue field k. Let
![]() $R \in \mathcal {C}_{W(k)}$
. The prism
$R \in \mathcal {C}_{W(k)}$
. The prism
![]() $(W(k), (p))$
with the natural homomorphism
$(W(k), (p))$
with the natural homomorphism
![]() $R \to k$
is an object of
$R \to k$
is an object of ![]() , which we consider as ‘the base point’. Let
, which we consider as ‘the base point’. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(W(k), (p))$
(or equivalently, a prismatic G-
$(W(k), (p))$
(or equivalently, a prismatic G-
![]() $\mu $
-display over k).
$\mu $
-display over k).
Definition 1.1.2. A deformation of
![]() $\mathcal {Q}$
over R is a prismatic G-
$\mathcal {Q}$
over R is a prismatic G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}$
over R together with an isomorphism
$\mathfrak {Q}$
over R together with an isomorphism
![]() $\mathfrak {Q}_{(W(k), (p))} \overset {\sim }{\to } \mathcal {Q}$
of G-
$\mathfrak {Q}_{(W(k), (p))} \overset {\sim }{\to } \mathcal {Q}$
of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(W(k), (p))$
. We say that
$(W(k), (p))$
. We say that
![]() $\mathfrak {Q}$
is a universal deformation of
$\mathfrak {Q}$
is a universal deformation of
![]() $\mathcal {Q}$
if, for any
$\mathcal {Q}$
if, for any
![]() $R' \in \mathcal {C}_{W(k)}$
and any deformation
$R' \in \mathcal {C}_{W(k)}$
and any deformation
![]() $\mathfrak {Q}'$
of
$\mathfrak {Q}'$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R'$
, there exists a unique local homomorphism
$R'$
, there exists a unique local homomorphism
![]() $ h \colon R \to R' $
over
$ h \colon R \to R' $
over
![]() $W(k)$
such that the base change of
$W(k)$
such that the base change of
![]() $\mathfrak {Q}$
along h is isomorphic to
$\mathfrak {Q}$
along h is isomorphic to
![]() $\mathfrak {Q}'$
as a deformation of
$\mathfrak {Q}'$
as a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R'$
.
$R'$
.
Our first main result concerns the existence of a universal deformation of
![]() $\mathcal {Q}$
. Let
$\mathcal {Q}$
. Let
![]() $U^{-}_{\mu } \subset G_{W(k)}$
be the closed subgroup scheme consisting of elements
$U^{-}_{\mu } \subset G_{W(k)}$
be the closed subgroup scheme consisting of elements
![]() $g \in G_{W(k)}$
such that
$g \in G_{W(k)}$
such that
![]() $\lim _{t \to 0} \mu (t)^{-1}g\mu (t)=1$
. Let
$\lim _{t \to 0} \mu (t)^{-1}g\mu (t)=1$
. Let
![]() $R_{G, \mu }$
be the completed local ring of
$R_{G, \mu }$
be the completed local ring of
![]() $U^{-}_{\mu }$
at the identity element
$U^{-}_{\mu }$
at the identity element
![]() $1 \in U^{-}_{\mu }$
. Since
$1 \in U^{-}_{\mu }$
. Since
![]() $U^{-}_{\mu }$
is smooth, there exists an isomorphism over
$U^{-}_{\mu }$
is smooth, there exists an isomorphism over
![]() $W(k)$
$W(k)$
and in particular,
![]() $R_{G, \mu } \in \mathcal {C}_{W(k)}$
.
$R_{G, \mu } \in \mathcal {C}_{W(k)}$
.
Theorem 1.1.3 (Theorem 4.1.7).
Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(W(k), (p))$
. There exists a universal deformation
$(W(k), (p))$
. There exists a universal deformation
![]() $\mathfrak {Q}^{\mathrm {univ}}$
of
$\mathfrak {Q}^{\mathrm {univ}}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
.
$R_{G, \mu }$
.
We will show that
![]() $\mathfrak {Q}^{\mathrm {univ}}$
possesses a similar universal property for a larger class of deformations of
$\mathfrak {Q}^{\mathrm {univ}}$
possesses a similar universal property for a larger class of deformations of
![]() $\mathcal {Q}$
. To explain this, we need to introduce some notation.
$\mathcal {Q}$
. To explain this, we need to introduce some notation.
We consider a prism of Breuil–Kisin type
where
![]() $\mathcal {E} \in W(k)[[t_1, \dotsc , t_n]]$
is a formal power series whose constant term is p and the Frobenius
$\mathcal {E} \in W(k)[[t_1, \dotsc , t_n]]$
is a formal power series whose constant term is p and the Frobenius
![]() $\phi $
of
$\phi $
of
![]() $W(k)[[t_1, \dotsc , t_n]]$
is such that
$W(k)[[t_1, \dotsc , t_n]]$
is such that
![]() $\phi (t_i)=t^p_i$
for
$\phi (t_i)=t^p_i$
for
![]() $1 \leq i \leq n$
. Here, n could be any nonnegative integer. We set
$1 \leq i \leq n$
. Here, n could be any nonnegative integer. We set
![]() $ R:=\mathfrak {S}/\mathcal {E}, $
which belongs to the category
$ R:=\mathfrak {S}/\mathcal {E}, $
which belongs to the category
![]() $\mathcal {C}_{W(k)}$
.
$\mathcal {C}_{W(k)}$
.
The following fact plays a crucial role in our work.
Remark 1.1.4. Let
![]() $\mathfrak {Q}$
be a deformation of
$\mathfrak {Q}$
be a deformation of
![]() $\mathcal {Q}$
over R. The associated G-
$\mathcal {Q}$
over R. The associated G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}_{(\mathfrak {S}, (\mathcal {E}))}$
over
$\mathfrak {Q}_{(\mathfrak {S}, (\mathcal {E}))}$
over
![]() $(\mathfrak {S}, (\mathcal {E}))$
is a deformation of
$(\mathfrak {S}, (\mathcal {E}))$
is a deformation of
![]() $\mathcal {Q}$
(i.e., it is equipped with an isomorphism between
$\mathcal {Q}$
(i.e., it is equipped with an isomorphism between
![]() $\mathcal {Q}$
and the base change of
$\mathcal {Q}$
and the base change of
![]() $\mathfrak {Q}_{(\mathfrak {S}, (\mathcal {E}))}$
along the map
$\mathfrak {Q}_{(\mathfrak {S}, (\mathcal {E}))}$
along the map
![]() $(\mathfrak {S}, (\mathcal {E})) \to (W(k), (p))$
defined by
$(\mathfrak {S}, (\mathcal {E})) \to (W(k), (p))$
defined by
![]() $t_i \mapsto 0$
). The construction
$t_i \mapsto 0$
). The construction
![]() $\mathfrak {Q} \mapsto \mathfrak {Q}_{(\mathfrak {S}, (\mathcal {E}))}$
induces an equivalence from the category of deformations of
$\mathfrak {Q} \mapsto \mathfrak {Q}_{(\mathfrak {S}, (\mathcal {E}))}$
induces an equivalence from the category of deformations of
![]() $\mathcal {Q}$
over R to that of deformations of
$\mathcal {Q}$
over R to that of deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(\mathfrak {S}, (\mathcal {E}))$
. This is a consequence of [Reference ItoIto23, Theorem 1.2.1] (see also Theorem 2.6.5).
$(\mathfrak {S}, (\mathcal {E}))$
. This is a consequence of [Reference ItoIto23, Theorem 1.2.1] (see also Theorem 2.6.5).
Let
![]() $\mathfrak {Q}$
be a deformation of
$\mathfrak {Q}$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
. Let
$R_{G, \mu }$
. Let
![]() $ {\mathrm {Hom}} (R_{G, \mu }, R)_e$
be the set of local homomorphisms
$ {\mathrm {Hom}} (R_{G, \mu }, R)_e$
be the set of local homomorphisms
![]() $R_{G, \mu } \to R$
over
$R_{G, \mu } \to R$
over
![]() $W(k)$
. Given a homomorphism
$W(k)$
. Given a homomorphism
![]() $g \in {\mathrm {Hom}} (R_{G, \mu }, R)_e$
, we can regard
$g \in {\mathrm {Hom}} (R_{G, \mu }, R)_e$
, we can regard
![]() $(\mathfrak {S}, (\mathcal {E}))$
as an object of
$(\mathfrak {S}, (\mathcal {E}))$
as an object of ![]() . The construction
. The construction
![]() $g \mapsto \mathfrak {Q}_g$
induces a map of sets
$g \mapsto \mathfrak {Q}_g$
induces a map of sets
 $$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, R)_e \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (\mathfrak{S}, (\mathcal{E})) \end{array} \right\}, \end{align*}$$
$$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, R)_e \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (\mathfrak{S}, (\mathcal{E})) \end{array} \right\}, \end{align*}$$
which we call the evaluation map. If
![]() $\mathfrak {Q}$
is a universal deformation, then the map
$\mathfrak {Q}$
is a universal deformation, then the map
![]() $ {\mathrm {ev}} _{\mathfrak {Q}}$
is bijective by Remark 1.1.4. (In fact,
$ {\mathrm {ev}} _{\mathfrak {Q}}$
is bijective by Remark 1.1.4. (In fact,
![]() $\mathfrak {Q}$
is a universal deformation if and only if for every prism
$\mathfrak {Q}$
is a universal deformation if and only if for every prism
![]() $ (\mathfrak {S}, (\mathcal {E})) $
of Breuil–Kisin type, the map
$ (\mathfrak {S}, (\mathcal {E})) $
of Breuil–Kisin type, the map
![]() $ {\mathrm {ev}} _{\mathfrak {Q}}$
is bijective.)
$ {\mathrm {ev}} _{\mathfrak {Q}}$
is bijective.)
We also consider the following classes of deformations:
Definition 1.1.5. For every integer
![]() $m \geq 1$
, we set
$m \geq 1$
, we set
which is naturally a bounded prism. Let
![]() $ {\mathrm {Hom}} (R_{G, \mu }, R/\mathfrak {m}^{m}_R)_e$
be the set of local homomorphisms
$ {\mathrm {Hom}} (R_{G, \mu }, R/\mathfrak {m}^{m}_R)_e$
be the set of local homomorphisms
![]() $R_{G, \mu } \to R/\mathfrak {m}^{m}_R$
over
$R_{G, \mu } \to R/\mathfrak {m}^{m}_R$
over
![]() $W(k)$
, where
$W(k)$
, where
![]() $\mathfrak {m}_R \subset R$
is the maximal ideal. We have the following map defined by
$\mathfrak {m}_R \subset R$
is the maximal ideal. We have the following map defined by
![]() $g \mapsto \mathfrak {Q}_g$
:
$g \mapsto \mathfrak {Q}_g$
:
 $$ \begin{align} {\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, R/\mathfrak{m}^{m}_R)_e \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (\mathfrak{S}_m, (\mathcal{E})) \end{array} \right\}. \end{align} $$
$$ \begin{align} {\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, R/\mathfrak{m}^{m}_R)_e \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (\mathfrak{S}_m, (\mathcal{E})) \end{array} \right\}. \end{align} $$
Definition 1.1.6. Let S be a perfectoid ring over
![]() $W(k)$
([Reference Bhatt, Morrow and ScholzeBMS18, Definition 3.5]). Let
$W(k)$
([Reference Bhatt, Morrow and ScholzeBMS18, Definition 3.5]). Let
![]() $a^\flat \in S^\flat $
be an element such that
$a^\flat \in S^\flat $
be an element such that
![]() $a:=\theta ([a^\flat ]) \in S$
is a nonzerodivisor and
$a:=\theta ([a^\flat ]) \in S$
is a nonzerodivisor and
![]() $p=0$
in
$p=0$
in
![]() $S/a$
. (See Section 2.1 for the notation used here.) For every integer
$S/a$
. (See Section 2.1 for the notation used here.) For every integer
![]() $m \geq 1$
, the pair
$m \geq 1$
, the pair
is naturally a bounded prism, where
![]() $I_S$
is the kernel of the natural homomorphism
$I_S$
is the kernel of the natural homomorphism
![]() $\theta \colon W(S^\flat )/[a^\flat ]^m \to S/a^m$
. Let
$\theta \colon W(S^\flat )/[a^\flat ]^m \to S/a^m$
. Let
![]() $ {\mathrm {Hom}} (R_{G, \mu }, S/a^m)_{e}$
be the set of homomorphisms
$ {\mathrm {Hom}} (R_{G, \mu }, S/a^m)_{e}$
be the set of homomorphisms
![]() $R_{G, \mu } \to S/a^m$
over
$R_{G, \mu } \to S/a^m$
over
![]() $W(k)$
lifting the composition
$W(k)$
lifting the composition
![]() $R_{G, \mu } \to k \to S/a$
. We regard
$R_{G, \mu } \to k \to S/a$
. We regard
![]() $\mathcal {Q}$
as a G-
$\mathcal {Q}$
as a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(W(S^\flat )/[a^\flat ], I_S)$
by base change. We have the following map defined by
$(W(S^\flat )/[a^\flat ], I_S)$
by base change. We have the following map defined by
![]() $g \mapsto \mathfrak {Q}_g$
:
$g \mapsto \mathfrak {Q}_g$
:
 $$ \begin{align} {\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, S/a^m)_{e} \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of } \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (W(S^\flat)/[a^\flat]^m, I_S) \end{array} \right\}. \end{align} $$
$$ \begin{align} {\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, S/a^m)_{e} \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of } \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (W(S^\flat)/[a^\flat]^m, I_S) \end{array} \right\}. \end{align} $$
We can now state our second main result:
Theorem 1.1.7 (Theorem 4.1.7).
If
![]() $\mathfrak {Q}$
is a universal deformation of
$\mathfrak {Q}$
is a universal deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
, then the maps (1.1) and (1.2) are bijective.
$R_{G, \mu }$
, then the maps (1.1) and (1.2) are bijective.
Using the prism
![]() $(W(k)[[t]]/t^2, (p))$
, we have the following characterization of universal deformations of
$(W(k)[[t]]/t^2, (p))$
, we have the following characterization of universal deformations of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Theorem 1.1.8 (Theorem 4.1.8).
Let
![]() $\mathfrak {Q}$
be a deformation of
$\mathfrak {Q}$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
. If the map
$R_{G, \mu }$
. If the map
 $$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, k[[t]]/t^2)_{e} \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (W(k)[[t]]/t^2, (p)) \end{array} \right\} \end{align*}$$
$$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, k[[t]]/t^2)_{e} \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathcal{Q} \text{ over } (W(k)[[t]]/t^2, (p)) \end{array} \right\} \end{align*}$$
is surjective, then
![]() $\mathfrak {Q}$
is a universal deformation of
$\mathfrak {Q}$
is a universal deformation of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
The map
![]() $ {\mathrm {ev}} _{\mathfrak {Q}}$
as in Theorem 1.1.8 is called the Kodaira–Spencer map in this paper.
$ {\mathrm {ev}} _{\mathfrak {Q}}$
as in Theorem 1.1.8 is called the Kodaira–Spencer map in this paper.
Remark 1.1.9. In fact, by using
![]() ${\mathcal O}_E$
-prisms as introduced in [Reference MarksMar23] and [Reference ItoIto23], we will formulate and prove our results for a smooth affine group scheme G over the ring of integers
${\mathcal O}_E$
-prisms as introduced in [Reference MarksMar23] and [Reference ItoIto23], we will formulate and prove our results for a smooth affine group scheme G over the ring of integers
![]() ${\mathcal O}_E$
of any finite extension E of
${\mathcal O}_E$
of any finite extension E of
![]() ${\mathbb Q}_p$
. (In [Reference MarksMar23],
${\mathbb Q}_p$
. (In [Reference MarksMar23],
![]() ${\mathcal O}_E$
-prisms are called E-typical prisms.) The argument for general
${\mathcal O}_E$
-prisms are called E-typical prisms.) The argument for general
![]() ${\mathcal O}_E$
is the same as that for the case where
${\mathcal O}_E$
is the same as that for the case where
![]() ${\mathcal O}_E={\mathbb Z}_p$
. For simplicity, the reader may assume that
${\mathcal O}_E={\mathbb Z}_p$
. For simplicity, the reader may assume that
![]() ${\mathcal O}_E={\mathbb Z}_p$
on a first reading.
${\mathcal O}_E={\mathbb Z}_p$
on a first reading.
Let R be a quasisyntomic ring over
![]() $W(k)$
in the sense of [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.10]. In [Reference ItoIto23, Section 8.2], we defined the groupoid
$W(k)$
in the sense of [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.10]. In [Reference ItoIto23, Section 8.2], we defined the groupoid ![]() of prismatic G-F-gauges of type
of prismatic G-F-gauges of type
![]() $\mu $
over R and constructed a fully faithful functor
$\mu $
over R and constructed a fully faithful functor
following the theory of prismatic F-gauges introduced by Drinfeld and Bhatt–Lurie (cf. [Reference DrinfeldDri22], [Reference Bhatt and LurieBL22a], [Reference Bhatt and LurieBL22b], [Reference BhattBha22]). If R belongs to
![]() $\mathcal {C}_{W(k)}$
, then the above functor is an equivalence (Proposition 7.1.1). Thus, Theorem 1.1.3 can be rephrased as follows:
$\mathcal {C}_{W(k)}$
, then the above functor is an equivalence (Proposition 7.1.1). Thus, Theorem 1.1.3 can be rephrased as follows:
Theorem 1.1.10 (Theorem 7.2.1).
Let ![]() be a prismatic G-F-gauge of type
be a prismatic G-F-gauge of type
![]() $\mu $
over k. There exists a deformation
$\mu $
over k. There exists a deformation ![]() of
of
![]() $\mathscr {Q}$
over
$\mathscr {Q}$
over
![]() $R_{G, \mu }$
which is universal among deformations of
$R_{G, \mu }$
which is universal among deformations of
![]() $\mathscr {Q}$
over R with
$\mathscr {Q}$
over R with
![]() $R \in \mathcal {C}_{W(k)}$
.
$R \in \mathcal {C}_{W(k)}$
.
Remark 1.1.11. In light of Theorem 1.1.7, one can expect that
![]() $\mathscr {Q}^{\mathrm {univ}}$
is also universal among deformations of
$\mathscr {Q}^{\mathrm {univ}}$
is also universal among deformations of
![]() $\mathscr {Q}$
over
$\mathscr {Q}$
over
![]() $R/\mathfrak {m}^{m}_R$
with
$R/\mathfrak {m}^{m}_R$
with
![]() $R \in \mathcal {C}_{W(k)}$
such that
$R \in \mathcal {C}_{W(k)}$
such that
![]() $\dim R =1$
and over
$\dim R =1$
and over
![]() $S/a^m$
as in Definition 1.1.6. We note that
$S/a^m$
as in Definition 1.1.6. We note that
![]() $R/\mathfrak {m}^{m}_R$
(with
$R/\mathfrak {m}^{m}_R$
(with
![]() $\dim R =1$
) and
$\dim R =1$
) and
![]() $S/a^m$
are quasisyntomic. In principle, it should be possible to develop the deformation theory for prismatic G-F-gauges of type
$S/a^m$
are quasisyntomic. In principle, it should be possible to develop the deformation theory for prismatic G-F-gauges of type
![]() $\mu $
in a more conceptual (but rather abstract) way, and the results presented in this paper should provide a practical way to understand it by using G-
$\mu $
in a more conceptual (but rather abstract) way, and the results presented in this paper should provide a practical way to understand it by using G-
![]() $\mu $
-displays over prisms. We will only make some conjectures in Section 7 and will not pursue this direction here. See also Remark 1.1.13.
$\mu $
-displays over prisms. We will only make some conjectures in Section 7 and will not pursue this direction here. See also Remark 1.1.13.
Remark 1.1.12. Assume that G is reductive. In [Reference Bültel and PappasBP20], Bültel–Pappas introduced the notion of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $ \mathrm {Spec} R$
for any
$ \mathrm {Spec} R$
for any
![]() $W(k)$
-algebra R by using the ring
$W(k)$
-algebra R by using the ring
![]() $W(R)$
of p-typical Witt vectors. (In [Reference Bültel and PappasBP20], G-
$W(R)$
of p-typical Witt vectors. (In [Reference Bültel and PappasBP20], G-
![]() $\mu $
-displays are called
$\mu $
-displays are called
![]() $(G, \mu )$
-displays.) The groupoid of G-
$(G, \mu )$
-displays.) The groupoid of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $ \mathrm {Spec} k$
in their sense is equivalent to
$ \mathrm {Spec} k$
in their sense is equivalent to ![]() . Let
. Let
![]() $\mathcal {Q}$
be a (banal) G-
$\mathcal {Q}$
be a (banal) G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $ \mathrm {Spec} k$
. Under the assumption that
$ \mathrm {Spec} k$
. Under the assumption that
![]() $\mathcal {Q}$
is adjoint nilpotent in the sense of [Reference Bültel and PappasBP20, Definition 3.4.2], they proved that the deformation functor of
$\mathcal {Q}$
is adjoint nilpotent in the sense of [Reference Bültel and PappasBP20, Definition 3.4.2], they proved that the deformation functor of
![]() $\mathcal {Q}$
defined on the category
$\mathcal {Q}$
defined on the category
![]() $ {\mathrm {Art}} _{W(k)}$
of artinian local rings over
$ {\mathrm {Art}} _{W(k)}$
of artinian local rings over
![]() $W(k)$
with residue field k is pro-representable by
$W(k)$
with residue field k is pro-representable by
![]() $R_{G, \mu }$
. See [Reference Bültel and PappasBP20, 3.5.9] for details. The deformation theory developed in this paper applies to complete regular local rings
$R_{G, \mu }$
. See [Reference Bültel and PappasBP20, 3.5.9] for details. The deformation theory developed in this paper applies to complete regular local rings
![]() $R \in \mathcal {C}_{W(k)}$
and their quotients
$R \in \mathcal {C}_{W(k)}$
and their quotients
![]() $R/\mathfrak {m}^m_R$
without imposing any additional conditions on G-
$R/\mathfrak {m}^m_R$
without imposing any additional conditions on G-
![]() $\mu $
-displays, such as the adjoint nilpotent condition.
$\mu $
-displays, such as the adjoint nilpotent condition.
Remark 1.1.13. After this work was completed, and during the refereeing process, Gardner–Madapusi [Reference Gardner and MadapusiGM24] developed the deformation theory for prismatic G-F-gauges of type
![]() $\mu $
using the stacky approach of Drinfeld and Bhatt–Lurie, from which the conjectures stated in Section 7 will follow. More precisely, using their result, we can extend the definition of prismatic G-F-gauges of type
$\mu $
using the stacky approach of Drinfeld and Bhatt–Lurie, from which the conjectures stated in Section 7 will follow. More precisely, using their result, we can extend the definition of prismatic G-F-gauges of type
![]() $\mu $
to (not necessarily quasisyntomic) p-adically complete rings and then generalize our results to arbitrary artinian local rings in
$\mu $
to (not necessarily quasisyntomic) p-adically complete rings and then generalize our results to arbitrary artinian local rings in
![]() $ {\mathrm {Art}} _{W(k)}$
. Compared to [Reference Gardner and MadapusiGM24], the method developed in this paper cannot be applied to arbitrary artinian local rings, but it does not require the use of some powerful results on derived algebraic geometry, such as Lurie’s generalization of Artin’s representability theorem. See also [Reference Imai, Kato and YoucisIKY23] for the relation between our results and those in [Reference Gardner and MadapusiGM24].
$ {\mathrm {Art}} _{W(k)}$
. Compared to [Reference Gardner and MadapusiGM24], the method developed in this paper cannot be applied to arbitrary artinian local rings, but it does not require the use of some powerful results on derived algebraic geometry, such as Lurie’s generalization of Artin’s representability theorem. See also [Reference Imai, Kato and YoucisIKY23] for the relation between our results and those in [Reference Gardner and MadapusiGM24].
1.2 Applications
We give two applications of our results. Assume that G is a connected reductive group scheme over
![]() ${\mathbb Z}_p$
(or over
${\mathbb Z}_p$
(or over
![]() ${\mathcal O}_E$
). The first application concerns the local representability and the formal smoothness of the integral local Shimura variety
${\mathcal O}_E$
). The first application concerns the local representability and the formal smoothness of the integral local Shimura variety
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
with hyperspecial level structure, which is introduced in [Reference Scholze and WeinsteinSW20] as a v-sheaf on the category of perfectoid spaces of characteristic p. More precisely, we prove in Theorem 5.3.5 that the formal completions
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
with hyperspecial level structure, which is introduced in [Reference Scholze and WeinsteinSW20] as a v-sheaf on the category of perfectoid spaces of characteristic p. More precisely, we prove in Theorem 5.3.5 that the formal completions
![]() $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
of
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
of
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
introduced in [Reference GleasonGle22b] are representable by the formal scheme
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
introduced in [Reference GleasonGle22b] are representable by the formal scheme
![]() $ \mathrm {Spf} R_{G, \mu }$
(or rather
$ \mathrm {Spf} R_{G, \mu }$
(or rather
![]() $ \mathrm {Spf} R_{G, \mu ^{-1}}$
, depending on the sign convention) by relating
$ \mathrm {Spf} R_{G, \mu ^{-1}}$
, depending on the sign convention) by relating
![]() $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
to universal deformations of prismatic G-
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
to universal deformations of prismatic G-
![]() $\mu $
-displays.
$\mu $
-displays.
Remark 1.2.1. The above result (Theorem 5.3.5) implies that a conjecture of Pappas–Rapoport [Reference Pappas and RapoportPR24, Conjecture 3.3.5] in the hyperspecial case, which was originally proposed by Gleason [Reference GleasonGle21, Conjecture 1], holds true. In [Reference Pappas and RapoportPR22], Pappas–Rapoport proved their conjecture (in the more general case where G is parahoric) under the assumption that
![]() $p \geq 3$
and
$p \geq 3$
and
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is of abelian type. If
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is of abelian type. If
![]() $p=2$
, the same result was obtained under the additional assumption that
$p=2$
, the same result was obtained under the additional assumption that
![]() $G_{{\mathbb Q}_p}$
is of type A or C. Our approach is completely different from that of [Reference Pappas and RapoportPR22], and we do not need to impose these assumptions. Our result also generalizes a result of Bartling [Reference BartlingBar22], in which the adjoint nilpotent condition of [Reference Bültel and PappasBP20] is imposed. See Section 5.3 for details.
$G_{{\mathbb Q}_p}$
is of type A or C. Our approach is completely different from that of [Reference Pappas and RapoportPR22], and we do not need to impose these assumptions. Our result also generalizes a result of Bartling [Reference BartlingBar22], in which the adjoint nilpotent condition of [Reference Bültel and PappasBP20] is imposed. See Section 5.3 for details.
Remark 1.2.2. In [Reference Imai, Kato and YoucisIKY23], our universal deformations of prismatic G-
![]() $\mu $
-displays are used to give a prismatic characterization of integral canonical models of (global) Shimura varieties of abelian type with hyperspecial level structure, which is inspired by [Reference Pappas and RapoportPR24, Theorem 4.2.4].
$\mu $
-displays are used to give a prismatic characterization of integral canonical models of (global) Shimura varieties of abelian type with hyperspecial level structure, which is inspired by [Reference Pappas and RapoportPR24, Theorem 4.2.4].
As a second application, we revisit and extend some classification results of p-divisible groups.
Remark 1.2.3. Let R be a quasisyntomic ring. In [Reference Anschütz and Le BrasALB23], Anschütz–Le Bras constructed a contravariant functor from the category of p-divisible groups over
![]() $ \mathrm {Spec} R$
to the category of admissible prismatic Dieudonné crystals over R ([Reference Anschütz and Le BrasALB23, Definition 4.5]), which is called the prismatic Dieudonné functor. They proved that the prismatic Dieudonné functor is an anti-equivalence; see [Reference Anschütz and Le BrasALB23, Theorem 4.74]. For any
$ \mathrm {Spec} R$
to the category of admissible prismatic Dieudonné crystals over R ([Reference Anschütz and Le BrasALB23, Definition 4.5]), which is called the prismatic Dieudonné functor. They proved that the prismatic Dieudonné functor is an anti-equivalence; see [Reference Anschütz and Le BrasALB23, Theorem 4.74]. For any
![]() $R \in \mathcal {C}_{W(k)}$
, our prismatic
$R \in \mathcal {C}_{W(k)}$
, our prismatic
![]() $ {\mathrm {GL}} _N$
-
$ {\mathrm {GL}} _N$
-
![]() $\mu $
-displays over R can be viewed as admissible prismatic Dieudonné crystals over R (with some additional conditions). Then Theorem 1.1.3 and Theorem 1.1.8 follow immediately from [Reference Anschütz and Le BrasALB23, Theorem 4.74], together with the deformation theory for p-divisible groups. However, Theorem 1.1.7 is a new result as far as we know. The proofs of Theorem 1.1.3, Theorem 1.1.7 and Theorem 1.1.8 presented in this paper do not rely on p-divisible groups.
$\mu $
-displays over R can be viewed as admissible prismatic Dieudonné crystals over R (with some additional conditions). Then Theorem 1.1.3 and Theorem 1.1.8 follow immediately from [Reference Anschütz and Le BrasALB23, Theorem 4.74], together with the deformation theory for p-divisible groups. However, Theorem 1.1.7 is a new result as far as we know. The proofs of Theorem 1.1.3, Theorem 1.1.7 and Theorem 1.1.8 presented in this paper do not rely on p-divisible groups.
By using our results, we can give an alternative proof of the classification result of Anschütz–Le Bras mentioned above for any
![]() $R \in \mathcal {C}_{W(k)}$
. In fact, Theorem 1.1.7 enables us to prove the following results:
$R \in \mathcal {C}_{W(k)}$
. In fact, Theorem 1.1.7 enables us to prove the following results:
-
(1) (Theorem 6.3.2). Let the notation be as in Definition 1.1.5. For every
 $m \geq 1$
, the prismatic Dieudonné functor induces an anti-equivalence
$m \geq 1$
, the prismatic Dieudonné functor induces an anti-equivalence  $$\begin{align*}\left. \left\{ \begin{array}{c} \displaystyle p\text{-divisible groups} \\ \text{over } \mathrm{Spec} R/\mathfrak{m}^m_R \end{array} \right\} \right. \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle \text{minuscule Breuil--Kisin modules} \\ \displaystyle \text{over } (\mathfrak{S}_m, (\mathcal{E})) \end{array} \right\}. \end{align*}$$
$$\begin{align*}\left. \left\{ \begin{array}{c} \displaystyle p\text{-divisible groups} \\ \text{over } \mathrm{Spec} R/\mathfrak{m}^m_R \end{array} \right\} \right. \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle \text{minuscule Breuil--Kisin modules} \\ \displaystyle \text{over } (\mathfrak{S}_m, (\mathcal{E})) \end{array} \right\}. \end{align*}$$
-
(2) (Theorem 6.3.7). Let
 ${\mathcal O}_C$
be a p-adically complete valuation ring of rank
${\mathcal O}_C$
be a p-adically complete valuation ring of rank
 $1$
with algebraically closed fraction field C. Let
$1$
with algebraically closed fraction field C. Let
 $\varpi \in {\mathcal O}_C$
be a pseudo-uniformizer. For every
$\varpi \in {\mathcal O}_C$
be a pseudo-uniformizer. For every
 $m \geq 1$
, the prismatic Dieudonné functor induces an anti-equivalence
$m \geq 1$
, the prismatic Dieudonné functor induces an anti-equivalence  $$\begin{align*}\left. \left\{ \begin{array}{c} \displaystyle p\text{-divisible groups} \\ \text{ over } \mathrm{Spec} {\mathcal O}_C/\varpi^m \end{array} \right\} \right. \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle \text{minuscule Breuil--Kisin modules} \\ \displaystyle \text{over } (W({\mathcal O}_{C^\flat})/[\varpi^\flat]^{m}, I_{{\mathcal O}_C}) \end{array} \right\}. \end{align*}$$
$$\begin{align*}\left. \left\{ \begin{array}{c} \displaystyle p\text{-divisible groups} \\ \text{ over } \mathrm{Spec} {\mathcal O}_C/\varpi^m \end{array} \right\} \right. \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle \text{minuscule Breuil--Kisin modules} \\ \displaystyle \text{over } (W({\mathcal O}_{C^\flat})/[\varpi^\flat]^{m}, I_{{\mathcal O}_C}) \end{array} \right\}. \end{align*}$$
See Example 2.4.7 for the definition of minuscule Breuil–Kisin modules.
Remark 1.2.4. An equivalence as in (1) was previously obtained by Lau [Reference LauLau14] using Dieudonné displays and crystalline Dieudonné theory, where special efforts were made in the case of
![]() $p=2$
. (This result plays an essential role in the construction of
$p=2$
. (This result plays an essential role in the construction of
![]() $2$
-adic integral canonical models of Shimura varieties of abelian type with hyperspecial level structure in [Reference Kim and Madapusi PeraKMP16].)
$2$
-adic integral canonical models of Shimura varieties of abelian type with hyperspecial level structure in [Reference Kim and Madapusi PeraKMP16].)
By combining (2) with a theorem of Fargues [Reference Scholze and WeinsteinSW20, Theorem 14.1.1], we obtain an alternative proof of a result of Scholze–Weinstein [Reference Scholze and WeinsteinSW13, Theorem B], which says that, in the case where C is of characteristic
![]() $0$
, there exists an equivalence between the category of p-divisible groups over
$0$
, there exists an equivalence between the category of p-divisible groups over
![]() $ \mathrm { Spec} {\mathcal O}_C$
and the category of free
$ \mathrm { Spec} {\mathcal O}_C$
and the category of free
![]() ${\mathbb Z}_p$
-modules T of finite rank together with a C-subspace of
${\mathbb Z}_p$
-modules T of finite rank together with a C-subspace of
![]() $T \otimes _{{\mathbb Z}_p} C$
. See Section 6.3 for details.
$T \otimes _{{\mathbb Z}_p} C$
. See Section 6.3 for details.
1.3 Strategy of the proof
We remark that if there exists a deformation
![]() $\mathfrak {Q}$
of
$\mathfrak {Q}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
such that the maps (1.1) and (1.2) for
$R_{G, \mu }$
such that the maps (1.1) and (1.2) for
![]() $\mathfrak {Q}$
are bijective, then
$\mathfrak {Q}$
are bijective, then
![]() $\mathfrak {Q}$
is a universal deformation, and moreover, Theorem 1.1.8 follows immediately. We briefly explain how to construct such a deformation
$\mathfrak {Q}$
is a universal deformation, and moreover, Theorem 1.1.8 follows immediately. We briefly explain how to construct such a deformation
![]() $\mathfrak {Q}$
. We choose a certain prism
$\mathfrak {Q}$
. We choose a certain prism
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }, (\mathcal {E}^{ {\mathrm {univ}} }))$
of Breuil–Kisin type with an isomorphism
$(\mathfrak {S}^{ {\mathrm {univ}} }, (\mathcal {E}^{ {\mathrm {univ}} }))$
of Breuil–Kisin type with an isomorphism
![]() $R_{G, \mu } \simeq \mathfrak {S}^{ {\mathrm {univ}} }/\mathcal {E}^{ {\mathrm {univ}} }$
over
$R_{G, \mu } \simeq \mathfrak {S}^{ {\mathrm {univ}} }/\mathcal {E}^{ {\mathrm {univ}} }$
over
![]() $W(k)$
. By Remark 1.1.4, giving a deformation of
$W(k)$
. By Remark 1.1.4, giving a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
is equivalent to giving a deformation of
$R_{G, \mu }$
is equivalent to giving a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }, (\mathcal {E}^{ {\mathrm {univ}} }))$
. In practice, the latter is much easier. We will construct a deformation
$(\mathfrak {S}^{ {\mathrm {univ}} }, (\mathcal {E}^{ {\mathrm {univ}} }))$
. In practice, the latter is much easier. We will construct a deformation
![]() $\mathscr {Q}$
of
$\mathscr {Q}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }, (\mathcal {E}^{ {\mathrm {univ}} }))$
such that the maps (1.1) and (1.2) for the corresponding deformation
$(\mathfrak {S}^{ {\mathrm {univ}} }, (\mathcal {E}^{ {\mathrm {univ}} }))$
such that the maps (1.1) and (1.2) for the corresponding deformation
![]() $\mathfrak {Q}$
over
$\mathfrak {Q}$
over
![]() $R_{G, \mu }$
are bijective.
$R_{G, \mu }$
are bijective.
The key ingredient is the Grothendieck–Messing deformation theory for G-
![]() $\mu $
-displays developed in Section 3. Let
$\mu $
-displays developed in Section 3. Let
![]() $\mathcal {Q}'$
be a G-
$\mathcal {Q}'$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(\mathfrak {S}_m, (\mathcal {E}))$
(resp.
$(\mathfrak {S}_m, (\mathcal {E}))$
(resp.
![]() $(W(S^\flat )/[a^\flat ]^m, I_S)$
). Then the Grothendieck–Messing deformation theory says that deformations of
$(W(S^\flat )/[a^\flat ]^m, I_S)$
). Then the Grothendieck–Messing deformation theory says that deformations of
![]() $\mathcal {Q}'$
over
$\mathcal {Q}'$
over
![]() $(\mathfrak {S}_{m+1}, (\mathcal {E}))$
(resp.
$(\mathfrak {S}_{m+1}, (\mathcal {E}))$
(resp.
![]() $(W(S^\flat )/[a^\flat ]^{m+1}, I_S)$
) are classified by lifts of the Hodge filtration of
$(W(S^\flat )/[a^\flat ]^{m+1}, I_S)$
) are classified by lifts of the Hodge filtration of
![]() $\mathcal {Q}'$
; see Theorem 3.3.4 for the precise statement. Here, the 1-boundedness of
$\mathcal {Q}'$
; see Theorem 3.3.4 for the precise statement. Here, the 1-boundedness of
![]() $\mu $
is essential. In view of this result, it is not difficult to find a candidate for
$\mu $
is essential. In view of this result, it is not difficult to find a candidate for
![]() $\mathscr {Q}$
. In fact, our construction is an analogue of the construction of universal p-divisible groups given by Faltings [Reference FaltingsFal99, Section 7].
$\mathscr {Q}$
. In fact, our construction is an analogue of the construction of universal p-divisible groups given by Faltings [Reference FaltingsFal99, Section 7].
The proof of the bijectivity of the maps (1.1) and (1.2) for
![]() $\mathfrak {Q}$
goes as follows. We fix a homomorphism
$\mathfrak {Q}$
goes as follows. We fix a homomorphism
![]() $g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
and let
$g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
and let
![]() $ {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
be the set of homomorphisms
$ {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
be the set of homomorphisms
![]() $h \colon R_{G, \mu } \to S/a^{m+1}$
over
$h \colon R_{G, \mu } \to S/a^{m+1}$
over
![]() $W(k)$
which are lifts of g. To prove that the map (1.2) is bijective, it suffices to show that (for all m and g) the map
$W(k)$
which are lifts of g. To prove that the map (1.2) is bijective, it suffices to show that (for all m and g) the map
 $$ \begin{align} {\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, S/a^{m+1})_{g} \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathfrak{Q}_g \text{ over } (W(S^\flat)/[a^\flat]^{m+1}, I_S) \end{array} \right\} \end{align} $$
$$ \begin{align} {\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R_{G, \mu}, S/a^{m+1})_{g} \to \left\{ \begin{array}{c} \displaystyle \text{isomorphism classes of} \\ \displaystyle \text{deformations of } \mathfrak{Q}_g \text{ over } (W(S^\flat)/[a^\flat]^{m+1}, I_S) \end{array} \right\} \end{align} $$
defined by
![]() $h \mapsto \mathfrak {Q}_h$
is bijective. After choosing a lift
$h \mapsto \mathfrak {Q}_h$
is bijective. After choosing a lift
![]() $h \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
, we can endow the set
$h \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
, we can endow the set
![]() $ {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
with the structure of an
$ {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
with the structure of an
![]() $S/a$
-module such that h is the zero element. The target of the map (1.3) can be also regarded as an
$S/a$
-module such that h is the zero element. The target of the map (1.3) can be also regarded as an
![]() $S/a$
-module by the Grothendieck–Messing deformation theory. In fact, we will show that the map (1.3) is not only a bijection, but also an
$S/a$
-module by the Grothendieck–Messing deformation theory. In fact, we will show that the map (1.3) is not only a bijection, but also an
![]() $S/a$
-linear isomorphism (cf. Theorem 4.4.2). For this, we may assume that any element of S admits a p-power root by André’s flatness lemma, and then we can prove the assertion by explicit computation. From this more precise statement, we can deduce that the map (1.1) is bijective (cf. Proposition 4.3.10).
$S/a$
-linear isomorphism (cf. Theorem 4.4.2). For this, we may assume that any element of S admits a p-power root by André’s flatness lemma, and then we can prove the assertion by explicit computation. From this more precise statement, we can deduce that the map (1.1) is bijective (cf. Proposition 4.3.10).
1.4 The structure of this paper
This paper is organized as follows. In Section 2, we review the theory of
![]() ${\mathcal O}_E$
-prisms and G-
${\mathcal O}_E$
-prisms and G-
![]() $\mu $
-displays over (bounded)
$\mu $
-displays over (bounded)
![]() ${\mathcal O}_E$
-prisms. In Section 3, we prove some basic results on deformations of G-
${\mathcal O}_E$
-prisms. In Section 3, we prove some basic results on deformations of G-
![]() $\mu $
-displays and establish the Grothendieck–Messing deformation theory for G-
$\mu $
-displays and establish the Grothendieck–Messing deformation theory for G-
![]() $\mu $
-displays. In Section 4, we state and prove the main results of this paper.
$\mu $
-displays. In Section 4, we state and prove the main results of this paper.
In Section 5 and Section 6, we give applications of our results to integral local Shimura varieties and p-divisible groups, respectively. Finally, in Section 7, we discuss some consequences of our deformation theory on prismatic F-gauges, or more precisely, on prismatic G-F-gauges of type
![]() $\mu $
.
$\mu $
.
Notation
This paper is a continuation of our previous work [Reference ItoIto23]. Unless explicitly stated otherwise, we use definitions and notation from [Reference ItoIto23].
We recall some notation from [Reference ItoIto23]. All rings are commutative and unital. For a scheme X over
![]() $ \mathrm {Spec} R$
and a ring homomorphism
$ \mathrm {Spec} R$
and a ring homomorphism
![]() $f \colon R \to R'$
, the base change
$f \colon R \to R'$
, the base change
![]() $X \times _{ \mathrm {Spec} R} \mathrm {Spec} R'$
is denoted by
$X \times _{ \mathrm {Spec} R} \mathrm {Spec} R'$
is denoted by
![]() $X_{R'}$
or
$X_{R'}$
or
![]() $f^*X$
. We use similar notation for the base change of group schemes, p-divisible groups, etc. All actions of groups will be right actions, unless otherwise stated. A groupoid is a category whose morphisms are all invertible. For a category
$f^*X$
. We use similar notation for the base change of group schemes, p-divisible groups, etc. All actions of groups will be right actions, unless otherwise stated. A groupoid is a category whose morphisms are all invertible. For a category
![]() $\mathcal {C}$
, let
$\mathcal {C}$
, let
![]() $\mathcal {C}^{\simeq }$
be the largest groupoid contained in
$\mathcal {C}^{\simeq }$
be the largest groupoid contained in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
2 Review of prismatic G-
 $\mu $
-displays
$\mu $
-displays
Throughout this paper, we fix a prime number p. Let E be a finite extension of
![]() ${\mathbb Q}_p$
with ring of integers
${\mathbb Q}_p$
with ring of integers
![]() ${\mathcal O}_E$
and residue field
${\mathcal O}_E$
and residue field
![]() ${\mathbb F}_q$
. Here,
${\mathbb F}_q$
. Here,
![]() ${\mathbb F}_q$
is a finite field with q elements. We fix a uniformizer
${\mathbb F}_q$
is a finite field with q elements. We fix a uniformizer
![]() $\pi \in {\mathcal O}_E$
for simplicity. Let k be a perfect field containing
$\pi \in {\mathcal O}_E$
for simplicity. Let k be a perfect field containing
![]() ${\mathbb F}_q$
, and we set
${\mathbb F}_q$
, and we set
![]() $ {\mathcal O} := W(k) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E. $
Let G be a smooth affine group scheme over
$ {\mathcal O} := W(k) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E. $
Let G be a smooth affine group scheme over
![]() ${\mathcal O}_E$
and let
${\mathcal O}_E$
and let
![]() $ \mu \colon {\mathbb G}_m \to G_{{\mathcal O}}:=G \times _{ \mathrm {Spec} {\mathcal O}_E} \mathrm {Spec} {\mathcal O} $
be a cocharacter.
$ \mu \colon {\mathbb G}_m \to G_{{\mathcal O}}:=G \times _{ \mathrm {Spec} {\mathcal O}_E} \mathrm {Spec} {\mathcal O} $
be a cocharacter.
In this section, we first recall the notion of
![]() ${\mathcal O}_E$
-prisms as introduced in [Reference MarksMar23] and [Reference ItoIto23]. We also provide some preliminary results on certain specific
${\mathcal O}_E$
-prisms as introduced in [Reference MarksMar23] and [Reference ItoIto23]. We also provide some preliminary results on certain specific
![]() ${\mathcal O}_E$
-prisms which will be used in this paper. Then we review the definition and basic properties of G-
${\mathcal O}_E$
-prisms which will be used in this paper. Then we review the definition and basic properties of G-
![]() $\mu $
-displays over bounded
$\mu $
-displays over bounded
![]() ${\mathcal O}_E$
-prisms developed in [Reference ItoIto23]. More details can be found in [Reference ItoIto23].
${\mathcal O}_E$
-prisms developed in [Reference ItoIto23]. More details can be found in [Reference ItoIto23].
2.1
 ${\mathcal O}_E$
-prisms
${\mathcal O}_E$
-prisms
Let A be an
![]() ${\mathcal O}_E$
-algebra. A
${\mathcal O}_E$
-algebra. A
![]() $\delta _E$
-structure on A is a map
$\delta _E$
-structure on A is a map
![]() $\delta _E \colon A \to A$
of sets with the following properties:
$\delta _E \colon A \to A$
of sets with the following properties:
-
•
 $\delta _E(xy)=x^q\delta _E(y)+y^q\delta _E(x)+\pi \delta _E(x)\delta _E(y)$
.
$\delta _E(xy)=x^q\delta _E(y)+y^q\delta _E(x)+\pi \delta _E(x)\delta _E(y)$
. -
•
 $\delta _E(x+y)=\delta _E(x)+\delta _E(y)+(x^q+y^q-(x+y)^q)/\pi $
.
$\delta _E(x+y)=\delta _E(x)+\delta _E(y)+(x^q+y^q-(x+y)^q)/\pi $
. -
• For an element
 $x \in {\mathcal O}_E$
, we have
$x \in {\mathcal O}_E$
, we have
 $\delta _E(x)=(x-x^q)/\pi $
.
$\delta _E(x)=(x-x^q)/\pi $
.
A
![]() $\delta _E$
-ring is an
$\delta _E$
-ring is an
![]() ${\mathcal O}_E$
-algebra A equipped with a
${\mathcal O}_E$
-algebra A equipped with a
![]() $\delta _E$
-structure. We define
$\delta _E$
-structure. We define
Then
![]() $\phi _A$
is a homomorphism of
$\phi _A$
is a homomorphism of
![]() ${\mathcal O}_E$
-algebras and is a lift of the q-th power Frobenius
${\mathcal O}_E$
-algebras and is a lift of the q-th power Frobenius
![]() $A/\pi \to A/\pi $
,
$A/\pi \to A/\pi $
,
![]() $x \mapsto x^q$
. The homomorphism
$x \mapsto x^q$
. The homomorphism
![]() $\phi _A$
is called the Frobenius of the
$\phi _A$
is called the Frobenius of the
![]() $\delta _E$
-ring A. When there is no ambiguity, we omit the subscript and simply write
$\delta _E$
-ring A. When there is no ambiguity, we omit the subscript and simply write
![]() $\phi =\phi _A$
.
$\phi =\phi _A$
.
An
![]() ${\mathcal O}_E$
-prism is a pair
${\mathcal O}_E$
-prism is a pair
![]() $(A, I)$
of a
$(A, I)$
of a
![]() $\delta _E$
-ring A and a Cartier divisor
$\delta _E$
-ring A and a Cartier divisor
![]() $I \subset A$
such that A is derived
$I \subset A$
such that A is derived
![]() $(\pi , I)$
-adically complete and
$(\pi , I)$
-adically complete and
![]() $\pi \in I + \phi (I)A$
. We say that
$\pi \in I + \phi (I)A$
. We say that
![]() $(A, I)$
is bounded if
$(A, I)$
is bounded if
![]() $A/I$
has bounded
$A/I$
has bounded
![]() $p^\infty $
-torsion (i.e.,
$p^\infty $
-torsion (i.e.,
![]() $(A/I)[p^n]=(A/I)[p^\infty ]$
for some integer
$(A/I)[p^n]=(A/I)[p^\infty ]$
for some integer
![]() $n \geq 1$
). In this case, A is
$n \geq 1$
). In this case, A is
![]() $(\pi , I)$
-adically complete ([Reference ItoIto23, Remark 2.3.2]). If
$(\pi , I)$
-adically complete ([Reference ItoIto23, Remark 2.3.2]). If
![]() ${\mathcal O}_E={\mathbb Z}_p$
, then bounded
${\mathcal O}_E={\mathbb Z}_p$
, then bounded
![]() ${\mathcal O}_E$
-prisms are the same as bounded prisms in the sense of [Reference Bhatt and ScholzeBS22]. We say that
${\mathcal O}_E$
-prisms are the same as bounded prisms in the sense of [Reference Bhatt and ScholzeBS22]. We say that
![]() $(A, I)$
is orientable if I is principal. An
$(A, I)$
is orientable if I is principal. An
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $(A, I)$
with a homomorphism
$(A, I)$
with a homomorphism
![]() ${\mathcal O} \to A$
of
${\mathcal O} \to A$
of
![]() $\delta _E$
-rings is called an
$\delta _E$
-rings is called an
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
. We refer to [Reference MarksMar23] and [Reference ItoIto23] for details.
${\mathcal O}$
. We refer to [Reference MarksMar23] and [Reference ItoIto23] for details.
We give some examples of
![]() ${\mathcal O}_E$
-prisms, which play a central role in this paper. We set
${\mathcal O}_E$
-prisms, which play a central role in this paper. We set
for
![]() $n \geq 0$
, which admits a unique
$n \geq 0$
, which admits a unique
![]() $\delta _E$
-structure such that the Frobenius
$\delta _E$
-structure such that the Frobenius
![]() $\phi \colon \mathfrak {S}_{\mathcal O} \to \mathfrak {S}_{\mathcal O}$
is given by
$\phi \colon \mathfrak {S}_{\mathcal O} \to \mathfrak {S}_{\mathcal O}$
is given by
![]() $\phi (t_i)=t^q_i$
(
$\phi (t_i)=t^q_i$
(
![]() $1 \leq i \leq n$
). For every integer
$1 \leq i \leq n$
). For every integer
![]() $m \geq 1$
, the quotient
$m \geq 1$
, the quotient
admits a unique
![]() $\delta _E$
-structure that is compatible with the one on
$\delta _E$
-structure that is compatible with the one on
![]() $\mathfrak {S}_{\mathcal O}$
.
$\mathfrak {S}_{\mathcal O}$
.
Example 2.1.1. Let
![]() $\mathcal {E} \in \mathfrak {S}_{\mathcal O}$
be a formal power series whose constant term is a uniformizer of
$\mathcal {E} \in \mathfrak {S}_{\mathcal O}$
be a formal power series whose constant term is a uniformizer of
![]() ${\mathcal O}$
. The pair
${\mathcal O}$
. The pair
![]() $ (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) $
is a bounded
$ (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) $
is a bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
([Reference ItoIto23, Proposition 2.3.8]), which we call an
${\mathcal O}$
([Reference ItoIto23, Proposition 2.3.8]), which we call an
![]() ${\mathcal O}_E$
-prism of Breuil–Kisin type in this paper. Here, n could be any nonnegative integer. For any
${\mathcal O}_E$
-prism of Breuil–Kisin type in this paper. Here, n could be any nonnegative integer. For any
![]() $m \geq 1$
, the pair
$m \geq 1$
, the pair
![]() $ (\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E})) $
is also a bounded
$ (\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E})) $
is also a bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
. Here, we denote the image of
${\mathcal O}$
. Here, we denote the image of
![]() $\mathcal {E}$
in
$\mathcal {E}$
in
![]() $\mathfrak {S}_{{\mathcal O}, m}$
by the same symbol.
$\mathfrak {S}_{{\mathcal O}, m}$
by the same symbol.
Our next example is related to (integral) perfectoid rings. We refer to [Reference Bhatt, Morrow and ScholzeBMS18, Section 3] and [Reference Česnavičius and ScholzeČS24, Section 2] for the definition and basic properties of perfectoid rings.
Let S be a perfectoid ring over
![]() ${\mathcal O}$
(i.e., S is a perfectoid ring with a ring homomorphism
${\mathcal O}$
(i.e., S is a perfectoid ring with a ring homomorphism
![]() ${\mathcal O} \to S$
). Let
${\mathcal O} \to S$
). Let
![]() $ S^\flat :=\varprojlim _{x \mapsto x^p} S/p $
be the tilt of S, which is a perfect k-algebra. Then
$ S^\flat :=\varprojlim _{x \mapsto x^p} S/p $
be the tilt of S, which is a perfect k-algebra. Then
is naturally an
![]() ${\mathcal O}$
-algebra. Let
${\mathcal O}$
-algebra. Let
![]() $\phi \colon W_{{\mathcal O}_E}(S^\flat ) \to W_{{\mathcal O}_E}(S^\flat )$
be the base change of the q-th power Frobenius of
$\phi \colon W_{{\mathcal O}_E}(S^\flat ) \to W_{{\mathcal O}_E}(S^\flat )$
be the base change of the q-th power Frobenius of
![]() $W(S^\flat )$
. Since
$W(S^\flat )$
. Since
![]() $W_{{\mathcal O}_E}(S^\flat )$
is
$W_{{\mathcal O}_E}(S^\flat )$
is
![]() $\pi $
-torsion free, we obtain the corresponding
$\pi $
-torsion free, we obtain the corresponding
![]() $\delta _E$
-structure on
$\delta _E$
-structure on
![]() $W_{{\mathcal O}_E}(S^\flat )$
. Moreover, for any element
$W_{{\mathcal O}_E}(S^\flat )$
. Moreover, for any element
![]() $x \in S^\flat $
, the quotient
$x \in S^\flat $
, the quotient
![]() $W_{{\mathcal O}_E}(S^\flat )/[x]$
admits a unique
$W_{{\mathcal O}_E}(S^\flat )/[x]$
admits a unique
![]() $\delta _E$
-structure that is compatible with the one on
$\delta _E$
-structure that is compatible with the one on
![]() $W_{{\mathcal O}_E}(S^\flat )$
. Here,
$W_{{\mathcal O}_E}(S^\flat )$
. Here,
![]() $[-]$
denotes the Teichmüller lift.
$[-]$
denotes the Teichmüller lift.
We note the following fact.
Lemma 2.1.2. For any element
![]() $x \in S^\flat $
, the quotient
$x \in S^\flat $
, the quotient
![]() $W_{{\mathcal O}_E}(S^\flat )/[x]$
is
$W_{{\mathcal O}_E}(S^\flat )/[x]$
is
![]() $\pi $
-torsion free (or equivalently, p-torsion free).
$\pi $
-torsion free (or equivalently, p-torsion free).
Proof. Since
![]() $W({\mathbb F}_q) \to {\mathcal O}_E$
is flat, it is enough to show that
$W({\mathbb F}_q) \to {\mathcal O}_E$
is flat, it is enough to show that
![]() $W(S^\flat )/[x]$
is p-torsion free. Let
$W(S^\flat )/[x]$
is p-torsion free. Let
![]() $y \in W(S^\flat )$
be an element such that
$y \in W(S^\flat )$
be an element such that
![]() $py=[x]z$
for some
$py=[x]z$
for some
![]() $z \in W(S^\flat )$
. We want to show that
$z \in W(S^\flat )$
. We want to show that
![]() $y \in ([x])$
. For the Witt vector expansions
$y \in ([x])$
. For the Witt vector expansions
![]() $y=(y_0, y_1, \dotsc )$
and
$y=(y_0, y_1, \dotsc )$
and
![]() $z=(z_0, z_1, \dotsc )$
, the equality
$z=(z_0, z_1, \dotsc )$
, the equality
![]() $py=[x]z$
implies that
$py=[x]z$
implies that
![]() $y^p_i=x^{p^{i+1}}z_{i+1}$
for every
$y^p_i=x^{p^{i+1}}z_{i+1}$
for every
![]() $i \geq 0$
. Since
$i \geq 0$
. Since
![]() $S^\flat $
is perfect, we have
$S^\flat $
is perfect, we have
![]() $y_i=x^{p^{i}}z^{1/p}_{i+1}$
for every
$y_i=x^{p^{i}}z^{1/p}_{i+1}$
for every
![]() $i \geq 0$
, and thus,
$i \geq 0$
, and thus,
![]() $ y=(y_0, y_1, \dotsc )=[x]\cdot (z^{1/p}_{1}, z^{1/p}_{2}, \dotsc ) \in ([x]). $
$ y=(y_0, y_1, \dotsc )=[x]\cdot (z^{1/p}_{1}, z^{1/p}_{2}, \dotsc ) \in ([x]). $
Let
![]() $ \theta \colon W(S^\flat ) \to S $
be the unique ring homomorphism whose reduction modulo p is the projection map
$ \theta \colon W(S^\flat ) \to S $
be the unique ring homomorphism whose reduction modulo p is the projection map
![]() $S^\flat \to S/p$
,
$S^\flat \to S/p$
,
![]() $(x_0, x_1, \dotsc ) \mapsto x_0$
. Let
$(x_0, x_1, \dotsc ) \mapsto x_0$
. Let
![]() $\theta _{{\mathcal O}_E} \colon W_{{\mathcal O}_E}(S^\flat ) \to S$
be the homomorphism induced from
$\theta _{{\mathcal O}_E} \colon W_{{\mathcal O}_E}(S^\flat ) \to S$
be the homomorphism induced from
![]() $\theta $
. We write
$\theta $
. We write
![]() $I_S:= {\mathrm {Ker}} \theta _{{\mathcal O}_E}$
for the kernel of
$I_S:= {\mathrm {Ker}} \theta _{{\mathcal O}_E}$
for the kernel of
![]() $\theta _{{\mathcal O}_E}$
.
$\theta _{{\mathcal O}_E}$
.
Proposition 2.1.3. Let S be a perfectoid ring over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
-
(1) The pair
 $ (W_{{\mathcal O}_E}(S^\flat ), I_S) $
is an orientable and bounded
$ (W_{{\mathcal O}_E}(S^\flat ), I_S) $
is an orientable and bounded
 ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
 ${\mathcal O}$
.
${\mathcal O}$
. -
(2) Let
 $a^\flat \in S^\flat $
be an element such that
$a^\flat \in S^\flat $
be an element such that
 $a:=\theta ([a^\flat ]) \in S$
is a nonzerodivisor and we have
$a:=\theta ([a^\flat ]) \in S$
is a nonzerodivisor and we have
 $\pi \in (a)$
in S. Let
$\pi \in (a)$
in S. Let
 $m \geq 1$
be an integer. Then is an orientable and bounded
$m \geq 1$
be an integer. Then is an orientable and bounded $$\begin{align*}(W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^m, I_S) \end{align*}$$
$$\begin{align*}(W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^m, I_S) \end{align*}$$
 ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
 ${\mathcal O}$
. Here, we denote the image of
${\mathcal O}$
. Here, we denote the image of
 $I_S$
in
$I_S$
in
 $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
by the same notation.
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
by the same notation.
Proof. (1) See [Reference ItoIto23, Proposition 2.4.3].
(2) We write
![]() $A_m:=W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
. Let
$A_m:=W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
. Let
![]() $\xi \in I_S$
be a generator. We shall show that
$\xi \in I_S$
be a generator. We shall show that
![]() $\xi $
is a nonzerodivisor in
$\xi $
is a nonzerodivisor in
![]() $A_m$
. Let
$A_m$
. Let
![]() $x, y \in W_{{\mathcal O}_E}(S^\flat )$
be elements satisfying
$x, y \in W_{{\mathcal O}_E}(S^\flat )$
be elements satisfying
![]() $\xi x=[a^\flat ]^m y$
. Since
$\xi x=[a^\flat ]^m y$
. Since
![]() $a \in S$
is a nonzerodivisor, we have
$a \in S$
is a nonzerodivisor, we have
![]() $y \in I_S=(\xi )$
. Since
$y \in I_S=(\xi )$
. Since
![]() $\xi $
is a nonzerodivisor in
$\xi $
is a nonzerodivisor in
![]() $W_{{\mathcal O}_E}(S^\flat )$
, we obtain
$W_{{\mathcal O}_E}(S^\flat )$
, we obtain
![]() $x \in ([a^\flat ]^m)$
. This proves that
$x \in ([a^\flat ]^m)$
. This proves that
![]() $\xi $
is a nonzerodivisor in
$\xi $
is a nonzerodivisor in
![]() $A_m$
. Moreover, since
$A_m$
. Moreover, since
![]() $\pi \in (\xi , \phi (\xi ))$
in
$\pi \in (\xi , \phi (\xi ))$
in
![]() $W_{{\mathcal O}_E}(S^\flat )$
by (1), we have
$W_{{\mathcal O}_E}(S^\flat )$
by (1), we have
![]() $\pi \in (\xi , \phi (\xi ))$
in
$\pi \in (\xi , \phi (\xi ))$
in
![]() $A_m$
as well.
$A_m$
as well.
The above argument, together with the fact that
![]() $W_{{\mathcal O}_E}(S^\flat )$
is
$W_{{\mathcal O}_E}(S^\flat )$
is
![]() $\xi $
-adically complete, implies that
$\xi $
-adically complete, implies that
![]() $W_{{\mathcal O}_E}(S^\flat )$
is
$W_{{\mathcal O}_E}(S^\flat )$
is
![]() $[a^\flat ]$
-torsion free. Since
$[a^\flat ]$
-torsion free. Since
![]() $W_{{\mathcal O}_E}(S^\flat )$
is derived
$W_{{\mathcal O}_E}(S^\flat )$
is derived
![]() $(\pi , \xi )$
-adically complete, so is
$(\pi , \xi )$
-adically complete, so is
![]() $A_m$
. It is clear that
$A_m$
. It is clear that
![]() $A_m/\xi =S/a^m$
has bounded
$A_m/\xi =S/a^m$
has bounded
![]() $p^\infty $
-torsion (since
$p^\infty $
-torsion (since
![]() $p^m$
=0 in
$p^m$
=0 in
![]() $S/a^m$
). In conclusion,
$S/a^m$
). In conclusion,
![]() $(A_m, I_S)$
is an orientable and bounded
$(A_m, I_S)$
is an orientable and bounded
![]() ${\mathcal O}_E$
-prism.
${\mathcal O}_E$
-prism.
For the purposes of this paper, it will be convenient to introduce the following (slightly nonstandard) definition:
Definition 2.1.4. A pair
![]() $(S, a^\flat )$
consisting of a perfectoid ring S over
$(S, a^\flat )$
consisting of a perfectoid ring S over
![]() ${\mathcal O}$
and an element
${\mathcal O}$
and an element
![]() $a^\flat \in S^\flat $
is called a perfectoid pair over
$a^\flat \in S^\flat $
is called a perfectoid pair over
![]() ${\mathcal O}$
if
${\mathcal O}$
if
![]() $a:=\theta ([a^\flat ]) \in S$
is a nonzerodivisor and we have
$a:=\theta ([a^\flat ]) \in S$
is a nonzerodivisor and we have
![]() $\pi \in (a)$
in S.
$\pi \in (a)$
in S.
2.2 Prismatic sites
We say that a map
![]() $(A, I) \to (A', I')$
of bounded
$(A, I) \to (A', I')$
of bounded
![]() ${\mathcal O}_E$
-prisms is a flat map (resp. a faithfully flat map) if
${\mathcal O}_E$
-prisms is a flat map (resp. a faithfully flat map) if
![]() $A \to A'$
is
$A \to A'$
is
![]() $(\pi ,I)$
-completely flat (resp.
$(\pi ,I)$
-completely flat (resp.
![]() $(\pi ,I)$
-completely faithfully flat) in the sense of [Reference Bhatt and ScholzeBS22, Notation 1.2].
$(\pi ,I)$
-completely faithfully flat) in the sense of [Reference Bhatt and ScholzeBS22, Notation 1.2].
Let R be a
![]() $\pi $
-adically complete
$\pi $
-adically complete
![]() ${\mathcal O}_E$
-algebra. As in [Reference ItoIto23, Definition 2.5.3], let
${\mathcal O}_E$
-algebra. As in [Reference ItoIto23, Definition 2.5.3], let
be the category of bounded
![]() ${\mathcal O}_E$
-prisms
${\mathcal O}_E$
-prisms
![]() $(A, I)$
together with a homomorphism
$(A, I)$
together with a homomorphism
![]() $R \to A/I$
of
$R \to A/I$
of
![]() ${\mathcal O}_E$
-algebras. We endow the opposite category
${\mathcal O}_E$
-algebras. We endow the opposite category ![]() with the flat topology – that is, the topology generated by the faithfully flat maps. It follows from [Reference ItoIto23, Remark 2.5.4] that
with the flat topology – that is, the topology generated by the faithfully flat maps. It follows from [Reference ItoIto23, Remark 2.5.4] that ![]() is a site. If
is a site. If
![]() ${\mathcal O}_E={\mathbb Z}_p$
, then
${\mathcal O}_E={\mathbb Z}_p$
, then ![]() is the same as the category
is the same as the category ![]() introduced in [Reference Bhatt and ScholzeBS22, Remark 4.7].
introduced in [Reference Bhatt and ScholzeBS22, Remark 4.7].
Remark 2.2.1. The functors

form sheaves with respect to the flat topology. Here,
![]() $\mathrm {Set}$
is the category of sets.
$\mathrm {Set}$
is the category of sets.
Let
![]() $(A, I)$
be a bounded
$(A, I)$
be a bounded
![]() ${\mathcal O}_E$
-prism. We write
${\mathcal O}_E$
-prism. We write
for the category of
![]() $(\pi , I)$
-completely étale A-algebras (in the sense of [Reference Bhatt and ScholzeBS22, Notation 1.2]). We endow
$(\pi , I)$
-completely étale A-algebras (in the sense of [Reference Bhatt and ScholzeBS22, Notation 1.2]). We endow
![]() $ (A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}} $
with the
$ (A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}} $
with the
![]() $(\pi , I)$
-completely étale topology – that is, the topology generated by the
$(\pi , I)$
-completely étale topology – that is, the topology generated by the
![]() $(\pi , I)$
-completely étale coverings
$(\pi , I)$
-completely étale coverings
![]() $B \to B'$
(i.e.,
$B \to B'$
(i.e.,
![]() $B \to B'$
is
$B \to B'$
is
![]() $(\pi , I)$
-completely étale and
$(\pi , I)$
-completely étale and
![]() $(\pi , I)$
-completely faithfully flat). Every
$(\pi , I)$
-completely faithfully flat). Every
![]() $B \in (A, I)_{\mathrm {\acute {e}t}}$
admits a unique
$B \in (A, I)_{\mathrm {\acute {e}t}}$
admits a unique
![]() $\delta _E$
-structure compatible with that on A, and the pair
$\delta _E$
-structure compatible with that on A, and the pair
![]() $(B, IB)$
is a bounded
$(B, IB)$
is a bounded
![]() ${\mathcal O}_E$
-prism by [Reference ItoIto23, Lemma 2.5.10].
${\mathcal O}_E$
-prism by [Reference ItoIto23, Lemma 2.5.10].
We recall the following fact (see [Reference ItoIto23, Example 2.5.11] and the references therein):
Example 2.2.2. Let S be a perfectoid ring over
![]() ${\mathcal O}_E$
and let
${\mathcal O}_E$
and let
![]() $S \to S'$
be a
$S \to S'$
be a
![]() $\pi $
-completely étale homomorphism. Then
$\pi $
-completely étale homomorphism. Then
![]() $S'$
is a perfectoid ring, and the induced homomorphism
$S'$
is a perfectoid ring, and the induced homomorphism
![]() $W_{{\mathcal O}_E}(S^\flat ) \to W_{{\mathcal O}_E}(S^{\prime \flat })$
is
$W_{{\mathcal O}_E}(S^\flat ) \to W_{{\mathcal O}_E}(S^{\prime \flat })$
is
![]() $(\pi , I_S)$
-completely étale.
$(\pi , I_S)$
-completely étale.
Lemma 2.2.3. Let
![]() $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
-
(1) For a
 $\pi $
-completely flat S-algebra
$\pi $
-completely flat S-algebra
 $S'$
, the element a is a nonzerodivisor in
$S'$
, the element a is a nonzerodivisor in
 $S'$
. In particular, if
$S'$
. In particular, if
 $S'$
is a perfectoid ring, then
$S'$
is a perfectoid ring, then
 $(S', a^\flat )$
is a perfectoid pair over
$(S', a^\flat )$
is a perfectoid pair over
 ${\mathcal O}$
.
${\mathcal O}$
. -
(2) For a
 $\pi $
-completely étale S-algebra
$\pi $
-completely étale S-algebra
 $S'$
, the homomorphism is
$S'$
, the homomorphism is $$\begin{align*}W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^m \to W_{{\mathcal O}_E}(S^{\prime\flat})/[a^\flat]^m \end{align*}$$
$$\begin{align*}W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^m \to W_{{\mathcal O}_E}(S^{\prime\flat})/[a^\flat]^m \end{align*}$$
 $(\pi , I_S)$
-completely étale for every
$(\pi , I_S)$
-completely étale for every
 $m \geq 1$
. Conversely, any
$m \geq 1$
. Conversely, any
 $(\pi , I_S)$
-completely étale
$(\pi , I_S)$
-completely étale
 $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
-algebra is of the form
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
-algebra is of the form
 $W_{{\mathcal O}_E}(S^{\prime \flat })/[a^\flat ]^m$
for some
$W_{{\mathcal O}_E}(S^{\prime \flat })/[a^\flat ]^m$
for some
 $\pi $
-completely étale S-algebra
$\pi $
-completely étale S-algebra
 $S'$
.
$S'$
.
Proof. (1) Since
![]() $\pi =0$
in
$\pi =0$
in
![]() $S/a$
, we see that
$S/a$
, we see that
![]() $S' \otimes ^{{\mathbb L}}_S S/a$
is concentrated in degree
$S' \otimes ^{{\mathbb L}}_S S/a$
is concentrated in degree
![]() $0$
. This means that a is a nonzerodivisor in
$0$
. This means that a is a nonzerodivisor in
![]() $S'$
.
$S'$
.
(2) This immediately follows from (1). See also the proof of [Reference ItoIto23, Lemma 2.5.9].
2.3 Display groups
Let A be an
![]() ${\mathcal O}$
-algebra and
${\mathcal O}$
-algebra and
![]() $I \subset A$
an ideal generated by a nonzerodivisor
$I \subset A$
an ideal generated by a nonzerodivisor
![]() $d \in A$
. We assume that A is I-adically complete. We set
$d \in A$
. We assume that A is I-adically complete. We set
![]() $A[1/I]:=A[1/d]$
. As in [Reference ItoIto23, Section 4], the display group
$A[1/I]:=A[1/d]$
. As in [Reference ItoIto23, Section 4], the display group
![]() $G_\mu (A, I)$
is defined by
$G_\mu (A, I)$
is defined by
We shall recall a structural result about
![]() $G_\mu (A, I)$
.
$G_\mu (A, I)$
.
Let
![]() $P_\mu , U^{-}_{\mu } \subset G_{\mathcal O}$
be the closed subgroup schemes defined by, for every
$P_\mu , U^{-}_{\mu } \subset G_{\mathcal O}$
be the closed subgroup schemes defined by, for every
![]() ${\mathcal O}$
-algebra R,
${\mathcal O}$
-algebra R,
 $$ \begin{align*} P_\mu(R)&=\{ \, g \in G(R) \, \vert \, \lim_{t \to 0} \mu(t)g\mu(t)^{-1} \, \text{exists} \, \},\\ U^{-}_{\mu}(R)&=\{ \, g \in G(R) \, \vert \, \lim_{t \to 0} \mu(t)^{-1}g\mu(t)=1 \, \}. \end{align*} $$
$$ \begin{align*} P_\mu(R)&=\{ \, g \in G(R) \, \vert \, \lim_{t \to 0} \mu(t)g\mu(t)^{-1} \, \text{exists} \, \},\\ U^{-}_{\mu}(R)&=\{ \, g \in G(R) \, \vert \, \lim_{t \to 0} \mu(t)^{-1}g\mu(t)=1 \, \}. \end{align*} $$
The group schemes
![]() $P_\mu $
and
$P_\mu $
and
![]() $U^{-}_{\mu }$
are smooth over
$U^{-}_{\mu }$
are smooth over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Definition 2.3.1 [Reference LauLau21, Definition 6.3.1].
The cocharacter
![]() $\mu \colon {\mathbb G}_m \to G_{{\mathcal O}}$
is called 1-bounded if the weights of the action of
$\mu \colon {\mathbb G}_m \to G_{{\mathcal O}}$
is called 1-bounded if the weights of the action of
![]() ${\mathbb G}_m$
on the Lie algebra
${\mathbb G}_m$
on the Lie algebra
![]() $ {\mathrm {Lie}} (G_{\mathcal O})$
induced by
$ {\mathrm {Lie}} (G_{\mathcal O})$
induced by
![]() $g \mapsto \mu (t)^{-1}g\mu (t)$
are
$g \mapsto \mu (t)^{-1}g\mu (t)$
are
![]() $\leq 1$
.
$\leq 1$
.
Remark 2.3.2. If G is a reductive group scheme over
![]() ${\mathcal O}_E$
, then
${\mathcal O}_E$
, then
![]() $\mu $
is 1-bounded if and only if
$\mu $
is 1-bounded if and only if
![]() $\mu $
is minuscule.
$\mu $
is minuscule.
Proposition 2.3.3.
-
(1) We have
 $P_\mu (A) \subset G_\mu (A, I)$
, and the image of
$P_\mu (A) \subset G_\mu (A, I)$
, and the image of
 $G_\mu (A, I)$
under the the projection
$G_\mu (A, I)$
under the the projection
 $G(A) \to G(A/I)$
is equal to
$G(A) \to G(A/I)$
is equal to
 $P_\mu (A/I)$
.
$P_\mu (A/I)$
. -
(2) The multiplication map
is bijiective. $$\begin{align*}(U^{-}_{\mu}(A) \cap G_\mu(A, I)) \times P_\mu(A) \to G_\mu(A, I) \end{align*}$$
$$\begin{align*}(U^{-}_{\mu}(A) \cap G_\mu(A, I)) \times P_\mu(A) \to G_\mu(A, I) \end{align*}$$
-
(3) Assume that
 $\mu $
is 1-bounded. Then
$\mu $
is 1-bounded. Then
 $G_\mu (A, I)$
coincides with the inverse image of
$G_\mu (A, I)$
coincides with the inverse image of
 $P_\mu (A/I)$
in
$P_\mu (A/I)$
in
 $G(A)$
under the projection
$G(A)$
under the projection
 $G(A) \to G(A/I)$
. Moreover, we have the following bijection:
$G(A) \to G(A/I)$
. Moreover, we have the following bijection:  $$\begin{align*}G(A)/G_\mu(A, I) \overset{\sim}{\to} G(A/I)/P_\mu(A/I). \end{align*}$$
$$\begin{align*}G(A)/G_\mu(A, I) \overset{\sim}{\to} G(A/I)/P_\mu(A/I). \end{align*}$$
Proof. The assertion (1) follows from [Reference ItoIto23, Lemma 4.2.2]. The assertion (2) is [Reference ItoIto23, Proposition 4.2.8]. For the assertion (3), see [Reference ItoIto23, Proposition 4.2.9].
2.4
G-
 $\mu $
-displays
$\mu $
-displays
Let
![]() $(A, I)$
be a bounded
$(A, I)$
be a bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
. We recall the definition of G-
${\mathcal O}$
. We recall the definition of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
.
$(A, I)$
.
We assume for a moment that
![]() $(A, I)$
is orientable. The results in Section 2.3 apply to
$(A, I)$
is orientable. The results in Section 2.3 apply to
![]() $(A, I)$
. In particular, we have the display group
$(A, I)$
. In particular, we have the display group
![]() $G_\mu (A, I)$
. For each generator
$G_\mu (A, I)$
. For each generator
![]() $d \in I$
, we define the following homomorphism:
$d \in I$
, we define the following homomorphism:
Let
![]() $G(A)_d$
be the set
$G(A)_d$
be the set
![]() $G(A)$
together with the following action of
$G(A)$
together with the following action of
![]() $G_\mu (A, I)$
:
$G_\mu (A, I)$
:
For another generator
![]() $d' \in I$
, we have
$d' \in I$
, we have
![]() $d=ud'$
for a unique
$d=ud'$
for a unique
![]() $u \in A^\times $
. The map
$u \in A^\times $
. The map
![]() $G(A)_d \to G(A)_{d'}$
defined by
$G(A)_d \to G(A)_{d'}$
defined by
![]() $X \mapsto X\phi (\mu (u))$
is
$X \mapsto X\phi (\mu (u))$
is
![]() $G_\mu (A, I)$
-equivariant. Thus, we can define
$G_\mu (A, I)$
-equivariant. Thus, we can define
where d runs over the set of generators
![]() $d \in I$
. The set
$d \in I$
. The set
![]() $G(A)_I$
carries a natural action of
$G(A)_I$
carries a natural action of
![]() $G_\mu (A, I)$
. The projection map
$G_\mu (A, I)$
. The projection map
![]() $G(A)_I \to G(A)_d$
is a
$G(A)_I \to G(A)_d$
is a
![]() $G_\mu (A, I)$
-equivariant bijection. For an element
$G_\mu (A, I)$
-equivariant bijection. For an element
![]() $X \in G(A)_I$
, let
$X \in G(A)_I$
, let
denote the image of X.
Let
![]() $G_{\mu , A, I}$
and
$G_{\mu , A, I}$
and ![]() be the sheaves on
be the sheaves on
![]() $(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
defined by
$(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
defined by
respectively. The sheaf ![]() is equipped with a natural action of the group sheaf
is equipped with a natural action of the group sheaf
![]() $G_{\mu , A, I}$
. In fact, we can extend these definitions to (not necessarily orientable) bounded
$G_{\mu , A, I}$
. In fact, we can extend these definitions to (not necessarily orientable) bounded
![]() ${\mathcal O}_E$
-prisms
${\mathcal O}_E$
-prisms
![]() $(A, I)$
over
$(A, I)$
over
![]() ${\mathcal O}$
; see [Reference ItoIto23, Section 4.3] for details.
${\mathcal O}$
; see [Reference ItoIto23, Section 4.3] for details.
Definition 2.4.1 (G-
 $\mu $
-display).
$\mu $
-display).
Let
![]() $(A, I)$
be a bounded
$(A, I)$
be a bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
. A G-
${\mathcal O}$
. A G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
is a pair
$(A, I)$
is a pair
where
![]() $\mathcal {Q}$
is a
$\mathcal {Q}$
is a
![]() $G_{\mu , A, I}$
-torsor and
$G_{\mu , A, I}$
-torsor and ![]() is a
is a
![]() $G_{\mu , A, I}$
-equivariant map of sheaves on
$G_{\mu , A, I}$
-equivariant map of sheaves on
![]() $(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
. When there is no possibility of confusion, we write
$(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
. When there is no possibility of confusion, we write
![]() $\mathcal {Q}$
instead of
$\mathcal {Q}$
instead of
![]() $(\mathcal {Q}, \alpha _{\mathcal {Q}})$
. We say that
$(\mathcal {Q}, \alpha _{\mathcal {Q}})$
. We say that
![]() $(\mathcal {Q}, \alpha _{\mathcal {Q}})$
is banal if
$(\mathcal {Q}, \alpha _{\mathcal {Q}})$
is banal if
![]() $\mathcal {Q}$
is a trivial
$\mathcal {Q}$
is a trivial
![]() $G_{\mu , A, I}$
-torsor.
$G_{\mu , A, I}$
-torsor.
Isomorphisms between G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
are defined in the obvious way. We write
$(A, I)$
are defined in the obvious way. We write
for the groupoid of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
and the groupoid of banal G-
$(A, I)$
and the groupoid of banal G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
, respectively.
$(A, I)$
, respectively.
Remark 2.4.2. Assume that
![]() $(A, I)$
is orientable. Let
$(A, I)$
is orientable. Let
![]() $ [G(A)_I/G_\mu (A, I)] $
be the groupoid whose objects are the elements
$ [G(A)_I/G_\mu (A, I)] $
be the groupoid whose objects are the elements
![]() $X \in G(A)_I$
and whose morphisms are defined by
$X \in G(A)_I$
and whose morphisms are defined by
Here,
![]() $(-)\cdot g$
denotes the action of
$(-)\cdot g$
denotes the action of
![]() $g \in G_\mu (A, I)$
. To each
$g \in G_\mu (A, I)$
. To each
![]() $X \in G(A)_I$
, we attach a banal G-
$X \in G(A)_I$
, we attach a banal G-
![]() $\mu $
-display
$\mu $
-display
over
![]() $(A, I)$
, where
$(A, I)$
, where ![]() is given by
is given by
![]() $1 \mapsto X$
. This construction gives an equivalence
$1 \mapsto X$
. This construction gives an equivalence ![]() of groupoids.
of groupoids.
For a map
![]() $f \colon (A, I) \to (A', I')$
of bounded
$f \colon (A, I) \to (A', I')$
of bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
, we have a base change functor
${\mathcal O}$
, we have a base change functor
More precisely, we have a fibered category
over ![]() .
.
Remark 2.4.3. Assume that
![]() $(A, I)$
is orientable. For an element
$(A, I)$
is orientable. For an element
![]() $X \in G(A)_I$
, let
$X \in G(A)_I$
, let
![]() $f(X) \in G(A')_{I'}$
be the unique element such that for any generator
$f(X) \in G(A')_{I'}$
be the unique element such that for any generator
![]() $d \in I$
, we have
$d \in I$
, we have
![]() $f(X)_{f(d)}=f(X_d)$
in
$f(X)_{f(d)}=f(X_d)$
in
![]() $G(A')$
. Then we have
$G(A')$
. Then we have
![]() $f^*(\mathcal {Q}_X)=\mathcal {Q}_{f(X)}$
for every
$f^*(\mathcal {Q}_X)=\mathcal {Q}_{f(X)}$
for every
![]() $X \in G(A)_I$
.
$X \in G(A)_I$
.
In the following, we recall more concrete descriptions of G-
![]() $\mu $
-displays. Let
$\mu $
-displays. Let
![]() $(A, I)$
be a bounded
$(A, I)$
be a bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Definition 2.4.4. A G-Breuil–Kisin module over
![]() $(A, I)$
is a G-torsor
$(A, I)$
is a G-torsor
![]() $\mathcal {P}$
over
$\mathcal {P}$
over
![]() $ \mathrm {Spec} A$
(with respect to the étale topology) with an isomorphism
$ \mathrm {Spec} A$
(with respect to the étale topology) with an isomorphism
![]() $ F_{\mathcal {P}} \colon (\phi ^*\mathcal {P})[1/I] \overset {\sim }{\to } \mathcal {P}[1/I] $
of G-torsors over
$ F_{\mathcal {P}} \colon (\phi ^*\mathcal {P})[1/I] \overset {\sim }{\to } \mathcal {P}[1/I] $
of G-torsors over
![]() $ \mathrm {Spec} A[1/I]$
. We call
$ \mathrm {Spec} A[1/I]$
. We call
![]() $F_{\mathcal {P}}$
the Frobenius of
$F_{\mathcal {P}}$
the Frobenius of
![]() $\mathcal {P}$
. We say that
$\mathcal {P}$
. We say that
![]() $\mathcal {P}$
is of type
$\mathcal {P}$
is of type
![]() $\mu $
if
$\mu $
if
![]() $(\pi , I)$
-completely étale locally on A, there exists some trivialization
$(\pi , I)$
-completely étale locally on A, there exists some trivialization
![]() $\mathcal {P} \simeq G_A$
under which the isomorphism
$\mathcal {P} \simeq G_A$
under which the isomorphism
![]() $F_{\mathcal {P}}$
is given by
$F_{\mathcal {P}}$
is given by
![]() $g \mapsto Yg$
for an element Y in the double coset
$g \mapsto Yg$
for an element Y in the double coset
where
![]() $d \in I$
is a generator.
$d \in I$
is a generator.
Proposition 2.4.5. There is an equivalence
![]() $\mathcal {Q} \mapsto \mathcal {Q}_{\mathrm {BK}}$
from the groupoid
$\mathcal {Q} \mapsto \mathcal {Q}_{\mathrm {BK}}$
from the groupoid ![]() to the groupoid of G-Breuil–Kisin modules of type
to the groupoid of G-Breuil–Kisin modules of type
![]() $\mu $
over
$\mu $
over
![]() $(A, I)$
. This equivalence is compatible with base change along any map
$(A, I)$
. This equivalence is compatible with base change along any map
![]() $(A, I) \to (A', I')$
.
$(A, I) \to (A', I')$
.
Proof. See [Reference ItoIto23, Proposition 5.3.8]. For the construction of the functor
![]() $\mathcal {Q} \mapsto \mathcal {Q}_{\mathrm {BK}}$
, see [Reference ItoIto23, Definition 5.3.6].
$\mathcal {Q} \mapsto \mathcal {Q}_{\mathrm {BK}}$
, see [Reference ItoIto23, Definition 5.3.6].
Example 2.4.6. Assume that
![]() $(A, I)$
is orientable. Let
$(A, I)$
is orientable. Let
![]() $d \in I$
be a generator. For an element
$d \in I$
be a generator. For an element
![]() $X \in G(A)_I$
, the trivial G-torsor
$X \in G(A)_I$
, the trivial G-torsor
![]() $G_A$
with the isomorphism
$G_A$
with the isomorphism
is a G-Breuil–Kisin module of type
![]() $\mu $
over
$\mu $
over
![]() $(A, I)$
, and this is isomorphic to the one
$(A, I)$
, and this is isomorphic to the one
![]() $(\mathcal {Q}_X)_{\mathrm {BK}}$
associated with
$(\mathcal {Q}_X)_{\mathrm {BK}}$
associated with ![]() .
.
Example 2.4.7 (Minuscule Breuil–Kisin module).
We assume that
![]() $G= {\mathrm {GL}} _N$
. Let
$G= {\mathrm {GL}} _N$
. Let
![]() $\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _{N}$
be the cocharacter defined by
$\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _{N}$
be the cocharacter defined by
 $$\begin{align*}t \mapsto {\mathrm{diag}}{(\underbrace{t, \dotsc, t}_s, \underbrace{1, \dotsc, 1}_{N-s})}, \end{align*}$$
$$\begin{align*}t \mapsto {\mathrm{diag}}{(\underbrace{t, \dotsc, t}_s, \underbrace{1, \dotsc, 1}_{N-s})}, \end{align*}$$
which is 1-bounded. A minuscule Breuil–Kisin module over
![]() $(A, I)$
is a finite projective A-module M together with an A-linear homomorphism
$(A, I)$
is a finite projective A-module M together with an A-linear homomorphism
whose cokernel is killed by I. We set
![]() $ {\mathrm {Fil}} ^1(\phi ^*M):= \{ \, x \in \phi ^*M \, \vert \, F_M(x) \in IM \, \} $
and let
$ {\mathrm {Fil}} ^1(\phi ^*M):= \{ \, x \in \phi ^*M \, \vert \, F_M(x) \in IM \, \} $
and let
![]() $ P^1 \subset (\phi ^*M)/I(\phi ^*M) $
be the image of
$ P^1 \subset (\phi ^*M)/I(\phi ^*M) $
be the image of
![]() $ {\mathrm {Fil}} ^1(\phi ^*M)$
. By [Reference ItoIto23, Proposition 3.1.6], we see that
$ {\mathrm {Fil}} ^1(\phi ^*M)$
. By [Reference ItoIto23, Proposition 3.1.6], we see that
![]() $P^1$
is a direct summand of
$P^1$
is a direct summand of
![]() $(\phi ^*M)/I(\phi ^*M)$
. We say that M is of type
$(\phi ^*M)/I(\phi ^*M)$
. We say that M is of type
![]() $\mu $
if the rank of M (resp.
$\mu $
if the rank of M (resp.
![]() $P^1$
) is constant and equal to N (resp. s). Let
$P^1$
) is constant and equal to N (resp. s). Let
![]() $ \mathrm {BK}_\mu (A, I)^{\simeq } $
be the groupoid of minuscule Breuil–Kisin modules over
$ \mathrm {BK}_\mu (A, I)^{\simeq } $
be the groupoid of minuscule Breuil–Kisin modules over
![]() $(A, I)$
of type
$(A, I)$
of type
![]() $\mu $
. In [Reference ItoIto23, Example 5.3.3, Corollary 5.3.11], we constructed a natural equivalence of groupoids:
$\mu $
. In [Reference ItoIto23, Example 5.3.3, Corollary 5.3.11], we constructed a natural equivalence of groupoids:
We set
![]() $ {\mathrm {Fil}} ^1_\mu := A^s \oplus I^{N-s} \subset A^N$
. Then the underlying
$ {\mathrm {Fil}} ^1_\mu := A^s \oplus I^{N-s} \subset A^N$
. Then the underlying
![]() $G_{\mu , A, I}$
-torsor of
$G_{\mu , A, I}$
-torsor of
![]() $\mathcal {Q}(M)$
is the functor
$\mathcal {Q}(M)$
is the functor
defined by sending
![]() $B \in (A, I)_{\mathrm {\acute {e}t}}$
to the set of isomorphisms
$B \in (A, I)_{\mathrm {\acute {e}t}}$
to the set of isomorphisms
![]() $B^N \overset {\sim }{\to } (\phi ^*M) \otimes _A B$
under which
$B^N \overset {\sim }{\to } (\phi ^*M) \otimes _A B$
under which
![]() $ {\mathrm {Fil}} ^1_\mu $
agrees with
$ {\mathrm {Fil}} ^1_\mu $
agrees with
![]() $ {\mathrm {Fil}} ^1(\phi ^*M)$
.
$ {\mathrm {Fil}} ^1(\phi ^*M)$
.
2.5 Hodge filtrations and G-
 $\phi $
-modules
$\phi $
-modules
Let
![]() $(A, I)$
be an orientable and bounded
$(A, I)$
be an orientable and bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
. Here, we recall the definitions of the Hodge filtration
${\mathcal O}$
. Here, we recall the definitions of the Hodge filtration
![]() $P(\mathcal {Q})_{A/I}$
and the underlying G-
$P(\mathcal {Q})_{A/I}$
and the underlying G-
![]() $\phi $
-module
$\phi $
-module
![]() $\mathcal {Q}_\phi $
of a G-
$\mathcal {Q}_\phi $
of a G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A, I)$
introduced in [Reference ItoIto23].
$(A, I)$
introduced in [Reference ItoIto23].
Let ![]() ,
, ![]() , and
, and ![]() be the sheaves on
be the sheaves on
![]() $(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
defined by
$(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
defined by
respectively. Let ![]() be the inclusion. The composition of
be the inclusion. The composition of
![]() $\tau $
with the projection
$\tau $
with the projection ![]() is denoted by
is denoted by
![]() $\overline {\tau }$
, which factors through a homomorphism
$\overline {\tau }$
, which factors through a homomorphism ![]() by Proposition 2.3.3. We have a commutative diagram
by Proposition 2.3.3. We have a commutative diagram

Remark 2.5.1. For a G-torsor
![]() $\mathcal {P}$
over
$\mathcal {P}$
over
![]() $ \mathrm {Spec} A$
(with respect to the étale topology), the sheaf on
$ \mathrm {Spec} A$
(with respect to the étale topology), the sheaf on
![]() $(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
defined by
$(A, I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
defined by
![]() $B \mapsto \mathcal {P}(B)$
is a
$B \mapsto \mathcal {P}(B)$
is a ![]() -torsor. By [Reference ItoIto23, Proposition 4.3.1], this construction induces an equivalence of categories
-torsor. By [Reference ItoIto23, Proposition 4.3.1], this construction induces an equivalence of categories
We will make no distinction between a G-torsor over
![]() $ \mathrm {Spec} A$
and the corresponding
$ \mathrm {Spec} A$
and the corresponding ![]() -torsor. Similarly, the category of G-torsors over
-torsor. Similarly, the category of G-torsors over
![]() $ \mathrm {Spec} A/I$
(resp.
$ \mathrm {Spec} A/I$
(resp.
![]() $P_\mu $
-torsors over
$P_\mu $
-torsors over
![]() $ \mathrm {Spec} A/I$
) is equivalent to that of
$ \mathrm {Spec} A/I$
) is equivalent to that of ![]() -torsors (resp.
-torsors (resp. ![]() -torsors).
-torsors).
Let ![]() . We write
. We write
for the pushout of
![]() $\mathcal {Q}$
along
$\mathcal {Q}$
along
![]() $\tau $
(resp.
$\tau $
(resp.
![]() $\overline {\tau }$
, resp.
$\overline {\tau }$
, resp.
![]() $\overline {\tau }_P$
).
$\overline {\tau }_P$
).
Definition 2.5.2. We regard
![]() $P(\mathcal {Q})_{A/I}$
as a
$P(\mathcal {Q})_{A/I}$
as a
![]() $P_\mu $
-torsor over
$P_\mu $
-torsor over
![]() $ \mathrm {Spec} A/I$
. We call
$ \mathrm {Spec} A/I$
. We call
![]() $P(\mathcal {Q})_{A/I}$
(or the morphism
$P(\mathcal {Q})_{A/I}$
(or the morphism
![]() $P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
) the Hodge filtration of
$P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
) the Hodge filtration of
![]() $\mathcal {Q}_{A/I}$
. We also say that
$\mathcal {Q}_{A/I}$
. We also say that
![]() $P(\mathcal {Q})_{A/I}$
is the Hodge filtration of
$P(\mathcal {Q})_{A/I}$
is the Hodge filtration of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
We recall the following useful fact:
Proposition 2.5.3. A G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A, I)$
is banal if and only if the Hodge filtration
$(A, I)$
is banal if and only if the Hodge filtration
![]() $P(\mathcal {Q})_{A/I}$
is a trivial
$P(\mathcal {Q})_{A/I}$
is a trivial
![]() $P_{\mu }$
-torsor over
$P_{\mu }$
-torsor over
![]() $ \mathrm {Spec} A/I$
.
$ \mathrm {Spec} A/I$
.
Proof. See [Reference ItoIto23, Proposition 5.4.5].
A G-
![]() $\phi $
-module over
$\phi $
-module over
![]() $(A, I)$
is a G-torsor
$(A, I)$
is a G-torsor
![]() $\mathcal {P}$
over
$\mathcal {P}$
over
![]() $ \mathrm {Spec} A$
with an isomorphism
$ \mathrm {Spec} A$
with an isomorphism
of G-torsors over
![]() $ \mathrm {Spec} A[1/\phi (I)]$
. Here, we set
$ \mathrm {Spec} A[1/\phi (I)]$
. Here, we set
![]() $A[1/\phi (I)]:=A[1/\phi (d)]$
for a generator
$A[1/\phi (I)]:=A[1/\phi (d)]$
for a generator
![]() $d \in I$
. We call
$d \in I$
. We call
![]() $\phi _{\mathcal {P}}$
the Frobenius of
$\phi _{\mathcal {P}}$
the Frobenius of
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
In [Reference ItoIto23, Section 5.5], we constructed a functor
If
![]() $\mathcal {Q}=\mathcal {Q}_X$
is the banal G-
$\mathcal {Q}=\mathcal {Q}_X$
is the banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
associated with an element
$(A, I)$
associated with an element
![]() $X \in G(A)_I$
(see Remark 2.4.2), then the isomorphism
$X \in G(A)_I$
(see Remark 2.4.2), then the isomorphism
![]() $\phi _{\mathcal {Q}_A}$
is defined as follows. We set
$\phi _{\mathcal {Q}_A}$
is defined as follows. We set
which is independent of the choice of a generator
![]() $d \in I$
. (See (2.1) for the notation
$d \in I$
. (See (2.1) for the notation
![]() $X_d$
.) We have
$X_d$
.) We have
![]() $\mathcal {Q}_A=G_A$
, and hence,
$\mathcal {Q}_A=G_A$
, and hence,
![]() $\phi ^*(\mathcal {Q}_A)=G_A$
. The isomorphism
$\phi ^*(\mathcal {Q}_A)=G_A$
. The isomorphism
![]() $\phi _{\mathcal {Q}_A}$
is then given by
$\phi _{\mathcal {Q}_A}$
is then given by
![]() $ g \mapsto X_\phi g. $
$ g \mapsto X_\phi g. $
Definition 2.5.4. The G-
![]() $\phi $
-module
$\phi $
-module
![]() $ \mathcal {Q}_{\phi }=(\mathcal {Q}_A, \phi _{\mathcal {Q}_A}) $
over
$ \mathcal {Q}_{\phi }=(\mathcal {Q}_A, \phi _{\mathcal {Q}_A}) $
over
![]() $(A, I)$
is called the underlying G-
$(A, I)$
is called the underlying G-
![]() $\phi $
-module of
$\phi $
-module of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Example 2.5.5. We retain the notation of Example 2.4.7. Let
![]() $\mathcal {Q}:=\mathcal {Q}(M)$
be the
$\mathcal {Q}:=\mathcal {Q}(M)$
be the
![]() $ {\mathrm {GL}} _N$
-
$ {\mathrm {GL}} _N$
-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
associated with a minuscule Breuil–Kisin module M over
$(A, I)$
associated with a minuscule Breuil–Kisin module M over
![]() $(A, I)$
of type
$(A, I)$
of type
![]() $\mu $
. The underlying
$\mu $
. The underlying
![]() $ {\mathrm {GL}} _N$
-
$ {\mathrm {GL}} _N$
-
![]() $\phi $
-module
$\phi $
-module
![]() $\mathcal {Q}_{\phi }$
is the one naturally associated with the pair
$\mathcal {Q}_{\phi }$
is the one naturally associated with the pair
For the Hodge filtration
![]() $P(\mathcal {Q})_{A/I}$
, we have
$P(\mathcal {Q})_{A/I}$
, we have
where the right-hand side is the scheme of isomorphisms
![]() $f \colon (A/I)^N \overset {\sim }{\to } (\phi ^*M)/I(\phi ^*M)$
such that
$f \colon (A/I)^N \overset {\sim }{\to } (\phi ^*M)/I(\phi ^*M)$
such that
![]() $f((A/I)^s \oplus 0)=P^1$
.
$f((A/I)^s \oplus 0)=P^1$
.
2.6 Prismatic G-
 $\mu $
-displays over complete regular local rings
$\mu $
-displays over complete regular local rings
In this subsection, we recall the main result of [Reference ItoIto23].
Definition 2.6.1. Let R be a
![]() $\pi $
-adically complete
$\pi $
-adically complete
![]() ${\mathcal O}$
-algebra. We define the following groupoid:
${\mathcal O}$
-algebra. We define the following groupoid:
A prismatic G-
![]() $\mu $
-display over R is an object of
$\mu $
-display over R is an object of ![]() .
.
For a homomorphism
![]() $h \colon R \to R'$
of
$h \colon R \to R'$
of
![]() $\pi $
-adically complete
$\pi $
-adically complete
![]() ${\mathcal O}$
-algebras, we have a base change functor
${\mathcal O}$
-algebras, we have a base change functor
Remark 2.6.2. Giving a prismatic G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}$
over R is equivalent to giving a section of the fibered category
$\mathfrak {Q}$
over R is equivalent to giving a section of the fibered category ![]() over
over ![]() . We thus have the associated G-
. We thus have the associated G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}_{(A, I)}$
over
$\mathfrak {Q}_{(A, I)}$
over
![]() $(A, I)$
for each
$(A, I)$
for each ![]() and a natural isomorphism
and a natural isomorphism
for each morphism
![]() $f \colon (A, I) \to (A', I')$
in
$f \colon (A, I) \to (A', I')$
in ![]() . We call
. We call
![]() $\mathfrak {Q}_{(A, I)}$
the value of
$\mathfrak {Q}_{(A, I)}$
the value of
![]() $\mathfrak {Q}$
at
$\mathfrak {Q}$
at ![]() . Recall that an object of
. Recall that an object of ![]() is given by a bounded
is given by a bounded
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $(A, I)$
over
$(A, I)$
over
![]() ${\mathcal O}$
together with a homomorphism
${\mathcal O}$
together with a homomorphism
![]() $g \colon R \to A/I$
over
$g \colon R \to A/I$
over
![]() ${\mathcal O}$
. We also write
${\mathcal O}$
. We also write
![]() $ \mathfrak {Q}_{g}:=\mathfrak {Q}_{(A, I)} $
in order to emphasize that it depends on the homomorphism g. For a homomorphism
$ \mathfrak {Q}_{g}:=\mathfrak {Q}_{(A, I)} $
in order to emphasize that it depends on the homomorphism g. For a homomorphism
![]() $h \colon R \to R'$
and an object
$h \colon R \to R'$
and an object ![]() , we have
, we have
Example 2.6.3. The functor
is an equivalence since ![]() is an initial object ([Reference ItoIto23, Example 2.5.8]).
is an initial object ([Reference ItoIto23, Example 2.5.8]).
Let
![]() $\mathcal {C}_{\mathcal O}$
be the category of complete regular local rings R with a local homomorphism
$\mathcal {C}_{\mathcal O}$
be the category of complete regular local rings R with a local homomorphism
![]() ${\mathcal O} \to R$
which induces an isomorphism on the residue fields. The morphisms in
${\mathcal O} \to R$
which induces an isomorphism on the residue fields. The morphisms in
![]() $\mathcal {C}_{\mathcal O}$
are the local homomorphisms over
$\mathcal {C}_{\mathcal O}$
are the local homomorphisms over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
An important feature of the category
![]() $\mathcal {C}_{\mathcal O}$
is the following:
$\mathcal {C}_{\mathcal O}$
is the following:
Remark 2.6.4. Let
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
be an
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
be an
![]() ${\mathcal O}_E$
-prism of Breuil–Kisin type over
${\mathcal O}_E$
-prism of Breuil–Kisin type over
![]() ${\mathcal O}$
. Then the quotient
${\mathcal O}$
. Then the quotient
![]() $\mathfrak {S}_{\mathcal O}/\mathcal {E}$
belongs to
$\mathfrak {S}_{\mathcal O}/\mathcal {E}$
belongs to
![]() $\mathcal {C}_{\mathcal O}$
. Conversely, any
$\mathcal {C}_{\mathcal O}$
. Conversely, any
![]() $R \in \mathcal {C}_{\mathcal O}$
is of the form
$R \in \mathcal {C}_{\mathcal O}$
is of the form
![]() $ R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E} $
for some
$ R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E} $
for some
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type. (See, for example, [Reference ChengChe18, Section 3.3].)
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type. (See, for example, [Reference ChengChe18, Section 3.3].)
Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. We choose an
$R \in \mathcal {C}_{\mathcal O}$
. We choose an
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type with an isomorphism
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type with an isomorphism
![]() $ R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E} $
over
$ R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E} $
over
![]() ${\mathcal O}$
. The following result is a key ingredient in our deformation theory:
${\mathcal O}$
. The following result is a key ingredient in our deformation theory:
Theorem 2.6.5. The functor
is an equivalence if the cocharacter
![]() $\mu $
is 1-bounded.
$\mu $
is 1-bounded.
Proof. See [Reference ItoIto23, Theorem 6.1.3].
3 The Grothendieck–Messing deformation theory for G-
 $\mu $
-displays
$\mu $
-displays
In this section, we establish an analogue of the Grothendieck–Messing deformation theory for G-
![]() $\mu $
-displays. The contents of this section can be summarized as follows. In Section 3.1, we collect some basic results on deformations of G-
$\mu $
-displays. The contents of this section can be summarized as follows. In Section 3.1, we collect some basic results on deformations of G-
![]() $\mu $
-displays. In Section 3.2, we introduce a class of maps
$\mu $
-displays. In Section 3.2, we introduce a class of maps
![]() $(A', I') \to (A, I)$
of orientable and bounded
$(A', I') \to (A, I)$
of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
, called special nilpotent thickenings, for which we formulate the analogue of the Grothendieck–Messing deformation theory. This class includes the maps
${\mathcal O}$
, called special nilpotent thickenings, for which we formulate the analogue of the Grothendieck–Messing deformation theory. This class includes the maps
![]() $(\mathfrak {S}_{{\mathcal O}, m+1}, (\mathcal {E})) \to (\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E}))$
and
$(\mathfrak {S}_{{\mathcal O}, m+1}, (\mathcal {E})) \to (\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E}))$
and
![]() $(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}, I_S) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
. For a G-
$(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}, I_S) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
. For a G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A, I)$
and its deformation
$(A, I)$
and its deformation
![]() $\mathscr {Q}$
over
$\mathscr {Q}$
over
![]() $(A', I')$
, we construct a period map
$(A', I')$
, we construct a period map
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
from the set
$ {\mathrm {Per}} _{\mathscr {Q}}$
from the set
![]() $ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
of isomorphism classes of deformations of
$ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
of isomorphism classes of deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
to the set of isomorphism classes of lifts of the Hodge filtration
$(A', I')$
to the set of isomorphism classes of lifts of the Hodge filtration
![]() $P(\mathcal {Q})_{A/I}$
in
$P(\mathcal {Q})_{A/I}$
in
![]() $\mathscr {Q}_{A'/I'}$
, and prove that
$\mathscr {Q}_{A'/I'}$
, and prove that
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
is bijective when
$ {\mathrm {Per}} _{\mathscr {Q}}$
is bijective when
![]() $\mu $
is 1-bounded; see Section 3.3 for details. In Section 3.4, under a mild additional assumption on
$\mu $
is 1-bounded; see Section 3.3 for details. In Section 3.4, under a mild additional assumption on
![]() $(A', I') \to (A, I)$
, we show that the set
$(A', I') \to (A, I)$
, we show that the set
![]() $ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
has a natural structure of a torsor under an
$ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
has a natural structure of a torsor under an
![]() $A/I$
-module when
$A/I$
-module when
![]() $\mu $
is 1-bounded. This structure plays an important role in Section 4.
$\mu $
is 1-bounded. This structure plays an important role in Section 4.
3.1 Deformations
Let
![]() $f \colon (A', I') \to (A, I)$
be a map of orientable and bounded
$f \colon (A', I') \to (A, I)$
be a map of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $f \colon A' \to A$
is surjective.
$f \colon A' \to A$
is surjective.
We can define a deformation of a G-
![]() $\mu $
-display in the usual way:
$\mu $
-display in the usual way:
Definition 3.1.1. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
.
$(A, I)$
.
-
(1) A deformation of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(A', I')$
is a pair
$(A', I')$
is a pair
 $ (\mathscr {Q}, h) $
consisting of a G-
$ (\mathscr {Q}, h) $
consisting of a G-
 $\mu $
-display
$\mu $
-display
 $\mathscr {Q}$
over
$\mathscr {Q}$
over
 $(A', I')$
and an isomorphism
$(A', I')$
and an isomorphism
 $ h \colon f^*\mathscr {Q} \overset {\sim }{\to } \mathcal {Q} $
of G-
$ h \colon f^*\mathscr {Q} \overset {\sim }{\to } \mathcal {Q} $
of G-
 $\mu $
-displays over
$\mu $
-displays over
 $(A, I)$
. If there is no ambiguity, we simply write
$(A, I)$
. If there is no ambiguity, we simply write
 $\mathscr {Q}$
instead of
$\mathscr {Q}$
instead of
 $(\mathscr {Q}, h)$
.
$(\mathscr {Q}, h)$
. -
(2) An isomorphism
 $ g \colon (\mathscr {Q}, h) \overset {\sim }{\to } (\mathscr {R}, i) $
of deformations of
$ g \colon (\mathscr {Q}, h) \overset {\sim }{\to } (\mathscr {R}, i) $
of deformations of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(A', I')$
is an isomorphism
$(A', I')$
is an isomorphism
 $g \colon \mathscr {Q} \overset {\sim }{\to } \mathscr {R}$
of G-
$g \colon \mathscr {Q} \overset {\sim }{\to } \mathscr {R}$
of G-
 $\mu $
-display over
$\mu $
-display over
 $(A', I')$
such that
$(A', I')$
such that
 $i \circ (f^*g)=h$
.
$i \circ (f^*g)=h$
.
The set of isomorphism classes of deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
is denoted by
$(A', I')$
is denoted by
The groupoid of deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
is denoted by
$(A', I')$
is denoted by
![]() $ \mathbf {Def}(\mathcal {Q})_{(A', I')}, $
using boldface letters.
$ \mathbf {Def}(\mathcal {Q})_{(A', I')}, $
using boldface letters.
We collect some preliminary results on deformations which will be used in the sequel. Let
![]() $J \subset A'$
(resp.
$J \subset A'$
(resp.
![]() $K \subset A'/I'$
) be the kernel of
$K \subset A'/I'$
) be the kernel of
![]() $A' \to A$
(resp.
$A' \to A$
(resp.
![]() $A'/I' \to A/I$
).
$A'/I' \to A/I$
).
We first note the following fact:
Lemma 3.1.2. Assume that
![]() $A'/I'$
is K-adically complete. Let
$A'/I'$
is K-adically complete. Let
![]() $\mathcal {Q}$
be a banal G-
$\mathcal {Q}$
be a banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
. Then any deformation
$(A, I)$
. Then any deformation
![]() $\mathscr {Q}$
of
$\mathscr {Q}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
is banal.
$(A', I')$
is banal.
Proof. By Proposition 2.5.3, it suffices to prove that the Hodge filtration
![]() $P(\mathscr {Q})_{A'/I'}$
is trivial as a
$P(\mathscr {Q})_{A'/I'}$
is trivial as a
![]() $P_\mu $
-torsor over
$P_\mu $
-torsor over
![]() $ \mathrm {Spec} A'/I'$
. The base change
$ \mathrm {Spec} A'/I'$
. The base change
![]() $P(\mathscr {Q})_{A'/I'} \times _{ \mathrm {Spec} A'/I'} \mathrm {Spec} A/I$
is trivial since
$P(\mathscr {Q})_{A'/I'} \times _{ \mathrm {Spec} A'/I'} \mathrm {Spec} A/I$
is trivial since
![]() $\mathcal {Q}$
is banal. Since
$\mathcal {Q}$
is banal. Since
![]() $P(\mathscr {Q})_{A'/I'}$
is smooth over
$P(\mathscr {Q})_{A'/I'}$
is smooth over
![]() $ \mathrm {Spec} A'/I'$
and
$ \mathrm {Spec} A'/I'$
and
![]() $A'/I'$
is K-adically complete, we see that
$A'/I'$
is K-adically complete, we see that
![]() $P(\mathscr {Q})_{A'/I'}$
is trivial, as desired.
$P(\mathscr {Q})_{A'/I'}$
is trivial, as desired.
The next lemma is an analogue of [Reference LauLau21, Lemma 7.1.4 (b)].
Lemma 3.1.3. If
![]() $A'$
is J-adically complete, then the homomorphism
$A'$
is J-adically complete, then the homomorphism
![]() $f \colon G_\mu (A', I') \to G_\mu (A, I)$
is surjective.
$f \colon G_\mu (A', I') \to G_\mu (A, I)$
is surjective.
Proof. Since
![]() $A'$
is J-adically complete and
$A'$
is J-adically complete and
![]() $P_\mu $
is smooth, the homomorphism
$P_\mu $
is smooth, the homomorphism
![]() $P_\mu (A') \to P_\mu (A)$
is surjective. It is easy to show that
$P_\mu (A') \to P_\mu (A)$
is surjective. It is easy to show that
![]() $U^{-}_{\mu }(A') \cap G_\mu (A', I') \to U^{-}_{\mu }(A) \cap G_\mu (A, I)$
is surjective; see [Reference ItoIto23, Remark 4.2.7]. The claim then follows from Proposition 2.3.3.
$U^{-}_{\mu }(A') \cap G_\mu (A', I') \to U^{-}_{\mu }(A) \cap G_\mu (A, I)$
is surjective; see [Reference ItoIto23, Remark 4.2.7]. The claim then follows from Proposition 2.3.3.
We have the following useful description of deformations for banal G-
![]() $\mu $
-displays.
$\mu $
-displays.
Proposition 3.1.4. Assume that
![]() $A'$
is J-adically complete and
$A'$
is J-adically complete and
![]() $A'/I'$
is K-adically complete. Let
$A'/I'$
is K-adically complete. Let
![]() $X \in G(A)_I$
be an element and
$X \in G(A)_I$
be an element and
![]() $\mathcal {Q}_X$
the banal G-
$\mathcal {Q}_X$
the banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
associated with X. Let
$(A, I)$
associated with X. Let
be the groupoid whose objects are the elements
![]() $Y \in G(A')_{I'}$
such that
$Y \in G(A')_{I'}$
such that
![]() $f(Y)=X$
, and whose morphisms are given by
$f(Y)=X$
, and whose morphisms are given by
For each
![]() $Y \in \mathbf {Def}(X)_{(A', I')}$
, we have a natural isomorphism
$Y \in \mathbf {Def}(X)_{(A', I')}$
, we have a natural isomorphism
![]() $f^*(\mathcal {Q}_Y) \overset {\sim }{\to } \mathcal {Q}_X$
given by
$f^*(\mathcal {Q}_Y) \overset {\sim }{\to } \mathcal {Q}_X$
given by
![]() $1 \in G_{\mu }(A, I)$
. The construction
$1 \in G_{\mu }(A, I)$
. The construction
![]() $Y \mapsto (\mathcal {Q}_Y, 1)$
gives an equivalence
$Y \mapsto (\mathcal {Q}_Y, 1)$
gives an equivalence
Proof. For the map
![]() $f \colon G(A')_{I'} \to G(A)_I$
, see Remark 2.4.3. It is clear that
$f \colon G(A')_{I'} \to G(A)_I$
, see Remark 2.4.3. It is clear that
![]() $Y \mapsto (\mathcal {Q}_Y, 1)$
gives a fully faithful functor. We shall prove that this functor is essentially surjective. Let
$Y \mapsto (\mathcal {Q}_Y, 1)$
gives a fully faithful functor. We shall prove that this functor is essentially surjective. Let
![]() $ (\mathscr {Q}, h) \in \mathbf {Def}(\mathcal {Q}_X)_{(A', I')}. $
It follows from Lemma 3.1.2 that
$ (\mathscr {Q}, h) \in \mathbf {Def}(\mathcal {Q}_X)_{(A', I')}. $
It follows from Lemma 3.1.2 that
![]() $\mathscr {Q}$
is banal. We can identify
$\mathscr {Q}$
is banal. We can identify
![]() $\mathscr {Q}$
with
$\mathscr {Q}$
with
![]() $\mathcal {Q}_Y$
for some
$\mathcal {Q}_Y$
for some
![]() $Y \in G(A')_{I'}$
, and then h is an element of
$Y \in G(A')_{I'}$
, and then h is an element of
![]() $G_{\mu }(A, I)$
satisfying the equality
$G_{\mu }(A, I)$
satisfying the equality
![]() $ X\cdot h=f(Y). $
By Lemma 3.1.3, there exists an element
$ X\cdot h=f(Y). $
By Lemma 3.1.3, there exists an element
![]() $h' \in G_\mu (A', I')$
with
$h' \in G_\mu (A', I')$
with
![]() $f(h')=h$
. We define
$f(h')=h$
. We define
![]() $Y':=Y \cdot (h')^{-1} \in G(A')_{I'}$
. Then
$Y':=Y \cdot (h')^{-1} \in G(A')_{I'}$
. Then
![]() $Y' \in \mathbf {Def}(X)_{(A', I')}$
and
$Y' \in \mathbf {Def}(X)_{(A', I')}$
and
![]() $h'$
induces
$h'$
induces
![]() $ (\mathcal {Q}_Y, h) \overset {\sim }{\to } (\mathcal {Q}_{Y'}, 1). $
$ (\mathcal {Q}_Y, h) \overset {\sim }{\to } (\mathcal {Q}_{Y'}, 1). $
For later use, we also record the following result.
Proposition 3.1.5. Let
![]() $(A, I)$
be an orientable and bounded
$(A, I)$
be an orientable and bounded
![]() ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $J \subset A$
be an ideal satisfying the following conditions:
$J \subset A$
be an ideal satisfying the following conditions:
-
(a) A is J-adically complete.
-
(b) J is stable under
 $\delta _E$
. In particular,
$\delta _E$
. In particular,
 $A/J^m$
admits a
$A/J^m$
admits a
 $\delta _E$
-structure that is compatible with the one on A for every
$\delta _E$
-structure that is compatible with the one on A for every
 $m \geq 1$
.
$m \geq 1$
. -
(c) For every
 $m \geq 1$
, the pair
$m \geq 1$
, the pair
 $(A/J^m, I)$
is an orientable and bounded
$(A/J^m, I)$
is an orientable and bounded
 ${\mathcal O}_E$
-prism over
${\mathcal O}_E$
-prism over
 ${\mathcal O}$
. Here, we abuse notation and denote the image of I in
${\mathcal O}$
. Here, we abuse notation and denote the image of I in
 $A/J^m$
by the same symbol.
$A/J^m$
by the same symbol.
Then the following assertions hold:
-
(1) We have the following equivalence of groupoids:

-
(2) We further assume that for any G-
 $\mu $
-display
$\mu $
-display
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(A, I)$
(resp.
$(A, I)$
(resp.
 $(A/J, I)$
), there is a finite étale covering
$(A/J, I)$
), there is a finite étale covering
 $A \to B$
such that the base change of
$A \to B$
such that the base change of
 $\mathcal {Q}$
to
$\mathcal {Q}$
to
 $(B, IB)$
(resp.
$(B, IB)$
(resp.
 $(B/JB, I(B/JB))$
) is banal. Then we have
$(B/JB, I(B/JB))$
) is banal. Then we have 
Proof. (1) We claim that
Indeed, the first equality is clear since G is affine. The second equality follows from Proposition 2.3.3 (2).
In order to prove (1), it suffices to show that the natural functor
is an equivalence (cf. Remark 2.4.2). The fully faithfulness follows from (3.1). We shall prove that the functor is essentially surjective. An object of
![]() $\mathcal {C}$
can be identified with a family of objects
$\mathcal {C}$
can be identified with a family of objects
![]() $\{ X_m \}_{m \geq 1}$
, where
$\{ X_m \}_{m \geq 1}$
, where
![]() $X_m \in G(A/J^m)_I$
, together with a family of isomorphisms
$X_m \in G(A/J^m)_I$
, together with a family of isomorphisms
![]() $\{ g_m \}_{m \geq 1}$
, where
$\{ g_m \}_{m \geq 1}$
, where
![]() $g_m \in G_\mu (A/J^m, I)$
is such that the equality
$g_m \in G_\mu (A/J^m, I)$
is such that the equality
![]() $X_m\cdot g_m=X_{m+1}$
holds in
$X_m\cdot g_m=X_{m+1}$
holds in
![]() $G(A/J^m)_I$
. Applying Proposition 3.1.4 to the natural map
$G(A/J^m)_I$
. Applying Proposition 3.1.4 to the natural map
![]() $p_m \colon (A/J^{m+1}, I) \to (A/J^{m}, I)$
repeatedly, we can find an element
$p_m \colon (A/J^{m+1}, I) \to (A/J^{m}, I)$
repeatedly, we can find an element
![]() $(X^{\prime }_m)_{m \geq 1} \in \varprojlim _{m} G(A/J^m)_I$
such that the corresponding object of
$(X^{\prime }_m)_{m \geq 1} \in \varprojlim _{m} G(A/J^m)_I$
such that the corresponding object of
![]() $\mathcal {C}$
is isomorphic to the object
$\mathcal {C}$
is isomorphic to the object
![]() $\{ X_m \}_{m \geq 1}$
. Let
$\{ X_m \}_{m \geq 1}$
. Let
![]() $X \in G(A)_I$
be the element corresponding to
$X \in G(A)_I$
be the element corresponding to
![]() $(X^{\prime }_m)_{m \geq 1}$
. Then the image of X under the above functor is isomorphic to the object
$(X^{\prime }_m)_{m \geq 1}$
. Then the image of X under the above functor is isomorphic to the object
![]() $\{ X_m \}_{m \geq 1}$
.
$\{ X_m \}_{m \geq 1}$
.
(2) An object of ![]() can be identified with a family
can be identified with a family
![]() $\{ \mathcal {Q}_m \}_{m \geq 1}$
, where
$\{ \mathcal {Q}_m \}_{m \geq 1}$
, where
![]() $\mathcal {Q}_m$
is a G-
$\mathcal {Q}_m$
is a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A/J^m, I)$
, together with isomorphisms
$(A/J^m, I)$
, together with isomorphisms
![]() $p^*_m(\mathcal {Q}_{m+1}) \overset {\sim }{\to } \mathcal {Q}_{m}$
(
$p^*_m(\mathcal {Q}_{m+1}) \overset {\sim }{\to } \mathcal {Q}_{m}$
(
![]() $m \geq 1$
). Our assumption and Lemma 3.1.2 imply that there is a finite étale covering
$m \geq 1$
). Our assumption and Lemma 3.1.2 imply that there is a finite étale covering
![]() $A \to B$
such that for any
$A \to B$
such that for any
![]() $m \geq 1$
, the base change of
$m \geq 1$
, the base change of
![]() $\mathcal {Q}_m$
to
$\mathcal {Q}_m$
to
![]() $(B/J^mB, I(B/J^mB))$
is banal. We note that for a finite étale covering
$(B/J^mB, I(B/J^mB))$
is banal. We note that for a finite étale covering
![]() $A \to B$
, the ideal
$A \to B$
, the ideal
![]() $JB$
satisfies the above conditions (a), (b), (c). Using these observations and finite étale descent for G-
$JB$
satisfies the above conditions (a), (b), (c). Using these observations and finite étale descent for G-
![]() $\mu $
-displays, we see that (2) follows from (1).
$\mu $
-displays, we see that (2) follows from (1).
Example 3.1.6. Let
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
be an
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
be an
![]() ${\mathcal O}_E$
-prism of Breuil–Kisin type as in Example 2.1.1, where
${\mathcal O}_E$
-prism of Breuil–Kisin type as in Example 2.1.1, where
![]() $\mathfrak {S}_{\mathcal O}={\mathcal O}[[t_1, \dotsc , t_n]]$
. Let
$\mathfrak {S}_{\mathcal O}={\mathcal O}[[t_1, \dotsc , t_n]]$
. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
. By Proposition 2.5.3, there is a finite extension
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
. By Proposition 2.5.3, there is a finite extension
![]() $\widetilde {k}$
of k such that the base change of
$\widetilde {k}$
of k such that the base change of
![]() $\mathcal {Q}$
to
$\mathcal {Q}$
to
![]() $(\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E}))$
is banal, where
$(\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E}))$
is banal, where
![]() $\widetilde {{\mathcal O}}:= W(\widetilde {k}) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E$
and
$\widetilde {{\mathcal O}}:= W(\widetilde {k}) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E$
and
![]() $\mathfrak {S}_{\widetilde {{\mathcal O}}}:=\mathfrak {S}_{\mathcal O} \otimes _{\mathcal O} \widetilde {{\mathcal O}} = \widetilde {{\mathcal O}}[[t_1, \dotsc , t_n]]$
. Therefore, by Proposition 3.1.5, we have
$\mathfrak {S}_{\widetilde {{\mathcal O}}}:=\mathfrak {S}_{\mathcal O} \otimes _{\mathcal O} \widetilde {{\mathcal O}} = \widetilde {{\mathcal O}}[[t_1, \dotsc , t_n]]$
. Therefore, by Proposition 3.1.5, we have
where
![]() $\mathfrak {S}_{{\mathcal O}, m}={\mathcal O}[[t_1, \dotsc , t_n]]/(t_1, \dotsc , t_n)^m$
.
$\mathfrak {S}_{{\mathcal O}, m}={\mathcal O}[[t_1, \dotsc , t_n]]/(t_1, \dotsc , t_n)^m$
.
3.2 Special nilpotent thickenings
Let
![]() $f \colon (A', I') \to (A, I)$
be a map of orientable and bounded
$f \colon (A', I') \to (A, I)$
be a map of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $f \colon A' \to A$
is surjective. Let
$f \colon A' \to A$
is surjective. Let
![]() $J \subset A'$
be the kernel of f. We assume that
$J \subset A'$
be the kernel of f. We assume that
![]() $J^n=0$
for some
$J^n=0$
for some
![]() $n \geq 1$
. In this case, we say that f is a nilpotent thickening. The functor
$n \geq 1$
. In this case, we say that f is a nilpotent thickening. The functor
where B is the
![]() $(\pi , I)$
-adic completion of
$(\pi , I)$
-adic completion of
![]() $B' \otimes _{A'} A$
, is an equivalence (see [Reference ItoIto23, Lemma 2.5.9] for example).
$B' \otimes _{A'} A$
, is an equivalence (see [Reference ItoIto23, Lemma 2.5.9] for example).
Lemma 3.2.1. Let the notation be as above. Then the induced homomorphism
![]() $f_B \colon B' \to B$
is surjective, and we have
$f_B \colon B' \to B$
is surjective, and we have
![]() $J^n_B=0$
for the kernel
$J^n_B=0$
for the kernel
![]() $J_B$
of
$J_B$
of
![]() $f_B$
. If furthermore
$f_B$
. If furthermore
![]() $\phi _{A'}(J) = 0$
, then
$\phi _{A'}(J) = 0$
, then
![]() $\phi _{B'}(J_B) = 0$
.
$\phi _{B'}(J_B) = 0$
.
Proof. We have the following exact sequence for every
![]() $m \geq 1$
:
$m \geq 1$
:
Since
![]() $A'/(\pi , I')^m \to B'/(\pi , I')^m$
is flat, the induced sequence
$A'/(\pi , I')^m \to B'/(\pi , I')^m$
is flat, the induced sequence
is also exact. By taking the limit over m, we see that
![]() $B' \to B$
is surjective, and
$B' \to B$
is surjective, and
Using this isomorphism, we see that
![]() $J^n_B=0$
, and that
$J^n_B=0$
, and that
![]() $\phi _{B'}(J_B) = 0$
if
$\phi _{B'}(J_B) = 0$
if
![]() $\phi _{A'}(J) =0$
.
$\phi _{A'}(J) =0$
.
Definition 3.2.2 (Special nilpotent thickening).
Let
![]() $ f \colon (A', I') \to (A, I) $
be a nilpotent thickening of orientable and bounded
$ f \colon (A', I') \to (A, I) $
be a nilpotent thickening of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $J \subset A'$
be the kernel of
$J \subset A'$
be the kernel of
![]() $f \colon A' \to A$
. We say that f is a special nilpotent thickening if it satisfies the following two conditions:
$f \colon A' \to A$
. We say that f is a special nilpotent thickening if it satisfies the following two conditions:
-
(1) We have
 $\phi _{A'}(J) = 0$
.
$\phi _{A'}(J) = 0$
. -
(2) Let
 $d \in I'$
be a generator. For any
$d \in I'$
be a generator. For any
 $(\pi , I')$
-completely étale
$(\pi , I')$
-completely étale
 $A'$
-algebra
$A'$
-algebra
 $B'$
, the element
$B'$
, the element
 $\phi _{B'}(d)$
is a nonzerodivisor in
$\phi _{B'}(d)$
is a nonzerodivisor in
 $B'$
.
$B'$
.
Remark 3.2.3. It follows from Lemma 3.2.1 that if
![]() $f \colon (A', I') \to (A, I)$
is a nilpotent thickening (resp. a special nilpotent thickening), then for any
$f \colon (A', I') \to (A, I)$
is a nilpotent thickening (resp. a special nilpotent thickening), then for any
![]() $B' \in (A', I')_{\mathrm {\acute {e}t}}$
with corresponding
$B' \in (A', I')_{\mathrm {\acute {e}t}}$
with corresponding
![]() $B \in (A, I)_{\mathrm {\acute {e}t}}$
, the induced map
$B \in (A, I)_{\mathrm {\acute {e}t}}$
, the induced map
![]() $(B', I'B') \to (B, IB)$
is also a nilpotent thickening (resp. a special nilpotent thickening).
$(B', I'B') \to (B, IB)$
is also a nilpotent thickening (resp. a special nilpotent thickening).
Example 3.2.4. If
![]() $(A, I)$
is either
$(A, I)$
is either
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
or
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
or
![]() $(\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E}))$
as in Example 2.1.1, then
$(\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E}))$
as in Example 2.1.1, then
![]() $(A, I)$
satisfies the condition (2) in Definition 3.2.2. Indeed, it is clear that
$(A, I)$
satisfies the condition (2) in Definition 3.2.2. Indeed, it is clear that
![]() $\phi (\mathcal {E})$
is a nonzerodivisor in A. Since A is noetherian, any
$\phi (\mathcal {E})$
is a nonzerodivisor in A. Since A is noetherian, any
![]() $(\pi , I)$
-completely étale A-algebra B is flat over A, which in turn implies that
$(\pi , I)$
-completely étale A-algebra B is flat over A, which in turn implies that
![]() $\phi (\mathcal {E})$
is a nonzerodivisor in B.
$\phi (\mathcal {E})$
is a nonzerodivisor in B.
Example 3.2.5. Let
![]() $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
![]() ${\mathcal O}$
(see Definition 2.1.4). Then the
${\mathcal O}$
(see Definition 2.1.4). Then the
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $ (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
as in Proposition 2.1.3 satisfies the condition (2) in Definition 3.2.2. Indeed, by Lemma 2.2.3, it suffices to show that
$ (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
as in Proposition 2.1.3 satisfies the condition (2) in Definition 3.2.2. Indeed, by Lemma 2.2.3, it suffices to show that
![]() $\phi (\xi )$
is a nonzerodivisor in
$\phi (\xi )$
is a nonzerodivisor in
![]() $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
. Since
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
. Since
![]() $ \phi \colon W_{{\mathcal O}_E}(S^\flat )/[(a^\flat )^{1/q}]^m \to W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m $
is bijective and
$ \phi \colon W_{{\mathcal O}_E}(S^\flat )/[(a^\flat )^{1/q}]^m \to W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m $
is bijective and
![]() $\xi $
is a nonzerodivisor in
$\xi $
is a nonzerodivisor in
![]() $W_{{\mathcal O}_E}(S^\flat )/[(a^\flat )^{1/q}]^m$
(by Proposition 2.1.3), the assertion follows.
$W_{{\mathcal O}_E}(S^\flat )/[(a^\flat )^{1/q}]^m$
(by Proposition 2.1.3), the assertion follows.
Example 3.2.6. Let the notation be as in Example 3.2.4 and Example 3.2.5. In this paper, we say that a nilpotent thickening
![]() $f \colon (A', I') \to (A, I)$
is of Breuil–Kisin type (resp. of perfectoid type) if it is of the form
$f \colon (A', I') \to (A, I)$
is of Breuil–Kisin type (resp. of perfectoid type) if it is of the form
 $$ \begin{align*} (\mathfrak{S}_{{\mathcal O}, m+1}, (\mathcal{E})) &\to (\mathfrak{S}_{{\mathcal O}, m}, (\mathcal{E})) \\ (\text{resp.\ } (W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m+1}, I_S) &\to (W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m}, I_S)). \end{align*} $$
$$ \begin{align*} (\mathfrak{S}_{{\mathcal O}, m+1}, (\mathcal{E})) &\to (\mathfrak{S}_{{\mathcal O}, m}, (\mathcal{E})) \\ (\text{resp.\ } (W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m+1}, I_S) &\to (W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m}, I_S)). \end{align*} $$
In either case, f is a special nilpotent thickening.
Deformations of G-
![]() $\phi $
-modules are defined in the usual way. If
$\phi $
-modules are defined in the usual way. If
![]() $\mathcal {Q}$
is a G-
$\mathcal {Q}$
is a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
and
$(A, I)$
and
![]() $\mathscr {Q}$
is a deformation of
$\mathscr {Q}$
is a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
, then
$(A', I')$
, then
![]() $\mathscr {Q}_\phi $
is naturally a deformation of
$\mathscr {Q}_\phi $
is naturally a deformation of
![]() $\mathcal {Q}_\phi $
over
$\mathcal {Q}_\phi $
over
![]() $(A', I')$
. Here,
$(A', I')$
. Here,
![]() $\mathscr {Q}_\phi $
and
$\mathscr {Q}_\phi $
and
![]() $\mathcal {Q}_\phi $
are the underlying G-
$\mathcal {Q}_\phi $
are the underlying G-
![]() $\phi $
-modules; see Definition 2.5.4. The following proposition is the key ingredient in the construction of period maps introduced in Section 3.3 below.
$\phi $
-modules; see Definition 2.5.4. The following proposition is the key ingredient in the construction of period maps introduced in Section 3.3 below.
Proposition 3.2.7. Assume that
![]() $f \colon (A', I') \to (A, I)$
is a special nilpotent thickening. Let
$f \colon (A', I') \to (A, I)$
is a special nilpotent thickening. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
. Let
$(A, I)$
. Let
![]() $(\mathscr {Q}, h)$
and
$(\mathscr {Q}, h)$
and
![]() $(\mathscr {R}, i)$
be two deformations of
$(\mathscr {R}, i)$
be two deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
. Then the following assertions hold:
$(A', I')$
. Then the following assertions hold:
-
(1) There exists a unique isomorphism
 $ \psi \colon \mathscr {Q}_{\phi } \overset {\sim }{\to } \mathscr {R}_{\phi } $
of deformations of
$ \psi \colon \mathscr {Q}_{\phi } \overset {\sim }{\to } \mathscr {R}_{\phi } $
of deformations of
 $\mathcal {Q}_{\phi }$
over
$\mathcal {Q}_{\phi }$
over
 $(A', I')$
.
$(A', I')$
. -
(2) There is at most one isomorphism between two deformations
 $(\mathscr {Q}, h)$
and
$(\mathscr {Q}, h)$
and
 $(\mathscr {R}, i)$
.
$(\mathscr {R}, i)$
.
Proof. (1) The problem is
![]() $(\pi , I)$
-completely étale local on A by
$(\pi , I)$
-completely étale local on A by
![]() $(\pi , I)$
-completely étale descent for G-
$(\pi , I)$
-completely étale descent for G-
![]() $\phi $
-modules (which follows from the same argument as in [Reference ItoIto23, Remark 5.1.3]) and the uniqueness assertion. Thus, we may assume that
$\phi $
-modules (which follows from the same argument as in [Reference ItoIto23, Remark 5.1.3]) and the uniqueness assertion. Thus, we may assume that
![]() $\mathscr {Q}$
,
$\mathscr {Q}$
,
![]() $\mathscr {R}$
and
$\mathscr {R}$
and
![]() $\mathcal {Q}$
are banal. We can identify
$\mathcal {Q}$
are banal. We can identify
![]() $\mathcal {Q}$
with
$\mathcal {Q}$
with
![]() $\mathcal {Q}_X$
for some
$\mathcal {Q}_X$
for some
![]() $X \in G(A)_I$
. By Proposition 3.1.4, we may assume that
$X \in G(A)_I$
. By Proposition 3.1.4, we may assume that
![]() $(\mathscr {Q}, h)$
and
$(\mathscr {Q}, h)$
and
![]() $(\mathscr {R}, i)$
are of the form
$(\mathscr {R}, i)$
are of the form
![]() $(\mathcal {Q}_Y, 1)$
and
$(\mathcal {Q}_Y, 1)$
and
![]() $(\mathcal {Q}_Z, 1)$
, respectively, for some
$(\mathcal {Q}_Z, 1)$
, respectively, for some
![]() $Y, Z \in \mathbf {Def}(X)_{(A', I')}$
. It suffices to prove that there exists a unique element
$Y, Z \in \mathbf {Def}(X)_{(A', I')}$
. It suffices to prove that there exists a unique element
![]() $\psi \in G(A')$
such that
$\psi \in G(A')$
such that
![]() $f(\psi )=1$
in
$f(\psi )=1$
in
![]() $G(A)$
and
$G(A)$
and
Here,
![]() $Y_\phi , Z_\phi \in G(A'[1/\phi (I')])$
are the elements defined in (2.2).
$Y_\phi , Z_\phi \in G(A'[1/\phi (I')])$
are the elements defined in (2.2).
We fix a generator
![]() $d \in I'$
. We shall show that the element
$d \in I'$
. We shall show that the element
satisfies
![]() $f(\psi )=1$
and (3.2). Indeed, since
$f(\psi )=1$
and (3.2). Indeed, since
![]() $X=f(Y)=f(Z)$
, we have
$X=f(Y)=f(Z)$
, we have
![]() $f(\psi )=1$
. This implies that
$f(\psi )=1$
. This implies that
![]() $f(\mu (d)\psi \mu (d)^{-1})=1$
. By our assumption that
$f(\mu (d)\psi \mu (d)^{-1})=1$
. By our assumption that
![]() $\phi _{A'}(J)=0$
for the kernel
$\phi _{A'}(J)=0$
for the kernel
![]() $J \subset A'$
of
$J \subset A'$
of
![]() $f \colon A' \to A$
, it then follows that
$f \colon A' \to A$
, it then follows that
![]() $\phi (\mu (d)\psi \mu (d)^{-1})=1$
, whence (3.2) holds.
$\phi (\mu (d)\psi \mu (d)^{-1})=1$
, whence (3.2) holds.
It remains to show the uniqueness of
![]() $\psi $
. Let
$\psi $
. Let
![]() $\psi \in G(A')$
be an element satisfying
$\psi \in G(A')$
be an element satisfying
![]() $f(\psi )=1$
and (3.2). As explained above, the equality
$f(\psi )=1$
and (3.2). As explained above, the equality
![]() $f(\psi )=1$
implies
$f(\psi )=1$
implies
![]() $\phi (\mu (d)\psi \mu (d)^{-1})=1$
. Then it follows from (3.2) that
$\phi (\mu (d)\psi \mu (d)^{-1})=1$
. Then it follows from (3.2) that
![]() $\psi =Z_d(Y_d)^{-1}$
in
$\psi =Z_d(Y_d)^{-1}$
in
![]() $G(A'[1/\phi (I')])$
. Since the natural homomorphism
$G(A'[1/\phi (I')])$
. Since the natural homomorphism
![]() $G(A') \to G(A'[1/\phi (I')])$
is injective by the condition (2) in Definition 3.2.2, we conclude that
$G(A') \to G(A'[1/\phi (I')])$
is injective by the condition (2) in Definition 3.2.2, we conclude that
![]() $\psi =Z_d(Y_d)^{-1}$
in
$\psi =Z_d(Y_d)^{-1}$
in
![]() $G(A')$
.
$G(A')$
.
(2) We note that the functor
![]() $\mathcal {Q} \mapsto \mathcal {Q}_{\phi }$
from
$\mathcal {Q} \mapsto \mathcal {Q}_{\phi }$
from ![]() to the groupoid of G-
to the groupoid of G-
![]() $\phi $
-modules over
$\phi $
-modules over
![]() $(A, I)$
is faithful (since the functor from the groupoid of
$(A, I)$
is faithful (since the functor from the groupoid of
![]() $G_{\mu , A, I}$
-torsors to that of
$G_{\mu , A, I}$
-torsors to that of ![]() -torsors obtained by pushout along the inclusion
-torsors obtained by pushout along the inclusion ![]() is faithful). Then (2) follows from the uniqueness assertion in (1).
is faithful). Then (2) follows from the uniqueness assertion in (1).
Remark 3.2.8. Let the notation be as in Proposition 3.1.4. Let
![]() $Y, Z \in \mathbf {Def}(X)_{(A', I')}$
. For the deformations
$Y, Z \in \mathbf {Def}(X)_{(A', I')}$
. For the deformations
![]() $(\mathcal {Q}_Y, 1)$
and
$(\mathcal {Q}_Y, 1)$
and
![]() $(\mathcal {Q}_Z, 1)$
of the G-
$(\mathcal {Q}_Z, 1)$
of the G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}_X$
, the proof of Proposition 3.2.7 shows that for any generator
$\mathcal {Q}_X$
, the proof of Proposition 3.2.7 shows that for any generator
![]() $d \in I'$
,
$d \in I'$
,
If this is the case, the unique isomorphism
![]() $(\mathcal {Q}_Y, 1) \overset {\sim }{\to } (\mathcal {Q}_Z, 1)$
is given by
$(\mathcal {Q}_Y, 1) \overset {\sim }{\to } (\mathcal {Q}_Z, 1)$
is given by
![]() $Z_d(Y_d)^{-1}$
.
$Z_d(Y_d)^{-1}$
.
Corollary 3.2.9. Assume that
![]() $f \colon (A', I') \to (A, I)$
is a special nilpotent thickening. Let
$f \colon (A', I') \to (A, I)$
is a special nilpotent thickening. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
. For each
$(A, I)$
. For each
![]() $B' \in (A', I')_{\mathrm {\acute {e}t}}$
with corresponding
$B' \in (A', I')_{\mathrm {\acute {e}t}}$
with corresponding
![]() $B \in (A, I)_{\mathrm {\acute {e}t}}$
, we denote the base change of
$B \in (A, I)_{\mathrm {\acute {e}t}}$
, we denote the base change of
![]() $\mathcal {Q}$
to
$\mathcal {Q}$
to
![]() $(B, IB)$
by
$(B, IB)$
by
![]() $\mathcal {Q}_{(B, IB)}$
. Then the functor
$\mathcal {Q}_{(B, IB)}$
. Then the functor
forms a sheaf with respect to the
![]() $(\pi , I')$
-completely étale topology.
$(\pi , I')$
-completely étale topology.
Proof. This is an immediate consequence of Proposition 3.2.7 (2) and
![]() $(\pi , I)$
-completely étale descent for G-
$(\pi , I)$
-completely étale descent for G-
![]() $\mu $
-displays.
$\mu $
-displays.
Corollary 3.2.10. Let the notation be as in Example 3.2.4 and Example 3.2.5.
-
(1) Let
 $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
 $\mu $
-display over
$\mu $
-display over
 $({\mathcal O}, (\pi ))=(\mathfrak {S}_{{\mathcal O}, 1}, (\mathcal {E}))$
. Let
$({\mathcal O}, (\pi ))=(\mathfrak {S}_{{\mathcal O}, 1}, (\mathcal {E}))$
. Let
 $m \geq 1$
be an integer. Any deformation of
$m \geq 1$
be an integer. Any deformation of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E}))$
has no nontrivial automorphisms. Moreover, any deformation of
$(\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E}))$
has no nontrivial automorphisms. Moreover, any deformation of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
has no nontrivial automorphisms.
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
has no nontrivial automorphisms. -
(2) Let
 $m \geq 1$
be an integer. For a G-
$m \geq 1$
be an integer. For a G-
 $\mu $
-display
$\mu $
-display
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ], I_S)$
, any deformation of
$(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ], I_S)$
, any deformation of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
has no nontrivial automorphisms.
$(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
has no nontrivial automorphisms.
Proof. (1) By Example 3.1.6, it suffices to prove the first assertion. This follows by applying Proposition 3.2.7 (2) to special nilpotent thickenings
![]() $(\mathfrak {S}_{{\mathcal O}, l+1}, (\mathcal {E})) \to (\mathfrak {S}_{{\mathcal O}, l}, (\mathcal {E}))$
$(\mathfrak {S}_{{\mathcal O}, l+1}, (\mathcal {E})) \to (\mathfrak {S}_{{\mathcal O}, l}, (\mathcal {E}))$
![]() $(1 \leq l \leq m-1)$
repeatedly.
$(1 \leq l \leq m-1)$
repeatedly.
(2) This also follows from Proposition 3.2.7 (2).
3.3 Period maps
Let
![]() $f \colon (A', I') \to (A, I)$
be a special nilpotent thickening of orientable and bounded
$f \colon (A', I') \to (A, I)$
be a special nilpotent thickening of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
. Recall the Hodge filtration
$(A, I)$
. Recall the Hodge filtration
![]() $P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
from Section 2.5.
$P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
from Section 2.5.
Definition 3.3.1. Let
![]() $\mathscr {Q}$
be a G-torsor over
$\mathscr {Q}$
be a G-torsor over
![]() $ \mathrm {Spec} A'/I'$
with an isomorphism
$ \mathrm {Spec} A'/I'$
with an isomorphism
of G-torsors over
![]() $ \mathrm {Spec} A/I$
. A lift of the Hodge filtration
$ \mathrm {Spec} A/I$
. A lift of the Hodge filtration
![]() $P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
in
$P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
in
![]() $\mathscr {Q}$
is a pair
$\mathscr {Q}$
is a pair
![]() $(\mathscr {P}, \iota )$
of a
$(\mathscr {P}, \iota )$
of a
![]() $P_\mu $
-torsor
$P_\mu $
-torsor
![]() $\mathscr {P}$
over
$\mathscr {P}$
over
![]() $ \mathrm {Spec} A'/I'$
and a
$ \mathrm {Spec} A'/I'$
and a
![]() $P_\mu $
-equivariant morphism
$P_\mu $
-equivariant morphism
![]() $\iota \colon \mathscr {P} \to \mathscr {Q}$
such that the isomorphism
$\iota \colon \mathscr {P} \to \mathscr {Q}$
such that the isomorphism
![]() $f^*\mathscr {Q} \overset {\sim }{\to } \mathcal {Q}_{A/I}$
restricts to an isomorphism
$f^*\mathscr {Q} \overset {\sim }{\to } \mathcal {Q}_{A/I}$
restricts to an isomorphism
![]() $f^*\mathscr {P} \overset {\sim }{\to } P(\mathcal {Q})_{A/I}$
.
$f^*\mathscr {P} \overset {\sim }{\to } P(\mathcal {Q})_{A/I}$
.
There is an obvious notion of isomorphism of lifts of the Hodge filtration. We note that there is at most one isomorphism between two lifts. Let
be the set of isomorphism classes of lifts of the Hodge filtration
![]() $P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
in
$P(\mathcal {Q})_{A/I} \to \mathcal {Q}_{A/I}$
in
![]() $\mathscr {Q}$
.
$\mathscr {Q}$
.
Example 3.3.2. For a deformation
![]() $\mathscr {Q}$
of
$\mathscr {Q}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
, the pair
$(A', I')$
, the pair
is a lift of the Hodge filtration
![]() $P(\mathcal {Q})_{A/I}$
in
$P(\mathcal {Q})_{A/I}$
in
![]() $\mathscr {Q}_{A'/I'}$
.
$\mathscr {Q}_{A'/I'}$
.
Definition 3.3.3 (Period map).
Let
![]() $\mathscr {Q}$
be a deformation of
$\mathscr {Q}$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
. We define a map of sets
$(A', I')$
. We define a map of sets
as follows. Let
![]() $\mathscr {R} \in {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
be a deformation of
$\mathscr {R} \in {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
. By Proposition 3.2.7, there exists a unique isomorphism
$(A', I')$
. By Proposition 3.2.7, there exists a unique isomorphism
![]() $ \psi \colon \mathscr {R}_{\phi } \overset {\sim }{\to } \mathscr {Q}_{\phi } $
of deformations of the underlying G-
$ \psi \colon \mathscr {R}_{\phi } \overset {\sim }{\to } \mathscr {Q}_{\phi } $
of deformations of the underlying G-
![]() $\phi $
-module
$\phi $
-module
![]() $\mathcal {Q}_{\phi }$
. In particular,
$\mathcal {Q}_{\phi }$
. In particular,
![]() $\psi $
induces an isomorphism
$\psi $
induces an isomorphism
![]() $\mathscr {R}_{A'/I'} \overset {\sim }{\to } \mathscr {Q}_{A'/I'}$
of G-torsors over
$\mathscr {R}_{A'/I'} \overset {\sim }{\to } \mathscr {Q}_{A'/I'}$
of G-torsors over
![]() $ \mathrm {Spec} A'/I'$
. We define the map
$ \mathrm {Spec} A'/I'$
. We define the map
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
by sending
$ {\mathrm {Per}} _{\mathscr {Q}}$
by sending
![]() $\mathscr {R}$
to the lift
$\mathscr {R}$
to the lift
We call
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
the period map associated with the deformation
$ {\mathrm {Per}} _{\mathscr {Q}}$
the period map associated with the deformation
![]() $\mathscr {Q}$
.
$\mathscr {Q}$
.
The main result of this section is the following theorem, which can be seen as an analogue of the Grothendieck–Messing deformation theory.
Theorem 3.3.4. Let
![]() $f \colon (A', I') \to (A, I)$
be a special nilpotent thickening of orientable and bounded
$f \colon (A', I') \to (A, I)$
be a special nilpotent thickening of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
, and we fix a deformation
$(A, I)$
, and we fix a deformation
![]() $\mathscr {Q}$
of
$\mathscr {Q}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
. If the cocharacter
$(A', I')$
. If the cocharacter
![]() $\mu $
is 1-bounded, then the period map
$\mu $
is 1-bounded, then the period map
is bijective.
Proof. By Corollary 3.2.9, we may work
![]() $(\pi , I')$
-completely étale locally on
$(\pi , I')$
-completely étale locally on
![]() $A'$
. We may thus assume that
$A'$
. We may thus assume that
![]() $\mathcal {Q}=\mathcal {Q}_X$
for some
$\mathcal {Q}=\mathcal {Q}_X$
for some
![]() $X \in G(A)_I$
. We shall prove that
$X \in G(A)_I$
. We shall prove that
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
is injective. Let
$ {\mathrm {Per}} _{\mathscr {Q}}$
is injective. Let
![]() $\mathscr {R}$
and
$\mathscr {R}$
and
![]() $\mathscr {S}$
be two deformations of
$\mathscr {S}$
be two deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
such that
$(A', I')$
such that
![]() $P(\mathscr {R})_{A'/I'} = P(\mathscr {S})_{A'/I'}$
in
$P(\mathscr {R})_{A'/I'} = P(\mathscr {S})_{A'/I'}$
in
![]() $ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
. By Proposition 3.1.4, we may further assume that
$ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
. By Proposition 3.1.4, we may further assume that
for some
![]() $X', Y, Z \in \mathbf {Def}(X)_{(A', I')}$
. Then
$X', Y, Z \in \mathbf {Def}(X)_{(A', I')}$
. Then
![]() $\mathscr {Q}_{A'/I'}$
is naturally identified with
$\mathscr {Q}_{A'/I'}$
is naturally identified with
![]() $G_{A'/I'}$
, and the isomorphism
$G_{A'/I'}$
, and the isomorphism
![]() $f^*(\mathscr {Q}_{A'/I'}) \overset {\sim }{\to } \mathcal {Q}_{A/I}$
agrees with the canonical isomorphism
$f^*(\mathscr {Q}_{A'/I'}) \overset {\sim }{\to } \mathcal {Q}_{A/I}$
agrees with the canonical isomorphism
![]() $f^*G_{A'/I'} \overset {\sim }{\to } G_{A/I}$
. We fix a generator
$f^*G_{A'/I'} \overset {\sim }{\to } G_{A/I}$
. We fix a generator
![]() $d \in I'$
. The period map
$d \in I'$
. The period map
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
sends
$ {\mathrm {Per}} _{\mathscr {Q}}$
sends
![]() $(\mathcal {Q}_Y, 1)$
and
$(\mathcal {Q}_Y, 1)$
and
![]() $(\mathcal {Q}_Z, 1)$
to
$(\mathcal {Q}_Z, 1)$
to
respectively, where
![]() $\iota _{X^{\prime }_d(Y_d)^{-1}} \colon (P_{\mu })_{A'/I'} \hookrightarrow G_{A'/I'}$
is defined by
$\iota _{X^{\prime }_d(Y_d)^{-1}} \colon (P_{\mu })_{A'/I'} \hookrightarrow G_{A'/I'}$
is defined by
![]() $g \mapsto X^{\prime }_d(Y_d)^{-1}g$
, and similarly for
$g \mapsto X^{\prime }_d(Y_d)^{-1}g$
, and similarly for
![]() $\iota _{X^{\prime }_d(Z_d)^{-1}}$
. (See (2.1) for the notation
$\iota _{X^{\prime }_d(Z_d)^{-1}}$
. (See (2.1) for the notation
![]() $X_d$
.) Since the two lifts are isomorphic, the image of
$X_d$
.) Since the two lifts are isomorphic, the image of
![]() $Z_d(Y_d)^{-1}$
in
$Z_d(Y_d)^{-1}$
in
![]() $G(A'/I')$
belongs to
$G(A'/I')$
belongs to
![]() $P_\mu (A'/I')$
. This implies that
$P_\mu (A'/I')$
. This implies that
![]() $Z_d(Y_d)^{-1} \in G_\mu (A', I')$
by Proposition 2.3.3 since
$Z_d(Y_d)^{-1} \in G_\mu (A', I')$
by Proposition 2.3.3 since
![]() $\mu $
is 1-bounded. Then
$\mu $
is 1-bounded. Then
![]() $Z_d(Y_d)^{-1}$
gives
$Z_d(Y_d)^{-1}$
gives
![]() $(\mathcal {Q}_Y, 1) \overset {\sim }{\to } (\mathcal {Q}_Z, 1)$
by Remark 3.2.8.
$(\mathcal {Q}_Y, 1) \overset {\sim }{\to } (\mathcal {Q}_Z, 1)$
by Remark 3.2.8.
We next prove that
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
is surjective. We may assume that
$ {\mathrm {Per}} _{\mathscr {Q}}$
is surjective. We may assume that
![]() $\mathscr {Q}=(\mathcal {Q}_{X'}, 1)$
as above. Let
$\mathscr {Q}=(\mathcal {Q}_{X'}, 1)$
as above. Let
![]() $(\mathscr {P}, \iota ) \in {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
. By the same argument as in the proof of Lemma 3.1.2, we see that
$(\mathscr {P}, \iota ) \in {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
. By the same argument as in the proof of Lemma 3.1.2, we see that
![]() $\mathscr {P}$
is trivial as a
$\mathscr {P}$
is trivial as a
![]() $P_\mu $
-torsor. Then, with the notation as above, this lift can be identified with
$P_\mu $
-torsor. Then, with the notation as above, this lift can be identified with
![]() $ ((P_{\mu })_{A'/I'}, \iota _{x}) $
for some
$ ((P_{\mu })_{A'/I'}, \iota _{x}) $
for some
![]() $x \in G(A'/I')$
whose image in
$x \in G(A'/I')$
whose image in
![]() $G(A/I)$
is
$G(A/I)$
is
![]() $1$
. By Lemma 3.3.5 below, after replacing x by
$1$
. By Lemma 3.3.5 below, after replacing x by
![]() $x t$
for some
$x t$
for some
![]() $t \in P_\mu (A'/I')$
, we can find an element
$t \in P_\mu (A'/I')$
, we can find an element
![]() $\widetilde {x} \in G(A')$
such that
$\widetilde {x} \in G(A')$
such that
![]() $f(\widetilde {x})=1$
in
$f(\widetilde {x})=1$
in
![]() $G(A)$
and the image of
$G(A)$
and the image of
![]() $\widetilde {x}$
in
$\widetilde {x}$
in
![]() $G(A'/I')$
coincides with x. We then define
$G(A'/I')$
coincides with x. We then define
![]() $Y \in \mathbf {Def}(X)_{(A', I')}$
to be the unique object such that
$Y \in \mathbf {Def}(X)_{(A', I')}$
to be the unique object such that
![]() $Y_d=\widetilde {x}^{-1} X^{\prime }_d$
. By construction, the period map
$Y_d=\widetilde {x}^{-1} X^{\prime }_d$
. By construction, the period map
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
sends
$ {\mathrm {Per}} _{\mathscr {Q}}$
sends
![]() $(\mathcal {Q}_Y, 1)$
to
$(\mathcal {Q}_Y, 1)$
to
![]() $((P_{\mu })_{A'/I'}, \iota _{x})$
. This concludes the proof of the surjectivity of
$((P_{\mu })_{A'/I'}, \iota _{x})$
. This concludes the proof of the surjectivity of
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
, and hence that of Theorem 3.3.4.
$ {\mathrm {Per}} _{\mathscr {Q}}$
, and hence that of Theorem 3.3.4.
The following lemma is used in the proof of Theorem 3.3.4.
Lemma 3.3.5. Let the notation be as in Theorem 3.3.4. Let
![]() $x \in G(A'/I')$
be such that
$x \in G(A'/I')$
be such that
![]() $f(x)=1$
in
$f(x)=1$
in
![]() $G(A/I)$
. Then there exist
$G(A/I)$
. Then there exist
![]() $t \in P_\mu (A'/I')$
and
$t \in P_\mu (A'/I')$
and
![]() $\widetilde {x} \in G(A')$
such that
$\widetilde {x} \in G(A')$
such that
![]() $f(\widetilde {x})=1$
in
$f(\widetilde {x})=1$
in
![]() $G(A)$
and the image of
$G(A)$
and the image of
![]() $\widetilde {x}$
in
$\widetilde {x}$
in
![]() $G(A'/I')$
is equal to
$G(A'/I')$
is equal to
![]() $x t$
.
$x t$
.
Proof. Since G is smooth and
![]() $A'$
is
$A'$
is
![]() $I'$
-adically complete, the map
$I'$
-adically complete, the map
![]() $G(A') \to G(A'/I')$
is surjective. Let
$G(A') \to G(A'/I')$
is surjective. Let
![]() $\widetilde {x}_1 \in G(A')$
be an element which is mapped to
$\widetilde {x}_1 \in G(A')$
be an element which is mapped to
![]() $x \in G(A'/I')$
. By Proposition 2.3.3, we have
$x \in G(A'/I')$
. By Proposition 2.3.3, we have
![]() $f(\widetilde {x}_1) \in G_\mu (A, I)$
. By Lemma 3.1.3, there is an element
$f(\widetilde {x}_1) \in G_\mu (A, I)$
. By Lemma 3.1.3, there is an element
![]() $\widetilde {x}_2 \in G_\mu (A', I')$
such that
$\widetilde {x}_2 \in G_\mu (A', I')$
such that
![]() $f(\widetilde {x}_2)=f(\widetilde {x}_1)$
in
$f(\widetilde {x}_2)=f(\widetilde {x}_1)$
in
![]() $G_\mu (A, I)$
. The image
$G_\mu (A, I)$
. The image
![]() $t \in G(A'/I')$
of
$t \in G(A'/I')$
of
![]() $\widetilde {x}^{-1}_2$
belongs to
$\widetilde {x}^{-1}_2$
belongs to
![]() $P_\mu (A'/I')$
. Then t and
$P_\mu (A'/I')$
. Then t and
![]() $\widetilde {x}:=\widetilde {x}_1\widetilde {x}^{-1}_2$
have the desired properties.
$\widetilde {x}:=\widetilde {x}_1\widetilde {x}^{-1}_2$
have the desired properties.
Remark 3.3.6. A banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
admits a deformation over
$(A, I)$
admits a deformation over
![]() $(A', I')$
since
$(A', I')$
since
![]() $G(A') \to G(A)$
is surjective. However, for a G-
$G(A') \to G(A)$
is surjective. However, for a G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A, I)$
which is not necessarily banal, the existence of a deformation of
$(A, I)$
which is not necessarily banal, the existence of a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
is not clear. In Proposition 3.4.6 below, under a mild additional assumption on
$(A', I')$
is not clear. In Proposition 3.4.6 below, under a mild additional assumption on
![]() $f \colon (A', I') \to (A, I)$
, we will prove that a deformation of
$f \colon (A', I') \to (A, I)$
, we will prove that a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
exists if
$(A', I')$
exists if
![]() $\mu $
is 1-bounded.
$\mu $
is 1-bounded.
3.4 Normalized period maps
Let
![]() $f \colon (A', I') \to (A, I)$
be a special nilpotent thickening of orientable and bounded
$f \colon (A', I') \to (A, I)$
be a special nilpotent thickening of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
. In this subsection, we assume that f satisfies the following assumption:
${\mathcal O}$
. In this subsection, we assume that f satisfies the following assumption:
Assumption 3.4.1. The kernel K of
![]() $A'/I' \to A/I$
satisfies
$A'/I' \to A/I$
satisfies
![]() $K^2=0$
. Moreover, there exists an integer
$K^2=0$
. Moreover, there exists an integer
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $\pi ^n=0$
in
$\pi ^n=0$
in
![]() $A'/I'$
.
$A'/I'$
.
Remark 3.4.2. A special nilpotent thickening of Breuil–Kisin type or of perfectoid type (Example 3.2.6) satisfies Assumption 3.4.1.
Let
![]() $\mathcal {Q}$
be a banal G-
$\mathcal {Q}$
be a banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
. The quotient (fppf) sheaf
$(A, I)$
. The quotient (fppf) sheaf
is representable by a scheme over
![]() $ \mathrm {Spec} A/I$
, which is also denoted by
$ \mathrm {Spec} A/I$
, which is also denoted by
![]() $X_\mu (\mathcal {Q})$
. (To see this, it suffices to show that the quotient sheaf
$X_\mu (\mathcal {Q})$
. (To see this, it suffices to show that the quotient sheaf
![]() $G_{{\mathcal O}/\pi ^n}/(P_\mu )_{{\mathcal O}/\pi ^n}$
is representable, which follows from [Reference Demazure and GrothendieckDG70, Expose
$G_{{\mathcal O}/\pi ^n}/(P_\mu )_{{\mathcal O}/\pi ^n}$
is representable, which follows from [Reference Demazure and GrothendieckDG70, Expose
![]() $V$
, Théorème 3.2]. We note that
$V$
, Théorème 3.2]. We note that
![]() $\mathcal {Q}_{A/I} \simeq G_{A/I}$
since
$\mathcal {Q}_{A/I} \simeq G_{A/I}$
since
![]() $\mathcal {Q}$
is banal.) The closed immersion
$\mathcal {Q}$
is banal.) The closed immersion
![]() $P(\mathcal {Q})_{A/I} \hookrightarrow \mathcal {Q}_{A/I}$
induces a section
$P(\mathcal {Q})_{A/I} \hookrightarrow \mathcal {Q}_{A/I}$
induces a section
The
![]() $A/I$
-module corresponding to the conormal sheaf of
$A/I$
-module corresponding to the conormal sheaf of
![]() $s_{\mathcal {Q}}$
on
$s_{\mathcal {Q}}$
on
![]() $ \mathrm {Spec} A/I$
is denoted by
$ \mathrm {Spec} A/I$
is denoted by
![]() $C(\mathcal {Q})$
. We call
$C(\mathcal {Q})$
. We call
![]() $C(\mathcal {Q})$
the conormal module.
$C(\mathcal {Q})$
the conormal module.
Definition 3.4.3. Let
![]() ${\mathcal O}_{U^{-}_{\mu }, 1}$
be the local ring of
${\mathcal O}_{U^{-}_{\mu }, 1}$
be the local ring of
![]() $U^{-}_{\mu }$
at
$U^{-}_{\mu }$
at
![]() $1 \in U^{-}_{\mu }(k)$
and let
$1 \in U^{-}_{\mu }(k)$
and let
be the completion of
![]() ${\mathcal O}_{U^{-}_{\mu }, 1}$
with respect to the maximal ideal. We denote by
${\mathcal O}_{U^{-}_{\mu }, 1}$
with respect to the maximal ideal. We denote by
![]() $ J_{G, \mu } \subset R_{G, \mu } $
the kernel of the homomorphism
$ J_{G, \mu } \subset R_{G, \mu } $
the kernel of the homomorphism
![]() $\epsilon \colon R_{G, \mu } \to {\mathcal O}$
induced by the unit morphism
$\epsilon \colon R_{G, \mu } \to {\mathcal O}$
induced by the unit morphism
![]() $ \mathrm {Spec} {\mathcal O} \to U^{-}_{\mu }$
. We set
$ \mathrm {Spec} {\mathcal O} \to U^{-}_{\mu }$
. We set
which is a free
![]() ${\mathcal O}$
-module of finite rank.
${\mathcal O}$
-module of finite rank.
Example 3.4.4. An isomorphism
![]() $\mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X}$
of G-
$\mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X}$
of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
for an element
$(A, I)$
for an element
![]() $X \in G(A)_I$
induces
$X \in G(A)_I$
induces
![]() $ X_\mu (\mathcal {Q}) \overset {\sim }{\to } G_{A/I}/(P_\mu )_{A/I} $
and
$ X_\mu (\mathcal {Q}) \overset {\sim }{\to } G_{A/I}/(P_\mu )_{A/I} $
and
![]() $ C(R_{G, \mu }) \otimes _{\mathcal O} A/I \overset {\sim }{\to } C(\mathcal {Q}). $
$ C(R_{G, \mu }) \otimes _{\mathcal O} A/I \overset {\sim }{\to } C(\mathcal {Q}). $
In the following, for modules M and N over a ring R, the set of R-linear homomorphisms
![]() $M \to N$
is denoted by
$M \to N$
is denoted by
![]() $ {\mathrm {Hom}} _R(M, N)$
.
$ {\mathrm {Hom}} _R(M, N)$
.
Lemma 3.4.5. Let
![]() $\mathcal {Q}$
be a banal G-
$\mathcal {Q}$
be a banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
, and let
$(A, I)$
, and let
![]() $\mathscr {Q}$
be a deformation of
$\mathscr {Q}$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
. Then there exists a natural bijection
$(A', I')$
. Then there exists a natural bijection
(Since
![]() $K^2=0$
, the ideal
$K^2=0$
, the ideal
![]() $K \subset A'/I'$
can be naturally regarded as an
$K \subset A'/I'$
can be naturally regarded as an
![]() $A/I$
-module.)
$A/I$
-module.)
Proof. As above, the Hodge filtration
![]() $P(\mathscr {Q})_{A'/I'} \to \mathscr {Q}_{A'/I'}$
induces a section
$P(\mathscr {Q})_{A'/I'} \to \mathscr {Q}_{A'/I'}$
induces a section
Let
![]() $C(\mathscr {Q})$
be the conormal module of
$C(\mathscr {Q})$
be the conormal module of
![]() $s_{\mathscr {Q}}$
. We have
$s_{\mathscr {Q}}$
. We have
![]() $C(\mathscr {Q})\otimes _{A'/I'} A/I \simeq C(\mathcal {Q})$
. Let
$C(\mathscr {Q})\otimes _{A'/I'} A/I \simeq C(\mathcal {Q})$
. Let
![]() $s \colon \mathrm {Spec} A/I \hookrightarrow X_\mu (\mathscr {Q})$
be the composition of
$s \colon \mathrm {Spec} A/I \hookrightarrow X_\mu (\mathscr {Q})$
be the composition of
![]() $s_{\mathscr {Q}}$
with
$s_{\mathscr {Q}}$
with
![]() $ \mathrm {Spec} A/I \hookrightarrow \mathrm {Spec} A'/I'$
, and let
$ \mathrm {Spec} A/I \hookrightarrow \mathrm {Spec} A'/I'$
, and let
![]() $C_s$
be the conormal module of s. We have a natural homomorphism
$C_s$
be the conormal module of s. We have a natural homomorphism
![]() $ C(\mathscr {Q})\otimes _{A'/I'} A/I \to C_s $
of
$ C(\mathscr {Q})\otimes _{A'/I'} A/I \to C_s $
of
![]() $A/I$
-modules.
$A/I$
-modules.
Let
![]() $\iota \colon \mathscr {P} \to \mathscr {Q}_{A'/I'}$
be a lift of
$\iota \colon \mathscr {P} \to \mathscr {Q}_{A'/I'}$
be a lift of
![]() $P(\mathcal {Q})_{A/I}$
. In the same way as above, this induces a section
$P(\mathcal {Q})_{A/I}$
. In the same way as above, this induces a section
![]() $ s_{\mathscr {P}} \colon \mathrm {Spec} A'/I' \to X_\mu (\mathscr {Q}). $
Since the composition of
$ s_{\mathscr {P}} \colon \mathrm {Spec} A'/I' \to X_\mu (\mathscr {Q}). $
Since the composition of
![]() $s_{\mathscr {P}}$
with
$s_{\mathscr {P}}$
with
![]() $ \mathrm {Spec} A/I \hookrightarrow \mathrm {Spec} A'/I'$
is equal to s, the morphism
$ \mathrm {Spec} A/I \hookrightarrow \mathrm {Spec} A'/I'$
is equal to s, the morphism
![]() $s_{\mathscr {P}}$
induces a homomorphism
$s_{\mathscr {P}}$
induces a homomorphism
![]() $t_{\mathscr {P}} \colon C_s \to K$
of
$t_{\mathscr {P}} \colon C_s \to K$
of
![]() $A/I$
-modules (defined by
$A/I$
-modules (defined by
![]() $x \mapsto s^*_{\mathscr {P}}(x)$
). Associating to
$x \mapsto s^*_{\mathscr {P}}(x)$
). Associating to
![]() $\iota \colon \mathscr {P} \to \mathscr {Q}_{A'/I'}$
the composition
$\iota \colon \mathscr {P} \to \mathscr {Q}_{A'/I'}$
the composition
we obtain a map
We shall prove that this map is bijective. For this, we may assume that
![]() $\mathcal {Q}=\mathcal {Q}_X$
for some
$\mathcal {Q}=\mathcal {Q}_X$
for some
![]() $X \in G(A)_I$
and
$X \in G(A)_I$
and
![]() $\mathscr {Q}=(\mathcal {Q}_{X'}, 1)$
for some
$\mathscr {Q}=(\mathcal {Q}_{X'}, 1)$
for some
![]() $X' \in \mathbf {Def}(X)_{(A', I')}$
as in the proof of Theorem 3.3.4. Then we have
$X' \in \mathbf {Def}(X)_{(A', I')}$
as in the proof of Theorem 3.3.4. Then we have
![]() $P(\mathcal {Q})_{A/I}=(P_\mu )_{A/I}$
and
$P(\mathcal {Q})_{A/I}=(P_\mu )_{A/I}$
and
![]() $\mathscr {Q}_{A'/I'}=G_{A'/I'}$
, and by the argument in the proof of Theorem 3.3.4, we can identify
$\mathscr {Q}_{A'/I'}=G_{A'/I'}$
, and by the argument in the proof of Theorem 3.3.4, we can identify
![]() $ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
with the set of
$ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
with the set of
![]() $P_\mu (A'/I')$
-orbits
$P_\mu (A'/I')$
-orbits
![]() $ x P_\mu (A'/I') \subset G(A'/I') $
of elements x of the kernel of
$ x P_\mu (A'/I') \subset G(A'/I') $
of elements x of the kernel of
![]() $G(A'/I') \to G(A/I)$
. We note that for such elements x, there are elements
$G(A'/I') \to G(A/I)$
. We note that for such elements x, there are elements
![]() $u \in U^-_{\mu }(A'/I')$
and
$u \in U^-_{\mu }(A'/I')$
and
![]() $t \in P_\mu (A'/I')$
such that
$t \in P_\mu (A'/I')$
such that
![]() $x=ut$
since the multiplication map
$x=ut$
since the multiplication map
is an open immersion; see also the proof of [Reference ItoIto23, Proposition 4.2.8]. Thus, we can identify
![]() $ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
with the set of
$ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
with the set of
![]() $P_\mu (A'/I')$
-orbits
$P_\mu (A'/I')$
-orbits
![]() $ x P_\mu (A'/I') \subset G(A'/I') $
of elements x of the kernel of
$ x P_\mu (A'/I') \subset G(A'/I') $
of elements x of the kernel of
![]() $U^{-}_{\mu }(A'/I') \to U^{-}_{\mu }(A/I)$
. Using this observation and using the fact that
$U^{-}_{\mu }(A'/I') \to U^{-}_{\mu }(A/I)$
. Using this observation and using the fact that
![]() $U^{-}_{\mu } \times _{ \mathrm {Spec} {\mathcal O}} P_\mu \to G_{\mathcal O}$
is an open immersion again, we can identify
$U^{-}_{\mu } \times _{ \mathrm {Spec} {\mathcal O}} P_\mu \to G_{\mathcal O}$
is an open immersion again, we can identify
![]() $ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
with the kernel of
$ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'})$
with the kernel of
![]() $U^{-}_{\mu }(A'/I') \to U^{-}_{\mu }(A/I)$
. However, by Example 3.4.4, we have
$U^{-}_{\mu }(A'/I') \to U^{-}_{\mu }(A/I)$
. However, by Example 3.4.4, we have
The map
![]() $ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'}) \to {\mathrm {Hom}} _{A/I}(C(\mathcal {Q}), K) $
sends an element
$ {\mathrm {Lift}} (P(\mathcal {Q})_{A/I}, \mathscr {Q}_{A'/I'}) \to {\mathrm {Hom}} _{A/I}(C(\mathcal {Q}), K) $
sends an element
![]() $x \colon \mathrm {Spec} A'/I' \to U^{-}_{\mu }$
of the kernel of
$x \colon \mathrm {Spec} A'/I' \to U^{-}_{\mu }$
of the kernel of
![]() $U^{-}_{\mu }(A'/I') \to U^{-}_{\mu }(A/I)$
to the map
$U^{-}_{\mu }(A'/I') \to U^{-}_{\mu }(A/I)$
to the map
![]() $x^* \colon C(R_{G, \mu }) \to K$
. Using this description, it is easy to see that this map is bijective.
$x^* \colon C(R_{G, \mu }) \to K$
. Using this description, it is easy to see that this map is bijective.
The proof of the following result is inspired by that of [Reference Bültel and PappasBP20, Theorem 3.5.11].
Proposition 3.4.6. Assume that
![]() $\mu $
is 1-bounded. Let
$\mu $
is 1-bounded. Let
![]() $\mathcal {Q}$
be a (not necessarily banal) G-
$\mathcal {Q}$
be a (not necessarily banal) G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
. If
$(A, I)$
. If
![]() $f \colon (A', I') \to (A, I)$
satisfies Assumption 3.4.1, then the set
$f \colon (A', I') \to (A, I)$
satisfies Assumption 3.4.1, then the set
![]() $ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
of isomorphism classes of deformations of
$ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
of isomorphism classes of deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
has the structure of a torsor under an
$(A', I')$
has the structure of a torsor under an
![]() $A/I$
-module. In particular,
$A/I$
-module. In particular,
![]() $ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
is nonempty.
$ {\mathrm {Def}} (\mathcal {Q})_{(A', I')}$
is nonempty.
Proof. We recall that the functor
![]() $ (A', I')_{\mathrm {\acute {e}t}} \to (A, I)_{\mathrm {\acute {e}t}} $
defined by
$ (A', I')_{\mathrm {\acute {e}t}} \to (A, I)_{\mathrm {\acute {e}t}} $
defined by
![]() $ B' \mapsto B, $
where B is the
$ B' \mapsto B, $
where B is the
![]() $(\pi , I)$
-adic completion of
$(\pi , I)$
-adic completion of
![]() $B' \otimes _{A'} A$
, is an equivalence. Moreover, any
$B' \otimes _{A'} A$
, is an equivalence. Moreover, any
![]() $\pi $
-completely étale homomorphism
$\pi $
-completely étale homomorphism
![]() $A/I \to C$
is étale since
$A/I \to C$
is étale since
![]() $\pi ^n=0$
in
$\pi ^n=0$
in
![]() $A/I$
, and thus, the category
$A/I$
, and thus, the category
![]() $(A, I)_{\mathrm {\acute {e}t}}$
is equivalent to the category
$(A, I)_{\mathrm {\acute {e}t}}$
is equivalent to the category
![]() $(A/I)_{\mathrm {\acute {e}t}}$
of étale
$(A/I)_{\mathrm {\acute {e}t}}$
of étale
![]() $A/I$
-algebras (see [Reference ItoIto23, Lemma 2.5.9]).
$A/I$
-algebras (see [Reference ItoIto23, Lemma 2.5.9]).
By Corollary 3.2.9, the functor
forms a sheaf. Let
![]() $B' \in (A', I')_{\mathrm {\acute {e}t}}$
be such that
$B' \in (A', I')_{\mathrm {\acute {e}t}}$
be such that
![]() $\mathcal {Q}_{(B, IB)}$
is banal. We choose a deformation
$\mathcal {Q}_{(B, IB)}$
is banal. We choose a deformation
![]() $\mathscr {Q}$
of
$\mathscr {Q}$
of
![]() $\mathcal {Q}_{(B, IB)}$
over
$\mathcal {Q}_{(B, IB)}$
over
![]() $(B', I'B')$
, which exists since
$(B', I'B')$
, which exists since
![]() $G(B') \to G(B)$
is surjective. To simplify the notation, the base change
$G(B') \to G(B)$
is surjective. To simplify the notation, the base change
![]() $\mathcal {Q}_{(B, IB)}$
is also denoted by
$\mathcal {Q}_{(B, IB)}$
is also denoted by
![]() $\mathcal {Q}$
. By Theorem 3.3.4, the period map
$\mathcal {Q}$
. By Theorem 3.3.4, the period map
is bijective. By Lemma 3.4.5, we have
We note that
![]() $K \otimes _{A/I} B/IB$
is the kernel of
$K \otimes _{A/I} B/IB$
is the kernel of
![]() $B'/I'B' \to B/IB$
. We endow the set
$B'/I'B' \to B/IB$
. We endow the set
![]() $\underline { {\mathrm {Def}} }(\mathcal {Q})(B')$
with an action of the
$\underline { {\mathrm {Def}} }(\mathcal {Q})(B')$
with an action of the
![]() $B/IB$
-module
$B/IB$
-module
![]() $ {\mathrm {Hom}} _{B/IB}(C(\mathcal {Q}), K \otimes _{A/I} B/IB)$
via these identifications. One can check that this action does not depend on the choice of
$ {\mathrm {Hom}} _{B/IB}(C(\mathcal {Q}), K \otimes _{A/I} B/IB)$
via these identifications. One can check that this action does not depend on the choice of
![]() $\mathscr {Q}$
. By étale descent for quasi-coherent sheaves, the
$\mathscr {Q}$
. By étale descent for quasi-coherent sheaves, the
![]() $B/IB$
-modules
$B/IB$
-modules
![]() $ {\mathrm {Hom}} _{B/IB}(C(\mathcal {Q}), K \otimes _{A/I} B/IB)$
give rise to a quasi-coherent sheaf
$ {\mathrm {Hom}} _{B/IB}(C(\mathcal {Q}), K \otimes _{A/I} B/IB)$
give rise to a quasi-coherent sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $(A/I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
, and
$(A/I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
, and
![]() $\underline { {\mathrm {Def}} }(\mathcal {Q})$
is an
$\underline { {\mathrm {Def}} }(\mathcal {Q})$
is an
![]() $\mathcal {F}$
-torsor on
$\mathcal {F}$
-torsor on
![]() $(A/I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
. Since any
$(A/I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
. Since any
![]() $\mathcal {F}$
-torsor on
$\mathcal {F}$
-torsor on
![]() $(A/I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
is trivial, the result follows.
$(A/I)^{ {\mathrm {op}} }_{\mathrm {\acute {e}t}}$
is trivial, the result follows.
In the following, the maximal ideal of a local ring R is denoted by
![]() $\mathfrak {m}_R$
.
$\mathfrak {m}_R$
.
Remark 3.4.7. For a local ring R with a local homomorphism
![]() ${\mathcal O} \to R$
, we define
${\mathcal O} \to R$
, we define
which is called the tangent space of R over
![]() ${\mathcal O}$
. When
${\mathcal O}$
. When
![]() $R=R_{G, \mu }$
, we write
$R=R_{G, \mu }$
, we write
![]() $ \mathfrak {m}_{G, \mu }:=\mathfrak {m}_{R_{G, \mu }} $
and
$ \mathfrak {m}_{G, \mu }:=\mathfrak {m}_{R_{G, \mu }} $
and
![]() $ \mathfrak {t}_{G, \mu }:=\mathfrak {t}_{R_{G, \mu }} $
for simplicity. The natural homomorphism
$ \mathfrak {t}_{G, \mu }:=\mathfrak {t}_{R_{G, \mu }} $
for simplicity. The natural homomorphism
is an isomorphism.
Remark 3.4.8 (Normalized period map).
We assume that K is killed by
![]() $\pi $
, so that K is a k-vector space. Let
$\pi $
, so that K is a k-vector space. Let
![]() $\mathcal {Q}$
be a banal G-
$\mathcal {Q}$
be a banal G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $(A, I)$
and
$(A, I)$
and
![]() $\mathscr {Q}$
a deformation of
$\mathscr {Q}$
a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(A', I')$
. We choose an isomorphism
$(A', I')$
. We choose an isomorphism
![]() $\beta \colon \mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X}$
of G-
$\beta \colon \mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X}$
of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $(A, I)$
for some
$(A, I)$
for some
![]() $X \in G(A)_{I}$
. The isomorphism
$X \in G(A)_{I}$
. The isomorphism
![]() $\beta $
induces
$\beta $
induces
See Example 3.4.4 and Remark 3.4.7. By Lemma 3.4.5, we then obtain the following isomorphism:
We define
as the composition of
![]() $ {\mathrm {Per}} _{\mathscr {Q}}$
with the above isomorphism. We call
$ {\mathrm {Per}} _{\mathscr {Q}}$
with the above isomorphism. We call
![]() $ {\mathrm {Per}} ^{\beta }_{\mathscr {Q}}$
the normalized period map with respect to the isomorphism
$ {\mathrm {Per}} ^{\beta }_{\mathscr {Q}}$
the normalized period map with respect to the isomorphism
![]() $ \beta \colon \mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X}. $
$ \beta \colon \mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X}. $
If
![]() $\beta ' \colon \mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X'}$
is another isomorphism, then there exists an
$\beta ' \colon \mathcal {Q} \overset {\sim }{\to } \mathcal {Q}_{X'}$
is another isomorphism, then there exists an
![]() $A/I$
-linear isomorphism
$A/I$
-linear isomorphism
![]() $h \colon \mathfrak {t}_{G, \mu } \otimes _k K \overset {\sim }{\to } \mathfrak {t}_{G, \mu } \otimes _k K$
such that
$h \colon \mathfrak {t}_{G, \mu } \otimes _k K \overset {\sim }{\to } \mathfrak {t}_{G, \mu } \otimes _k K$
such that
![]() $ {\mathrm {Per}} ^{\beta '}_{\mathscr {Q}}=h \circ {\mathrm {Per}} ^{\beta }_{\mathscr {Q}}$
.
$ {\mathrm {Per}} ^{\beta '}_{\mathscr {Q}}=h \circ {\mathrm {Per}} ^{\beta }_{\mathscr {Q}}$
.
4 Universal deformations
This section is the main part of this paper. Throughout this section, we will assume that
![]() $\mu $
is 1-bounded. For a G-
$\mu $
is 1-bounded. For a G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $({\mathcal O}, (\pi ))$
, we construct a universal deformation of
$({\mathcal O}, (\pi ))$
, we construct a universal deformation of
![]() $\mathcal {Q}$
as a prismatic G-
$\mathcal {Q}$
as a prismatic G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $R_{G, \mu }$
, where
$R_{G, \mu }$
, where
![]() $R_{G, \mu }$
is the local ring defined in Definition 3.4.3. The precise definition of a universal deformation is explained below. We also give some characterizations of universal deformations.
$R_{G, \mu }$
is the local ring defined in Definition 3.4.3. The precise definition of a universal deformation is explained below. We also give some characterizations of universal deformations.
4.1 Definitions and main results
Recall that
![]() $\mathcal {C}_{\mathcal O}$
is the category of complete regular local rings R over
$\mathcal {C}_{\mathcal O}$
is the category of complete regular local rings R over
![]() ${\mathcal O}$
with residue field k. Let
${\mathcal O}$
with residue field k. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. The
$R \in \mathcal {C}_{\mathcal O}$
. The
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $ ({\mathcal O}, (\pi )) $
with the projection
$ ({\mathcal O}, (\pi )) $
with the projection
![]() $e \colon R \to k$
is an object of the category
$e \colon R \to k$
is an object of the category ![]() defined in Section 2.2.
defined in Section 2.2.
Definition 4.1.1. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. Let
$({\mathcal O}, (\pi ))$
. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. A deformation of
$R \in \mathcal {C}_{\mathcal O}$
. A deformation of
![]() $\mathcal {Q}$
over R is a pair
$\mathcal {Q}$
over R is a pair
![]() $(\mathfrak {Q}, \gamma )$
of a prismatic G-
$(\mathfrak {Q}, \gamma )$
of a prismatic G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}$
over R (Definition 2.6.1) and an isomorphism
$\mathfrak {Q}$
over R (Definition 2.6.1) and an isomorphism
![]() $ \gamma \colon \mathfrak {Q}_{({\mathcal O}, (\pi ))} \overset {\sim }{\to } \mathcal {Q} $
of G-
$ \gamma \colon \mathfrak {Q}_{({\mathcal O}, (\pi ))} \overset {\sim }{\to } \mathcal {Q} $
of G-
![]() $\mu $
-displays over
$\mu $
-displays over
![]() $({\mathcal O}, (\pi ))$
. An isomorphism
$({\mathcal O}, (\pi ))$
. An isomorphism
![]() $(\mathfrak {Q}, \gamma ) \overset {\sim }{\to } (\mathfrak {Q}', \gamma ')$
of deformations is an isomorphism
$(\mathfrak {Q}, \gamma ) \overset {\sim }{\to } (\mathfrak {Q}', \gamma ')$
of deformations is an isomorphism
![]() $\mathfrak {Q} \overset {\sim }{\to } \mathfrak {Q}'$
of prismatic G-
$\mathfrak {Q} \overset {\sim }{\to } \mathfrak {Q}'$
of prismatic G-
![]() $\mu $
-displays over R such that the induced isomorphism
$\mu $
-displays over R such that the induced isomorphism
![]() $\mathfrak {Q}_{({\mathcal O}, (\pi ))} \overset {\sim }{\to } \mathfrak {Q}^{\prime }_{({\mathcal O}, (\pi ))}$
makes the following diagram commute:
$\mathfrak {Q}_{({\mathcal O}, (\pi ))} \overset {\sim }{\to } \mathfrak {Q}^{\prime }_{({\mathcal O}, (\pi ))}$
makes the following diagram commute:

When there is no danger of confusion, we write
![]() $\mathfrak {Q}$
instead of
$\mathfrak {Q}$
instead of
![]() $(\mathfrak {Q}, \gamma )$
.
$(\mathfrak {Q}, \gamma )$
.
Remark 4.1.2. Let
![]() $(\mathfrak {Q}, \gamma )$
be a deformation of
$(\mathfrak {Q}, \gamma )$
be a deformation of
![]() $\mathcal {Q}$
over R. Let
$\mathcal {Q}$
over R. Let
![]() $h \colon R \to R'$
be a morphism in
$h \colon R \to R'$
be a morphism in
![]() $\mathcal {C}_{\mathcal O}$
. Then the base change
$\mathcal {C}_{\mathcal O}$
. Then the base change
![]() $h^*\mathfrak {Q}$
with the isomorphism
$h^*\mathfrak {Q}$
with the isomorphism
![]() $ \gamma \colon (h^*\mathfrak {Q})_{({\mathcal O}, (\pi ))} = \mathfrak {Q}_{({\mathcal O}, (\pi ))} \overset {\sim }{\to } \mathcal {Q} $
is a deformation of
$ \gamma \colon (h^*\mathfrak {Q})_{({\mathcal O}, (\pi ))} = \mathfrak {Q}_{({\mathcal O}, (\pi ))} \overset {\sim }{\to } \mathcal {Q} $
is a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R'$
.
$R'$
.
Definition 4.1.3 (Universal deformation).
Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. Let
$({\mathcal O}, (\pi ))$
. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. We say that a deformation
$R \in \mathcal {C}_{\mathcal O}$
. We say that a deformation
![]() $(\mathfrak {Q}, \gamma )$
of
$(\mathfrak {Q}, \gamma )$
of
![]() $\mathcal {Q}$
over R is a universal deformation if it satisfies the following property:
$\mathcal {Q}$
over R is a universal deformation if it satisfies the following property:
-
 $(\ast )$
Let
$(\ast )$
Let
 $R' \in \mathcal {C}_{\mathcal O}$
and let
$R' \in \mathcal {C}_{\mathcal O}$
and let
 $(\mathfrak {Q}', \gamma ')$
be a deformation of
$(\mathfrak {Q}', \gamma ')$
be a deformation of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $R'$
. Then there exists a unique local homomorphism
$R'$
. Then there exists a unique local homomorphism
 $ h \colon R \to R' $
over
$ h \colon R \to R' $
over
 ${\mathcal O}$
such that
${\mathcal O}$
such that
 $(h^*\mathfrak {Q}, \gamma )$
is isomorphic to
$(h^*\mathfrak {Q}, \gamma )$
is isomorphic to
 $(\mathfrak {Q}', \gamma ')$
as a deformation of
$(\mathfrak {Q}', \gamma ')$
as a deformation of
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $R'$
.
$R'$
.
In order to state our main results, we need to introduce some more notation. We consider a map
![]() $f \colon (A', I') \to (A, I)$
of orientable and bounded
$f \colon (A', I') \to (A, I)$
of orientable and bounded
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $f \colon A' \to A$
is surjective. Let
$f \colon A' \to A$
is surjective. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
and let
$R \in \mathcal {C}_{\mathcal O}$
and let
![]() $ \mathfrak {Q} $
be a prismatic G-
$ \mathfrak {Q} $
be a prismatic G-
![]() $\mu $
-display over R. Given a homomorphism
$\mu $
-display over R. Given a homomorphism
![]() $g \colon R \to A/I$
over
$g \colon R \to A/I$
over
![]() ${\mathcal O}$
, we can regard
${\mathcal O}$
, we can regard
![]() $(A, I)$
as an object of
$(A, I)$
as an object of ![]() , and we have the associated G-
, and we have the associated G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}_{g}=\mathfrak {Q}_{(A, I)}$
over
$\mathfrak {Q}_{g}=\mathfrak {Q}_{(A, I)}$
over
![]() $(A, I)$
. Let
$(A, I)$
. Let
be the set of homomorphisms
![]() $g' \colon R \to A'/I'$
over
$g' \colon R \to A'/I'$
over
![]() ${\mathcal O}$
which are lifts of g. For each
${\mathcal O}$
which are lifts of g. For each
![]() $g' \in {\mathrm {Hom}} (R, A'/I')_{g}$
, the G-
$g' \in {\mathrm {Hom}} (R, A'/I')_{g}$
, the G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathfrak {Q}_{g'}$
over
$\mathfrak {Q}_{g'}$
over
![]() $(A', I')$
is equipped with the isomorphism
$(A', I')$
is equipped with the isomorphism
![]() $ \gamma _f \colon f^*(\mathfrak {Q}_{g'}) \overset {\sim }{\to } \mathfrak {Q}_{g}; $
namely, it is a deformation of
$ \gamma _f \colon f^*(\mathfrak {Q}_{g'}) \overset {\sim }{\to } \mathfrak {Q}_{g}; $
namely, it is a deformation of
![]() $\mathfrak {Q}_{g}$
. In conclusion, we have a map
$\mathfrak {Q}_{g}$
. In conclusion, we have a map
of sets. We call
![]() $ {\mathrm {ev}} _{\mathfrak {Q}}$
the evaluation map.
$ {\mathrm {ev}} _{\mathfrak {Q}}$
the evaluation map.
Example 4.1.4. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. Let
$({\mathcal O}, (\pi ))$
. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
and let
$R \in \mathcal {C}_{\mathcal O}$
and let
![]() $ \mathfrak {Q} $
be a deformation of
$ \mathfrak {Q} $
be a deformation of
![]() $\mathcal {Q}$
over R. We consider the nilpotent thickening
$\mathcal {Q}$
over R. We consider the nilpotent thickening
of Breuil–Kisin type. By the above construction, we have a map
The set
![]() $ {\mathrm {Hom}} (R, k[[t]]/t^2)_{e}$
can be naturally identified with the tangent space
$ {\mathrm {Hom}} (R, k[[t]]/t^2)_{e}$
can be naturally identified with the tangent space
![]() $\mathfrak {t}_{R}$
of R over
$\mathfrak {t}_{R}$
of R over
![]() ${\mathcal O}$
(cf. Remark 3.4.7). We write
${\mathcal O}$
(cf. Remark 3.4.7). We write
for the above map
![]() $ {\mathrm {ev}} _{\mathfrak {Q}}$
.
$ {\mathrm {ev}} _{\mathfrak {Q}}$
.
Definition 4.1.5 (Kodaira–Spencer map).
The map
![]() $ {\mathrm {KS}} (\mathfrak {Q})$
defined in Example 4.1.4 is called the Kodaira–Spencer map of
$ {\mathrm {KS}} (\mathfrak {Q})$
defined in Example 4.1.4 is called the Kodaira–Spencer map of
![]() $\mathfrak {Q}$
. We say that
$\mathfrak {Q}$
. We say that
![]() $\mathfrak {Q}$
is versal if the Kodaira–Spencer map
$\mathfrak {Q}$
is versal if the Kodaira–Spencer map
![]() $ {\mathrm {KS}} (\mathfrak {Q})$
is surjective.
$ {\mathrm {KS}} (\mathfrak {Q})$
is surjective.
Definition 4.1.6. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
and let
$R \in \mathcal {C}_{\mathcal O}$
and let
![]() $ \mathfrak {Q} $
be a prismatic G-
$ \mathfrak {Q} $
be a prismatic G-
![]() $\mu $
-display over R. We say that
$\mu $
-display over R. We say that
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
![]() $(\mathrm {Perfd})$
if it satisfies the following condition:
$(\mathrm {Perfd})$
if it satisfies the following condition:
-
 $(\ast )$
Let
$(\ast )$
Let
 $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
 ${\mathcal O}$
. Let
${\mathcal O}$
. Let
 $e \colon R \to S/a$
be the composition
$e \colon R \to S/a$
be the composition
 $R \to k \to S/a$
. Then the evaluation map is bijective for any
$R \to k \to S/a$
. Then the evaluation map is bijective for any $$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R, S/a^{m})_{e} \to {\mathrm{Def}}(\mathfrak{Q}_e)_{(W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m}, I_S)} \end{align*}$$
$$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R, S/a^{m})_{e} \to {\mathrm{Def}}(\mathfrak{Q}_e)_{(W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m}, I_S)} \end{align*}$$
 $m \geq 1$
.
$m \geq 1$
.
We say that
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
![]() $(\mathrm {BK})$
if it satisfies the following condition:
$(\mathrm {BK})$
if it satisfies the following condition:
-
 $(\ast )$
Let
$(\ast )$
Let
 $\widetilde {k}$
be a perfect field containing k. We set
$\widetilde {k}$
be a perfect field containing k. We set
 $\widetilde {{\mathcal O}}:=W(\widetilde {k}) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E$
. Let
$\widetilde {{\mathcal O}}:=W(\widetilde {k}) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E$
. Let
 $(\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E}))$
be an
$(\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E}))$
be an
 ${\mathcal O}_E$
-prism of Breuil–Kisin type over
${\mathcal O}_E$
-prism of Breuil–Kisin type over
 $\widetilde {{\mathcal O}}$
, where
$\widetilde {{\mathcal O}}$
, where
 $\mathfrak {S}_{\widetilde {{\mathcal O}}}=\widetilde {{\mathcal O}}[[t_1, \dotsc , n]]$
for an integer
$\mathfrak {S}_{\widetilde {{\mathcal O}}}=\widetilde {{\mathcal O}}[[t_1, \dotsc , n]]$
for an integer
 $n \geq 0$
. We set
$n \geq 0$
. We set
 $\widetilde {R}:=\mathfrak {S}_{\widetilde {{\mathcal O}}}/\mathcal {E}$
and
$\widetilde {R}:=\mathfrak {S}_{\widetilde {{\mathcal O}}}/\mathcal {E}$
and
 $\widetilde {R}_m:=\widetilde {R}/\mathfrak {m}^{m}_{\widetilde {R}}=\mathfrak {S}_{\widetilde {{\mathcal O}}, m}/\mathcal {E}$
for an integer
$\widetilde {R}_m:=\widetilde {R}/\mathfrak {m}^{m}_{\widetilde {R}}=\mathfrak {S}_{\widetilde {{\mathcal O}}, m}/\mathcal {E}$
for an integer
 $m \geq 1$
. Let
$m \geq 1$
. Let
 $e \colon R \to \widetilde {k}$
be the natural homomorphism. Then the evaluation map is bijective for any
$e \colon R \to \widetilde {k}$
be the natural homomorphism. Then the evaluation map is bijective for any $$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R, \widetilde{R}_m)_{e} \to {\mathrm{Def}}(\mathfrak{Q}_e)_{(\mathfrak{S}_{\widetilde{{\mathcal O}}, m}, (\mathcal{E}))} \end{align*}$$
$$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R, \widetilde{R}_m)_{e} \to {\mathrm{Def}}(\mathfrak{Q}_e)_{(\mathfrak{S}_{\widetilde{{\mathcal O}}, m}, (\mathcal{E}))} \end{align*}$$
 $m \geq 1$
.
$m \geq 1$
.
The goal of this section is to prove the following two results. The first one is about the existence of universal deformations and their properties. Recall that
![]() $R_{G, \mu }$
is the completion of
$R_{G, \mu }$
is the completion of
![]() ${\mathcal O}_{U^{-}_{\mu }, 1}$
with respect to the maximal ideal; see Definition 3.4.3. There exists an isomorphism
${\mathcal O}_{U^{-}_{\mu }, 1}$
with respect to the maximal ideal; see Definition 3.4.3. There exists an isomorphism
![]() $R_{G, \mu } \simeq {\mathcal O}[[t_1, \dotsc , t_r]]$
over
$R_{G, \mu } \simeq {\mathcal O}[[t_1, \dotsc , t_r]]$
over
![]() ${\mathcal O}$
, so that
${\mathcal O}$
, so that
![]() $R_{G, \mu } \in \mathcal {C}_{\mathcal O}$
.
$R_{G, \mu } \in \mathcal {C}_{\mathcal O}$
.
Theorem 4.1.7. Assume that
![]() $\mu $
is 1-bounded. For a G-
$\mu $
is 1-bounded. For a G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $({\mathcal O}, (\pi ))$
, there exists a universal deformation
$({\mathcal O}, (\pi ))$
, there exists a universal deformation
![]() $(\mathfrak {Q}^{ {\mathrm {univ}} }, \gamma )$
of
$(\mathfrak {Q}^{ {\mathrm {univ}} }, \gamma )$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
. Moreover,
$R_{G, \mu }$
. Moreover,
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
has the properties
$\mathfrak {Q}^{ {\mathrm {univ}} }$
has the properties
![]() $(\mathrm {Perfd})$
and
$(\mathrm {Perfd})$
and
![]() $(\mathrm {BK})$
. In particular,
$(\mathrm {BK})$
. In particular,
![]() $(\mathfrak {Q}^{ {\mathrm {univ}} }, \gamma )$
is versal.
$(\mathfrak {Q}^{ {\mathrm {univ}} }, \gamma )$
is versal.
The second one gives some characterizations of universal deformations. Let
![]() ${\mathcal O}_C$
be the
${\mathcal O}_C$
be the
![]() $\pi $
-adic completion of the integral closure of
$\pi $
-adic completion of the integral closure of
![]() ${\mathcal O}$
in an algebraic closure of
${\mathcal O}$
in an algebraic closure of
![]() ${\mathcal O}[1/\pi ]$
. Then
${\mathcal O}[1/\pi ]$
. Then
![]() ${\mathcal O}_C$
is a
${\mathcal O}_C$
is a
![]() $\pi $
-adically complete valuation ring of rank
$\pi $
-adically complete valuation ring of rank
![]() $1$
with algebraically closed fraction field. We note that
$1$
with algebraically closed fraction field. We note that
![]() ${\mathcal O}_C$
is a perfectoid ring. We denote by
${\mathcal O}_C$
is a perfectoid ring. We denote by
![]() ${\mathcal O}_{C^\flat }$
the tilt of
${\mathcal O}_{C^\flat }$
the tilt of
![]() ${\mathcal O}_C$
. There is an element
${\mathcal O}_C$
. There is an element
![]() $\pi ^\flat \in {\mathcal O}_{C^\flat }$
with
$\pi ^\flat \in {\mathcal O}_{C^\flat }$
with
![]() $\theta ([\pi ^\flat ])=\pi $
, so that
$\theta ([\pi ^\flat ])=\pi $
, so that
![]() $({\mathcal O}_C, \pi ^\flat )$
is a perfectoid pair over
$({\mathcal O}_C, \pi ^\flat )$
is a perfectoid pair over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Theorem 4.1.8. Assume that
![]() $\mu $
is 1-bounded. Let
$\mu $
is 1-bounded. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. Let
$({\mathcal O}, (\pi ))$
. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
and let
$R \in \mathcal {C}_{\mathcal O}$
and let
![]() $(\mathfrak {Q}, \gamma )$
be a deformation of
$(\mathfrak {Q}, \gamma )$
be a deformation of
![]() $\mathcal {Q}$
over R. Then the following statements are equivalent:
$\mathcal {Q}$
over R. Then the following statements are equivalent:
-
(1)
 $(\mathfrak {Q}, \gamma )$
is a universal deformation.
$(\mathfrak {Q}, \gamma )$
is a universal deformation. -
(2)
 $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
 $(\mathrm {BK})$
.
$(\mathrm {BK})$
. -
(3)
 $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
 $(\mathrm {Perfd})$
.
$(\mathrm {Perfd})$
. -
(4) Let
 $e \colon R \to {\mathcal O}_C/\pi $
be the composition
$e \colon R \to {\mathcal O}_C/\pi $
be the composition
 $R \to k \to {\mathcal O}_C/\pi $
. The evaluation map is bijective.
$R \to k \to {\mathcal O}_C/\pi $
. The evaluation map is bijective. $$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R, {\mathcal O}_C/\pi^{2})_{e} \to {\mathrm{Def}}(\mathfrak{Q}_e)_{(W_{{\mathcal O}_E}({\mathcal O}_{C^\flat})/[\pi^\flat]^{2}, I_{{\mathcal O}_C})} \end{align*}$$
$$\begin{align*}{\mathrm{ev}}_{\mathfrak{Q}} \colon {\mathrm{Hom}}(R, {\mathcal O}_C/\pi^{2})_{e} \to {\mathrm{Def}}(\mathfrak{Q}_e)_{(W_{{\mathcal O}_E}({\mathcal O}_{C^\flat})/[\pi^\flat]^{2}, I_{{\mathcal O}_C})} \end{align*}$$
-
(5) The equalities
 $\dim R=\dim R_{G, \mu }$
and
$\dim R=\dim R_{G, \mu }$
and
 $\dim _k \mathfrak {t}_R=\dim _k \mathfrak {t}_{G, \mu }$
hold, and
$\dim _k \mathfrak {t}_R=\dim _k \mathfrak {t}_{G, \mu }$
hold, and
 $(\mathfrak {Q}, \gamma )$
is versal. (Here,
$(\mathfrak {Q}, \gamma )$
is versal. (Here,
 $\dim R$
is the dimension of the ring R and
$\dim R$
is the dimension of the ring R and
 $\dim _k \mathfrak {t}_R$
is the dimension of the k-vector space
$\dim _k \mathfrak {t}_R$
is the dimension of the k-vector space
 $\mathfrak {t}_R$
.)
$\mathfrak {t}_R$
.)
The rest of this section is devoted to the proofs of Theorem 4.1.7 and Theorem 4.1.8. In Section 4.2, we present a few technical results on maps of
![]() ${\mathcal O}_E$
-prisms. In Section 4.3, we investigate the relation between
${\mathcal O}_E$
-prisms. In Section 4.3, we investigate the relation between
![]() $\mathrm {(Perfd)}$
,
$\mathrm {(Perfd)}$
,
![]() $\mathrm {(BK)}$
and the property of being a universal deformation. For this, we discuss the linearity of evaluation maps, which plays an important role in our discussion. Finally, in Section 4.4, we complete the proofs of Theorem 4.1.7 and Theorem 4.1.8.
$\mathrm {(BK)}$
and the property of being a universal deformation. For this, we discuss the linearity of evaluation maps, which plays an important role in our discussion. Finally, in Section 4.4, we complete the proofs of Theorem 4.1.7 and Theorem 4.1.8.
4.2 Preliminaries on maps of
 ${\mathcal O}_E$
-prisms
${\mathcal O}_E$
-prisms
Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. We fix an
$R \in \mathcal {C}_{\mathcal O}$
. We fix an
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $ (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) $
of Breuil–Kisin type, where
$ (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) $
of Breuil–Kisin type, where
![]() $\mathfrak {S}_{\mathcal O}={\mathcal O}[[t_1, \dotsc , t_n]]$
, with an isomorphism
$\mathfrak {S}_{\mathcal O}={\mathcal O}[[t_1, \dotsc , t_n]]$
, with an isomorphism
![]() $R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E}$
over
$R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E}$
over
![]() ${\mathcal O}$
. We note that R is of dimension n. (Here, n is allowed to be zero.)
${\mathcal O}$
. We note that R is of dimension n. (Here, n is allowed to be zero.)
Let
![]() $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $m \geq 1$
be an integer. The following notion of primitive map will play an important role in our proof of Theorem 4.1.7.
$m \geq 1$
be an integer. The following notion of primitive map will play an important role in our proof of Theorem 4.1.7.
Definition 4.2.1 (Primitive map).
A map
of
![]() ${\mathcal O}_E$
-prisms over
${\mathcal O}_E$
-prisms over
![]() ${\mathcal O}$
is called primitive with respect to
${\mathcal O}$
is called primitive with respect to
![]() $a^\flat $
(or simply, primitive) if for every
$a^\flat $
(or simply, primitive) if for every
![]() $1 \leq i \leq n$
, the map f sends
$1 \leq i \leq n$
, the map f sends
![]() $t_i$
to
$t_i$
to
![]() $[a^\flat b^\flat _i]$
for some element
$[a^\flat b^\flat _i]$
for some element
![]() $b^\flat _i \in S^\flat $
. (Here, we denote the image of
$b^\flat _i \in S^\flat $
. (Here, we denote the image of
![]() $[a^\flat b^\flat _i] \in W_{{\mathcal O}_E}(S^\flat )$
in
$[a^\flat b^\flat _i] \in W_{{\mathcal O}_E}(S^\flat )$
in
![]() $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
by the same symbol.)
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
by the same symbol.)
We note that a primitive map
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
factors through a map
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
factors through a map
![]() $(\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
.
$(\mathfrak {S}_{{\mathcal O}, m}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S)$
.
Lemma 4.2.2. Assume that the map
![]() $S \to S$
,
$S \to S$
,
![]() $x \mapsto x^p$
is surjective. Then, for a homomorphism
$x \mapsto x^p$
is surjective. Then, for a homomorphism
![]() $g \colon R \to S/a^m$
over
$g \colon R \to S/a^m$
over
![]() ${\mathcal O}$
which is a lift of the composition
${\mathcal O}$
which is a lift of the composition
![]() $R \to k \to S/a$
, there exists a primitive map
$R \to k \to S/a$
, there exists a primitive map
![]() $ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
which induces g.
$ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
which induces g.
Proof. For every
![]() $1 \leq i \leq n$
, the image of
$1 \leq i \leq n$
, the image of
![]() $t_i$
under the composition
$t_i$
under the composition
![]() $\mathfrak {S}_{\mathcal O} \to R \to S/a^m$
can be written as
$\mathfrak {S}_{\mathcal O} \to R \to S/a^m$
can be written as
![]() $a b_i$
for some element
$a b_i$
for some element
![]() $b_i \in S$
. (Again, we abuse notation and denote the image of
$b_i \in S$
. (Again, we abuse notation and denote the image of
![]() $a b_i \in S$
in
$a b_i \in S$
in
![]() $S/a^m$
by the same symbol.) Since the map
$S/a^m$
by the same symbol.) Since the map
![]() $S \to S$
,
$S \to S$
,
![]() $x \mapsto x^p$
is surjective, there exists an element
$x \mapsto x^p$
is surjective, there exists an element
![]() $b^\flat _i \in S^\flat $
with
$b^\flat _i \in S^\flat $
with
![]() $\theta ([b^\flat _i])=b_i$
(cf. [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.3]). We define a homomorphism
$\theta ([b^\flat _i])=b_i$
(cf. [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.3]). We define a homomorphism
![]() $f \colon \mathfrak {S}_{\mathcal O} \to W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
over
$f \colon \mathfrak {S}_{\mathcal O} \to W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
over
![]() ${\mathcal O}$
by
${\mathcal O}$
by
![]() $t_i \mapsto [a^\flat b^\flat _i]$
. Since
$t_i \mapsto [a^\flat b^\flat _i]$
. Since
![]() $\phi ([a^\flat b^\flat _i])=[a^\flat b^\flat _i]^q$
, it follows that f is
$\phi ([a^\flat b^\flat _i])=[a^\flat b^\flat _i]^q$
, it follows that f is
![]() $\phi $
-equivariant, which in turn implies that f is a homomorphism of
$\phi $
-equivariant, which in turn implies that f is a homomorphism of
![]() $\delta _E$
-rings since both the target and the source are
$\delta _E$
-rings since both the target and the source are
![]() $\pi $
-torsion free (see Lemma 2.1.2). By construction, we see that f is a lift of g. In particular, f sends
$\pi $
-torsion free (see Lemma 2.1.2). By construction, we see that f is a lift of g. In particular, f sends
![]() $\mathcal {E}$
into the kernel of
$\mathcal {E}$
into the kernel of
![]() $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m \to S/a^m$
. Thus, we have a primitive map
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m \to S/a^m$
. Thus, we have a primitive map
![]() $ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
which induces g.
$ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
which induces g.
Remark 4.2.3. Any perfectoid ring S admits a p-completely faithfully flat homomorphism
![]() $S \to S'$
of perfectoid rings such that the map
$S \to S'$
of perfectoid rings such that the map
![]() $S' \to S'$
,
$S' \to S'$
,
![]() $x \mapsto x^p$
is surjective. This is a consequence of André’s flatness lemma; see [Reference Bhatt and ScholzeBS22, Theorem 7.14].
$x \mapsto x^p$
is surjective. This is a consequence of André’s flatness lemma; see [Reference Bhatt and ScholzeBS22, Theorem 7.14].
Lemma 4.2.4. Let
![]() $ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
be a primitive map and let
$ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m, I_S) $
be a primitive map and let
![]() $g \colon R \to S/a^m$
be the induced homomorphism. Suppose that we are given a homomorphism
$g \colon R \to S/a^m$
be the induced homomorphism. Suppose that we are given a homomorphism
![]() $g' \colon R \to S/a^{m+1}$
over
$g' \colon R \to S/a^{m+1}$
over
![]() ${\mathcal O}$
which is a lift of g. Then there exists a map
${\mathcal O}$
which is a lift of g. Then there exists a map
![]() $ f' \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}, I_S) $
which induces f and
$ f' \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}, I_S) $
which induces f and
![]() $g'$
.
$g'$
.
Proof. Since f is primitive, it maps
![]() $t_i$
to
$t_i$
to
![]() $[a^\flat b^\flat _i] \in W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
for some element
$[a^\flat b^\flat _i] \in W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^m$
for some element
![]() $b^\flat _i \in S^\flat $
for any i. Let
$b^\flat _i \in S^\flat $
for any i. Let
![]() $b_i:=\theta ([b^\flat _i]) \in S$
. The image of
$b_i:=\theta ([b^\flat _i]) \in S$
. The image of
![]() $t_i$
under the composition
$t_i$
under the composition
![]() $\mathfrak {S}_{\mathcal O} \to R \to S/a^{m+1}$
can be written as
$\mathfrak {S}_{\mathcal O} \to R \to S/a^{m+1}$
can be written as
![]() $ab_i+a^m y_i$
for some element
$ab_i+a^m y_i$
for some element
![]() $y_i \in S/a^{m+1}$
. Let
$y_i \in S/a^{m+1}$
. Let
![]() $x_i \in W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}$
be such that
$x_i \in W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}$
be such that
![]() $\theta _{{\mathcal O}_E}(x_i)=y_i$
in
$\theta _{{\mathcal O}_E}(x_i)=y_i$
in
![]() $S/a^{m+1}$
. We define a homomorphism
$S/a^{m+1}$
. We define a homomorphism
![]() $f' \colon \mathfrak {S}_{\mathcal O} \to W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}$
over
$f' \colon \mathfrak {S}_{\mathcal O} \to W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}$
over
![]() ${\mathcal O}$
by
${\mathcal O}$
by
![]() $t_i \mapsto [a^\flat b^\flat _i]+[a^\flat ]^m x_i$
. By construction, it is a lift of
$t_i \mapsto [a^\flat b^\flat _i]+[a^\flat ]^m x_i$
. By construction, it is a lift of
![]() $g'$
. We claim that
$g'$
. We claim that
![]() $f'$
is a homomorphism of
$f'$
is a homomorphism of
![]() $\delta _E$
-rings. Indeed, we have
$\delta _E$
-rings. Indeed, we have
in
![]() $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}$
since
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}$
since
![]() $qm \geq m+1$
. Similarly, we have
$qm \geq m+1$
. Similarly, we have
![]() $ ([a^\flat b^\flat _i]+[a^\flat ]^m x_i)^q=[a^\flat b^\flat _i]^q. $
It follows that
$ ([a^\flat b^\flat _i]+[a^\flat ]^m x_i)^q=[a^\flat b^\flat _i]^q. $
It follows that
![]() $f'$
is
$f'$
is
![]() $\phi $
-equivariant, which in turn implies that it is a homomorphism of
$\phi $
-equivariant, which in turn implies that it is a homomorphism of
![]() $\delta _E$
-rings. The resulting map
$\delta _E$
-rings. The resulting map
![]() $ f' \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}, I_S) $
has the desired properties.
$ f' \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1}, I_S) $
has the desired properties.
Lemma 4.2.5. Assume that k is algebraically closed. Let
![]() $m \geq 1$
be an integer and
$m \geq 1$
be an integer and
![]() $x \in \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R$
a nonzero element. Then there exists a complete regular local ring
$x \in \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R$
a nonzero element. Then there exists a complete regular local ring
![]() $R'$
of dimension
$R'$
of dimension
![]() $1$
with a surjection
$1$
with a surjection
![]() $R \to R'$
such that the induced homomorphism
$R \to R'$
such that the induced homomorphism
![]() $ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to \mathfrak {m}^m_{R'}/\mathfrak {m}^{m+1}_{R'} $
sends x to a nonzero element.
$ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to \mathfrak {m}^m_{R'}/\mathfrak {m}^{m+1}_{R'} $
sends x to a nonzero element.
Proof. Let
![]() $x_1, \dotsc , x_n \in \mathfrak {m}_R$
be a regular system of parameters. The homomorphism of graded k-algebras
$x_1, \dotsc , x_n \in \mathfrak {m}_R$
be a regular system of parameters. The homomorphism of graded k-algebras
defined by
![]() $x_i \mapsto x_i \in \mathfrak {m}_R/\mathfrak {m}^{2}_R$
is an isomorphism. Since
$x_i \mapsto x_i \in \mathfrak {m}_R/\mathfrak {m}^{2}_R$
is an isomorphism. Since
![]() $\mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R$
is nonzero, we have
$\mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R$
is nonzero, we have
![]() $n \geq 1$
. If
$n \geq 1$
. If
![]() $n = 1$
, then the assertion holds trivially. We assume that
$n = 1$
, then the assertion holds trivially. We assume that
![]() $n \geq 2$
.
$n \geq 2$
.
We claim that, for a nonzero homogeneous polynomial
![]() $f(x_1, \dotsc , x_n)$
of degree m, there exist two distinct integers
$f(x_1, \dotsc , x_n)$
of degree m, there exist two distinct integers
![]() $i, j \in \{ 1, \dotsc , n \}$
and an element
$i, j \in \{ 1, \dotsc , n \}$
and an element
![]() $b \in k$
such that the image of
$b \in k$
such that the image of
![]() $f(x_1, \dotsc , x_n)$
in
$f(x_1, \dotsc , x_n)$
in
![]() $k[x_1, \dotsc , x_n]/(x_i-bx_j)$
is nonzero. Indeed, since k is infinite, there is a nonzero element
$k[x_1, \dotsc , x_n]/(x_i-bx_j)$
is nonzero. Indeed, since k is infinite, there is a nonzero element
![]() $(b_1, \dotsc , b_n) \in k^n$
such that
$(b_1, \dotsc , b_n) \in k^n$
such that
![]() $f(b_1, \dotsc , b_n) \neq 0$
. Without loss of generality, we may assume that
$f(b_1, \dotsc , b_n) \neq 0$
. Without loss of generality, we may assume that
![]() $b_{n-1} \neq 0$
. We set
$b_{n-1} \neq 0$
. We set
![]() $b:=b_n/b_{n-1}$
. Then the polynomial
$b:=b_n/b_{n-1}$
. Then the polynomial
![]() $f(x_1, \dotsc , x_{n-1}, bx_{n-1}) \in k[x_1, \dotsc , x_{n-1}]$
is nonzero since its evaluation at
$f(x_1, \dotsc , x_{n-1}, bx_{n-1}) \in k[x_1, \dotsc , x_{n-1}]$
is nonzero since its evaluation at
![]() $(b_1, \dotsc , b_{n-1})$
is nonzero.
$(b_1, \dotsc , b_{n-1})$
is nonzero.
The claim implies that there exist two distinct integers
![]() $i, j \in \{ 1, \dotsc , n \}$
and an element
$i, j \in \{ 1, \dotsc , n \}$
and an element
![]() $b \in R$
such that, for the quotient
$b \in R$
such that, for the quotient
![]() $R":=R/(x_i-bx_j)$
, the induced homomorphism
$R":=R/(x_i-bx_j)$
, the induced homomorphism
![]() $ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to \mathfrak {m}^m_{R"}/\mathfrak {m}^{m+1}_{R"} $
sends x to a nonzero element. Since
$ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to \mathfrak {m}^m_{R"}/\mathfrak {m}^{m+1}_{R"} $
sends x to a nonzero element. Since
![]() $R"$
is regular, the assertion follows by repeating this procedure.
$R"$
is regular, the assertion follows by repeating this procedure.
Corollary 4.2.6. Let
![]() $m \geq 1$
be an integer and
$m \geq 1$
be an integer and
![]() $x \in \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R$
a nonzero element. Then there exists a perfectoid pair
$x \in \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R$
a nonzero element. Then there exists a perfectoid pair
![]() $(V, a^\flat )$
over
$(V, a^\flat )$
over
![]() ${\mathcal O}$
with the following properties:
${\mathcal O}$
with the following properties:
-
(1) V is a
 $\pi $
-adically complete valuation ring of rank
$\pi $
-adically complete valuation ring of rank
 $1$
with algebraically closed fraction field.
$1$
with algebraically closed fraction field. -
(2) There exists a primitive map
such that the induced homomorphism $$\begin{align*}(\mathfrak{S}_{\mathcal O}, (\mathcal{E})) \to (W_{{\mathcal O}_E}(V^\flat)/[a^\flat]^{m+1}, I_V) \end{align*}$$
$$\begin{align*}(\mathfrak{S}_{\mathcal O}, (\mathcal{E})) \to (W_{{\mathcal O}_E}(V^\flat)/[a^\flat]^{m+1}, I_V) \end{align*}$$
 $ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to a^mV/a^{m+1}V $
sends x to a nonzero element.
$ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to a^mV/a^{m+1}V $
sends x to a nonzero element.
Proof. We may assume that k is algebraically closed. By Lemma 4.2.5, there exists a complete regular local ring
![]() $R'$
of dimension
$R'$
of dimension
![]() $1$
with a surjection
$1$
with a surjection
![]() $R \to R'$
such that the induced homomorphism
$R \to R'$
such that the induced homomorphism
![]() $ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to \mathfrak {m}^m_{R'}/\mathfrak {m}^{m+1}_{R'} $
sends x to a nonzero element.
$ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to \mathfrak {m}^m_{R'}/\mathfrak {m}^{m+1}_{R'} $
sends x to a nonzero element.
Let
![]() $a \in \mathfrak {m}_{R'}$
be a uniformizer. Let V be the
$a \in \mathfrak {m}_{R'}$
be a uniformizer. Let V be the
![]() $\pi $
-adic completion of the integral closure of
$\pi $
-adic completion of the integral closure of
![]() $R'$
in an algebraic closure of
$R'$
in an algebraic closure of
![]() $R'[1/a]$
. Then V is a
$R'[1/a]$
. Then V is a
![]() $\pi $
-adically complete valuation ring of rank
$\pi $
-adically complete valuation ring of rank
![]() $1$
with algebraically closed fraction field. The natural homomorphism
$1$
with algebraically closed fraction field. The natural homomorphism
![]() $g \colon R \to V/a^{m+1}V$
sends
$g \colon R \to V/a^{m+1}V$
sends
![]() $\mathfrak {m}_R$
into
$\mathfrak {m}_R$
into
![]() $(a)$
, and the induced homomorphism
$(a)$
, and the induced homomorphism
![]() $ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to a^mV/a^{m+1}V $
sends x to a nonzero element. There exists an element
$ \mathfrak {m}^m_R/\mathfrak {m}^{m+1}_R \to a^mV/a^{m+1}V $
sends x to a nonzero element. There exists an element
![]() $a^\flat \in V^\flat $
with
$a^\flat \in V^\flat $
with
![]() $\theta ([a^\flat ])=a$
, so that
$\theta ([a^\flat ])=a$
, so that
![]() $(V, a^\flat )$
is a perfectoid pair over
$(V, a^\flat )$
is a perfectoid pair over
![]() ${\mathcal O}$
. By Lemma 4.2.2, there exists a primitive map
${\mathcal O}$
. By Lemma 4.2.2, there exists a primitive map
![]() $ (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(V^\flat )/[a^\flat ]^{m+1}, I_V) $
which induces g. This concludes the proof.
$ (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(V^\flat )/[a^\flat ]^{m+1}, I_V) $
which induces g. This concludes the proof.
4.3 Linearity of evaluation maps
Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. For deformations of
$({\mathcal O}, (\pi ))$
. For deformations of
![]() $\mathcal {Q}$
, we investigate the relation between
$\mathcal {Q}$
, we investigate the relation between
![]() $\mathrm {(Perfd)}$
,
$\mathrm {(Perfd)}$
,
![]() $\mathrm {(BK)}$
, and the property of being a universal deformation.
$\mathrm {(BK)}$
, and the property of being a universal deformation.
We first note the following consequence of Theorem 2.6.5.
Remark 4.3.1. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. We choose an
$R \in \mathcal {C}_{\mathcal O}$
. We choose an
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type, where
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type, where
![]() $\mathfrak {S}_{\mathcal O}={\mathcal O}[[t_1, \dotsc , t_n]]$
, with an isomorphism
$\mathfrak {S}_{\mathcal O}={\mathcal O}[[t_1, \dotsc , t_n]]$
, with an isomorphism
![]() $R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E}$
over
$R \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E}$
over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to ({\mathcal O}, (\pi )) $
be the morphism defined by
$ f \colon (\mathfrak {S}_{\mathcal O}, (\mathcal {E})) \to ({\mathcal O}, (\pi )) $
be the morphism defined by
![]() $t_i \mapsto 0$
. For a deformation
$t_i \mapsto 0$
. For a deformation
![]() $\mathfrak {Q}$
of
$\mathfrak {Q}$
of
![]() $\mathcal {Q}$
over R, the value
$\mathcal {Q}$
over R, the value
![]() $\mathfrak {Q}_{(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))}$
is naturally a deformation of
$\mathfrak {Q}_{(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))}$
is naturally a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
. By Theorem 2.6.5, this construction induces an equivalence from the groupoid of deformations of
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
. By Theorem 2.6.5, this construction induces an equivalence from the groupoid of deformations of
![]() $\mathcal {Q}$
over R to that of deformations of
$\mathcal {Q}$
over R to that of deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
.
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
.
Corollary 4.3.2. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
. There is at most one isomorphism between two deformations of
$R \in \mathcal {C}_{\mathcal O}$
. There is at most one isomorphism between two deformations of
![]() $\mathcal {Q}$
over R.
$\mathcal {Q}$
over R.
Corollary 4.3.3. Let
![]() $R \in \mathcal {C}_{\mathcal O}$
and let
$R \in \mathcal {C}_{\mathcal O}$
and let
![]() $\mathfrak {Q}$
be a deformation of
$\mathfrak {Q}$
be a deformation of
![]() $\mathcal {Q}$
over R. If
$\mathcal {Q}$
over R. If
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
![]() $\mathrm {(BK)}$
, then
$\mathrm {(BK)}$
, then
![]() $\mathfrak {Q}$
is a universal deformation of
$\mathfrak {Q}$
is a universal deformation of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Proof. Let
![]() $R' \in \mathcal {C}_{\mathcal O}$
and let
$R' \in \mathcal {C}_{\mathcal O}$
and let
![]() $\mathfrak {Q}'$
be a deformation of
$\mathfrak {Q}'$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R'$
. We want to show that there exists a unique local homomorphism
$R'$
. We want to show that there exists a unique local homomorphism
![]() $ h \colon R \to R' $
over
$ h \colon R \to R' $
over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $h^*\mathfrak {Q}$
is isomorphic to
$h^*\mathfrak {Q}$
is isomorphic to
![]() $\mathfrak {Q}'$
as a deformation of
$\mathfrak {Q}'$
as a deformation of
![]() $\mathcal {Q}$
. We fix an
$\mathcal {Q}$
. We fix an
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type with an isomorphism
$(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))$
of Breuil–Kisin type with an isomorphism
![]() $ R' \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E} $
over
$ R' \simeq \mathfrak {S}_{\mathcal O}/\mathcal {E} $
over
![]() ${\mathcal O}$
. By Example 3.1.6 and Corollary 3.2.10, we have
${\mathcal O}$
. By Example 3.1.6 and Corollary 3.2.10, we have
Since
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
![]() $\mathrm {(BK)}$
, we see that the evaluation map
$\mathrm {(BK)}$
, we see that the evaluation map
is bijective. (Here,
![]() $e \colon R \to k$
is the projection.) For a local homomorphism
$e \colon R \to k$
is the projection.) For a local homomorphism
![]() $h \colon R \to R'$
over
$h \colon R \to R'$
over
![]() ${\mathcal O}$
, it follows from Remark 4.3.1 that
${\mathcal O}$
, it follows from Remark 4.3.1 that
![]() $h^*\mathfrak {Q} \simeq \mathfrak {Q}'$
if and only if
$h^*\mathfrak {Q} \simeq \mathfrak {Q}'$
if and only if
![]() $\mathfrak {Q}_h \simeq \mathfrak {Q}^{\prime }_{(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))}$
. Since the above map
$\mathfrak {Q}_h \simeq \mathfrak {Q}^{\prime }_{(\mathfrak {S}_{\mathcal O}, (\mathcal {E}))}$
. Since the above map
![]() $ {\mathrm {ev}} _{\mathfrak {Q}}$
is bijective, such a homomorphism h exists and is unique.
$ {\mathrm {ev}} _{\mathfrak {Q}}$
is bijective, such a homomorphism h exists and is unique.
Remark 4.3.4. If a deformation
![]() $ \mathfrak {Q} $
of
$ \mathfrak {Q} $
of
![]() $\mathcal {Q}$
over R for some
$\mathcal {Q}$
over R for some
![]() $R \in \mathcal {C}_{\mathcal O}$
satisfies the property
$R \in \mathcal {C}_{\mathcal O}$
satisfies the property
![]() $(\mathrm {BK})$
, then the Kodaira–Spencer map
$(\mathrm {BK})$
, then the Kodaira–Spencer map
![]() $ {\mathrm {KS}} (\mathfrak {Q})$
is bijective, so that
$ {\mathrm {KS}} (\mathfrak {Q})$
is bijective, so that
![]() $\mathfrak {Q}$
is versal.
$\mathfrak {Q}$
is versal.
Remark 4.3.5. Assume that there exists a deformation
![]() $\mathfrak {Q}$
of
$\mathfrak {Q}$
of
![]() $\mathcal {Q}$
over R for some
$\mathcal {Q}$
over R for some
![]() $R \in \mathcal {C}_{\mathcal O}$
such that
$R \in \mathcal {C}_{\mathcal O}$
such that
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
![]() $\mathrm {(BK)}$
. It follows from Corollary 4.3.3 that
$\mathrm {(BK)}$
. It follows from Corollary 4.3.3 that
![]() $\mathfrak {Q}$
is a universal deformation. Let
$\mathfrak {Q}$
is a universal deformation. Let
![]() $\mathfrak {Q}'$
be another deformation of
$\mathfrak {Q}'$
be another deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R'$
for some
$R'$
for some
![]() $R' \in \mathcal {C}_{\mathcal O}$
. There exists a unique local homomorphism
$R' \in \mathcal {C}_{\mathcal O}$
. There exists a unique local homomorphism
![]() $ h \colon R \to R' $
over
$ h \colon R \to R' $
over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $h^*\mathfrak {Q} \simeq \mathfrak {Q}'$
by the universal property. For the homomorphism
$h^*\mathfrak {Q} \simeq \mathfrak {Q}'$
by the universal property. For the homomorphism
![]() $ \mathfrak {t}_{R'} \to \mathfrak {t}_{R} $
induced from h, the following diagram commutes:
$ \mathfrak {t}_{R'} \to \mathfrak {t}_{R} $
induced from h, the following diagram commutes:

Since
![]() $ {\mathrm {KS}} (\mathfrak {Q})$
is bijective, we see that
$ {\mathrm {KS}} (\mathfrak {Q})$
is bijective, we see that
![]() $\mathfrak {Q}'$
is versal if and only if
$\mathfrak {Q}'$
is versal if and only if
![]() $\mathfrak {t}_{R'} \to \mathfrak {t}_{R}$
is surjective.
$\mathfrak {t}_{R'} \to \mathfrak {t}_{R}$
is surjective.
To proceed further, we need to introduce two more conditions (Perfd-lin) and (BK-lin).
Remark 4.3.6. We retain the notation from Definition 4.1.6 with
![]() $R=R_{G, \mu }$
. Let
$R=R_{G, \mu }$
. Let
![]() $m \geq 1$
be an integer. Let
$m \geq 1$
be an integer. Let
![]() $g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
. For any
$g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
. For any
![]() $h \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
, the map
$h \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
, the map
defined by
![]() $g' \mapsto g'-h$
is bijective.
$g' \mapsto g'-h$
is bijective.
Similarly, let
![]() $g \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_m)_{e}$
. For any
$g \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_m)_{e}$
. For any
![]() $h \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_{m+1})_{g}$
, we have the following bijection:
$h \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_{m+1})_{g}$
, we have the following bijection:
Definition 4.3.7. We retain the notation of Definition 4.1.6. Let
![]() $ \mathfrak {Q} $
be a prismatic G-
$ \mathfrak {Q} $
be a prismatic G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $R_{G, \mu }$
. We say that
$R_{G, \mu }$
. We say that
![]() $\mathfrak {Q}$
has the property (Perfd-lin) if it satisfies the following condition:
$\mathfrak {Q}$
has the property (Perfd-lin) if it satisfies the following condition:
-
 $(\ast )$
Let
$(\ast )$
Let
 $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
 ${\mathcal O}$
such that
${\mathcal O}$
such that
 $\mathfrak {Q}_e$
is a banal G-
$\mathfrak {Q}_e$
is a banal G-
 $\mu $
-display over
$\mu $
-display over
 $(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ], I_S)$
. Let
$(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ], I_S)$
. Let
 $m \geq 1$
be an integer and let
$m \geq 1$
be an integer and let
 $g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
. Then, for any
$g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
. Then, for any
 $h \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
and any isomorphism
$h \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
and any isomorphism
 $\beta \colon \mathfrak {Q}_g \overset {\sim }{\to } \mathcal {Q}_X$
, the following composition is an
$\beta \colon \mathfrak {Q}_g \overset {\sim }{\to } \mathcal {Q}_X$
, the following composition is an $$ \begin{align*} \begin{split} \mathfrak{t}_{G, \mu} \otimes_k &(a^{m}S/a^{m+1}S) \overset{\mathrm{Diff}^{-1}_{h}}{\longrightarrow} {\mathrm{Hom}}(R_{G, \mu}, S/a^{m+1})_{g} \\ &\overset{{\mathrm{ev}}_{\mathfrak{Q}}}{\longrightarrow} {\mathrm{Def}}(\mathfrak{Q}_g)_{(W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m+1}, I_S)} \overset{{\mathrm{Per}}^{\beta}_{\mathfrak{Q}_h}}{\longrightarrow} \mathfrak{t}_{G, \mu} \otimes_k (a^{m}S/a^{m+1}S) \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathfrak{t}_{G, \mu} \otimes_k &(a^{m}S/a^{m+1}S) \overset{\mathrm{Diff}^{-1}_{h}}{\longrightarrow} {\mathrm{Hom}}(R_{G, \mu}, S/a^{m+1})_{g} \\ &\overset{{\mathrm{ev}}_{\mathfrak{Q}}}{\longrightarrow} {\mathrm{Def}}(\mathfrak{Q}_g)_{(W_{{\mathcal O}_E}(S^\flat)/[a^\flat]^{m+1}, I_S)} \overset{{\mathrm{Per}}^{\beta}_{\mathfrak{Q}_h}}{\longrightarrow} \mathfrak{t}_{G, \mu} \otimes_k (a^{m}S/a^{m+1}S) \end{split} \end{align*} $$
 $S/a$
-linear isomorphism. See Remark 3.4.8 for the normalized period map
$S/a$
-linear isomorphism. See Remark 3.4.8 for the normalized period map
 $ {\mathrm {Per}} ^{\beta }_{\mathfrak {Q}_h}$
, which is bijective by Theorem 3.3.4. The above composition is denoted by
$ {\mathrm {Per}} ^{\beta }_{\mathfrak {Q}_h}$
, which is bijective by Theorem 3.3.4. The above composition is denoted by
 $ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}. $
$ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}. $
We say that
![]() $\mathfrak {Q}$
has the property (BK-lin) if it satisfies the following condition:
$\mathfrak {Q}$
has the property (BK-lin) if it satisfies the following condition:
-
 $(\ast )$
Let
$(\ast )$
Let
 $\widetilde {k}$
be a perfect field containing k such that
$\widetilde {k}$
be a perfect field containing k such that
 $\mathfrak {Q}_{(\widetilde {{\mathcal O}}, (\pi ))}$
is banal. Let
$\mathfrak {Q}_{(\widetilde {{\mathcal O}}, (\pi ))}$
is banal. Let
 $(\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E}))$
be an
$(\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E}))$
be an
 ${\mathcal O}_E$
-prism of Breuil–Kisin type over
${\mathcal O}_E$
-prism of Breuil–Kisin type over
 $\widetilde {{\mathcal O}}$
. Let
$\widetilde {{\mathcal O}}$
. Let
 $m \geq 1$
be an integer and let
$m \geq 1$
be an integer and let
 $g \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_m)_{e}$
. Then, for any
$g \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_m)_{e}$
. Then, for any
 $h \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_{m+1})_{g}$
and any isomorphism
$h \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_{m+1})_{g}$
and any isomorphism
 $\beta \colon \mathfrak {Q}_g \overset {\sim }{\to } \mathcal {Q}_X$
, the following composition is a
$\beta \colon \mathfrak {Q}_g \overset {\sim }{\to } \mathcal {Q}_X$
, the following composition is a $$ \begin{align*} \begin{split} \mathfrak{t}_{G, \mu} \otimes_k &(\mathfrak{m}^{m}_{\widetilde{R}}/\mathfrak{m}^{m+1}_{\widetilde{R}}) \overset{\mathrm{Diff}^{-1}_{h}}{\longrightarrow} {\mathrm{Hom}}(R_{G, \mu}, \widetilde{R}_{m+1})_{g} \\ &\overset{{\mathrm{ev}}_{\mathfrak{Q}}}{\longrightarrow} {\mathrm{Def}}(\mathfrak{Q}_g)_{(\mathfrak{S}_{\widetilde{{\mathcal O}}, m+1}, (\mathcal{E}))} \overset{{\mathrm{Per}}^{\beta}_{\mathfrak{Q}_h}}{\longrightarrow} \mathfrak{t}_{G, \mu} \otimes_k (\mathfrak{m}^{m}_{\widetilde{R}}/\mathfrak{m}^{m+1}_{\widetilde{R}}) \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathfrak{t}_{G, \mu} \otimes_k &(\mathfrak{m}^{m}_{\widetilde{R}}/\mathfrak{m}^{m+1}_{\widetilde{R}}) \overset{\mathrm{Diff}^{-1}_{h}}{\longrightarrow} {\mathrm{Hom}}(R_{G, \mu}, \widetilde{R}_{m+1})_{g} \\ &\overset{{\mathrm{ev}}_{\mathfrak{Q}}}{\longrightarrow} {\mathrm{Def}}(\mathfrak{Q}_g)_{(\mathfrak{S}_{\widetilde{{\mathcal O}}, m+1}, (\mathcal{E}))} \overset{{\mathrm{Per}}^{\beta}_{\mathfrak{Q}_h}}{\longrightarrow} \mathfrak{t}_{G, \mu} \otimes_k (\mathfrak{m}^{m}_{\widetilde{R}}/\mathfrak{m}^{m+1}_{\widetilde{R}}) \end{split} \end{align*} $$
 $\widetilde {k}$
-linear isomorphism. This composition is denoted by
$\widetilde {k}$
-linear isomorphism. This composition is denoted by
 $ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}. $
$ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}. $
Remark 4.3.8. Let the notation be as in Definition 4.3.7. The property (Perfd-lin) can be checked
![]() $\pi $
-completely flat locally on S. More precisely, let
$\pi $
-completely flat locally on S. More precisely, let
![]() $S \to S'$
be a
$S \to S'$
be a
![]() $\pi $
-completely faithfully flat homomorphism of perfectoid rings. Let
$\pi $
-completely faithfully flat homomorphism of perfectoid rings. Let
![]() $S"$
be the
$S"$
be the
![]() $\pi $
-adic completion of
$\pi $
-adic completion of
![]() $S' \otimes _S S'$
, which is a perfectoid ring (see [Reference Česnavičius and ScholzeČS24, Proposition 2.1.11]). If the condition in Definition 4.3.7 is satisfied for
$S' \otimes _S S'$
, which is a perfectoid ring (see [Reference Česnavičius and ScholzeČS24, Proposition 2.1.11]). If the condition in Definition 4.3.7 is satisfied for
![]() $(S', a^\flat )$
and
$(S', a^\flat )$
and
![]() $(S", a^\flat )$
(cf. Lemma 2.2.3 (1)), then it is also satisfied for
$(S", a^\flat )$
(cf. Lemma 2.2.3 (1)), then it is also satisfied for
![]() $(S, a^\flat )$
. Indeed, since
$(S, a^\flat )$
. Indeed, since
![]() $\pi =0$
in
$\pi =0$
in
![]() $S/a$
, we see that
$S/a$
, we see that
![]() $S/a \to S'/a$
is faithfully flat and
$S/a \to S'/a$
is faithfully flat and
![]() $S"/a = S'/a \otimes _{S/a} S'/a$
. Therefore, the sequence
$S"/a = S'/a \otimes _{S/a} S'/a$
. Therefore, the sequence
is exact by flat descent, from which our claim follows. (The same holds if we replace
![]() $S"$
by a perfectoid ring which is
$S"$
by a perfectoid ring which is
![]() $\pi $
-completely faithfully flat over the
$\pi $
-completely faithfully flat over the
![]() $\pi $
-adic completion of
$\pi $
-adic completion of
![]() $S' \otimes _S S'$
.)
$S' \otimes _S S'$
.)
Lemma 4.3.9. Let
![]() $ \mathfrak {Q} $
be a prismatic G-
$ \mathfrak {Q} $
be a prismatic G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $R_{G, \mu }$
.
$R_{G, \mu }$
.
-
(1) Assume that
 $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property  . Then
. Then
 $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
 $\mathrm {(Perfd)}$
.
$\mathrm {(Perfd)}$
. -
(2) Assume that
 $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property  . Then
. Then
 $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property
 $\mathrm {(BK)}$
.
$\mathrm {(BK)}$
.
Proof. (1) Let
![]() $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
![]() ${\mathcal O}$
. We want to prove that the map
${\mathcal O}$
. We want to prove that the map
is bijective for any
![]() $m \geq 1$
. It suffices to prove that for any
$m \geq 1$
. It suffices to prove that for any
![]() $m \geq 1$
and any
$m \geq 1$
and any
![]() $g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
, the map
$g \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m})_{e}$
, the map
is bijective. By Corollary 3.2.9, we may assume that
![]() $\mathfrak {Q}_e$
is banal. Then the assertion follows from the property
$\mathfrak {Q}_e$
is banal. Then the assertion follows from the property ![]() and Theorem 3.3.4.
and Theorem 3.3.4.
(2) This follows by the same argument as in (1).
The following proposition is the main reason for introducing (Perfd-lin) and (BK-lin).
Proposition 4.3.10. Let
![]() $ \mathfrak {Q} $
be a prismatic G-
$ \mathfrak {Q} $
be a prismatic G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $R_{G, \mu }$
. Assume that
$R_{G, \mu }$
. Assume that
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property ![]() . Then
. Then
![]() $\mathfrak {Q}$
has the property
$\mathfrak {Q}$
has the property ![]() .
.
Proof. With the notation of Definition 4.3.7, we want to prove that for any homomorphism
![]() $h \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_{m+1})_{g}$
and any isomorphism
$h \in {\mathrm {Hom}} (R_{G, \mu }, \widetilde {R}_{m+1})_{g}$
and any isomorphism
![]() $\beta \colon \mathfrak {Q}_g \overset {\sim }{\to } \mathcal {Q}_X$
, the map
$\beta \colon \mathfrak {Q}_g \overset {\sim }{\to } \mathcal {Q}_X$
, the map
is a
![]() $\widetilde {k}$
-linear isomorphism. We first prove that
$\widetilde {k}$
-linear isomorphism. We first prove that
![]() $\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is a
$\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is a
![]() $\widetilde {k}$
-linear homomorphism. For two elements
$\widetilde {k}$
-linear homomorphism. For two elements
![]() $g_1, g_2 \in \mathfrak {t}_{G, \mu } \otimes _k (\mathfrak {m}^{m}_{\widetilde {R}}/\mathfrak {m}^{m+1}_{\widetilde {R}})$
, we claim that
$g_1, g_2 \in \mathfrak {t}_{G, \mu } \otimes _k (\mathfrak {m}^{m}_{\widetilde {R}}/\mathfrak {m}^{m+1}_{\widetilde {R}})$
, we claim that
Indeed, by virtue of Corollary 4.2.6, it suffices to prove that for any perfectoid pair
![]() $(V, a^\flat )$
over
$(V, a^\flat )$
over
![]() $\widetilde {{\mathcal O}}$
and any map
$\widetilde {{\mathcal O}}$
and any map
![]() $ f \colon (\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(V^\flat )/[a^\flat ]^{m+1}, I_V) $
over
$ f \colon (\mathfrak {S}_{\widetilde {{\mathcal O}}}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(V^\flat )/[a^\flat ]^{m+1}, I_V) $
over
![]() $\widetilde {{\mathcal O}}$
, the induced homomorphism
$\widetilde {{\mathcal O}}$
, the induced homomorphism
sends the element
![]() $ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g_1+g_2)-\mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g_1)-\mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g_2) $
to
$ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g_1+g_2)-\mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g_1)-\mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g_2) $
to
![]() $0$
. Let
$0$
. Let
![]() $h' \colon R_{G, \mu } \to V/a^{m+1}$
be the composition of h with the induced homomorphism
$h' \colon R_{G, \mu } \to V/a^{m+1}$
be the composition of h with the induced homomorphism
![]() $\widetilde {R}_{m+1} \to V/a^{m+1}$
, and let
$\widetilde {R}_{m+1} \to V/a^{m+1}$
, and let
![]() $\beta '$
be the base change of
$\beta '$
be the base change of
![]() $\beta $
along the map
$\beta $
along the map
![]() $ (\mathfrak {S}_{\widetilde {{\mathcal O}}, m}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(V^\flat )/[a^\flat ]^{m}, I_V) $
induced from f. The following diagram is commutative:
$ (\mathfrak {S}_{\widetilde {{\mathcal O}}, m}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(V^\flat )/[a^\flat ]^{m}, I_V) $
induced from f. The following diagram is commutative:

Since
![]() $\mathrm {L}^{\beta '}_{\mathfrak {Q}, h'}$
is a
$\mathrm {L}^{\beta '}_{\mathfrak {Q}, h'}$
is a
![]() $V/a$
-linear homomorphism by our assumption, the claim follows. We can prove that
$V/a$
-linear homomorphism by our assumption, the claim follows. We can prove that
![]() $ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}(bg)=b\mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g) $
for any
$ \mathrm {L}^{\beta }_{\mathfrak {Q}, h}(bg)=b\mathrm {L}^{\beta }_{\mathfrak {Q}, h}(g) $
for any
![]() $b \in \widetilde {k}$
and any
$b \in \widetilde {k}$
and any
![]() $g \in \mathfrak {t}_{G, \mu } \otimes _k (\mathfrak {m}^{m}_R/\mathfrak {m}^{m+1}_R)$
in the same way. Thus, we conclude that
$g \in \mathfrak {t}_{G, \mu } \otimes _k (\mathfrak {m}^{m}_R/\mathfrak {m}^{m+1}_R)$
in the same way. Thus, we conclude that
![]() $\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is a
$\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is a
![]() $\widetilde {k}$
-linear homomorphism.
$\widetilde {k}$
-linear homomorphism.
It remains to prove that
![]() $\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is bijective. Since we have shown that
$\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is bijective. Since we have shown that
![]() $\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is a
$\mathrm {L}^{\beta }_{\mathfrak {Q}, h}$
is a
![]() $\widetilde {k}$
-linear endomorphism of the finite dimensional
$\widetilde {k}$
-linear endomorphism of the finite dimensional
![]() $\widetilde {k}$
-vector space
$\widetilde {k}$
-vector space
![]() $\mathfrak {t}_{G, \mu } \otimes _k (\mathfrak {m}^{m}_{\widetilde {R}}/\mathfrak {m}^{m+1}_{\widetilde {R}})$
, it suffices to prove that its kernel is zero. This follows from the same argument as above (since
$\mathfrak {t}_{G, \mu } \otimes _k (\mathfrak {m}^{m}_{\widetilde {R}}/\mathfrak {m}^{m+1}_{\widetilde {R}})$
, it suffices to prove that its kernel is zero. This follows from the same argument as above (since
![]() $\mathrm {L}^{\beta '}_{\mathfrak {Q}, h'}$
is injective by our assumption).
$\mathrm {L}^{\beta '}_{\mathfrak {Q}, h'}$
is injective by our assumption).
Remark 4.3.11. Let
![]() $\mathfrak {Q}$
be a deformation of
$\mathfrak {Q}$
be a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
. In summary, we have the following implications for
$R_{G, \mu }$
. In summary, we have the following implications for
![]() $\mathfrak {Q}$
:
$\mathfrak {Q}$
:

We will prove in Section 4.4 below that there exists a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
with the property
$R_{G, \mu }$
with the property ![]() . This in turn implies that all these conditions are equivalent for deformations of
. This in turn implies that all these conditions are equivalent for deformations of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
.
$R_{G, \mu }$
.
4.4 Constructions of universal deformations
Since
![]() $\mu $
is 1-bounded, there is an isomorphism
$\mu $
is 1-bounded, there is an isomorphism
of group schemes over
![]() ${\mathcal O}$
; see [Reference ItoIto23, Lemma 4.2.6]. We fix such an isomorphism. This induces an identification
${\mathcal O}$
; see [Reference ItoIto23, Lemma 4.2.6]. We fix such an isomorphism. This induces an identification
![]() $ R_{G, \mu } \simeq {\mathcal O}[[t_1, \dotsc , t_r]] $
over
$ R_{G, \mu } \simeq {\mathcal O}[[t_1, \dotsc , t_r]] $
over
![]() ${\mathcal O}$
. We set
${\mathcal O}$
. We set
so that
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
is an
$(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
is an
![]() ${\mathcal O}_E$
-prism of Breuil–Kisin type over
${\mathcal O}_E$
-prism of Breuil–Kisin type over
![]() ${\mathcal O}$
. We obtain the following isomorphism defined by
${\mathcal O}$
. We obtain the following isomorphism defined by
![]() $t_{r+1} \mapsto \pi $
:
$t_{r+1} \mapsto \pi $
:
For a G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $({\mathcal O}, (\pi ))$
, we will construct a deformation of
$({\mathcal O}, (\pi ))$
, we will construct a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
such that the corresponding deformation over
$(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
such that the corresponding deformation over
![]() $R_{G, \mu }$
has the property
$R_{G, \mu }$
has the property ![]() .
.
We need a lemma which allows us to reduce the problem to the case where
![]() $\mathcal {Q}$
is banal. Let
$\mathcal {Q}$
is banal. Let
![]() $\widetilde {k}$
be a finite Galois extension of k, and we set
$\widetilde {k}$
be a finite Galois extension of k, and we set
![]() $\widetilde {{\mathcal O}}:=W(\widetilde {k}) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E$
. Let
$\widetilde {{\mathcal O}}:=W(\widetilde {k}) \otimes _{W({\mathbb F}_q)} {\mathcal O}_E$
. Let
![]() $\widetilde {\mu } \colon {\mathbb G}_m \to G_{\widetilde {{\mathcal O}}}$
be the base change of
$\widetilde {\mu } \colon {\mathbb G}_m \to G_{\widetilde {{\mathcal O}}}$
be the base change of
![]() $\mu $
. We define
$\mu $
. We define
![]() $R_{G, \widetilde {\mu }} \in \mathcal {C}_{\widetilde {{\mathcal O}}}$
in the same way as
$R_{G, \widetilde {\mu }} \in \mathcal {C}_{\widetilde {{\mathcal O}}}$
in the same way as
![]() $R_{G, \mu }$
; see Definition 3.4.3. We have
$R_{G, \mu }$
; see Definition 3.4.3. We have
![]() $ R_{G, \mu }\otimes _{\mathcal O} \widetilde {{\mathcal O}} \overset {\sim }{\to } R_{G, \widetilde {\mu }}. $
$ R_{G, \mu }\otimes _{\mathcal O} \widetilde {{\mathcal O}} \overset {\sim }{\to } R_{G, \widetilde {\mu }}. $
Lemma 4.4.1. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. Assume that the base change
$({\mathcal O}, (\pi ))$
. Assume that the base change
![]() $\widetilde {\mathcal {Q}}$
of
$\widetilde {\mathcal {Q}}$
of
![]() $\mathcal {Q}$
to
$\mathcal {Q}$
to
![]() $(\widetilde {{\mathcal O}}, (\pi ))$
is banal. If there exists a deformation
$(\widetilde {{\mathcal O}}, (\pi ))$
is banal. If there exists a deformation
![]() $\widetilde {\mathfrak {Q}}$
of
$\widetilde {\mathfrak {Q}}$
of
![]() $\widetilde {\mathcal {Q}}$
over
$\widetilde {\mathcal {Q}}$
over
![]() $R_{G, \widetilde {\mu }}$
having the property
$R_{G, \widetilde {\mu }}$
having the property ![]() , then the same holds for
, then the same holds for
![]() $\mathcal {Q}$
(i.e., there exists a deformation of
$\mathcal {Q}$
(i.e., there exists a deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
having the property
$R_{G, \mu }$
having the property ![]() ).
).
Proof. The proof is divided into four parts.
Step 1. Let
![]() $ {\mathrm {Gal}} (\widetilde {k}/k)$
be the Galois group of
$ {\mathrm {Gal}} (\widetilde {k}/k)$
be the Galois group of
![]() $\widetilde {k}$
over k. For an
$\widetilde {k}$
over k. For an
![]() ${\mathcal O}$
-algebra A, each
${\mathcal O}$
-algebra A, each
![]() $s \in {\mathrm {Gal}} (\widetilde {k}/k)$
induces an automorphism of
$s \in {\mathrm {Gal}} (\widetilde {k}/k)$
induces an automorphism of
![]() $A \otimes _{{\mathcal O}} \widetilde {{\mathcal O}}$
over
$A \otimes _{{\mathcal O}} \widetilde {{\mathcal O}}$
over
![]() ${\mathcal O}$
, which we denote by the same symbol s. In particular, since
${\mathcal O}$
, which we denote by the same symbol s. In particular, since
![]() $R_{G, \widetilde {\mu }}=R_{G, \mu }\otimes _{\mathcal O} \widetilde {{\mathcal O}}$
, we have an automorphism
$R_{G, \widetilde {\mu }}=R_{G, \mu }\otimes _{\mathcal O} \widetilde {{\mathcal O}}$
, we have an automorphism
![]() $ s \colon R_{G, \widetilde {\mu }} \overset {\sim }{\to } R_{G, \widetilde {\mu }} $
over
$ s \colon R_{G, \widetilde {\mu }} \overset {\sim }{\to } R_{G, \widetilde {\mu }} $
over
![]() ${\mathcal O}$
. Since
${\mathcal O}$
. Since
![]() $s^*(\widetilde {\mathcal {Q}})=\widetilde {\mathcal {Q}}$
, the base change
$s^*(\widetilde {\mathcal {Q}})=\widetilde {\mathcal {Q}}$
, the base change
![]() $s^*(\widetilde {\mathfrak {Q}})$
is a deformation of
$s^*(\widetilde {\mathfrak {Q}})$
is a deformation of
![]() $\widetilde {\mathcal {Q}}$
over
$\widetilde {\mathcal {Q}}$
over
![]() $R_{G, \widetilde {\mu }}$
. By Remark 4.3.11, we see that
$R_{G, \widetilde {\mu }}$
. By Remark 4.3.11, we see that
![]() $\widetilde {\mathfrak {Q}}$
, and hence,
$\widetilde {\mathfrak {Q}}$
, and hence,
![]() $s^*(\widetilde {\mathfrak {Q}})$
is a universal deformation of
$s^*(\widetilde {\mathfrak {Q}})$
is a universal deformation of
![]() $\widetilde {\mathcal {Q}}$
. Thus, there exists a unique isomorphism
$\widetilde {\mathcal {Q}}$
. Thus, there exists a unique isomorphism
![]() $ h_s \colon R_{G, \widetilde {\mu }} \overset {\sim }{\to } R_{G, \widetilde {\mu }} $
over
$ h_s \colon R_{G, \widetilde {\mu }} \overset {\sim }{\to } R_{G, \widetilde {\mu }} $
over
![]() $\widetilde {{\mathcal O}}$
such that
$\widetilde {{\mathcal O}}$
such that
![]() $ h^*_s(\widetilde {\mathfrak {Q}}) \simeq s^*(\widetilde {\mathfrak {Q}}) $
as deformations of
$ h^*_s(\widetilde {\mathfrak {Q}}) \simeq s^*(\widetilde {\mathfrak {Q}}) $
as deformations of
![]() $\widetilde {\mathcal {Q}}$
. We have
$\widetilde {\mathcal {Q}}$
. We have
for all
![]() $s, s' \in {\mathrm {Gal}} (\widetilde {k}/k)$
. Here,
$s, s' \in {\mathrm {Gal}} (\widetilde {k}/k)$
. Here,
![]() $s(h_{s'}) \colon R_{G, \widetilde {\mu }} \to R_{G, \widetilde {\mu }}$
is the base change of
$s(h_{s'}) \colon R_{G, \widetilde {\mu }} \to R_{G, \widetilde {\mu }}$
is the base change of
![]() $h_{s'}$
along s.
$h_{s'}$
along s.
Step 2. Since
the automorphisms
![]() $h_s$
induce automorphisms
$h_s$
induce automorphisms
over
![]() $\widetilde {k}$
satisfying the same relation as (4.1). The set of automorphisms of
$\widetilde {k}$
satisfying the same relation as (4.1). The set of automorphisms of
![]() $\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
over
$\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
over
![]() $\widetilde {k}$
can be identified with
$\widetilde {k}$
can be identified with
![]() $ {\mathrm {GL}} _r(\widetilde {k})$
. Since the Galois cohomology
$ {\mathrm {GL}} _r(\widetilde {k})$
. Since the Galois cohomology
![]() $H^1( {\mathrm {Gal}} (\widetilde {k}/k), {\mathrm {GL}} _r(\widetilde {k}))$
has only one element, there exists an automorphism
$H^1( {\mathrm {Gal}} (\widetilde {k}/k), {\mathrm {GL}} _r(\widetilde {k}))$
has only one element, there exists an automorphism
![]() $g'$
of
$g'$
of
![]() $\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
over
$\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
over
![]() $\widetilde {k}$
such that
$\widetilde {k}$
such that
![]() $h^{\prime }_s=s(g^{\prime -1}) \circ g'$
for any
$h^{\prime }_s=s(g^{\prime -1}) \circ g'$
for any
![]() $s \in {\mathrm {Gal}} (\widetilde {k}/k)$
. Let g be an automorphism of
$s \in {\mathrm {Gal}} (\widetilde {k}/k)$
. Let g be an automorphism of
![]() $R_{G, \widetilde {\mu }}$
over
$R_{G, \widetilde {\mu }}$
over
![]() $\widetilde {{\mathcal O}}$
lifting
$\widetilde {{\mathcal O}}$
lifting
![]() $g'$
. By replacing
$g'$
. By replacing
![]() $\widetilde {\mathfrak {Q}}$
by
$\widetilde {\mathfrak {Q}}$
by
![]() $g^*(\widetilde {\mathfrak {Q}})$
, we may assume that the automorphisms
$g^*(\widetilde {\mathfrak {Q}})$
, we may assume that the automorphisms
![]() $h_s$
induce the identity on
$h_s$
induce the identity on
![]() $\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
.
$\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
.
Step 3. The
![]() ${\mathcal O}_E$
-prism
${\mathcal O}_E$
-prism
![]() $ (\widetilde {{\mathcal O}}[[t_1, \dotsc , t_r]]/(t_1, \dotsc , t_r)^2, (\pi )) $
is naturally an object of the category
$ (\widetilde {{\mathcal O}}[[t_1, \dotsc , t_r]]/(t_1, \dotsc , t_r)^2, (\pi )) $
is naturally an object of the category ![]() . Since
. Since
![]() $h_s$
is a lift of the identity of
$h_s$
is a lift of the identity of
![]() $\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
, we have
$\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
, we have
see also Remark 2.6.2. However, we have
Thus, the isomorphism
![]() $h^*_s(\widetilde {\mathfrak {Q}}) \simeq s^*(\widetilde {\mathfrak {Q}})$
induces an isomorphism
$h^*_s(\widetilde {\mathfrak {Q}}) \simeq s^*(\widetilde {\mathfrak {Q}})$
induces an isomorphism
of deformations of
![]() $\widetilde {\mathcal {Q}}$
. Then, by Galois descent (see Corollary 3.2.9), we see that
$\widetilde {\mathcal {Q}}$
. Then, by Galois descent (see Corollary 3.2.9), we see that
arises from a deformation
![]() $\mathscr {Q}'$
of
$\mathscr {Q}'$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $({\mathcal O}[[t_1, \dotsc , t_r]]/(t_1, \dotsc , t_r)^2, (\pi ))$
.
$({\mathcal O}[[t_1, \dotsc , t_r]]/(t_1, \dotsc , t_r)^2, (\pi ))$
.
The homomorphism
![]() $\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O} \to {\mathcal O}[[t_1, \dotsc , t_r]]/(t_1, \dotsc , t_r)^2$
, defined by
$\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O} \to {\mathcal O}[[t_1, \dotsc , t_r]]/(t_1, \dotsc , t_r)^2$
, defined by
![]() $t_i \mapsto t_i$
(
$t_i \mapsto t_i$
(
![]() $1 \leq i \leq r$
) and
$1 \leq i \leq r$
) and
![]() $t_{r+1} \mapsto 0$
, induces a morphism
$t_{r+1} \mapsto 0$
, induces a morphism
in ![]() . By Proposition 3.1.5 and Proposition 3.4.6, there exists a deformation
. By Proposition 3.1.5 and Proposition 3.4.6, there exists a deformation
![]() $\mathscr {Q}$
of
$\mathscr {Q}$
of
![]() $\mathscr {Q}'$
over
$\mathscr {Q}'$
over
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
.
$(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
.
Step 4. The deformation
![]() $\mathfrak {Q}$
of
$\mathfrak {Q}$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
corresponding to
$R_{G, \mu }$
corresponding to
![]() $\mathscr {Q}$
has the property
$\mathscr {Q}$
has the property ![]() . Indeed, let
. Indeed, let
![]() $\iota \colon R_{G, \mu } \to R_{G, \widetilde {\mu }}$
be the inclusion. It is enough to show that
$\iota \colon R_{G, \mu } \to R_{G, \widetilde {\mu }}$
be the inclusion. It is enough to show that
![]() $\iota ^*\mathfrak {Q}$
has the property
$\iota ^*\mathfrak {Q}$
has the property ![]() . (To check that the condition in Definition 4.3.7 is satisfied for a perfectoid pair
. (To check that the condition in Definition 4.3.7 is satisfied for a perfectoid pair
![]() $(S, a^\flat )$
over
$(S, a^\flat )$
over
![]() ${\mathcal O}$
, it suffices to check it for the induced perfectoid pair
${\mathcal O}$
, it suffices to check it for the induced perfectoid pair
![]() $(S \otimes _{{\mathcal O}} \widetilde {{\mathcal O}}, a^\flat )$
; see Remark 4.3.8.) Let
$(S \otimes _{{\mathcal O}} \widetilde {{\mathcal O}}, a^\flat )$
; see Remark 4.3.8.) Let
![]() $h \colon R_{G, \widetilde {\mu }} \to R_{G, \widetilde {\mu }}$
be the unique local homomorphism over
$h \colon R_{G, \widetilde {\mu }} \to R_{G, \widetilde {\mu }}$
be the unique local homomorphism over
![]() $\widetilde {{\mathcal O}}$
such that
$\widetilde {{\mathcal O}}$
such that
![]() $h^*(\widetilde {\mathfrak {Q}}) \simeq \iota ^*\mathfrak {Q}$
as deformations of
$h^*(\widetilde {\mathfrak {Q}}) \simeq \iota ^*\mathfrak {Q}$
as deformations of
![]() $\widetilde {\mathcal {Q}}$
. By construction, we have
$\widetilde {\mathcal {Q}}$
. By construction, we have
Since
![]() $\widetilde {\mathfrak {Q}}$
has the property
$\widetilde {\mathfrak {Q}}$
has the property ![]() by Proposition 4.3.10, it follows that h induces the identity on
by Proposition 4.3.10, it follows that h induces the identity on
![]() $\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
. In particular, h is an isomorphism, which in turn implies that
$\widetilde {k}[t_1, \dotsc , t_r]/(t_1, \dotsc , t_r)^2$
. In particular, h is an isomorphism, which in turn implies that
![]() $\iota ^*\mathfrak {Q}$
has the property
$\iota ^*\mathfrak {Q}$
has the property ![]() . This concludes the proof.
. This concludes the proof.
Theorem 4.4.2. Let
![]() $\mathcal {Q}$
be a G-
$\mathcal {Q}$
be a G-
![]() $\mu $
-display over
$\mu $
-display over
![]() $({\mathcal O}, (\pi ))$
. There exists a deformation
$({\mathcal O}, (\pi ))$
. There exists a deformation
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
of
$\mathfrak {Q}^{ {\mathrm {univ}} }$
of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
having the property
$R_{G, \mu }$
having the property ![]() . In particular,
. In particular,
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
is a universal deformation of
$\mathfrak {Q}^{ {\mathrm {univ}} }$
is a universal deformation of
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Proof. By Lemma 4.4.1, we may assume that
![]() $\mathcal {Q}=\mathcal {Q}_X$
for some
$\mathcal {Q}=\mathcal {Q}_X$
for some
![]() $X \in G({\mathcal O})_{(\pi )}$
. Let
$X \in G({\mathcal O})_{(\pi )}$
. Let
![]() $ U \in G(R_{G, \mu }) $
be the
$ U \in G(R_{G, \mu }) $
be the
![]() $R_{G, \mu }$
-valued point corresponding to the composition
$R_{G, \mu }$
-valued point corresponding to the composition
![]() $ \mathrm {Spec} R_{G, \mu } \to U^{-}_{\mu } \to G_{\mathcal O}. $
We define
$ \mathrm {Spec} R_{G, \mu } \to U^{-}_{\mu } \to G_{\mathcal O}. $
We define
as the image of
![]() $U \in G(R_{G, \mu })$
under the homomorphism
$U \in G(R_{G, \mu })$
under the homomorphism
![]() $G(R_{G, \mu }) \to G(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O})$
induced by
$G(R_{G, \mu }) \to G(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O})$
induced by
![]() $t_i \mapsto t_i$
(
$t_i \mapsto t_i$
(
![]() $1 \leq i \leq r$
). Let
$1 \leq i \leq r$
). Let
![]() $X^{ {\mathrm {univ}} } \in G(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O})_{(\mathcal {E})}$
be the element such that
$X^{ {\mathrm {univ}} } \in G(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O})_{(\mathcal {E})}$
be the element such that
(Here, the image of
![]() $X_\pi \in G({\mathcal O})$
in
$X_\pi \in G({\mathcal O})$
in
![]() $G(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O})$
is denoted by the same symbol. See also (2.1) for
$G(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O})$
is denoted by the same symbol. See also (2.1) for
![]() $(X^{ {\mathrm {univ}} })_{\mathcal {E}}$
and
$(X^{ {\mathrm {univ}} })_{\mathcal {E}}$
and
![]() $X_\pi $
.) Then the G-
$X_\pi $
.) Then the G-
![]() $\mu $
-display
$\mu $
-display
![]() $\mathcal {Q}_{X^{ {\mathrm {univ}} }}$
over
$\mathcal {Q}_{X^{ {\mathrm {univ}} }}$
over
![]() $(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
is naturally a deformation of
$(\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E}))$
is naturally a deformation of
![]() $\mathcal {Q}_X$
. Let
$\mathcal {Q}_X$
. Let
![]() $ \mathfrak {Q}^{ {\mathrm {univ}} } $
be the deformation of
$ \mathfrak {Q}^{ {\mathrm {univ}} } $
be the deformation of
![]() $\mathcal {Q}_X$
over
$\mathcal {Q}_X$
over
![]() $R_{G, \mu }$
such that
$R_{G, \mu }$
such that
We shall prove that
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
has the property
$\mathfrak {Q}^{ {\mathrm {univ}} }$
has the property ![]() . In other words, with the notation of Definition 4.3.7, we want to show that for any
. In other words, with the notation of Definition 4.3.7, we want to show that for any
![]() $\widetilde {g} \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
and any isomorphism
$\widetilde {g} \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
and any isomorphism
![]() $\beta \colon \mathfrak {Q}^{ {\mathrm {univ}} }_g \overset {\sim }{\to } \mathcal {Q}_Y$
, the map
$\beta \colon \mathfrak {Q}^{ {\mathrm {univ}} }_g \overset {\sim }{\to } \mathcal {Q}_Y$
, the map
is an
![]() $S/a$
-linear isomorphism. By Remark 4.2.3 and Remark 4.3.8, we are reduced to the case where the map
$S/a$
-linear isomorphism. By Remark 4.2.3 and Remark 4.3.8, we are reduced to the case where the map
![]() $S \to S$
,
$S \to S$
,
![]() $x \mapsto x^p$
is surjective. By Lemma 4.2.2, the homomorphism
$x \mapsto x^p$
is surjective. By Lemma 4.2.2, the homomorphism
![]() $\widetilde {g}$
then lifts to a primitive map
$\widetilde {g}$
then lifts to a primitive map
Let
![]() $f \colon (\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m}, I_S)$
be the map induced by
$f \colon (\mathfrak {S}^{ {\mathrm {univ}} }_{\mathcal O}, (\mathcal {E})) \to (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m}, I_S)$
be the map induced by
![]() $\widetilde {f}$
. Without loss of generality, we may assume that
$\widetilde {f}$
. Without loss of generality, we may assume that
![]() $Y=f(X^{ {\mathrm {univ}} })$
in
$Y=f(X^{ {\mathrm {univ}} })$
in
![]() $G(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m})_{I_S}$
and
$G(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m})_{I_S}$
and
![]() $\beta $
is the following composition:
$\beta $
is the following composition:
see the last paragraph of Remark 3.4.8. In this case, we claim that
![]() $\mathrm {L}^{\beta }_{\mathfrak {Q}^{ {\mathrm {univ}} }, \widetilde {g}}$
is the identity map. Let
$\mathrm {L}^{\beta }_{\mathfrak {Q}^{ {\mathrm {univ}} }, \widetilde {g}}$
is the identity map. Let
![]() $g' \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
. By Lemma 4.2.4, there exists a map
$g' \in {\mathrm {Hom}} (R_{G, \mu }, S/a^{m+1})_{g}$
. By Lemma 4.2.4, there exists a map
of
![]() ${\mathcal O}_E$
-prisms which induces
${\mathcal O}_E$
-prisms which induces
![]() $g'$
and f. It suffices to show that the period map
$g'$
and f. It suffices to show that the period map
sends the deformation
![]() $\mathcal {Q}_{f'(X^{ {\mathrm {univ}} })}$
to
$\mathcal {Q}_{f'(X^{ {\mathrm {univ}} })}$
to
![]() $\mathrm {Diff}_{\widetilde {g}}(g')$
. Here, as in Remark 3.4.8, we identify
$\mathrm {Diff}_{\widetilde {g}}(g')$
. Here, as in Remark 3.4.8, we identify
with
![]() $\mathfrak {t}_{G, \mu } \otimes _k (a^{m}S/a^{m+1}S)$
. We set
$\mathfrak {t}_{G, \mu } \otimes _k (a^{m}S/a^{m+1}S)$
. We set
![]() $d:=\widetilde {f}(\mathcal {E})$
. We have
$d:=\widetilde {f}(\mathcal {E})$
. We have
![]() $f'(\mathcal {E})=u d$
for a unique
$f'(\mathcal {E})=u d$
for a unique
![]() $u \in (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1})^\times $
. Since the image of u in
$u \in (W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1})^\times $
. Since the image of u in
![]() $W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m}$
is equal to
$W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m}$
is equal to
![]() $1$
, the equality
$1$
, the equality
![]() $\phi (\mu (u))=1$
holds in
$\phi (\mu (u))=1$
holds in
![]() $G(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1})$
. Then we have
$G(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1})$
. Then we have
in
![]() $G(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1})$
. By the proof of Proposition 3.2.7, the unique isomorphism
$G(W_{{\mathcal O}_E}(S^\flat )/[a^\flat ]^{m+1})$
. By the proof of Proposition 3.2.7, the unique isomorphism
of deformations of the underlying G-
![]() $\phi $
-module
$\phi $
-module
![]() $(\mathcal {Q}_{f(X^{ {\mathrm {univ}} })})_\phi $
is given by
$(\mathcal {Q}_{f(X^{ {\mathrm {univ}} })})_\phi $
is given by
![]() $\widetilde {f}(U^{ {\mathrm {univ}} })^{-1}f'(U^{ {\mathrm {univ}} })$
. Thus, the lift
$\widetilde {f}(U^{ {\mathrm {univ}} })^{-1}f'(U^{ {\mathrm {univ}} })$
. Thus, the lift
![]() $ {\mathrm {Per}} _{\mathcal {Q}_{\widetilde {f}(X^{ {\mathrm {univ}} })}}(\mathcal {Q}_{f'(X^{ {\mathrm {univ}} })})$
of the Hodge filtration can be identified with the
$ {\mathrm {Per}} _{\mathcal {Q}_{\widetilde {f}(X^{ {\mathrm {univ}} })}}(\mathcal {Q}_{f'(X^{ {\mathrm {univ}} })})$
of the Hodge filtration can be identified with the
![]() $P_\mu (S/a^{m+1})$
-orbit
$P_\mu (S/a^{m+1})$
-orbit
and this corresponds to
![]() $\mathrm {Diff}_{\widetilde {g}}(g') \in \mathfrak {t}_{G, \mu } \otimes _k (a^{m}S/a^{m+1}S)$
as desired. This concludes the proof of Theorem 4.4.2.
$\mathrm {Diff}_{\widetilde {g}}(g') \in \mathfrak {t}_{G, \mu } \otimes _k (a^{m}S/a^{m+1}S)$
as desired. This concludes the proof of Theorem 4.4.2.
We can now complete the proofs of Theorem 4.1.7 and Theorem 4.1.8.
Proof of Theorem 4.1.8.
We have already proved that (1) implies (2), (3), (4) and (5); see Theorem 4.1.7. By Corollary 4.3.3, we have
![]() $(2) \Rightarrow (1)$
.
$(2) \Rightarrow (1)$
.
Let
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
be a universal deformation of
$\mathfrak {Q}^{ {\mathrm {univ}} }$
be a universal deformation of
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $R_{G, \mu }$
, which has the properties
$R_{G, \mu }$
, which has the properties
![]() $\mathrm {(Perfd)}$
and
$\mathrm {(Perfd)}$
and
![]() $\mathrm {(BK)}$
by Theorem 4.1.7. Let
$\mathrm {(BK)}$
by Theorem 4.1.7. Let
![]() $h \colon R_{G, \mu } \to R$
be the unique local homomorphism over
$h \colon R_{G, \mu } \to R$
be the unique local homomorphism over
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() $h^*(\mathfrak {Q}^{ {\mathrm {univ}} }) \simeq \mathfrak {Q}$
.
$h^*(\mathfrak {Q}^{ {\mathrm {univ}} }) \simeq \mathfrak {Q}$
.
We assume that (5) holds. By Remark 4.3.5, the induced homomorphism
![]() $\mathfrak {t}_R \to \mathfrak {t}_{G, \mu }$
is surjective. Since
$\mathfrak {t}_R \to \mathfrak {t}_{G, \mu }$
is surjective. Since
![]() $\dim _k \mathfrak {t}_R = \dim _k \mathfrak {t}_{G, \mu }$
, we then have
$\dim _k \mathfrak {t}_R = \dim _k \mathfrak {t}_{G, \mu }$
, we then have
![]() $\mathfrak {t}_R \overset {\sim }{\to } \mathfrak {t}_{G, \mu }$
. It follows that
$\mathfrak {t}_R \overset {\sim }{\to } \mathfrak {t}_{G, \mu }$
. It follows that
![]() $h \colon R_{G, \mu } \to R$
is surjective. Since
$h \colon R_{G, \mu } \to R$
is surjective. Since
![]() $\dim R=\dim R_{G, \mu }$
, we conclude that h is an isomorphism, and hence,
$\dim R=\dim R_{G, \mu }$
, we conclude that h is an isomorphism, and hence,
![]() $\mathfrak {Q}$
is a universal deformation. Thus, we have
$\mathfrak {Q}$
is a universal deformation. Thus, we have
![]() $(5) \Rightarrow (1)$
.
$(5) \Rightarrow (1)$
.
It is obvious that (3) implies (4). It remains to show that (4) implies (1). We assume that the evaluation map
is bijective, where the base change of
![]() $\mathcal {Q}$
to
$\mathcal {Q}$
to
![]() $(W_{{\mathcal O}_E}({\mathcal O}_{C^\flat })/[\pi ^\flat ], I_{{\mathcal O}_C})$
is denoted by the same symbol. Since
$(W_{{\mathcal O}_E}({\mathcal O}_{C^\flat })/[\pi ^\flat ], I_{{\mathcal O}_C})$
is denoted by the same symbol. Since
![]() $ {\mathrm {Def}} (\mathcal {Q})_{(W_{{\mathcal O}_E}({\mathcal O}_{C^\flat })/[\pi ^\flat ]^{2}, I_{{\mathcal O}_C})}$
is nonempty (by Remark 3.3.6 or Proposition 3.4.6), there exists a homomorphism
$ {\mathrm {Def}} (\mathcal {Q})_{(W_{{\mathcal O}_E}({\mathcal O}_{C^\flat })/[\pi ^\flat ]^{2}, I_{{\mathcal O}_C})}$
is nonempty (by Remark 3.3.6 or Proposition 3.4.6), there exists a homomorphism
![]() $g \colon R \to {\mathcal O}_C/\pi ^{2}$
which is a lift of e. In particular, it follows that
$g \colon R \to {\mathcal O}_C/\pi ^{2}$
which is a lift of e. In particular, it follows that
![]() $\pi $
is not contained in
$\pi $
is not contained in
![]() $\mathfrak {m}^2_R \subset R$
. The following diagram commutes:
$\mathfrak {m}^2_R \subset R$
. The following diagram commutes:

where the vertical arrows are induced from h. It follows that
and hence,
![]() $\mathfrak {t}_R \to \mathfrak {t}_{G, \mu }$
, is an isomorphism. This implies that
$\mathfrak {t}_R \to \mathfrak {t}_{G, \mu }$
, is an isomorphism. This implies that
![]() $h \colon R_{G, \mu } \to R$
is surjective. Since
$h \colon R_{G, \mu } \to R$
is surjective. Since
![]() $\pi $
is not contained in
$\pi $
is not contained in
![]() $\mathfrak {m}^2_R$
, we see that
$\mathfrak {m}^2_R$
, we see that
![]() $R/\pi $
is regular, or equivalently,
$R/\pi $
is regular, or equivalently,
![]() $\dim R/\pi = \dim _k \mathfrak {t}_R$
. We then obtain
$\dim R/\pi = \dim _k \mathfrak {t}_R$
. We then obtain
It follows that
![]() $h \colon R_{G, \mu } \to R$
is an isomorphism.
$h \colon R_{G, \mu } \to R$
is an isomorphism.
The proof of Theorem 4.1.8 is now complete.
5 Integral local Shimura varieties with hyperspecial level structure
In this section, as an application of our deformation theory, we prove the local representability and the formal smoothness of integral local Shimura varieties with hyperspecial level structure; see Theorem 5.3.5 for the precise statement. Throughout this section, we assume that G is a connected reductive group scheme over
![]() $ \mathrm {Spec} {\mathcal O}_E$
. We assume that k is an algebraic closure of
$ \mathrm {Spec} {\mathcal O}_E$
. We assume that k is an algebraic closure of
![]() ${\mathbb F}_q$
.
${\mathbb F}_q$
.
In Section 5.1, we recall the definition of G-shtukas (with one leg) over perfectoid spaces over k introduced by Scholze, and we discuss their relation to G-
![]() $\mu $
-displays. In Section 5.2, we study the notion of quasi-isogeny for G-shtukas. Integral local Shimura varieties are defined as moduli spaces of G-shtukas together with some quasi-isogeny. In Section 5.3, we prove the main result of this section.
$\mu $
-displays. In Section 5.2, we study the notion of quasi-isogeny for G-shtukas. Integral local Shimura varieties are defined as moduli spaces of G-shtukas together with some quasi-isogeny. In Section 5.3, we prove the main result of this section.
We assume that the reader is familiar with the theory of perfectoid spaces, v-sheaves, and ‘the curve’
![]() $\mathcal {Y}^{[0, \infty )}_S$
. Our basic references are [Reference ScholzeSch22], [Reference Scholze and WeinsteinSW20] and [Reference Fargues and ScholzeFS21].
$\mathcal {Y}^{[0, \infty )}_S$
. Our basic references are [Reference ScholzeSch22], [Reference Scholze and WeinsteinSW20] and [Reference Fargues and ScholzeFS21].
5.1 G-shtukas
Let
![]() $ {\mathrm {Perf}} _k $
be the category of perfectoid spaces over k. We endow
$ {\mathrm {Perf}} _k $
be the category of perfectoid spaces over k. We endow
![]() $ {\mathrm {Perf}} _k$
with the v-topology introduced in [Reference ScholzeSch22, Definition 8.1]. A sheaf on
$ {\mathrm {Perf}} _k$
with the v-topology introduced in [Reference ScholzeSch22, Definition 8.1]. A sheaf on
![]() $ {\mathrm {Perf}} _k$
with respect to the v-topology is called a v-sheaf.
$ {\mathrm {Perf}} _k$
with respect to the v-topology is called a v-sheaf.
Remark 5.1.1 (The notation in this section).
In this section, we let S stand for a perfectoid space over k (rather than a perfectoid ring). We write
Let
![]() $ {\mathrm {Spd}} {\mathcal O}_{\breve {E}} $
be the v-sheaf on
$ {\mathrm {Spd}} {\mathcal O}_{\breve {E}} $
be the v-sheaf on
![]() $ {\mathrm {Perf}} _k$
which sends a perfectoid space S over k to the set of isomorphism classes of untilts
$ {\mathrm {Perf}} _k$
which sends a perfectoid space S over k to the set of isomorphism classes of untilts
![]() $S^\sharp $
of S over
$S^\sharp $
of S over
![]() ${\mathcal O}_{\breve {E}}$
; see [Reference Scholze and WeinsteinSW20, Section 18.1]. If
${\mathcal O}_{\breve {E}}$
; see [Reference Scholze and WeinsteinSW20, Section 18.1]. If
![]() $S= \mathrm {Spa}(R, R^+)$
is an affinoid perfectoid space over k, then an untilt
$S= \mathrm {Spa}(R, R^+)$
is an affinoid perfectoid space over k, then an untilt
![]() $S^\sharp $
is also an affinoid perfectoid space, and we use the following notation:
$S^\sharp $
is also an affinoid perfectoid space, and we use the following notation:
The ring
![]() $R^{\sharp +}$
is a perfectoid ring (in the sense of [Reference Bhatt, Morrow and ScholzeBMS18]) with
$R^{\sharp +}$
is a perfectoid ring (in the sense of [Reference Bhatt, Morrow and ScholzeBMS18]) with
![]() $(R^{\sharp +})^\flat = R^+$
. Let
$(R^{\sharp +})^\flat = R^+$
. Let
![]() $\varpi ^\flat \in R^+$
be a pseudo-uniformizer (i.e., it is a topologically nilpotent unit in R). Then
$\varpi ^\flat \in R^+$
be a pseudo-uniformizer (i.e., it is a topologically nilpotent unit in R). Then
![]() $\varpi :=\theta ([\varpi ^\flat ]) \in R^{\sharp +}$
is also a pseudo-uniformizer. After replacing
$\varpi :=\theta ([\varpi ^\flat ]) \in R^{\sharp +}$
is also a pseudo-uniformizer. After replacing
![]() $\varpi ^\flat $
by
$\varpi ^\flat $
by
![]() $(\varpi ^\flat )^{1/p^n}$
for a large enough n, we may assume that
$(\varpi ^\flat )^{1/p^n}$
for a large enough n, we may assume that
![]() $\pi \in (\varpi )$
in
$\pi \in (\varpi )$
in
![]() $R^{\sharp +}$
. The pair
$R^{\sharp +}$
. The pair
![]() $(R^{\sharp +}, \varpi ^\flat )$
is a perfectoid pair in the sense of Definition 2.1.4.
$(R^{\sharp +}, \varpi ^\flat )$
is a perfectoid pair in the sense of Definition 2.1.4.
Example 5.1.2 (Product of points).
Let
![]() $\{ (C_i, C^{+}_i) \}_{i \in I}$
be a set of analytic affinoid fields over k such that
$\{ (C_i, C^{+}_i) \}_{i \in I}$
be a set of analytic affinoid fields over k such that
![]() $C_i$
is algebraically closed for any
$C_i$
is algebraically closed for any
![]() $i\in I$
. We choose a pseudo-uniformizer
$i\in I$
. We choose a pseudo-uniformizer
![]() $\varpi ^\flat _i \in C^{+}_i$
for each
$\varpi ^\flat _i \in C^{+}_i$
for each
![]() $i \in I$
. Let
$i \in I$
. Let
![]() $\varpi ^\flat := (\varpi ^\flat _i)_{i \in I} \in \prod _{i \in I} C^{+}_i$
. We endow
$\varpi ^\flat := (\varpi ^\flat _i)_{i \in I} \in \prod _{i \in I} C^{+}_i$
. We endow
![]() $\prod _{i \in I} C^{+}_i$
with the
$\prod _{i \in I} C^{+}_i$
with the
![]() $\varpi ^\flat $
-adic topology. Then
$\varpi ^\flat $
-adic topology. Then
is an affinoid perfectoid space over k. Following [Reference GleasonGle22b], we call such a perfectoid space a product of points. Products of points over k form a basis of
![]() $ {\mathrm {Perf}} _k$
with respect to the v-topology; see [Reference GleasonGle22b, Example 1.1]. Let
$ {\mathrm {Perf}} _k$
with respect to the v-topology; see [Reference GleasonGle22b, Example 1.1]. Let
![]() $S^\sharp $
be an untilt of S over
$S^\sharp $
be an untilt of S over
![]() ${\mathcal O}_{\breve {E}}$
. By [Reference ScholzeSch22, Corollary 3.20], we have the corresponding untilt
${\mathcal O}_{\breve {E}}$
. By [Reference ScholzeSch22, Corollary 3.20], we have the corresponding untilt
![]() $ \mathrm {Spa}(C^{\sharp }_i, C^{\sharp +}_i)$
of
$ \mathrm {Spa}(C^{\sharp }_i, C^{\sharp +}_i)$
of
![]() $ \mathrm {Spa}(C_i, C^{+}_i)$
over
$ \mathrm {Spa}(C_i, C^{+}_i)$
over
![]() $S^\sharp $
. Let
$S^\sharp $
. Let
![]() $\varpi _i:=\theta ([\varpi ^\flat _i]) \in C^{\sharp +}_i$
and let
$\varpi _i:=\theta ([\varpi ^\flat _i]) \in C^{\sharp +}_i$
and let
![]() $\varpi :=(\varpi _i)_{i \in I} \in \prod _{i \in I} C^{\sharp +}_i$
. Then the untilt
$\varpi :=(\varpi _i)_{i \in I} \in \prod _{i \in I} C^{\sharp +}_i$
. Then the untilt
![]() $S^\sharp $
is isomorphic to
$S^\sharp $
is isomorphic to
![]() $ \mathrm {Spa}((\prod _{i \in I} C^{\sharp +}_i)[1/\varpi ], \prod _{i \in I} C^{\sharp +}_i). $
$ \mathrm {Spa}((\prod _{i \in I} C^{\sharp +}_i)[1/\varpi ], \prod _{i \in I} C^{\sharp +}_i). $
We shall recall the definition of G-shtukas, following [Reference Scholze and WeinsteinSW20]. In the rest of this subsection, we assume that
![]() $S= \mathrm {Spa}(R, R^+)$
is an affinoid perfectoid space over k for simplicity. Let
$S= \mathrm {Spa}(R, R^+)$
is an affinoid perfectoid space over k for simplicity. Let
![]() $S^\sharp = \mathrm {Spa}(R^\sharp , R^{\sharp +})$
be an untilt of S over
$S^\sharp = \mathrm {Spa}(R^\sharp , R^{\sharp +})$
be an untilt of S over
![]() ${\mathcal O}_{\breve {E}}$
.
${\mathcal O}_{\breve {E}}$
.
We consider the following adic space:
where
![]() $\varpi ^\flat \in R^+$
is a pseudo-uniformizer and
$\varpi ^\flat \in R^+$
is a pseudo-uniformizer and
![]() $W_{{\mathcal O}_E}(R^+)$
is equipped with the
$W_{{\mathcal O}_E}(R^+)$
is equipped with the
![]() $(\pi , [\varpi ^\flat ])$
-adic topology. The adic space
$(\pi , [\varpi ^\flat ])$
-adic topology. The adic space
![]() $\mathcal {Y}^{[0, \infty )}_S$
is called the curve and denoted by
$\mathcal {Y}^{[0, \infty )}_S$
is called the curve and denoted by
![]() $\mathcal {Y}_S$
in [Reference Fargues and ScholzeFS21, Section II.1.1]. The curve
$\mathcal {Y}_S$
in [Reference Fargues and ScholzeFS21, Section II.1.1]. The curve
![]() $\mathcal {Y}^{[0, \infty )}_S$
is a sousperfectoid adic space over
$\mathcal {Y}^{[0, \infty )}_S$
is a sousperfectoid adic space over
![]() ${\mathcal O}_{\breve {E}}$
in the sense of [Reference Scholze and WeinsteinSW20, Definition 6.3.1, Appendix to Lecture 19]; see the proof of [Reference Fargues and ScholzeFS21, Proposition II.1.1]. The Frobenius of
${\mathcal O}_{\breve {E}}$
in the sense of [Reference Scholze and WeinsteinSW20, Definition 6.3.1, Appendix to Lecture 19]; see the proof of [Reference Fargues and ScholzeFS21, Proposition II.1.1]. The Frobenius of
![]() $W_{{\mathcal O}_E}(R^+)$
induces an isomorphism
$W_{{\mathcal O}_E}(R^+)$
induces an isomorphism
![]() $ {\mathrm {Frob}} \colon \mathcal {Y}^{[0, \infty )}_S \to \mathcal {Y}^{[0, \infty )}_S $
over
$ {\mathrm {Frob}} \colon \mathcal {Y}^{[0, \infty )}_S \to \mathcal {Y}^{[0, \infty )}_S $
over
![]() ${\mathcal O}_{E}$
. The untilt
${\mathcal O}_{E}$
. The untilt
![]() $S^\sharp $
can be regraded as a (closed) Cartier divisor of
$S^\sharp $
can be regraded as a (closed) Cartier divisor of
![]() $\mathcal {Y}^{[0, \infty )}_S$
; see [Reference Fargues and ScholzeFS21, Proposition II.1.4]. This Cartier divisor is induced by the ideal
$\mathcal {Y}^{[0, \infty )}_S$
; see [Reference Fargues and ScholzeFS21, Proposition II.1.4]. This Cartier divisor is induced by the ideal
![]() $I_{R^{\sharp +}} \subset W_{{\mathcal O}_E}(R^+)$
.
$I_{R^{\sharp +}} \subset W_{{\mathcal O}_E}(R^+)$
.
Remark 5.1.3. For a sousperfectoid adic space X over
![]() ${\mathcal O}_E$
, let
${\mathcal O}_E$
, let
![]() $ {\mathrm {Vect}} (X)$
be the category of vector bundles on X. A G-torsor over X is an exact tensor functor
$ {\mathrm {Vect}} (X)$
be the category of vector bundles on X. A G-torsor over X is an exact tensor functor
![]() $ \mathrm {Rep}_{{\mathcal O}_E}(G) \to {\mathrm {Vect}} (X), $
where
$ \mathrm {Rep}_{{\mathcal O}_E}(G) \to {\mathrm {Vect}} (X), $
where
![]() $\mathrm {Rep}_{{\mathcal O}_E}(G)$
is the category of algebraic representations of G on free
$\mathrm {Rep}_{{\mathcal O}_E}(G)$
is the category of algebraic representations of G on free
![]() ${\mathcal O}_E$
-modules of finite rank. We refer to [Reference Scholze and WeinsteinSW20, Theorem 19.5.2] and [Reference Fargues and ScholzeFS21, Definition/Proposition III.1.1] for equivalent definitions of G-torsors.
${\mathcal O}_E$
-modules of finite rank. We refer to [Reference Scholze and WeinsteinSW20, Theorem 19.5.2] and [Reference Fargues and ScholzeFS21, Definition/Proposition III.1.1] for equivalent definitions of G-torsors.
Definition 5.1.4. A G-shtuka over S with one leg at
![]() $S^\sharp $
is a G-torsor
$S^\sharp $
is a G-torsor
![]() $\mathscr {P}$
over
$\mathscr {P}$
over
![]() $\mathcal {Y}^{[0, \infty )}_S$
with an isomorphism
$\mathcal {Y}^{[0, \infty )}_S$
with an isomorphism
of G-torsors over the open subspace
![]() $\mathcal {Y}^{[0, \infty )}_S \backslash S^{\sharp } \subset \mathcal {Y}^{[0, \infty )}_S$
which is meromorphic along the Cartier divisor
$\mathcal {Y}^{[0, \infty )}_S \backslash S^{\sharp } \subset \mathcal {Y}^{[0, \infty )}_S$
which is meromorphic along the Cartier divisor
![]() $S^{\sharp } \hookrightarrow \mathcal {Y}^{[0, \infty )}_S$
. The meromorphic condition on
$S^{\sharp } \hookrightarrow \mathcal {Y}^{[0, \infty )}_S$
. The meromorphic condition on
![]() $\phi _{\mathscr {P}}$
is defined as in [Reference Scholze and WeinsteinSW20, Definition 5.3.5] (via the Tannakian formalism).
$\phi _{\mathscr {P}}$
is defined as in [Reference Scholze and WeinsteinSW20, Definition 5.3.5] (via the Tannakian formalism).
Remark 5.1.5. Let
![]() $ {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+))$
be the category of finite projective
$ {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+))$
be the category of finite projective
![]() $W_{{\mathcal O}_E}(R^+)$
-modules. We have a natural morphism
$W_{{\mathcal O}_E}(R^+)$
-modules. We have a natural morphism
![]() $ \mathcal {Y}^{[0, \infty )}_S \to \mathrm {Spec}(W_{{\mathcal O}_E}(R^+)) $
of locally ringed spaces. This induces a functor
$ \mathcal {Y}^{[0, \infty )}_S \to \mathrm {Spec}(W_{{\mathcal O}_E}(R^+)) $
of locally ringed spaces. This induces a functor
which in turn induces a functor from the category of G-torsors over
![]() $ \mathrm {Spec} W_{{\mathcal O}_E}(R^+)$
to the category of G-torsors over
$ \mathrm {Spec} W_{{\mathcal O}_E}(R^+)$
to the category of G-torsors over
![]() $\mathcal {Y}^{[0, \infty )}_S$
.
$\mathcal {Y}^{[0, \infty )}_S$
.
In the following, a G-Breuil–Kisin module over
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
in the sense of Definition 2.4.4 is also called a G-Breuil–Kisin module for
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
in the sense of Definition 2.4.4 is also called a G-Breuil–Kisin module for
![]() $R^{\sharp +}$
.
$R^{\sharp +}$
.
Example 5.1.6. Let
![]() $\mathcal {P}_{ {\mathrm {sht}} }$
be the G-torsor over
$\mathcal {P}_{ {\mathrm {sht}} }$
be the G-torsor over
![]() $\mathcal {Y}^{[0, \infty )}_S$
associated with a G-Breuil–Kisin module
$\mathcal {Y}^{[0, \infty )}_S$
associated with a G-Breuil–Kisin module
![]() $\mathcal {P}$
for
$\mathcal {P}$
for
![]() $R^{\sharp +}$
. The isomorphism
$R^{\sharp +}$
. The isomorphism
![]() $ \phi _{\mathcal {P}_{ {\mathrm {sht}} }} \colon ( {\mathrm {Frob}} ^*\mathcal {P}_{ {\mathrm {sht}} })_{ \vert \mathcal {Y}^{[0, \infty )}_S \backslash S^{\sharp }} \overset {\sim }{\to } (\mathcal {P}_{ {\mathrm {sht}} })_{ \vert \mathcal {Y}^{[0, \infty )}_S \backslash S^{\sharp }} $
induced by the Frobenius
$ \phi _{\mathcal {P}_{ {\mathrm {sht}} }} \colon ( {\mathrm {Frob}} ^*\mathcal {P}_{ {\mathrm {sht}} })_{ \vert \mathcal {Y}^{[0, \infty )}_S \backslash S^{\sharp }} \overset {\sim }{\to } (\mathcal {P}_{ {\mathrm {sht}} })_{ \vert \mathcal {Y}^{[0, \infty )}_S \backslash S^{\sharp }} $
induced by the Frobenius
![]() $F_{\mathcal {P}}$
is meromorphic along
$F_{\mathcal {P}}$
is meromorphic along
![]() $S^{\sharp } \hookrightarrow \mathcal {Y}^{[0, \infty )}_S$
. With this isomorphism, we view
$S^{\sharp } \hookrightarrow \mathcal {Y}^{[0, \infty )}_S$
. With this isomorphism, we view
![]() $\mathcal {P}_{ {\mathrm {sht}} }$
as a G-shtuka over S with one leg at
$\mathcal {P}_{ {\mathrm {sht}} }$
as a G-shtuka over S with one leg at
![]() $S^\sharp $
.
$S^\sharp $
.
Following [Reference Scholze and WeinsteinSW20] and [Reference Pappas and RapoportPR24], we introduce some boundedness condition on G-shtukas. First, we fix some notation:
Remark 5.1.7. We assume that S is a geometric point of rank 1; that is,
![]() $S= \mathrm {Spa}(C, {\mathcal O}_C)$
for an algebraically closed nonarchimedean field C over k with ring of integers
$S= \mathrm {Spa}(C, {\mathcal O}_C)$
for an algebraically closed nonarchimedean field C over k with ring of integers
![]() ${\mathcal O}_C$
. Let
${\mathcal O}_C$
. Let
![]() $S^\sharp = \mathrm {Spa}(C^\sharp , {\mathcal O}_{C^\sharp })$
be an untilt of S over
$S^\sharp = \mathrm {Spa}(C^\sharp , {\mathcal O}_{C^\sharp })$
be an untilt of S over
![]() ${\mathcal O}_{\breve {E}}$
. The completed local ring of
${\mathcal O}_{\breve {E}}$
. The completed local ring of
![]() $\mathcal {Y}^{[0, \infty )}_S$
at the closed point
$\mathcal {Y}^{[0, \infty )}_S$
at the closed point
![]() $ \mathrm {Spa}(C^\sharp , {\mathcal O}_{C^\sharp }) \hookrightarrow \mathcal {Y}^{[0, \infty )}_S$
is naturally isomorphic to
$ \mathrm {Spa}(C^\sharp , {\mathcal O}_{C^\sharp }) \hookrightarrow \mathcal {Y}^{[0, \infty )}_S$
is naturally isomorphic to
where
![]() $\xi \in I_{{\mathcal O}_{C^\sharp }}$
is a generator. (See also [Reference Scholze and WeinsteinSW20, Example 15.2.10] and the discussion before it.) We recall that
$\xi \in I_{{\mathcal O}_{C^\sharp }}$
is a generator. (See also [Reference Scholze and WeinsteinSW20, Example 15.2.10] and the discussion before it.) We recall that
![]() $B^+_{ {\mathrm {dR}}}(C^\sharp )$
is a complete discrete valuation ring. The maximal ideal of
$B^+_{ {\mathrm {dR}}}(C^\sharp )$
is a complete discrete valuation ring. The maximal ideal of
![]() $B^+_{ {\mathrm {dR}}}(C^\sharp )$
is generated by
$B^+_{ {\mathrm {dR}}}(C^\sharp )$
is generated by
![]() $\xi $
, and the homomorphism
$\xi $
, and the homomorphism
![]() $\theta $
induces
$\theta $
induces
![]() $B^+_{ {\mathrm {dR}}}(C^\sharp )/\xi \simeq C^\sharp $
. We set
$B^+_{ {\mathrm {dR}}}(C^\sharp )/\xi \simeq C^\sharp $
. We set
![]() $ B_{ {\mathrm {dR}}}(C^\sharp ):=B^+_{ {\mathrm {dR}}}(C^\sharp )[1/\xi ]. $
$ B_{ {\mathrm {dR}}}(C^\sharp ):=B^+_{ {\mathrm {dR}}}(C^\sharp )[1/\xi ]. $
Let
![]() $\mathscr {P}$
be a G-shtuka over S with one leg at
$\mathscr {P}$
be a G-shtuka over S with one leg at
![]() $S^\sharp $
. We write
$S^\sharp $
. We write
![]() $\mathscr {P}_{\vert B^+_{ {\mathrm {dR}}}(C^\sharp )}$
for the restriction of
$\mathscr {P}_{\vert B^+_{ {\mathrm {dR}}}(C^\sharp )}$
for the restriction of
![]() $\mathscr {P}$
to
$\mathscr {P}$
to
![]() $B^+_{ {\mathrm {dR}}}(C^\sharp )$
, which we regard as a G-torsor over
$B^+_{ {\mathrm {dR}}}(C^\sharp )$
, which we regard as a G-torsor over
![]() $ \mathrm {Spec} B^+_{ {\mathrm {dR}}}(C^\sharp )$
. Since
$ \mathrm {Spec} B^+_{ {\mathrm {dR}}}(C^\sharp )$
. Since
![]() $\phi _{\mathscr {P}}$
is meromorphic, it induces an isomorphism
$\phi _{\mathscr {P}}$
is meromorphic, it induces an isomorphism
of G-torsors over
![]() $ \mathrm {Spec} B_{ {\mathrm {dR}}}(C^\sharp )$
, which is denoted by
$ \mathrm {Spec} B_{ {\mathrm {dR}}}(C^\sharp )$
, which is denoted by
![]() $(\phi _{\mathscr {P}})_{ \vert B_{ {\mathrm {dR}}}(C^\sharp )}$
. We note that since
$(\phi _{\mathscr {P}})_{ \vert B_{ {\mathrm {dR}}}(C^\sharp )}$
. We note that since
![]() $C^\sharp $
is algebraically closed, the G-torsor
$C^\sharp $
is algebraically closed, the G-torsor
![]() $\mathscr {P}_{\vert B^+_{ {\mathrm {dR}}}(C^\sharp )}$
is trivial.
$\mathscr {P}_{\vert B^+_{ {\mathrm {dR}}}(C^\sharp )}$
is trivial.
Let
![]() $\mu \colon {\mathbb G}_m \to G_{{\mathcal O}_{\breve {E}}}$
be a minuscule cocharacter.
$\mu \colon {\mathbb G}_m \to G_{{\mathcal O}_{\breve {E}}}$
be a minuscule cocharacter.
Definition 5.1.8. Let
![]() $\mathscr {P}$
be a G-shtuka over S with one leg at
$\mathscr {P}$
be a G-shtuka over S with one leg at
![]() $S^\sharp $
.
$S^\sharp $
.
-
(1) We assume that
 $S = \mathrm {Spa}(C, {\mathcal O}_C)$
is a geometric point of rank 1 with
$S = \mathrm {Spa}(C, {\mathcal O}_C)$
is a geometric point of rank 1 with
 $S^\sharp = \mathrm {Spa}(C^\sharp , {\mathcal O}_{C^\sharp })$
. We say that
$S^\sharp = \mathrm {Spa}(C^\sharp , {\mathcal O}_{C^\sharp })$
. We say that
 $\mathscr {P}$
is bounded by
$\mathscr {P}$
is bounded by
 $\mu $
if for some (and hence all) trivializations
$\mu $
if for some (and hence all) trivializations
 $\mathscr {P}_{ \vert B^+_{ {\mathrm {dR}}}(C^\sharp )} \simeq G_{B^+_{ {\mathrm {dR}}}(C^\sharp )}$
and
$\mathscr {P}_{ \vert B^+_{ {\mathrm {dR}}}(C^\sharp )} \simeq G_{B^+_{ {\mathrm {dR}}}(C^\sharp )}$
and
 $( {\mathrm {Frob}} ^*\mathscr {P})_{ \vert B^+_{ {\mathrm {dR}}}(C^\sharp )} \simeq G_{B^+_{ {\mathrm {dR}}}(C^\sharp )}$
, the isomorphism
$( {\mathrm {Frob}} ^*\mathscr {P})_{ \vert B^+_{ {\mathrm {dR}}}(C^\sharp )} \simeq G_{B^+_{ {\mathrm {dR}}}(C^\sharp )}$
, the isomorphism
 $(\phi _{\mathscr {P}})_{ \vert B_{ {\mathrm {dR}}}(C^\sharp )}$
(see Remark 5.1.7) is given by
$(\phi _{\mathscr {P}})_{ \vert B_{ {\mathrm {dR}}}(C^\sharp )}$
(see Remark 5.1.7) is given by
 $g \mapsto Yg$
for some element Y in the double coset
$g \mapsto Yg$
for some element Y in the double coset  $$\begin{align*}G(B^+_{{\mathrm{dR}}}(C^\sharp))\mu(\xi)^{-1}G(B^+_{{\mathrm{dR}}}(C^\sharp)) \subset G(B_{{\mathrm{dR}}}(C^\sharp)). \end{align*}$$
$$\begin{align*}G(B^+_{{\mathrm{dR}}}(C^\sharp))\mu(\xi)^{-1}G(B^+_{{\mathrm{dR}}}(C^\sharp)) \subset G(B_{{\mathrm{dR}}}(C^\sharp)). \end{align*}$$
-
(2) In general, we say that
 $\mathscr {P}$
is bounded by
$\mathscr {P}$
is bounded by
 $\mu $
if, for any morphism
$\mu $
if, for any morphism
 $ \mathrm {Spa}(C, {\mathcal O}_C) \to S$
with
$ \mathrm {Spa}(C, {\mathcal O}_C) \to S$
with
 $ \mathrm {Spa}(C, {\mathcal O}_C)$
a geometric point of rank 1, the pull-back of
$ \mathrm {Spa}(C, {\mathcal O}_C)$
a geometric point of rank 1, the pull-back of
 $\mathscr {P}$
to
$\mathscr {P}$
to
 $\mathcal {Y}^{[0, \infty )}_{ \mathrm {Spa}(C, {\mathcal O}_C)}$
is bounded by
$\mathcal {Y}^{[0, \infty )}_{ \mathrm {Spa}(C, {\mathcal O}_C)}$
is bounded by
 $\mu $
in the sense of (1).
$\mu $
in the sense of (1).
Notice that we have chosen
![]() $\mu (\xi )^{-1}$
rather than
$\mu (\xi )^{-1}$
rather than
![]() $\mu (\xi )$
; our convention agrees with that of [Reference Pappas and RapoportPR24, Definition 2.4.3].
$\mu (\xi )$
; our convention agrees with that of [Reference Pappas and RapoportPR24, Definition 2.4.3].
Example 5.1.9. Let
![]() $\mu ^{-1}$
be the inverse of
$\mu ^{-1}$
be the inverse of
![]() $\mu $
. If
$\mu $
. If
![]() $\mathcal {P}$
is a G-Breuil–Kisin module for
$\mathcal {P}$
is a G-Breuil–Kisin module for
![]() $R^{\sharp +}$
of type
$R^{\sharp +}$
of type
![]() $\mu ^{-1}$
in the sense of Definition 2.4.4, then the associated G-shtuka
$\mu ^{-1}$
in the sense of Definition 2.4.4, then the associated G-shtuka
![]() $\mathcal {P}_{ {\mathrm {sht}} }$
over S with one leg at
$\mathcal {P}_{ {\mathrm {sht}} }$
over S with one leg at
![]() $S^\sharp $
is bounded by
$S^\sharp $
is bounded by
![]() $\mu $
.
$\mu $
.
The following result can be viewed as a partial converse to Example 5.1.9.
Proposition 5.1.10. Assume that
![]() $S= \mathrm {Spa}(R, R^+)$
is a product of points over k. Let
$S= \mathrm {Spa}(R, R^+)$
is a product of points over k. Let
![]() $\mathcal {P}$
be a G-Breuil–Kisin module for
$\mathcal {P}$
be a G-Breuil–Kisin module for
![]() $R^{\sharp +}$
. Then
$R^{\sharp +}$
. Then
![]() $\mathcal {P}$
is of type
$\mathcal {P}$
is of type
![]() $\mu ^{-1}$
if and only if the associated G-shtuka
$\mu ^{-1}$
if and only if the associated G-shtuka
![]() $\mathcal {P}_{ {\mathrm {sht}} }$
over S with one leg at
$\mathcal {P}_{ {\mathrm {sht}} }$
over S with one leg at
![]() $S^\sharp $
is bounded by
$S^\sharp $
is bounded by
![]() $\mu $
.
$\mu $
.
Proof. We write
![]() $ (R, R^+)=((\prod _{i \in I} C^{+}_i)[1/\varpi ^\flat ], \prod _{i \in I} C^{+}_i). $
Then, as in Example 5.1.2,
$ (R, R^+)=((\prod _{i \in I} C^{+}_i)[1/\varpi ^\flat ], \prod _{i \in I} C^{+}_i). $
Then, as in Example 5.1.2,
![]() $(R^{\sharp }, R^{\sharp +})$
is of the form
$(R^{\sharp }, R^{\sharp +})$
is of the form
![]() $((\prod _{i \in I} C^{\sharp +}_i)[1/\varpi ], \prod _{i \in I} C^{\sharp +}_i)$
. It suffices to prove the ‘if’ direction. By the proof of [Reference ItoIto23, Proposition 5.6.11], it is enough to show that the base change of
$((\prod _{i \in I} C^{\sharp +}_i)[1/\varpi ], \prod _{i \in I} C^{\sharp +}_i)$
. It suffices to prove the ‘if’ direction. By the proof of [Reference ItoIto23, Proposition 5.6.11], it is enough to show that the base change of
![]() $\mathcal {P}$
to
$\mathcal {P}$
to
![]() $(W_{{\mathcal O}_E}(C^{+}_i), I_{C^{\sharp +}_i})$
is of type
$(W_{{\mathcal O}_E}(C^{+}_i), I_{C^{\sharp +}_i})$
is of type
![]() $\mu ^{-1}$
for each
$\mu ^{-1}$
for each
![]() $i \in I$
. Thus, we may assume that the set I is a singleton. We write
$i \in I$
. Thus, we may assume that the set I is a singleton. We write
![]() $(R, R^+)=(C, C^+)$
and
$(R, R^+)=(C, C^+)$
and
![]() $(R^{\sharp }, R^{\sharp +}) =(C^{\sharp }, C^{\sharp +})$
.
$(R^{\sharp }, R^{\sharp +}) =(C^{\sharp }, C^{\sharp +})$
.
We note that
![]() $\mathcal {P}$
is trivial as a G-torsor since
$\mathcal {P}$
is trivial as a G-torsor since
![]() $W_{{\mathcal O}_E}(C^{+})$
is strictly henselian. We fix a trivialization
$W_{{\mathcal O}_E}(C^{+})$
is strictly henselian. We fix a trivialization
![]() $\mathcal {P} \simeq G_{W_{{\mathcal O}_E}(C^{+})}$
, and we set
$\mathcal {P} \simeq G_{W_{{\mathcal O}_E}(C^{+})}$
, and we set
![]() $Y:=F_{\mathcal {P}}(1) \in G(W_{{\mathcal O}_E}(C^{+})[1/\xi ])$
, where
$Y:=F_{\mathcal {P}}(1) \in G(W_{{\mathcal O}_E}(C^{+})[1/\xi ])$
, where
![]() $\xi \in I_{C^{\sharp +}}$
is a generator. Since
$\xi \in I_{C^{\sharp +}}$
is a generator. Since
![]() $\mathcal {P}_{ {\mathrm {sht}} }$
is bounded by
$\mathcal {P}_{ {\mathrm {sht}} }$
is bounded by
![]() $\mu $
, the image of Y under the homomorphism
$\mu $
, the image of Y under the homomorphism
![]() $ G(W_{{\mathcal O}_E}(C^{+})[1/\xi ]) \to G(B_{ {\mathrm {dR}}}(C^\sharp )) $
lies in
$ G(W_{{\mathcal O}_E}(C^{+})[1/\xi ]) \to G(B_{ {\mathrm {dR}}}(C^\sharp )) $
lies in
![]() $G(B^+_{ {\mathrm {dR}}}(C^\sharp ))\mu (\xi )^{-1}G(B^+_{ {\mathrm {dR}}}(C^\sharp ))$
. We want to prove that Y is contained in
$G(B^+_{ {\mathrm {dR}}}(C^\sharp ))\mu (\xi )^{-1}G(B^+_{ {\mathrm {dR}}}(C^\sharp ))$
. We want to prove that Y is contained in
To simplify the notation, we write
![]() $A:=W_{{\mathcal O}_E}(C^{+})$
and
$A:=W_{{\mathcal O}_E}(C^{+})$
and
![]() $B^+:=B^+_{ {\mathrm {dR}}}(C^\sharp )$
. The homomorphism
$B^+:=B^+_{ {\mathrm {dR}}}(C^\sharp )$
. The homomorphism
![]() $A/\xi \to B^+/\xi $
can be identified with
$A/\xi \to B^+/\xi $
can be identified with
![]() $C^{\sharp +} \to C^\sharp $
, and hence, it is injective. It follows that
$C^{\sharp +} \to C^\sharp $
, and hence, it is injective. It follows that
![]() $A \to B^+$
is injective, and we have
$A \to B^+$
is injective, and we have
![]() $A=A[1/\xi ] \cap B^+$
. This implies that the natural map
$A=A[1/\xi ] \cap B^+$
. This implies that the natural map
![]() $ G(A[1/\xi ])/G(A) \to G(B^+[1/\xi ])/G(B^+) $
is injective. We claim that this map induces the following bijection:
$ G(A[1/\xi ])/G(A) \to G(B^+[1/\xi ])/G(B^+) $
is injective. We claim that this map induces the following bijection:
This claim implies that
![]() $Y \in G(A)\mu (\xi )^{-1}G(A)$
, as desired.
$Y \in G(A)\mu (\xi )^{-1}G(A)$
, as desired.
We shall prove the claim. The map
![]() $ G(A)\mu (\xi )^{-1}G(A)/G(A) \to G(A)/G_\mu (A, (\xi )) $
defined by
$ G(A)\mu (\xi )^{-1}G(A)/G(A) \to G(A)/G_\mu (A, (\xi )) $
defined by
![]() $g\mu (\xi )^{-1}G(A) \mapsto gG_\mu (A, (\xi ))$
is bijective. By Proposition 2.3.3, we have
$g\mu (\xi )^{-1}G(A) \mapsto gG_\mu (A, (\xi ))$
is bijective. By Proposition 2.3.3, we have
![]() $G(A)/G_\mu (A, (\xi )) \overset {\sim }{\to } G(C^{\sharp +})/P_\mu (C^{\sharp +})$
. Similarly, we have
$G(A)/G_\mu (A, (\xi )) \overset {\sim }{\to } G(C^{\sharp +})/P_\mu (C^{\sharp +})$
. Similarly, we have
(We note that the results of Section 2.3 apply to the pair
![]() $(B^+, (\xi ))$
.) It then suffices to prove that the map
$(B^+, (\xi ))$
.) It then suffices to prove that the map
is bijective. This follows from the valuative criterion and the properness of the scheme
![]() $G_{{\mathcal O}_{\breve {E}}}/P_\mu $
over
$G_{{\mathcal O}_{\breve {E}}}/P_\mu $
over
![]() $ \mathrm {Spec} {\mathcal O}_{\breve {E}}$
. (We also use that the field
$ \mathrm {Spec} {\mathcal O}_{\breve {E}}$
. (We also use that the field
![]() $C^\sharp $
is algebraically closed and that the valuation ring
$C^\sharp $
is algebraically closed and that the valuation ring
![]() $C^{\sharp +}$
is strictly henselian.)
$C^{\sharp +}$
is strictly henselian.)
We define an open subset
We collect some results on
![]() $\mathcal {Y}^{[0, \infty ]}_S$
that will be needed in the sequel.
$\mathcal {Y}^{[0, \infty ]}_S$
that will be needed in the sequel.
Remark 5.1.11. As explained in [Reference Scholze and WeinsteinSW20, Proposition 13.1.1] and [Reference KedlayaKed20] (see also [Reference Pappas and RapoportPR24, Section 2.1]), we can regard
![]() $\mathcal {Y}^{[0, \infty ]}_S$
as a sousperfectoid adic space. More precisely, we consider the following rational open subsets of
$\mathcal {Y}^{[0, \infty ]}_S$
as a sousperfectoid adic space. More precisely, we consider the following rational open subsets of
![]() $ \mathrm {Spa}(W_{{\mathcal O}_E}(R^+))$
:
$ \mathrm {Spa}(W_{{\mathcal O}_E}(R^+))$
:
 $$ \begin{align*} U&:= \{ \, x \in \mathrm{Spa}(W_{{\mathcal O}_E}(R^+)) \, \vert \, \vert [\varpi^\flat](x) \vert \leq \vert \pi(x) \vert \neq 0 \, \},\\ V&:= \{ \, x \in \mathrm{Spa}(W_{{\mathcal O}_E}(R^+)) \, \vert \, \vert \pi(x) \vert \leq \vert [\varpi^\flat](x) \vert \neq 0 \, \}. \end{align*} $$
$$ \begin{align*} U&:= \{ \, x \in \mathrm{Spa}(W_{{\mathcal O}_E}(R^+)) \, \vert \, \vert [\varpi^\flat](x) \vert \leq \vert \pi(x) \vert \neq 0 \, \},\\ V&:= \{ \, x \in \mathrm{Spa}(W_{{\mathcal O}_E}(R^+)) \, \vert \, \vert \pi(x) \vert \leq \vert [\varpi^\flat](x) \vert \neq 0 \, \}. \end{align*} $$
By the proof of [Reference KedlayaKed20, Proposition 3.6], both U and V are sousperfectoid adic spaces. We can glue them along
![]() $U\cap V$
and endow
$U\cap V$
and endow
![]() $\mathcal {Y}^{[0, \infty ]}_S$
with the structure of a sousperfectoid adic space. Strictly speaking, only the case where
$\mathcal {Y}^{[0, \infty ]}_S$
with the structure of a sousperfectoid adic space. Strictly speaking, only the case where
![]() ${\mathcal O}_E={\mathbb Z}_p$
is considered in [Reference KedlayaKed20]. However, it is easy to see that the same argument works for general
${\mathcal O}_E={\mathbb Z}_p$
is considered in [Reference KedlayaKed20]. However, it is easy to see that the same argument works for general
![]() ${\mathcal O}_E$
.
${\mathcal O}_E$
.
Remark 5.1.12. Let
![]() $ j^* \colon {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+)) \to {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ]}_S) $
be the functor induced by the natural morphism
$ j^* \colon {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+)) \to {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ]}_S) $
be the functor induced by the natural morphism
![]() $ j \colon \mathcal {Y}^{[0, \infty ]}_S \to \mathrm {Spec}(W_{{\mathcal O}_E}(R^+)) $
of locally ringed spaces. We claim that
$ j \colon \mathcal {Y}^{[0, \infty ]}_S \to \mathrm {Spec}(W_{{\mathcal O}_E}(R^+)) $
of locally ringed spaces. We claim that
![]() $j^*$
is fully faithful. Indeed, the morphism j factors through the open subscheme
$j^*$
is fully faithful. Indeed, the morphism j factors through the open subscheme
Thus,
![]() $j^*$
can be written as the composition
$j^*$
can be written as the composition
where
![]() $ {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S)$
is the category of vector bundles on the scheme
$ {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S)$
is the category of vector bundles on the scheme
![]() $\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S$
. Since we have
$\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S$
. Since we have
![]() $W_{{\mathcal O}_E}(R^+) = {\mathcal O}_{\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S}(\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S)$
, the first functor is fully faithful. The second functor is an equivalence by [Reference KedlayaKed20, Theorem 3.8] (again, the result holds for general
$W_{{\mathcal O}_E}(R^+) = {\mathcal O}_{\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S}(\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S)$
, the first functor is fully faithful. The second functor is an equivalence by [Reference KedlayaKed20, Theorem 3.8] (again, the result holds for general
![]() ${\mathcal O}_E$
by the same argument), and hence, the claim follows. The second equivalence is also an exact equivalence of exact categories (cf. [Reference GleasonGle22a, Remark 2.3]).
${\mathcal O}_E$
by the same argument), and hence, the claim follows. The second equivalence is also an exact equivalence of exact categories (cf. [Reference GleasonGle22a, Remark 2.3]).
Let
![]() $\xi \in I_{R^{\sharp +}}$
be a generator. For finite projective
$\xi \in I_{R^{\sharp +}}$
be a generator. For finite projective
![]() $W_{{\mathcal O}_E}(R^+)$
-modules M and N, the functor
$W_{{\mathcal O}_E}(R^+)$
-modules M and N, the functor
![]() $j^*$
induces a bijection between the set of isomorphisms
$j^*$
induces a bijection between the set of isomorphisms
![]() $M[1/\xi ] \overset {\sim }{\to } N[1/\xi ]$
and the set of isomorphisms
$M[1/\xi ] \overset {\sim }{\to } N[1/\xi ]$
and the set of isomorphisms
![]() $ (j^*M)_{\vert \mathcal {Y}^{[0, \infty ]}_S \backslash S^{\sharp }} \overset {\sim }{\to } (j^*N)_{\vert \mathcal {Y}^{[0, \infty ]}_S \backslash S^{\sharp }} $
which are meromorphic.
$ (j^*M)_{\vert \mathcal {Y}^{[0, \infty ]}_S \backslash S^{\sharp }} \overset {\sim }{\to } (j^*N)_{\vert \mathcal {Y}^{[0, \infty ]}_S \backslash S^{\sharp }} $
which are meromorphic.
The following result is obtained in [Reference GleasonGle21, Section 2.1.2] (in the more general case where G is parahoric).
Proposition 5.1.13. Assume that
![]() $S= \mathrm {Spa}(R, R^+)$
is a product of points over k. Then the functor
$S= \mathrm {Spa}(R, R^+)$
is a product of points over k. Then the functor
![]() $j^* \colon {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+)) \to {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ]}_S)$
induces an equivalence from the category of G-torsors over
$j^* \colon {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+)) \to {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ]}_S)$
induces an equivalence from the category of G-torsors over
![]() $ \mathrm {Spec} W_{{\mathcal O}_E}(R^+)$
to that of G-torsors over
$ \mathrm {Spec} W_{{\mathcal O}_E}(R^+)$
to that of G-torsors over
![]() $\mathcal {Y}^{[0, \infty ]}_S$
.
$\mathcal {Y}^{[0, \infty ]}_S$
.
Proof. We briefly recall the argument for the convenience of the reader. By Remark 5.1.12, it suffices to prove that the restriction functor from the category of G-torsors over
![]() $ \mathrm {Spec} W_{{\mathcal O}_E}(R^+)$
to that of G-torsors over
$ \mathrm {Spec} W_{{\mathcal O}_E}(R^+)$
to that of G-torsors over
![]() $\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S$
is an equivalence.
$\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S$
is an equivalence.
By the proof of [Reference GleasonGle21, Proposition 2.1.17], we see that the functor
![]() $ {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+)) \to {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S) $
is an equivalence. (This is proved in [Reference KedlayaKed20, Theorem 2.7] if
$ {\mathrm {Vect}} (W_{{\mathcal O}_E}(R^+)) \to {\mathrm {Vect}} (\mathcal {Y}^{[0, \infty ], {\mathrm {alg}} }_S) $
is an equivalence. (This is proved in [Reference KedlayaKed20, Theorem 2.7] if
![]() $S= \mathrm {Spa}(C, C^+)$
for an algebraically closed nonarchimedean field C over k, and the general case can be deduced from this special case.) Then the assertion follows from [Reference AnschützAns22, Proposition 8.5] since we assume that G is reductive here.
$S= \mathrm {Spa}(C, C^+)$
for an algebraically closed nonarchimedean field C over k, and the general case can be deduced from this special case.) Then the assertion follows from [Reference AnschützAns22, Proposition 8.5] since we assume that G is reductive here.
The Frobenius of
![]() $W_{{\mathcal O}_E}(R^+)$
induces an isomorphism
$W_{{\mathcal O}_E}(R^+)$
induces an isomorphism
![]() $ {\mathrm {Frob}} \colon \mathcal {Y}^{[0, \infty ]}_S \to \mathcal {Y}^{[0, \infty ]}_S $
over
$ {\mathrm {Frob}} \colon \mathcal {Y}^{[0, \infty ]}_S \to \mathcal {Y}^{[0, \infty ]}_S $
over
![]() ${\mathcal O}_{E}$
. It will be convenient to make the following definition:
${\mathcal O}_{E}$
. It will be convenient to make the following definition:
Definition 5.1.14. An extended G-shtuka over S with one leg at
![]() $S^{\sharp }$
is a G-torsor
$S^{\sharp }$
is a G-torsor
![]() $\widetilde {\mathscr {P}}$
over
$\widetilde {\mathscr {P}}$
over
![]() $\mathcal {Y}^{[0, \infty ]}_S$
with an isomorphism
$\mathcal {Y}^{[0, \infty ]}_S$
with an isomorphism
which is meromorphic along
![]() $S^{\sharp } \hookrightarrow \mathcal {Y}^{[0, \infty ]}_S$
.
$S^{\sharp } \hookrightarrow \mathcal {Y}^{[0, \infty ]}_S$
.
As in Example 5.1.6, to a G-Breuil–Kisin module
![]() $\mathcal {P}$
for
$\mathcal {P}$
for
![]() $R^{\sharp +}$
, we can attach an extended G-shtuka
$R^{\sharp +}$
, we can attach an extended G-shtuka
![]() $\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
over S with one leg at
$\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
over S with one leg at
![]() $S^{\sharp }$
.
$S^{\sharp }$
.
Corollary 5.1.15. The functor
![]() $\mathcal {P} \mapsto \widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
from the groupoid of G-Breuil–Kisin modules for
$\mathcal {P} \mapsto \widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
from the groupoid of G-Breuil–Kisin modules for
![]() $R^{\sharp +}$
to that of extended G-shtukas over S with one leg at
$R^{\sharp +}$
to that of extended G-shtukas over S with one leg at
![]() $S^{\sharp }$
is fully faithful. If S is a product of points over k, then the functor is an equivalence.
$S^{\sharp }$
is fully faithful. If S is a product of points over k, then the functor is an equivalence.
Proof. The first assertion follows from Remark 5.1.12. The second assertion follows from Remark 5.1.12 and Proposition 5.1.13.
Proposition 5.1.16 (cf. [Reference Pappas and RapoportPR24, Proposition 2.4.6]).
Assume that
![]() $S= \mathrm {Spa}(C, {\mathcal O}_C)$
is a geometric point of rank
$S= \mathrm {Spa}(C, {\mathcal O}_C)$
is a geometric point of rank
![]() $1$
with
$1$
with
![]() $S^{\sharp }= \mathrm {Spa}(C^{\sharp }, {\mathcal O}_{C^\sharp })$
. Then the construction
$S^{\sharp }= \mathrm {Spa}(C^{\sharp }, {\mathcal O}_{C^\sharp })$
. Then the construction
![]() $\mathcal {P} \mapsto \mathcal {P}_{ {\mathrm {sht}} }$
induces an equivalence of groupoids:
$\mathcal {P} \mapsto \mathcal {P}_{ {\mathrm {sht}} }$
induces an equivalence of groupoids:
 $$\begin{align*}\left\{ \begin{array}{c} \displaystyle G\text{-Breuil--Kisin modules for } {\mathcal O}_{C^\sharp} \end{array} \right\} \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle G\text{-shtukas over } \mathrm{Spa}(C, {\mathcal O}_C) \\ \displaystyle \text{with one leg at } \mathrm{Spa}(C^{\sharp}, {\mathcal O}_{C^\sharp}) \end{array} \right\}. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{c} \displaystyle G\text{-Breuil--Kisin modules for } {\mathcal O}_{C^\sharp} \end{array} \right\} \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle G\text{-shtukas over } \mathrm{Spa}(C, {\mathcal O}_C) \\ \displaystyle \text{with one leg at } \mathrm{Spa}(C^{\sharp}, {\mathcal O}_{C^\sharp}) \end{array} \right\}. \end{align*}$$
Moreover, this equivalence induces
 $$\begin{align*}\left\{ \begin{array}{c} \displaystyle G\text{-}\mu^{-1}\text{-displays} \\ \text{over } (W_{{\mathcal O}_E}({\mathcal O}_C), I_{{\mathcal O}_{C^\sharp}}) \end{array} \right\} \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle G\text{-shtukas over } \mathrm{Spa}(C, {\mathcal O}_C) \\ \displaystyle \text{with one leg at } \mathrm{Spa}(C^{\sharp}, {\mathcal O}_{C^\sharp}) \\ \displaystyle \text{which are bounded by } \mu \end{array} \right\}. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{c} \displaystyle G\text{-}\mu^{-1}\text{-displays} \\ \text{over } (W_{{\mathcal O}_E}({\mathcal O}_C), I_{{\mathcal O}_{C^\sharp}}) \end{array} \right\} \overset{\sim}{\to} \left\{ \begin{array}{c} \displaystyle G\text{-shtukas over } \mathrm{Spa}(C, {\mathcal O}_C) \\ \displaystyle \text{with one leg at } \mathrm{Spa}(C^{\sharp}, {\mathcal O}_{C^\sharp}) \\ \displaystyle \text{which are bounded by } \mu \end{array} \right\}. \end{align*}$$
Proof. Although this result is not used in the rest of this paper, we include a proof for completeness. By Proposition 2.4.5 and Proposition 5.1.10, it suffices to prove the first assertion. By [Reference Pappas and RapoportPR24, Proposition 2.2.7] (which holds for general
![]() ${\mathcal O}_E$
by the same argument), the functor is fully faithful. As in [Reference Pappas and RapoportPR24, Proposition 2.4.6], we can extend a G-shtuka
${\mathcal O}_E$
by the same argument), the functor is fully faithful. As in [Reference Pappas and RapoportPR24, Proposition 2.4.6], we can extend a G-shtuka
![]() $\mathscr {P}$
over S with one leg at
$\mathscr {P}$
over S with one leg at
![]() $S^\sharp $
to an extended G-shtuka
$S^\sharp $
to an extended G-shtuka
![]() $\widetilde {\mathscr {P}}$
, by using Fargues’ classification [Reference FarguesFar20] of G-torsors over the Fargues–Fontaine curve (see also [Reference AnschützAns19]). By Corollary 5.1.15, it then follows that the functor is essentially surjective.
$\widetilde {\mathscr {P}}$
, by using Fargues’ classification [Reference FarguesFar20] of G-torsors over the Fargues–Fontaine curve (see also [Reference AnschützAns19]). By Corollary 5.1.15, it then follows that the functor is essentially surjective.
5.2 Quasi-isogenies
Let
![]() $S= \mathrm {Spa}(R, R^+)$
be an affinoid perfectoid space over k, and let
$S= \mathrm {Spa}(R, R^+)$
be an affinoid perfectoid space over k, and let
![]() $S^\sharp = \mathrm {Spa}(R^\sharp , R^{\sharp +})$
be an untilt of S over
$S^\sharp = \mathrm {Spa}(R^\sharp , R^{\sharp +})$
be an untilt of S over
![]() ${\mathcal O}_{\breve {E}}$
. We fix a pseudo-uniformizer
${\mathcal O}_{\breve {E}}$
. We fix a pseudo-uniformizer
![]() $\varpi ^\flat \in R^+$
.
$\varpi ^\flat \in R^+$
.
For an integer
![]() $n \geq 1$
, we define a rational open subset
$n \geq 1$
, we define a rational open subset
We set
![]() $ \mathcal {Y}^{[n, \infty )}_S:=\mathcal {Y}^{[0, \infty )}_S \cap \mathcal {Y}^{[n, \infty ]}_S. $
For the isomorphism
$ \mathcal {Y}^{[n, \infty )}_S:=\mathcal {Y}^{[0, \infty )}_S \cap \mathcal {Y}^{[n, \infty ]}_S. $
For the isomorphism
![]() $ {\mathrm {Frob}} \colon \mathcal {Y}^{[0, \infty ]}_S \to \mathcal {Y}^{[0, \infty ]}_S$
, the equality
$ {\mathrm {Frob}} \colon \mathcal {Y}^{[0, \infty ]}_S \to \mathcal {Y}^{[0, \infty ]}_S$
, the equality
![]() $ {\mathrm {Frob}} (\mathcal {Y}^{[n, \infty ]}_S)=\mathcal {Y}^{[qn, \infty ]}_S$
holds. Similarly, we have
$ {\mathrm {Frob}} (\mathcal {Y}^{[n, \infty ]}_S)=\mathcal {Y}^{[qn, \infty ]}_S$
holds. Similarly, we have
![]() $ {\mathrm {Frob}} (\mathcal {Y}^{[n, \infty )}_S)=\mathcal {Y}^{[qn, \infty )}_S$
.
$ {\mathrm {Frob}} (\mathcal {Y}^{[n, \infty )}_S)=\mathcal {Y}^{[qn, \infty )}_S$
.
Definition 5.2.1. Let
![]() $\mathcal {P}_0$
be a G-Breuil–Kisin module over
$\mathcal {P}_0$
be a G-Breuil–Kisin module over
![]() $({\mathcal O}_{\breve {E}}, (\pi ))$
and
$({\mathcal O}_{\breve {E}}, (\pi ))$
and
![]() $\mathscr {P}$
a G-shtuka over S with one leg at
$\mathscr {P}$
a G-shtuka over S with one leg at
![]() $S^\sharp $
. A quasi-isogeny from
$S^\sharp $
. A quasi-isogeny from
![]() $\mathscr {P}$
to
$\mathscr {P}$
to
![]() $\mathcal {P}_0$
is an element of the set
$\mathcal {P}_0$
is an element of the set
where n runs over all integers
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $\mathcal {Y}^{[n, \infty )}_S$
does not intersect with
$\mathcal {Y}^{[n, \infty )}_S$
does not intersect with
![]() $S^\sharp $
. Here,
$S^\sharp $
. Here,
![]() $(\mathcal {P}_0)_{\vert \mathcal {Y}^{[n, \infty )}_S}$
is the pull-back of
$(\mathcal {P}_0)_{\vert \mathcal {Y}^{[n, \infty )}_S}$
is the pull-back of
![]() $\mathcal {P}_0$
along the morphism
$\mathcal {P}_0$
along the morphism
![]() $\mathcal {Y}^{[n, \infty )}_S \to \mathrm {Spec} {\mathcal O}_{\breve {E}}$
of locally ringed spaces. Similarly, for an extended G-shtuka
$\mathcal {Y}^{[n, \infty )}_S \to \mathrm {Spec} {\mathcal O}_{\breve {E}}$
of locally ringed spaces. Similarly, for an extended G-shtuka
![]() $\widetilde {\mathscr {P}}$
over S with one leg at
$\widetilde {\mathscr {P}}$
over S with one leg at
![]() $S^{\sharp }$
, we define a quasi-isogeny from
$S^{\sharp }$
, we define a quasi-isogeny from
![]() $\widetilde {\mathscr {P}}$
to
$\widetilde {\mathscr {P}}$
to
![]() $\mathcal {P}_0$
as an element of the set
$\mathcal {P}_0$
as an element of the set
where n runs over all integers
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $\mathcal {Y}^{[n, \infty ]}_S$
does not intersect with
$\mathcal {Y}^{[n, \infty ]}_S$
does not intersect with
![]() $S^\sharp $
.
$S^\sharp $
.
Remark 5.2.2. Let
![]() $\mathscr {P}$
be a G-shtuka over S with one leg at
$\mathscr {P}$
be a G-shtuka over S with one leg at
![]() $S^\sharp $
. Using a quasi-isogeny from
$S^\sharp $
. Using a quasi-isogeny from
![]() $\mathscr {P}$
to
$\mathscr {P}$
to
![]() $\mathcal {P}_0$
, we can extend
$\mathcal {P}_0$
, we can extend
![]() $\mathscr {P}$
to an extended G-shtuka over S with one leg at
$\mathscr {P}$
to an extended G-shtuka over S with one leg at
![]() $S^{\sharp }$
. It follows that the restriction functor from the groupoid of extended G-shtukas
$S^{\sharp }$
. It follows that the restriction functor from the groupoid of extended G-shtukas
![]() $\widetilde {\mathscr {P}}$
over S with one leg at
$\widetilde {\mathscr {P}}$
over S with one leg at
![]() $S^\sharp $
together with a quasi-isogeny from
$S^\sharp $
together with a quasi-isogeny from
![]() $\widetilde {\mathscr {P}}$
to
$\widetilde {\mathscr {P}}$
to
![]() $\mathcal {P}_0$
to the groupoid of G-shtukas
$\mathcal {P}_0$
to the groupoid of G-shtukas
![]() $\mathscr {P}$
over S with one leg at
$\mathscr {P}$
over S with one leg at
![]() $S^\sharp $
together with a quasi-isogeny from
$S^\sharp $
together with a quasi-isogeny from
![]() $\mathscr {P}$
to
$\mathscr {P}$
to
![]() $\mathcal {P}_0$
is an equivalence.
$\mathcal {P}_0$
is an equivalence.
We want to relate quasi-isogenies of (extended) G-shtukas to quasi-isogenies of G-Breuil–Kisin modules, which we define as follows:
Definition 5.2.3. Let
![]() $(A, (\pi ))$
be an
$(A, (\pi ))$
be an
![]() ${\mathcal O}_E$
-prism. Let
${\mathcal O}_E$
-prism. Let
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {P}'$
be G-Breuil–Kisin modules over
$\mathcal {P}'$
be G-Breuil–Kisin modules over
![]() $(A, (\pi ))$
. A quasi-isogeny from
$(A, (\pi ))$
. A quasi-isogeny from
![]() $\mathcal {P}$
to
$\mathcal {P}$
to
![]() $\mathcal {P}'$
is a Frobenius equivariant isomorphism
$\mathcal {P}'$
is a Frobenius equivariant isomorphism
of G-torsors over
![]() $ \mathrm {Spec} A[1/\pi ]$
. If
$ \mathrm {Spec} A[1/\pi ]$
. If
![]() $\eta $
arises from a (unique) isomorphism
$\eta $
arises from a (unique) isomorphism
![]() $\mathcal {P} \overset {\sim }{\to } \mathcal {P}'$
of G-Breuil–Kisin modules over
$\mathcal {P} \overset {\sim }{\to } \mathcal {P}'$
of G-Breuil–Kisin modules over
![]() $(A, (\pi ))$
, we say that
$(A, (\pi ))$
, we say that
![]() $\eta $
is effective. In this case, the isomorphism
$\eta $
is effective. In this case, the isomorphism
![]() $\mathcal {P} \overset {\sim }{\to } \mathcal {P}'$
is denoted by the same symbol
$\mathcal {P} \overset {\sim }{\to } \mathcal {P}'$
is denoted by the same symbol
![]() $\eta $
.
$\eta $
.
We assume that
![]() $\pi =0$
in
$\pi =0$
in
![]() $R^{\sharp +}/\varpi $
, or equivalently,
$R^{\sharp +}/\varpi $
, or equivalently,
![]() $\pi \in I_{R^{\sharp +}}$
, where
$\pi \in I_{R^{\sharp +}}$
, where
![]() $\varpi :=\theta ([\varpi ^\flat ]) \in R^{\sharp +}$
. By [Reference ItoIto23, Lemma 2.3.3], we have
$\varpi :=\theta ([\varpi ^\flat ]) \in R^{\sharp +}$
. By [Reference ItoIto23, Lemma 2.3.3], we have
![]() $I_{R^{\sharp +}}=(\pi )$
in
$I_{R^{\sharp +}}=(\pi )$
in
![]() $W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ]$
. We use the following notation. For an integer
$W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ]$
. We use the following notation. For an integer
![]() $m \geq 0$
, we set
$m \geq 0$
, we set
where
![]() $[\varpi ^\flat ]^{1/q^m}:=[(\varpi ^\flat )^{1/q^m}]$
. We write
$[\varpi ^\flat ]^{1/q^m}:=[(\varpi ^\flat )^{1/q^m}]$
. We write
![]() $A=A_0$
. Let
$A=A_0$
. Let
where
![]() $ R^+_{ {\mathrm {red}} }:= \varinjlim _{m} R^+/(\varpi ^\flat )^{1/q^m}. $
For a G-Breuil–Kisin module
$ R^+_{ {\mathrm {red}} }:= \varinjlim _{m} R^+/(\varpi ^\flat )^{1/q^m}. $
For a G-Breuil–Kisin module
![]() $\mathcal {P}$
over
$\mathcal {P}$
over
![]() $(A, (\pi ))$
, the base change of
$(A, (\pi ))$
, the base change of
![]() $\mathcal {P}$
to
$\mathcal {P}$
to
![]() $(A_m, (\pi ))$
(resp.
$(A_m, (\pi ))$
(resp.
![]() $(A_{ {\mathrm {red}} }, (\pi ))$
) is denoted by
$(A_{ {\mathrm {red}} }, (\pi ))$
) is denoted by
![]() $\mathcal {P}_m$
(resp.
$\mathcal {P}_m$
(resp.
![]() $\mathcal {P}_{ {\mathrm {red}} }$
). We use the same notation for quasi-isogenies (or isomorphisms).
$\mathcal {P}_{ {\mathrm {red}} }$
). We use the same notation for quasi-isogenies (or isomorphisms).
Lemma 5.2.4. Let
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {P}'$
be G-Breuil–Kisin modules over
$\mathcal {P}'$
be G-Breuil–Kisin modules over
![]() $(A, (\pi ))$
. The map
$(A, (\pi ))$
. The map
is bijective for every
![]() $m \geq 1$
.
$m \geq 1$
.
Proof. By the Tannakian formalism, we are reduced to proving the following claim (by applying it to internal homs): Let M be a finite projective A-module with an isomorphism
![]() $F_M \colon (\phi ^*M)[1/\pi ] \overset {\sim }{\to } M[1/\pi ]$
. Then the natural homomorphism
$F_M \colon (\phi ^*M)[1/\pi ] \overset {\sim }{\to } M[1/\pi ]$
. Then the natural homomorphism
is bijective. This is easy to see since the kernel of
![]() $A \to A_m$
is killed by
$A \to A_m$
is killed by
![]() $\phi ^m$
.
$\phi ^m$
.
Lemma 5.2.5. Let
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {P}'$
be G-Breuil–Kisin modules over
$\mathcal {P}'$
be G-Breuil–Kisin modules over
![]() $(A, (\pi ))$
such that
$(A, (\pi ))$
such that
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {P}'$
are trivial as G-torsors over
$\mathcal {P}'$
are trivial as G-torsors over
![]() $ \mathrm {Spec} A$
. Let
$ \mathrm {Spec} A$
. Let
![]() $\eta \colon \mathcal {P}[1/\pi ] \overset {\sim }{\to } \mathcal {P}'[1/\pi ]$
be a quasi-isogeny. If the base change
$\eta \colon \mathcal {P}[1/\pi ] \overset {\sim }{\to } \mathcal {P}'[1/\pi ]$
be a quasi-isogeny. If the base change
![]() $\eta _{ {\mathrm {red}} } \colon \mathcal {P}_{ {\mathrm {red}} }[1/\pi ] \overset {\sim }{\to } \mathcal {P}^{\prime }_{ {\mathrm {red}} }[1/\pi ]$
is effective, then there exists an integer
$\eta _{ {\mathrm {red}} } \colon \mathcal {P}_{ {\mathrm {red}} }[1/\pi ] \overset {\sim }{\to } \mathcal {P}^{\prime }_{ {\mathrm {red}} }[1/\pi ]$
is effective, then there exists an integer
![]() $m \geq 1$
such that
$m \geq 1$
such that
![]() $ \eta _m \colon \mathcal {P}_{m}[1/\pi ] \overset {\sim }{\to } \mathcal {P}^{\prime }_{m}[1/\pi ] $
is effective.
$ \eta _m \colon \mathcal {P}_{m}[1/\pi ] \overset {\sim }{\to } \mathcal {P}^{\prime }_{m}[1/\pi ] $
is effective.
Proof. We fix trivializations
![]() $\mathcal {P} \simeq G_A$
and
$\mathcal {P} \simeq G_A$
and
![]() $\mathcal {P}' \simeq G_A$
. Then
$\mathcal {P}' \simeq G_A$
. Then
![]() $\eta $
is identified with an element
$\eta $
is identified with an element
![]() $g \in G(A[1/\pi ])$
whose image in
$g \in G(A[1/\pi ])$
whose image in
![]() $G(A_{ {\mathrm {red}} }[1/\pi ])$
lies in
$G(A_{ {\mathrm {red}} }[1/\pi ])$
lies in
![]() $G(A_{ {\mathrm {red}} })$
. We want to show that the image of g in
$G(A_{ {\mathrm {red}} })$
. We want to show that the image of g in
![]() $G(A_m[1/\pi ])$
belongs to
$G(A_m[1/\pi ])$
belongs to
![]() $G(A_m)$
for some
$G(A_m)$
for some
![]() $m \geq 1$
. Since G is an affine scheme of finite type over
$m \geq 1$
. Since G is an affine scheme of finite type over
![]() ${\mathcal O}_E$
, it suffices to prove that for an element
${\mathcal O}_E$
, it suffices to prove that for an element
![]() $x \in A$
whose image
$x \in A$
whose image
![]() $x_{ {\mathrm {red}} } \in A_{ {\mathrm {red}} }$
is divisible by
$x_{ {\mathrm {red}} } \in A_{ {\mathrm {red}} }$
is divisible by
![]() $\pi $
, there exists an integer
$\pi $
, there exists an integer
![]() $m \geq 1$
such that the image
$m \geq 1$
such that the image
![]() $x_{m} \in A_m$
is also divisible by
$x_{m} \in A_m$
is also divisible by
![]() $\pi $
. This is clear since
$\pi $
. This is clear since
![]() $R^+_{ {\mathrm {red}} }= \varinjlim _{m} R^+/(\varpi ^\flat )^{1/q^m}$
.
$R^+_{ {\mathrm {red}} }= \varinjlim _{m} R^+/(\varpi ^\flat )^{1/q^m}$
.
We define
![]() $B^{[n, \infty ]}_S:={\mathcal O}_{\mathcal {Y}^{[n, \infty ]}_S}(\mathcal {Y}^{[n, \infty ]}_S)$
, which is a
$B^{[n, \infty ]}_S:={\mathcal O}_{\mathcal {Y}^{[n, \infty ]}_S}(\mathcal {Y}^{[n, \infty ]}_S)$
, which is a
![]() $W_{{\mathcal O}_E}(R^+)[1/\pi ]$
-algebra. The universal property of the rational open subset
$W_{{\mathcal O}_E}(R^+)[1/\pi ]$
-algebra. The universal property of the rational open subset
![]() $\mathcal {Y}^{[n, \infty ]}_S$
(by applying it to the affinoid ring
$\mathcal {Y}^{[n, \infty ]}_S$
(by applying it to the affinoid ring
![]() $(A[1/\pi ], A[1/\pi ]^{\circ })$
) induces a natural homomorphism
$(A[1/\pi ], A[1/\pi ]^{\circ })$
) induces a natural homomorphism
such that the composition
![]() $ W_{{\mathcal O}_E}(R^+)[1/\pi ] \to B^{[n, \infty ]}_S \to (W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ])[1/\pi ] $
coincides with the quotient map.
$ W_{{\mathcal O}_E}(R^+)[1/\pi ] \to B^{[n, \infty ]}_S \to (W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ])[1/\pi ] $
coincides with the quotient map.
Let
![]() $\mathcal {P}_0$
be a G-Breuil–Kisin module over
$\mathcal {P}_0$
be a G-Breuil–Kisin module over
![]() $({\mathcal O}_{\breve {E}}, (\pi ))$
and let
$({\mathcal O}_{\breve {E}}, (\pi ))$
and let
![]() $\mathcal {P}$
be a G-Breuil–Kisin module over
$\mathcal {P}$
be a G-Breuil–Kisin module over
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
. We assume that
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
. We assume that
![]() $\mathcal {P}$
is trivial as a G-torsor. We denote by
$\mathcal {P}$
is trivial as a G-torsor. We denote by
![]() $\mathcal {P}_A$
(resp.
$\mathcal {P}_A$
(resp.
![]() $(\mathcal {P}_0)_A$
) the base change of
$(\mathcal {P}_0)_A$
) the base change of
![]() $\mathcal {P}$
(resp.
$\mathcal {P}$
(resp.
![]() $\mathcal {P}_0$
) to A. Let
$\mathcal {P}_0$
) to A. Let
![]() $\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
be the extended G-shtuka over S with one leg at
$\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
be the extended G-shtuka over S with one leg at
![]() $S^\sharp $
associated with
$S^\sharp $
associated with
![]() $\mathcal {P}$
. A quasi-isogeny
$\mathcal {P}$
. A quasi-isogeny
from
![]() $\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
$\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
![]() $\mathcal {P}_0$
induces a quasi-isogeny
$\mathcal {P}_0$
induces a quasi-isogeny
![]() $ \eta _\iota \colon \mathcal {P}_A[1/\pi ] \overset {\sim }{\to } (\mathcal {P}_0)_A[1/\pi ] $
by base change along (5.1). The following proposition is implicitly proved in [Reference GleasonGle22a].
$ \eta _\iota \colon \mathcal {P}_A[1/\pi ] \overset {\sim }{\to } (\mathcal {P}_0)_A[1/\pi ] $
by base change along (5.1). The following proposition is implicitly proved in [Reference GleasonGle22a].
Proposition 5.2.6 [Reference GleasonGle22a].
The above construction
![]() $\iota \mapsto \eta _\iota $
induces a bijection between the set of quasi-isogenies
$\iota \mapsto \eta _\iota $
induces a bijection between the set of quasi-isogenies
![]() $\iota $
from
$\iota $
from
![]() $\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
$\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
![]() $\mathcal {P}_0$
such that
$\mathcal {P}_0$
such that
![]() $(\eta _\iota )_{ {\mathrm {red}} }$
is effective and the set of quasi-isogenies
$(\eta _\iota )_{ {\mathrm {red}} }$
is effective and the set of quasi-isogenies
![]() $\eta $
from
$\eta $
from
![]() $\mathcal {P}_A$
to
$\mathcal {P}_A$
to
![]() $(\mathcal {P}_0)_A$
such that
$(\mathcal {P}_0)_A$
such that
![]() $\eta _{ {\mathrm {red}} }$
is effective.
$\eta _{ {\mathrm {red}} }$
is effective.
Proof. We fix trivializations
![]() $\mathcal {P} \simeq G_{W_{{\mathcal O}_E}(R^+)}$
and
$\mathcal {P} \simeq G_{W_{{\mathcal O}_E}(R^+)}$
and
![]() $\mathcal {P}_0 \simeq G_{{\mathcal O}_{\breve {E}}}$
. We first prove the injectivity of the map. Let
$\mathcal {P}_0 \simeq G_{{\mathcal O}_{\breve {E}}}$
. We first prove the injectivity of the map. Let
![]() $\iota $
and
$\iota $
and
![]() $\iota '$
be quasi-isogenies from
$\iota '$
be quasi-isogenies from
![]() $\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
$\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
![]() $\mathcal {P}_0$
defined over
$\mathcal {P}_0$
defined over
![]() $\mathcal {Y}^{[n, \infty ]}_S$
such that
$\mathcal {Y}^{[n, \infty ]}_S$
such that
![]() $(\eta _\iota )_{ {\mathrm {red}} }$
and
$(\eta _\iota )_{ {\mathrm {red}} }$
and
![]() $(\eta _{\iota '})_{ {\mathrm {red}} }$
are effective. We assume that
$(\eta _{\iota '})_{ {\mathrm {red}} }$
are effective. We assume that
![]() $\eta _{\iota }=\eta _{\iota '}$
. We identify
$\eta _{\iota }=\eta _{\iota '}$
. We identify
![]() $\iota $
and
$\iota $
and
![]() $\iota '$
with elements
$\iota '$
with elements
![]() $g, g' \in G(B^{[n, \infty ]}_S)$
, respectively. Arguing as in [Reference GleasonGle22a, Lemma 2.14], we can find elements
$g, g' \in G(B^{[n, \infty ]}_S)$
, respectively. Arguing as in [Reference GleasonGle22a, Lemma 2.14], we can find elements
![]() $h, h' \in G(W_{{\mathcal O}_E}(R^+))$
such that for some
$h, h' \in G(W_{{\mathcal O}_E}(R^+))$
such that for some
![]() $r \geq n$
and
$r \geq n$
and
![]() $m \geq 1$
, we have
$m \geq 1$
, we have
![]() $h=g$
and
$h=g$
and
![]() $h'=g'$
in
$h'=g'$
in
![]() $G(B^{[r, \infty ]}_S/[\varpi ^\flat ]^{1/q^m})$
. Since
$G(B^{[r, \infty ]}_S/[\varpi ^\flat ]^{1/q^m})$
. Since
![]() $\eta _{\iota }=\eta _{\iota '}$
, we see that
$\eta _{\iota }=\eta _{\iota '}$
, we see that
![]() $h=h'$
in
$h=h'$
in
![]() $G(W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ]^{1/q^{m}})$
. This implies that
$G(W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ]^{1/q^{m}})$
. This implies that
![]() $g=g'$
in
$g=g'$
in
![]() $G(B^{[r, \infty ]}_S/[\varpi ^\flat ]^{1/q^{m}})$
. It now follows from [Reference GleasonGle22a, Lemma 2.15] (which also holds for general
$G(B^{[r, \infty ]}_S/[\varpi ^\flat ]^{1/q^{m}})$
. It now follows from [Reference GleasonGle22a, Lemma 2.15] (which also holds for general
![]() ${\mathcal O}_E$
) that
${\mathcal O}_E$
) that
![]() $g=g'$
in
$g=g'$
in
![]() $G(B^{[r, \infty ]}_S)$
, whence
$G(B^{[r, \infty ]}_S)$
, whence
![]() $\iota =\iota '$
.
$\iota =\iota '$
.
Let
![]() $\eta \colon \mathcal {P}_A[1/\pi ] \overset {\sim }{\to } (\mathcal {P}_0)_A[1/\pi ]$
be a quasi-isogeny such that
$\eta \colon \mathcal {P}_A[1/\pi ] \overset {\sim }{\to } (\mathcal {P}_0)_A[1/\pi ]$
be a quasi-isogeny such that
![]() $\eta _{ {\mathrm {red}} }$
is effective. By applying [Reference GleasonGle22a, Lemma 2.15] to the base change of
$\eta _{ {\mathrm {red}} }$
is effective. By applying [Reference GleasonGle22a, Lemma 2.15] to the base change of
![]() $\eta $
along
$\eta $
along
![]() $A[1/\pi ] \to B^{[n, \infty ]}_S/[\varpi ^\flat ]$
, we can find a quasi-isogeny
$A[1/\pi ] \to B^{[n, \infty ]}_S/[\varpi ^\flat ]$
, we can find a quasi-isogeny
![]() $\iota $
from
$\iota $
from
![]() $\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
$\widetilde {\mathcal {P}}_{ {\mathrm {sht}} }$
to
![]() $\mathcal {P}_0$
with
$\mathcal {P}_0$
with
![]() $\eta _\iota =\eta $
. This proves that the map is surjective.
$\eta _\iota =\eta $
. This proves that the map is surjective.
5.3 Formal completions of integral local Shimura varieties
Let
![]() $\mu \colon {\mathbb G}_m \to G_{{\mathcal O}_{\breve {E}}}$
be a minuscule cocharacter. Let
$\mu \colon {\mathbb G}_m \to G_{{\mathcal O}_{\breve {E}}}$
be a minuscule cocharacter. Let
![]() $B(G)$
be the set of
$B(G)$
be the set of
![]() $\phi $
-conjugacy classes of
$\phi $
-conjugacy classes of
![]() $G(\breve {E})$
and let
$G(\breve {E})$
and let
![]() $B(G, \mu ^{-1}) \subset B(G)$
be the subset of neutral acceptable elements for
$B(G, \mu ^{-1}) \subset B(G)$
be the subset of neutral acceptable elements for
![]() $\mu ^{-1}$
; see [Reference Pappas and RapoportPR24, Section 2.4.1]. Let
$\mu ^{-1}$
; see [Reference Pappas and RapoportPR24, Section 2.4.1]. Let
![]() $b \in G(\breve {E})$
be an element such that its
$b \in G(\breve {E})$
be an element such that its
![]() $\phi $
-conjugacy class belongs to
$\phi $
-conjugacy class belongs to
![]() $B(G, \mu ^{-1})$
. Let
$B(G, \mu ^{-1})$
. Let
![]() $\mathcal {E}_b=G_{{\mathcal O}_{\breve {E}}}$
be the G-Breuil–Kisin module over
$\mathcal {E}_b=G_{{\mathcal O}_{\breve {E}}}$
be the G-Breuil–Kisin module over
![]() $({\mathcal O}_{\breve {E}}, (\pi ))$
with the Frobenius given by
$({\mathcal O}_{\breve {E}}, (\pi ))$
with the Frobenius given by
![]() $g \mapsto bg$
.
$g \mapsto bg$
.
Definition 5.3.1 [Reference Scholze and WeinsteinSW20, Definition 25.1.1], [Reference Pappas and RapoportPR24, Definition 3.2.1].
The integral moduli space of local shtukas
associated with the triple
![]() $(G, b, \mu )$
is the v-sheaf on
$(G, b, \mu )$
is the v-sheaf on
![]() $ {\mathrm {Perf}} _k$
which sends an affinoid perfectoid space
$ {\mathrm {Perf}} _k$
which sends an affinoid perfectoid space
![]() $S= \mathrm {Spa}(R, R^+)$
over k to the set of isomorphism classes of tuples
$S= \mathrm {Spa}(R, R^+)$
over k to the set of isomorphism classes of tuples
consisting of an untilt
![]() $S^{\sharp }= \mathrm {Spa}(R^{\sharp }, R^{\sharp +})$
of S over
$S^{\sharp }= \mathrm {Spa}(R^{\sharp }, R^{\sharp +})$
of S over
![]() ${\mathcal O}_{\breve {E}}$
, a G-shtuka
${\mathcal O}_{\breve {E}}$
, a G-shtuka
![]() $\mathscr {P}$
over S with one leg at
$\mathscr {P}$
over S with one leg at
![]() $S^\sharp $
which is bounded by
$S^\sharp $
which is bounded by
![]() $\mu $
, and a quasi-isogeny
$\mu $
, and a quasi-isogeny
![]() $\iota $
from
$\iota $
from
![]() $\mathscr {P}$
to
$\mathscr {P}$
to
![]() $\mathcal {E}_b$
. We also call
$\mathcal {E}_b$
. We also call
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
the integral local Shimura variety (with hyperspecial level structure). To see that
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
the integral local Shimura variety (with hyperspecial level structure). To see that
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is a v-sheaf, we can use [Reference Scholze and WeinsteinSW20, Proposition 19.5.3]. (Although only the case of
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is a v-sheaf, we can use [Reference Scholze and WeinsteinSW20, Proposition 19.5.3]. (Although only the case of
![]() ${\mathcal O}_E={\mathbb Z}_p$
is considered in [Reference Scholze and WeinsteinSW20, Proposition 19.5.3], the same argument works for general
${\mathcal O}_E={\mathbb Z}_p$
is considered in [Reference Scholze and WeinsteinSW20, Proposition 19.5.3], the same argument works for general
![]() ${\mathcal O}_E$
.)
${\mathcal O}_E$
.)
We have a morphism
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu } \to {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
defined by
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu } \to {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
defined by
![]() $(S^{\sharp }, \mathscr {P}, \iota ) \mapsto S^{\sharp }$
. Namely,
$(S^{\sharp }, \mathscr {P}, \iota ) \mapsto S^{\sharp }$
. Namely,
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is a v-sheaf over
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is a v-sheaf over
![]() $ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
. The generic fiber of
$ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
. The generic fiber of
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is (the v-sheaf associated with) the local Shimura variety
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is (the v-sheaf associated with) the local Shimura variety
![]() $\mathcal {M}_{G_E, b, \mu , K}$
over
$\mathcal {M}_{G_E, b, \mu , K}$
over
![]() $ \mathrm {Spa} (\breve {E}, {\mathcal O}_{\breve {E}})$
, where
$ \mathrm {Spa} (\breve {E}, {\mathcal O}_{\breve {E}})$
, where
![]() $K:=G({\mathcal O}_E)$
.
$K:=G({\mathcal O}_E)$
.
Remark 5.3.2. Let
![]() $S= \mathrm {Spa}(R, R^+)$
be a product of points over k and let
$S= \mathrm {Spa}(R, R^+)$
be a product of points over k and let
![]() $(S^{\sharp }, \mathscr {P}, \iota ) \in \mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }(S)$
. By Remark 5.2.2, we can uniquely extend
$(S^{\sharp }, \mathscr {P}, \iota ) \in \mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }(S)$
. By Remark 5.2.2, we can uniquely extend
![]() $\mathscr {P}$
to an extended G-shtuka
$\mathscr {P}$
to an extended G-shtuka
![]() $\widetilde {\mathscr {P}}$
over S with one leg at
$\widetilde {\mathscr {P}}$
over S with one leg at
![]() $S^\sharp $
and regard
$S^\sharp $
and regard
![]() $\iota $
as a quasi-isogeny from
$\iota $
as a quasi-isogeny from
![]() $\widetilde {\mathscr {P}}$
to
$\widetilde {\mathscr {P}}$
to
![]() $\mathcal {E}_b$
. By Corollary 5.1.15, Proposition 5.1.10 and Proposition 2.4.5, there is a unique (up to isomorphism) G-
$\mathcal {E}_b$
. By Corollary 5.1.15, Proposition 5.1.10 and Proposition 2.4.5, there is a unique (up to isomorphism) G-
![]() $\mu ^{-1}$
-display
$\mu ^{-1}$
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
such that
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
such that
![]() $ \widetilde {(\mathcal {Q}_{\mathrm {BK}})}_{ {\mathrm {sht}} } \simeq \widetilde {\mathscr {P}}. $
We note
$ \widetilde {(\mathcal {Q}_{\mathrm {BK}})}_{ {\mathrm {sht}} } \simeq \widetilde {\mathscr {P}}. $
We note
![]() $\mathcal {Q}$
is banal by Proposition 2.5.3. (One can show that the Hodge filtration
$\mathcal {Q}$
is banal by Proposition 2.5.3. (One can show that the Hodge filtration
![]() $P(\mathcal {Q})_{R^{\sharp +}}$
is trivial as a
$P(\mathcal {Q})_{R^{\sharp +}}$
is trivial as a
![]() $P_\mu $
-torsor over
$P_\mu $
-torsor over
![]() $ \mathrm {Spec} R^{\sharp +}$
arguing as in the proof of [Reference ItoIto23, Proposition 5.6.11].) Let
$ \mathrm {Spec} R^{\sharp +}$
arguing as in the proof of [Reference ItoIto23, Proposition 5.6.11].) Let
![]() $\mathcal {Q}_{ {\mathrm {red}} }$
be the base change of
$\mathcal {Q}_{ {\mathrm {red}} }$
be the base change of
![]() $\mathcal {Q}$
along
$\mathcal {Q}$
along
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}}) \to (W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
. Then
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}}) \to (W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
. Then
![]() $\iota $
induces a quasi-isogeny
$\iota $
induces a quasi-isogeny
as in Proposition 5.2.6. Here, the base change of
![]() $\mathcal {E}_b$
to
$\mathcal {E}_b$
to
![]() $(W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
is denoted by the same symbol.
$(W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
is denoted by the same symbol.
Let
![]() $\mathcal {Q}_0$
be a G-
$\mathcal {Q}_0$
be a G-
![]() $\mu ^{-1}$
-display over
$\mu ^{-1}$
-display over
![]() $({\mathcal O}_{\breve {E}}, (\pi ))$
together with a quasi-isogeny
$({\mathcal O}_{\breve {E}}, (\pi ))$
together with a quasi-isogeny
We note that
![]() $\mathcal {Q}_0$
is banal by Proposition 2.5.3. In particular,
$\mathcal {Q}_0$
is banal by Proposition 2.5.3. In particular,
![]() $(\mathcal {Q}_0)_{\mathrm {BK}}$
is trivial as a G-torsor over
$(\mathcal {Q}_0)_{\mathrm {BK}}$
is trivial as a G-torsor over
![]() $ \mathrm {Spec} {\mathcal O}_{\breve {E}}$
. We fix a trivialization
$ \mathrm {Spec} {\mathcal O}_{\breve {E}}$
. We fix a trivialization
![]() $(\mathcal {Q}_0)_{\mathrm {BK}} \simeq G_{{\mathcal O}_{\breve {E}}}$
. Then
$(\mathcal {Q}_0)_{\mathrm {BK}} \simeq G_{{\mathcal O}_{\breve {E}}}$
. Then
![]() $\iota _0$
can be regarded as an element
$\iota _0$
can be regarded as an element
![]() $g \in G(\breve {E})$
such that
$g \in G(\breve {E})$
such that
![]() $g^{-1}b\phi (g) \in G({\mathcal O}_{\breve {E}})\mu (\pi )^{-1} G({\mathcal O}_{\breve {E}})$
. The image of g in
$g^{-1}b\phi (g) \in G({\mathcal O}_{\breve {E}})\mu (\pi )^{-1} G({\mathcal O}_{\breve {E}})$
. The image of g in
![]() $G(\breve {E})/G({\mathcal O}_{\breve {E}})$
does not depend on the choice of
$G(\breve {E})/G({\mathcal O}_{\breve {E}})$
does not depend on the choice of
![]() $(\mathcal {Q}_0)_{\mathrm {BK}} \simeq G_{{\mathcal O}_{\breve {E}}}$
. In this way, we obtain a point
$(\mathcal {Q}_0)_{\mathrm {BK}} \simeq G_{{\mathcal O}_{\breve {E}}}$
. In this way, we obtain a point
of the affine Deligne–Lusztig variety
![]() $X_{G}(b, \mu ^{-1})$
.
$X_{G}(b, \mu ^{-1})$
.
Definition 5.3.3 [Reference GleasonGle22b].
The formal completion
of
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
at x is the subsheaf of
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
at x is the subsheaf of
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
which sends a product of points
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
which sends a product of points
![]() $S= \mathrm {Spa}(R, R^+)$
over k to the set of isomorphism classes of tuples
$S= \mathrm {Spa}(R, R^+)$
over k to the set of isomorphism classes of tuples
![]() $ (S^{\sharp }, \mathscr {P}, \iota ) \in \mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }(S) $
such that, for the associated G-
$ (S^{\sharp }, \mathscr {P}, \iota ) \in \mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }(S) $
such that, for the associated G-
![]() $\mu ^{-1}$
-display
$\mu ^{-1}$
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
, there exists an isomorphism
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
, there exists an isomorphism
![]() $\mathcal {Q}_{ {\mathrm {red}} } \overset {\sim }{\to } \mathcal {Q}_{0}$
of G-
$\mathcal {Q}_{ {\mathrm {red}} } \overset {\sim }{\to } \mathcal {Q}_{0}$
of G-
![]() $\mu ^{-1}$
-displays over
$\mu ^{-1}$
-displays over
![]() $(W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
which makes the following diagram commute:
$(W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
which makes the following diagram commute:

See Remark 5.3.2 for the notation used here. As in Remark 5.3.2, the base change of
![]() $(\mathcal {Q}_{0})_{\mathrm {BK}}$
to
$(\mathcal {Q}_{0})_{\mathrm {BK}}$
to
![]() $(W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
is denoted by the same symbol.
$(W_{{\mathcal O}_E}(R^+_{ {\mathrm {red}} }), (\pi ))$
is denoted by the same symbol.
Remark 5.3.4. It is easy to see that the subsheaf
![]() $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
exists and is uniquely determined by the above condition (since products of points over k form a basis of
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
exists and is uniquely determined by the above condition (since products of points over k form a basis of
![]() $ {\mathrm {Perf}} _k$
with respect to the v-topology). In [Reference GleasonGle22b], Gleason gives a more conceptual definition of
$ {\mathrm {Perf}} _k$
with respect to the v-topology). In [Reference GleasonGle22b], Gleason gives a more conceptual definition of
![]() $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
. With the notation of [Reference GleasonGle22b],
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
. With the notation of [Reference GleasonGle22b],
![]() $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
is the formal neighborhood of
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
is the formal neighborhood of
![]() $x \in (\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu })^{\mathrm {red}}$
on the prekimberlite
$x \in (\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu })^{\mathrm {red}}$
on the prekimberlite
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
; see [Reference GleasonGle22b, Definition 4.18]. We note that
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
; see [Reference GleasonGle22b, Definition 4.18]. We note that
![]() $(\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu })^{\mathrm {red}}$
can be identified with the affine Deligne–Lusztig variety
$(\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu })^{\mathrm {red}}$
can be identified with the affine Deligne–Lusztig variety
![]() $X_{G}(b, \mu ^{-1})$
by [Reference GleasonGle22a, Proposition 2.30]. See also [Reference GleasonGle22a, Lemma 2.31] for the fact that
$X_{G}(b, \mu ^{-1})$
by [Reference GleasonGle22a, Proposition 2.30]. See also [Reference GleasonGle22a, Lemma 2.31] for the fact that
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is a prekimberlite (in the sense of [Reference GleasonGle22b, Definition 4.15]).
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
is a prekimberlite (in the sense of [Reference GleasonGle22b, Definition 4.15]).
We consider the local ring
![]() $R_{G, \mu ^{-1}}$
over
$R_{G, \mu ^{-1}}$
over
![]() ${\mathcal O}_{\breve {E}}$
defined as in Definition 3.4.3. There is an isomorphism
${\mathcal O}_{\breve {E}}$
defined as in Definition 3.4.3. There is an isomorphism
![]() $ R_{G, \mu ^{-1}} \simeq {\mathcal O}_{\breve {E}}[[t_1, \dotsc , t_r]] $
over
$ R_{G, \mu ^{-1}} \simeq {\mathcal O}_{\breve {E}}[[t_1, \dotsc , t_r]] $
over
![]() ${\mathcal O}_{\breve {E}}$
. We endow
${\mathcal O}_{\breve {E}}$
. We endow
![]() $R_{G, \mu ^{-1}}$
with the
$R_{G, \mu ^{-1}}$
with the
![]() $\mathfrak {m}_{G, \mu ^{-1}}$
-adic topology. Let
$\mathfrak {m}_{G, \mu ^{-1}}$
-adic topology. Let
![]() $ {\mathrm {Spd}} R_{G, \mu ^{-1}} $
be the v-sheaf (over
$ {\mathrm {Spd}} R_{G, \mu ^{-1}} $
be the v-sheaf (over
![]() $ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
) on
$ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
) on
![]() $ {\mathrm {Perf}} _k$
which sends a perfectoid space S over k to the set of isomorphism classes of untilts
$ {\mathrm {Perf}} _k$
which sends a perfectoid space S over k to the set of isomorphism classes of untilts
![]() $S^\sharp $
of S over
$S^\sharp $
of S over
![]() ${\mathcal O}_{\breve {E}}$
equipped with a morphism of adic spaces
${\mathcal O}_{\breve {E}}$
equipped with a morphism of adic spaces
![]() $S^\sharp \to \mathrm {Spa} R_{G, \mu ^{-1}}$
over
$S^\sharp \to \mathrm {Spa} R_{G, \mu ^{-1}}$
over
![]() ${\mathcal O}_{\breve {E}}$
; see [Reference Scholze and WeinsteinSW20, Section 18.4].
${\mathcal O}_{\breve {E}}$
; see [Reference Scholze and WeinsteinSW20, Section 18.4].
The main result of this section is the following theorem.
Theorem 5.3.5. There exists an isomorphism
of v-sheaves over
![]() $ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
.
$ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
.
Proof. Let
![]() $S= \mathrm {Spa}(R, R^+)$
be a product of points over k and let
$S= \mathrm {Spa}(R, R^+)$
be a product of points over k and let
![]() $S^{\sharp }= \mathrm {Spa}(R^{\sharp }, R^{\sharp +})$
be an untilt of S over
$S^{\sharp }= \mathrm {Spa}(R^{\sharp }, R^{\sharp +})$
be an untilt of S over
![]() ${\mathcal O}_{\breve {E}}$
. Then the inverse image of
${\mathcal O}_{\breve {E}}$
. Then the inverse image of
![]() $S^{\sharp } \in ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
under the map
$S^{\sharp } \in ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
under the map
![]() $( {\mathrm {Spd}} R_{G, \mu ^{-1}})(S) \to ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
can be identified with the set of continuous homomorphisms
$( {\mathrm {Spd}} R_{G, \mu ^{-1}})(S) \to ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
can be identified with the set of continuous homomorphisms
![]() $R_{G, \mu ^{-1}} \to R^{\sharp +}$
over
$R_{G, \mu ^{-1}} \to R^{\sharp +}$
over
![]() ${\mathcal O}_{\breve {E}}$
.
${\mathcal O}_{\breve {E}}$
.
Let
![]() $\varpi ^{\flat } \in R^+$
be a pseudo-uniformizer such that
$\varpi ^{\flat } \in R^+$
be a pseudo-uniformizer such that
![]() $\pi \in (\varpi )$
in
$\pi \in (\varpi )$
in
![]() $R^{\sharp +}$
, where
$R^{\sharp +}$
, where
![]() $\varpi :=\theta ([\varpi ^\flat ]) \in R^{\sharp +}$
. The inverse image of
$\varpi :=\theta ([\varpi ^\flat ]) \in R^{\sharp +}$
. The inverse image of
![]() $S^{\sharp } \in ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
under the map
$S^{\sharp } \in ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
under the map
![]() $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}(S) \to ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
can be identified with the set of isomorphism classes of pairs
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}(S) \to ( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
can be identified with the set of isomorphism classes of pairs
![]() $ (\mathcal {Q}, \eta ) $
consisting of a banal G-
$ (\mathcal {Q}, \eta ) $
consisting of a banal G-
![]() $\mu ^{-1}$
-display
$\mu ^{-1}$
-display
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
and an element
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
and an element
![]() $\eta $
of the set
$\eta $
of the set
where
![]() $(A_m, (\pi ))=(W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ]^{1/q^m}, (\pi ))$
, and
$(A_m, (\pi ))=(W_{{\mathcal O}_E}(R^+)/[\varpi ^\flat ]^{1/q^m}, (\pi ))$
, and
![]() $\mathcal {Q}_m$
(resp.
$\mathcal {Q}_m$
(resp.
![]() $(\mathcal {Q}_0)_m$
) is the base change of
$(\mathcal {Q}_0)_m$
) is the base change of
![]() $\mathcal {Q}$
(resp.
$\mathcal {Q}$
(resp.
![]() $\mathcal {Q}_0$
) to
$\mathcal {Q}_0$
) to
![]() $(A_m, (\pi ))$
. This follows by combining Proposition 2.4.5, Proposition 5.1.10, Corollary 5.1.15, Lemma 5.2.4, Lemma 5.2.5 and Proposition 5.2.6.
$(A_m, (\pi ))$
. This follows by combining Proposition 2.4.5, Proposition 5.1.10, Corollary 5.1.15, Lemma 5.2.4, Lemma 5.2.5 and Proposition 5.2.6.
By Theorem 4.1.7, there exists a universal deformation
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
of
$\mathfrak {Q}^{ {\mathrm {univ}} }$
of
![]() $\mathcal {Q}_0$
over
$\mathcal {Q}_0$
over
![]() $R_{G, \mu ^{-1}}$
. Moreover,
$R_{G, \mu ^{-1}}$
. Moreover,
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
has the property
$\mathfrak {Q}^{ {\mathrm {univ}} }$
has the property
![]() $(\mathrm {Perfd})$
. Let
$(\mathrm {Perfd})$
. Let
![]() $g \colon R_{G, \mu ^{-1}} \to R^{\sharp +}$
be a continuous homomorphism over
$g \colon R_{G, \mu ^{-1}} \to R^{\sharp +}$
be a continuous homomorphism over
![]() ${\mathcal O}_{\breve {E}}$
. We regard
${\mathcal O}_{\breve {E}}$
. We regard
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
as an object of
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
as an object of ![]() via the homomorphism g, and let
via the homomorphism g, and let
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }_g$
be the associated G-
$\mathfrak {Q}^{ {\mathrm {univ}} }_g$
be the associated G-
![]() $\mu ^{-1}$
-display over
$\mu ^{-1}$
-display over
![]() $(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
. For some
$(W_{{\mathcal O}_E}(R^+), I_{R^{\sharp +}})$
. For some
![]() $m \geq 1$
, we have
$m \geq 1$
, we have
![]() $g(\mathfrak {m}_{G, \mu ^{-1}}) \subset (\varpi ^{1/q^m})$
in
$g(\mathfrak {m}_{G, \mu ^{-1}}) \subset (\varpi ^{1/q^m})$
in
![]() $R^{\sharp +}$
, where
$R^{\sharp +}$
, where
![]() $\varpi ^{1/q^m}:=\theta ([\varpi ^\flat ]^{1/q^m}) \in R^{\sharp +}$
. Hence, there is a natural isomorphism
$\varpi ^{1/q^m}:=\theta ([\varpi ^\flat ]^{1/q^m}) \in R^{\sharp +}$
. Hence, there is a natural isomorphism
![]() $ \eta _g \colon (\mathfrak {Q}^{ {\mathrm {univ}} }_g)_m \overset {\sim }{\to } (\mathcal {Q}_0)_m $
over
$ \eta _g \colon (\mathfrak {Q}^{ {\mathrm {univ}} }_g)_m \overset {\sim }{\to } (\mathcal {Q}_0)_m $
over
![]() $(A_m, (\pi ))$
. We define a map
$(A_m, (\pi ))$
. We define a map
by
![]() $g \mapsto (\mathfrak {Q}^{ {\mathrm {univ}} }_g, \eta _g)$
. Using the property
$g \mapsto (\mathfrak {Q}^{ {\mathrm {univ}} }_g, \eta _g)$
. Using the property
![]() $(\mathrm {Perfd})$
and using Proposition 3.1.5, we see that this map is bijective. Then we obtain a bijection
$(\mathrm {Perfd})$
and using Proposition 3.1.5, we see that this map is bijective. Then we obtain a bijection
![]() $ ( {\mathrm {Spd}} R_{G, \mu ^{-1}})(S) \overset {\sim }{\to } \widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}(S) $
over
$ ( {\mathrm {Spd}} R_{G, \mu ^{-1}})(S) \overset {\sim }{\to } \widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}(S) $
over
![]() $( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
, which is independent of the choice of
$( {\mathrm {Spd}} {\mathcal O}_{\breve {E}})(S)$
, which is independent of the choice of
![]() $\varpi ^\flat $
and is functorial in S. Since products of points over k form a basis of
$\varpi ^\flat $
and is functorial in S. Since products of points over k form a basis of
![]() $ {\mathrm {Perf}} _k$
, we finally get the desired isomorphism
$ {\mathrm {Perf}} _k$
, we finally get the desired isomorphism
![]() $ {\mathrm {Spd}} R_{G, \mu ^{-1}} \overset {\sim }{\to } \widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x} $
of v-sheaves over
$ {\mathrm {Spd}} R_{G, \mu ^{-1}} \overset {\sim }{\to } \widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x} $
of v-sheaves over
![]() $ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
.
$ {\mathrm {Spd}} {\mathcal O}_{\breve {E}}$
.
In the following, we assume that
![]() ${\mathcal O}_E={\mathbb Z}_p$
for simplicity.
${\mathcal O}_E={\mathbb Z}_p$
for simplicity.
Remark 5.3.6. Theorem 5.3.5 implies that a conjecture of Pappas–Rapoport [Reference Pappas and RapoportPR24, Conjecture 3.3.5] in the hyperspecial case, which was originally proposed by Gleason [Reference GleasonGle21, Conjecture 1], holds true. This result was already known in the following cases.
-
(1) In [Reference Pappas and RapoportPR22], Pappas–Rapoport proved Theorem 5.3.5 under the assumption that
 $p \geq 3$
and the pair
$p \geq 3$
and the pair
 $(G_{{\mathbb Q}_p}, \mu )$
is of abelian type in the sense of [Reference Pappas and RapoportPR22, Definition 2.1.3]. In fact, the result is formulated and proved in the more general case where G is parahoric. If
$(G_{{\mathbb Q}_p}, \mu )$
is of abelian type in the sense of [Reference Pappas and RapoportPR22, Definition 2.1.3]. In fact, the result is formulated and proved in the more general case where G is parahoric. If
 $p=2$
, the same result is obtained under the additional assumption that
$p=2$
, the same result is obtained under the additional assumption that
 $G_{{\mathbb Q}_p}$
is of type A or C.
$G_{{\mathbb Q}_p}$
is of type A or C. -
(2) In [Reference BartlingBar22], Bartling proved Theorem 5.3.5 under the assumption that the element b satisfies the adjoint nilpotent condition introduced in [Reference Bültel and PappasBP20, Definition 3.4.2] and
 $p \geq 3$
. He studied the relation between
$p \geq 3$
. He studied the relation between
 $\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
and the deformation space constructed by Bültel–Pappas [Reference Bültel and PappasBP20, 3.5.9].
$\widehat {\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }}_{/ x}$
and the deformation space constructed by Bültel–Pappas [Reference Bültel and PappasBP20, 3.5.9].
Remark 5.3.7. Scholze conjectured that there exists a (unique) normal formal scheme
![]() $\mathscr {M}_{G, b, \mu }$
which is flat and locally formally of finite type over
$\mathscr {M}_{G, b, \mu }$
which is flat and locally formally of finite type over
![]() $ \mathrm {Spf} W(k)$
such that the v-sheaf associated with
$ \mathrm {Spf} W(k)$
such that the v-sheaf associated with
![]() $\mathscr {M}_{G, b, \mu }$
is isomorphic to
$\mathscr {M}_{G, b, \mu }$
is isomorphic to
![]() $\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
. (This conjecture is stated in the more general case where G is parahoric.) If
$\mathcal {M}^{{ {\mathrm {int}} }}_{G, b, \mu }$
. (This conjecture is stated in the more general case where G is parahoric.) If
![]() $(G, b, \mu )$
is of EL type or PEL type, then this is proved in [Reference Scholze and WeinsteinSW20, Lecture 25]. Moreover, in the case (1) of Remark 5.3.6, this is proved in [Reference Pappas and RapoportPR22] using Theorem 5.3.5. Since we have proved Theorem 5.3.5 for any p (including
$(G, b, \mu )$
is of EL type or PEL type, then this is proved in [Reference Scholze and WeinsteinSW20, Lecture 25]. Moreover, in the case (1) of Remark 5.3.6, this is proved in [Reference Pappas and RapoportPR22] using Theorem 5.3.5. Since we have proved Theorem 5.3.5 for any p (including
![]() $p=2$
), we can prove that if
$p=2$
), we can prove that if
![]() $(G_{{\mathbb Q}_p}, \mu )$
is of abelian type, then
$(G_{{\mathbb Q}_p}, \mu )$
is of abelian type, then
![]() $\mathscr {M}_{G, b, \mu }$
exists for any p in the same way as in [Reference Pappas and RapoportPR22].
$\mathscr {M}_{G, b, \mu }$
exists for any p in the same way as in [Reference Pappas and RapoportPR22].
If
![]() $\mathscr {M}_{G, b, \mu }$
exists, then it is formally smooth over
$\mathscr {M}_{G, b, \mu }$
exists, then it is formally smooth over
![]() $ \mathrm {Spf} W(k)$
by Theorem 5.3.5.
$ \mathrm {Spf} W(k)$
by Theorem 5.3.5.
6 Comparison with universal deformations of p-divisible groups
In this section, we assume that
![]() ${\mathcal O}_E={\mathbb Z}_p$
. Let k be a perfect field of characteristic p. Let
${\mathcal O}_E={\mathbb Z}_p$
. Let k be a perfect field of characteristic p. Let
![]() $\mathcal {G}$
be a p-divisible group over
$\mathcal {G}$
be a p-divisible group over
![]() $ \mathrm {Spec} k$
of height N and of dimension d. Let
$ \mathrm {Spec} k$
of height N and of dimension d. Let
![]() $\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _N$
be the cocharacter over
$\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _N$
be the cocharacter over
![]() $W(k)$
defined by
$W(k)$
defined by
 $$\begin{align*}t \mapsto {\mathrm{diag}}{(\underbrace{t, \dotsc, t}_{N-d}, \underbrace{1, \dotsc, 1}_{d})}. \end{align*}$$
$$\begin{align*}t \mapsto {\mathrm{diag}}{(\underbrace{t, \dotsc, t}_{N-d}, \underbrace{1, \dotsc, 1}_{d})}. \end{align*}$$
Let
![]() $\mathcal {Q}$
be the
$\mathcal {Q}$
be the
![]() $ {\mathrm {GL}} _N$
-
$ {\mathrm {GL}} _N$
-
![]() $\mu $
-display over the prism
$\mu $
-display over the prism
![]() $(W(k), (p))$
associated with the Dieudonné module of
$(W(k), (p))$
associated with the Dieudonné module of
![]() $\mathcal {G}$
. For a universal deformation
$\mathcal {G}$
. For a universal deformation
![]() $\mathcal {G}^{ {\mathrm {univ}} }$
of
$\mathcal {G}^{ {\mathrm {univ}} }$
of
![]() $\mathcal {G}$
, we prove that the prismatic Dieudonné crystal of
$\mathcal {G}$
, we prove that the prismatic Dieudonné crystal of
![]() $\mathcal {G}^{ {\mathrm {univ}} }$
, as introduced in [Reference Anschütz and Le BrasALB23], induces a universal deformation
$\mathcal {G}^{ {\mathrm {univ}} }$
, as introduced in [Reference Anschütz and Le BrasALB23], induces a universal deformation
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
of
$\mathfrak {Q}^{ {\mathrm {univ}} }$
of
![]() $\mathcal {Q}$
; see Theorem 6.2.1. Then, by relating the properties
$\mathcal {Q}$
; see Theorem 6.2.1. Then, by relating the properties
![]() $\mathrm {(Perfd)}$
and
$\mathrm {(Perfd)}$
and
![]() $\mathrm {(BK)}$
of the universal deformation
$\mathrm {(BK)}$
of the universal deformation
![]() $\mathfrak {Q}^{ {\mathrm {univ}} }$
to the universal property of
$\mathfrak {Q}^{ {\mathrm {univ}} }$
to the universal property of
![]() $\mathcal {G}^{ {\mathrm {univ}} }$
, we establish some classification results of p-divisible groups; see Section 6.3 for details.
$\mathcal {G}^{ {\mathrm {univ}} }$
, we establish some classification results of p-divisible groups; see Section 6.3 for details.
6.1 Prismatic Dieudonné crystals of p-divisible groups
In this section and Section 7 below, we need the notion of quasisyntomic rings introduced in [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.10]. We refer to [Reference Bhatt, Morrow and ScholzeBMS19, Section 4] for basic properties of quasisyntomic rings.
Example 6.1.1.
-
(1) Let
 $R \in \mathcal {C}_{W(k)}$
be a complete regular local ring over
$R \in \mathcal {C}_{W(k)}$
be a complete regular local ring over
 $W(k)$
with residue field k. Then R is a quasisyntomic ring. Moreover,
$W(k)$
with residue field k. Then R is a quasisyntomic ring. Moreover,
 $R/\mathfrak {m}^m_R$
is a quasisyntomic ring if
$R/\mathfrak {m}^m_R$
is a quasisyntomic ring if
 $\dim R \leq 1$
. See [Reference Anschütz and Le BrasALB23, Example 3.17].
$\dim R \leq 1$
. See [Reference Anschütz and Le BrasALB23, Example 3.17]. -
(2) Let
 $(S, a^\flat )$
be a perfectoid pair (Definition 2.1.4). Then S and
$(S, a^\flat )$
be a perfectoid pair (Definition 2.1.4). Then S and
 $S/a^m$
are quasisyntomic rings. More precisely, S and
$S/a^m$
are quasisyntomic rings. More precisely, S and
 $S/a^m$
are quasiregular semiperfectoid rings in the sense of [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.20]; see [Reference Anschütz and Le BrasALB23, Example 3.20].
$S/a^m$
are quasiregular semiperfectoid rings in the sense of [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.20]; see [Reference Anschütz and Le BrasALB23, Example 3.20].
Let R be a p-adically complete ring. Let
![]() $\mathscr {G}$
be a p-divisible group over
$\mathscr {G}$
be a p-divisible group over
![]() $ \mathrm {Spec} R$
. Following [Reference Anschütz and Le BrasALB23], we consider the sheaf
$ \mathrm {Spec} R$
. Following [Reference Anschütz and Le BrasALB23], we consider the sheaf
on the site ![]() , where
, where
![]() $\underline {\mathscr {G}}$
is the sheaf defined by
$\underline {\mathscr {G}}$
is the sheaf defined by
![]() $(A, I) \mapsto \mathscr {G}(A/I)$
and
$(A, I) \mapsto \mathscr {G}(A/I)$
and ![]() is defined by
is defined by
![]() $(A, I) \mapsto A$
. In [Reference Anschütz and Le BrasALB23, Proposition 4.69], it is proved that
$(A, I) \mapsto A$
. In [Reference Anschütz and Le BrasALB23, Proposition 4.69], it is proved that ![]() is a finite projective A-module for any
is a finite projective A-module for any ![]() and its formation commutes with base change along any morphism
and its formation commutes with base change along any morphism
![]() $(A, I) \to (A', I')$
in
$(A, I) \to (A', I')$
in ![]() . By [Reference ItoIto23, Remark 7.3.1], there is a canonical isomorphism
. By [Reference ItoIto23, Remark 7.3.1], there is a canonical isomorphism
for any ![]() , where we view the site
, where we view the site ![]() as the localization of
as the localization of ![]() at
at
![]() $(A, I)$
, and the restriction of
$(A, I)$
, and the restriction of
![]() $\underline {\mathscr {G}}$
to
$\underline {\mathscr {G}}$
to ![]() is denoted by the same symbol. We set
is denoted by the same symbol. We set
In [Reference Anschütz and Le BrasALB23, Theorem 4.71], it is proved that if R is a quasisyntomic ring, then ![]() is a prismatic Dieudonné crystal on
is a prismatic Dieudonné crystal on ![]() in the sense that for any
in the sense that for any ![]() , the A-module
, the A-module ![]() with the A-linear homomorphism
with the A-linear homomorphism
induced by the Frobenius ![]() is a minuscule Breuil–Kisin module over
is a minuscule Breuil–Kisin module over
![]() $(A, I)$
, and its formation commutes with base change along any morphism
$(A, I)$
, and its formation commutes with base change along any morphism
![]() $(A, I) \to (A', I')$
in
$(A, I) \to (A', I')$
in ![]() . (See also [Reference ItoIto23, Section 7.3].)
. (See also [Reference ItoIto23, Section 7.3].)
Remark 6.1.2. We assume that R is a quasisyntomic ring. By [Reference Anschütz and Le BrasALB23, Proposition 4.4] (see also [Reference Bhatt and ScholzeBS23, Proposition 2.7]), the category of prismatic Dieudonné crystals on ![]() is equivalent to that of prismatic Dieudonné crystals over R in the sense of [Reference Anschütz and Le BrasALB23, Definition 4.5], which are defined as sheaves on the quasisyntomic site of R. Let
is equivalent to that of prismatic Dieudonné crystals over R in the sense of [Reference Anschütz and Le BrasALB23, Definition 4.5], which are defined as sheaves on the quasisyntomic site of R. Let
![]() $\mathrm {DM}(R)$
denote the category of prismatic Dieudonné crystals on
$\mathrm {DM}(R)$
denote the category of prismatic Dieudonné crystals on ![]() . We have an identification
. We have an identification
where
![]() $ \mathrm {BK}_{\mathrm {min}}(A, I) $
is the category of minuscule Breuil–Kisin modules over
$ \mathrm {BK}_{\mathrm {min}}(A, I) $
is the category of minuscule Breuil–Kisin modules over
![]() $(A, I)$
.
$(A, I)$
.
Example 6.1.3. Let
![]() $\mathfrak {S}:=W(k)[[t_1, \dotsc , t_n]]$
and
$\mathfrak {S}:=W(k)[[t_1, \dotsc , t_n]]$
and
![]() $ \mathfrak {S}_m:=W(k)[[t_1, \dotsc , t_n]]/(t_1, \dotsc , t_n)^{m} $
. We assume that
$ \mathfrak {S}_m:=W(k)[[t_1, \dotsc , t_n]]/(t_1, \dotsc , t_n)^{m} $
. We assume that
![]() $n \leq 1$
(so that
$n \leq 1$
(so that
![]() $\mathfrak {S}_m/p$
is a quasisyntomic ring by Example 6.1.1). Let
$\mathfrak {S}_m/p$
is a quasisyntomic ring by Example 6.1.1). Let
![]() $\mathscr {G}$
be a p-divisible group over
$\mathscr {G}$
be a p-divisible group over
![]() $ \mathrm {Spec} \mathfrak {S}_m/p$
. Then there exists a natural isomorphism
$ \mathrm {Spec} \mathfrak {S}_m/p$
. Then there exists a natural isomorphism
of minuscule Breuil–Kisin modules over
![]() $(\mathfrak {S}_m, (p))$
, where
$(\mathfrak {S}_m, (p))$
, where
![]() $\mathbb {D}(\mathscr {G})(\mathfrak {S}_m \to \mathfrak {S}_m/p)$
is the evaluation on the divided power extension
$\mathbb {D}(\mathscr {G})(\mathfrak {S}_m \to \mathfrak {S}_m/p)$
is the evaluation on the divided power extension
![]() $\mathfrak {S}_m \to \mathfrak {S}_m/p$
of the contravariant Dieudonné crystal
$\mathfrak {S}_m \to \mathfrak {S}_m/p$
of the contravariant Dieudonné crystal
![]() $\mathbb {D}(\mathscr {G})$
defined in [Reference Berthelot, Breen and MessingBBM82, Définition 3.3.6]. This is a special case of [Reference Anschütz and Le BrasALB23, Lemma 4.45].
$\mathbb {D}(\mathscr {G})$
defined in [Reference Berthelot, Breen and MessingBBM82, Définition 3.3.6]. This is a special case of [Reference Anschütz and Le BrasALB23, Lemma 4.45].
6.2 Universal deformations of p-divisible groups
Let
![]() $\mathcal {G}$
be a p-divisible group over
$\mathcal {G}$
be a p-divisible group over
![]() $ \mathrm {Spec} k$
. Let N be the height of
$ \mathrm {Spec} k$
. Let N be the height of
![]() $\mathcal {G}$
and let d be the dimension of
$\mathcal {G}$
and let d be the dimension of
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Let
![]() $ {\mathrm {Art}} _{W(k)}$
be the category of artinian local rings R with a local homomorphism
$ {\mathrm {Art}} _{W(k)}$
be the category of artinian local rings R with a local homomorphism
![]() $W(k) \to R$
which induces an isomorphism on the residue fields. By [Reference IllusieIll85, Corollaire 4.8] (or [Reference LauLau14, Proposition 3.11]), the functor
$W(k) \to R$
which induces an isomorphism on the residue fields. By [Reference IllusieIll85, Corollaire 4.8] (or [Reference LauLau14, Proposition 3.11]), the functor
![]() $ {\mathrm {Art}} _{W(k)} \to \mathrm {Set}$
sending R to the set of isomorphism classes of deformations of
$ {\mathrm {Art}} _{W(k)} \to \mathrm {Set}$
sending R to the set of isomorphism classes of deformations of
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} R$
is pro-representable by
$ \mathrm {Spec} R$
is pro-representable by
Let
![]() $\mathcal {G}^{ {\mathrm {univ}} }$
be a universal deformation of
$\mathcal {G}^{ {\mathrm {univ}} }$
be a universal deformation of
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} R^{ {\mathrm {univ}} }$
.
$ \mathrm {Spec} R^{ {\mathrm {univ}} }$
.
Let
![]() $\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _N$
be the cocharacter over
$\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _N$
be the cocharacter over
![]() $W(k)$
defined as in the beginning of this section. The minuscule Breuil–Kisin module
$W(k)$
defined as in the beginning of this section. The minuscule Breuil–Kisin module ![]() is of type
is of type
![]() $\mu $
for every
$\mu $
for every ![]() . Via the equivalence
. Via the equivalence ![]() in Example 2.4.7, the prismatic Dieudonné crystal
in Example 2.4.7, the prismatic Dieudonné crystal ![]() induces a prismatic
induces a prismatic
![]() $ {\mathrm {GL}} _N$
-
$ {\mathrm {GL}} _N$
-
![]() $\mu $
-display
$\mu $
-display
![]() $ \mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }) $
over
$ \mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }) $
over
![]() $R^{ {\mathrm {univ}} }$
. We set
$R^{ {\mathrm {univ}} }$
. We set
![]() $\mathcal {Q}:=\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} })_{(W(k), (p))}$
, which corresponds to
$\mathcal {Q}:=\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} })_{(W(k), (p))}$
, which corresponds to ![]() .
.
Theorem 6.2.1. The prismatic
![]() $ {\mathrm {GL}} _N$
-
$ {\mathrm {GL}} _N$
-
![]() $\mu $
-display
$\mu $
-display
![]() $ \mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }) $
over
$ \mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }) $
over
![]() $R^{ {\mathrm {univ}} }$
is a universal deformation of
$R^{ {\mathrm {univ}} }$
is a universal deformation of
![]() $\mathcal {Q}$
. Moreover,
$\mathcal {Q}$
. Moreover,
![]() $ \mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }) $
has the properties
$ \mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }) $
has the properties
![]() $\mathrm {(Perfd)}$
and
$\mathrm {(Perfd)}$
and
![]() $\mathrm {(BK)}$
.
$\mathrm {(BK)}$
.
Proof. Since
![]() $R_{ {\mathrm {GL}} _N, \mu } \simeq R^{ {\mathrm {univ}} }$
, it suffices to prove that
$R_{ {\mathrm {GL}} _N, \mu } \simeq R^{ {\mathrm {univ}} }$
, it suffices to prove that
![]() $\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} })$
is versal by Theorem 4.1.8. We consider the period map
$\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} })$
is versal by Theorem 4.1.8. We consider the period map
where
![]() $s^*\mathcal {Q}$
is the base change of
$s^*\mathcal {Q}$
is the base change of
![]() $\mathcal {Q}$
along the natural map
$\mathcal {Q}$
along the natural map
The period map
![]() $ {\mathrm {Per}} _{s^*\mathcal {Q}}$
is bijective by Theorem 3.3.4. Let
$ {\mathrm {Per}} _{s^*\mathcal {Q}}$
is bijective by Theorem 3.3.4. Let
![]() $ {\mathrm {Def}} (\mathcal {G})_{k[[t]]/t^2}$
be the set of isomorphism classes of deformations of
$ {\mathrm {Def}} (\mathcal {G})_{k[[t]]/t^2}$
be the set of isomorphism classes of deformations of
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm { Spec} k[[t]]/t^2$
. By the universal property of
$ \mathrm { Spec} k[[t]]/t^2$
. By the universal property of
![]() $\mathcal {G}^{ {\mathrm {univ}} }$
, we may identify
$\mathcal {G}^{ {\mathrm {univ}} }$
, we may identify
![]() $ {\mathrm {Def}} (\mathcal {G})_{k[[t]]/t^2}$
with
$ {\mathrm {Def}} (\mathcal {G})_{k[[t]]/t^2}$
with
![]() $\mathfrak {t}_{R^{ {\mathrm {univ}} }}$
. It thus suffices to show that the following composition is bijective:
$\mathfrak {t}_{R^{ {\mathrm {univ}} }}$
. It thus suffices to show that the following composition is bijective:
Let
![]() $\mathscr {G} \in {\mathrm {Def}} (\mathcal {G})_{k[[t]]/t^2}$
. By Example 6.1.3, we have
$\mathscr {G} \in {\mathrm {Def}} (\mathcal {G})_{k[[t]]/t^2}$
. By Example 6.1.3, we have
and
It follows from Example 2.5.5 and Proposition 3.2.7 that there exists a unique Frobenius equivariant isomorphism
which is a lift of the identity of
![]() $\mathbb {D}(\mathcal {G})(W(k))$
. We shall give a different description of
$\mathbb {D}(\mathcal {G})(W(k))$
. We shall give a different description of
![]() $\psi $
. The kernel of
$\psi $
. The kernel of
![]() $W(k)[[t]]/t^2 \to k$
has a unique divided power structure which is compatible with the usual divided power structure on
$W(k)[[t]]/t^2 \to k$
has a unique divided power structure which is compatible with the usual divided power structure on
![]() $(p)$
and the trivial divided power structure on
$(p)$
and the trivial divided power structure on
![]() $(t)$
. Then we have a chain of canonical isomorphisms
$(t)$
. Then we have a chain of canonical isomorphisms
 $$ \begin{align*} \mathbb{D}(\mathscr{G})(W(k)[[t]]/t^2 \to k[[t]]/t^2) &\simeq \mathbb{D}(\mathscr{G})(W(k)[[t]]/t^2 \to k) \\ & \simeq \mathbb{D}(\mathcal{G})(W(k)[[t]]/t^2 \to k) \\ & \simeq \mathbb{D}(\mathcal{G})(W(k)) \otimes_{W(k)} W(k)[[t]]/t^2, \end{align*} $$
$$ \begin{align*} \mathbb{D}(\mathscr{G})(W(k)[[t]]/t^2 \to k[[t]]/t^2) &\simeq \mathbb{D}(\mathscr{G})(W(k)[[t]]/t^2 \to k) \\ & \simeq \mathbb{D}(\mathcal{G})(W(k)[[t]]/t^2 \to k) \\ & \simeq \mathbb{D}(\mathcal{G})(W(k)) \otimes_{W(k)} W(k)[[t]]/t^2, \end{align*} $$
where the first and third isomorphisms are induced by the crystals
![]() $\mathbb {D}(\mathscr {G})$
and
$\mathbb {D}(\mathscr {G})$
and
![]() $\mathbb {D}(\mathcal {G})$
and the second one is induced by base change. The composition, denoted by
$\mathbb {D}(\mathcal {G})$
and the second one is induced by base change. The composition, denoted by
![]() $\psi '$
, is Frobenius equivariant and is a lift of the identity of
$\psi '$
, is Frobenius equivariant and is a lift of the identity of
![]() $\mathbb {D}(\mathcal {G})(W(k))$
. Then the uniqueness part of Proposition 3.2.7 ensures that
$\mathbb {D}(\mathcal {G})(W(k))$
. Then the uniqueness part of Proposition 3.2.7 ensures that
![]() $\psi =\psi '$
. In particular, we see that the reduction modulo p of
$\psi =\psi '$
. In particular, we see that the reduction modulo p of
![]() $\psi $
coincides with the composition of canonical isomorphisms
$\psi $
coincides with the composition of canonical isomorphisms
where
![]() $\mathbb {D}(\mathcal {G})(k):=\mathbb {D}(\mathcal {G})(k \to k)$
.
$\mathbb {D}(\mathcal {G})(k):=\mathbb {D}(\mathcal {G})(k \to k)$
.
Let
![]() $P^1 \subset \mathbb {D}(\mathcal {G})(k)$
be the Hodge filtration. We may identify
$P^1 \subset \mathbb {D}(\mathcal {G})(k)$
be the Hodge filtration. We may identify
![]() $ {\mathrm {Lift}} (P(\mathcal {Q})_{k}, (s^*\mathcal {Q})_{k[[t]]/t^2})$
with the set of lifts
$ {\mathrm {Lift}} (P(\mathcal {Q})_{k}, (s^*\mathcal {Q})_{k[[t]]/t^2})$
with the set of lifts
![]() $\mathscr {P} \subset \mathbb {D}(\mathcal {G})(k) \otimes _k k[[t]]/t^2$
of the Hodge filtration
$\mathscr {P} \subset \mathbb {D}(\mathcal {G})(k) \otimes _k k[[t]]/t^2$
of the Hodge filtration
![]() $P^1$
. The above argument shows that, under this identification, the composition (6.1) coincides with the usual period map in the Grothendieck–Messing deformation theory for p-divisible groups. In particular, (6.1) is bijective; see [Reference MessingMes72, Chapter V, Theorem 1.6].
$P^1$
. The above argument shows that, under this identification, the composition (6.1) coincides with the usual period map in the Grothendieck–Messing deformation theory for p-divisible groups. In particular, (6.1) is bijective; see [Reference MessingMes72, Chapter V, Theorem 1.6].
The proof of Theorem 6.2.1 is complete.
6.3 Classifications of p-divisible groups
For a ring R, let
![]() $\mathrm {BT}(R)$
be the category of p-divisible groups over
$\mathrm {BT}(R)$
be the category of p-divisible groups over
![]() $ \mathrm {Spec} R$
. Recall that
$ \mathrm {Spec} R$
. Recall that
![]() $ \mathrm {BK}_{\mathrm {min}}(A, I) $
is the category of minuscule Breuil–Kisin modules over a bounded prism
$ \mathrm {BK}_{\mathrm {min}}(A, I) $
is the category of minuscule Breuil–Kisin modules over a bounded prism
![]() $(A, I)$
.
$(A, I)$
.
Let
![]() $R \in \mathcal {C}_{W(k)}$
and let
$R \in \mathcal {C}_{W(k)}$
and let
![]() $ (\mathfrak {S}, (\mathcal {E})):=(W(k)[[t_1, \dotsc , t_n]], (\mathcal {E})) $
be a prism of Breuil–Kisin type equipped with an isomorphism
$ (\mathfrak {S}, (\mathcal {E})):=(W(k)[[t_1, \dotsc , t_n]], (\mathcal {E})) $
be a prism of Breuil–Kisin type equipped with an isomorphism
![]() $R \simeq \mathfrak {S}/\mathcal {E}$
over
$R \simeq \mathfrak {S}/\mathcal {E}$
over
![]() $W(k)$
. We set
$W(k)$
. We set
![]() $ \mathfrak {S}_m:=W(k)[[t_1, \dotsc , t_n]]/(t_1, \dotsc , t_n)^{m} $
and
$ \mathfrak {S}_m:=W(k)[[t_1, \dotsc , t_n]]/(t_1, \dotsc , t_n)^{m} $
and
![]() $R_m:=R/\mathfrak {m}^m_R$
. We remark that
$R_m:=R/\mathfrak {m}^m_R$
. We remark that
![]() $R_m$
is not a quasisyntomic ring if
$R_m$
is not a quasisyntomic ring if
![]() $m \geq 2$
and
$m \geq 2$
and
![]() $\dim R \geq 2$
. However, we still have the following result.
$\dim R \geq 2$
. However, we still have the following result.
Lemma 6.3.1. Let
![]() $R \in \mathcal {C}_{W(k)}$
and let
$R \in \mathcal {C}_{W(k)}$
and let
![]() $\mathscr {G}$
be a p-divisible group over
$\mathscr {G}$
be a p-divisible group over
![]() $ \mathrm {Spec} R_m$
for some
$ \mathrm {Spec} R_m$
for some
![]() $m \geq 1$
. Then
$m \geq 1$
. Then ![]() is a minuscule Breuil–Kisin module over
is a minuscule Breuil–Kisin module over
![]() $(\mathfrak {S}_m, (\mathcal {E}))$
.
$(\mathfrak {S}_m, (\mathcal {E}))$
.
Proof. There is a p-divisible group
![]() $\mathscr {G}'$
over
$\mathscr {G}'$
over
![]() $ \mathrm {Spec} R$
such that
$ \mathrm {Spec} R$
such that
![]() $\mathscr {G}' \times _{ \mathrm {Spec} R} \mathrm {Spec} R_m \simeq \mathscr {G}$
. (See [Reference IllusieIll85, Corollaire 4.8] for example.) Then
$\mathscr {G}' \times _{ \mathrm {Spec} R} \mathrm {Spec} R_m \simeq \mathscr {G}$
. (See [Reference IllusieIll85, Corollaire 4.8] for example.) Then ![]() is a minuscule Breuil–Kisin module over
is a minuscule Breuil–Kisin module over
![]() $(\mathfrak {S}, (\mathcal {E}))$
since R is quasisyntomic and the base change of
$(\mathfrak {S}, (\mathcal {E}))$
since R is quasisyntomic and the base change of ![]() along
along
![]() $\mathfrak {S} \to \mathfrak {S}_m$
is isomorphic to
$\mathfrak {S} \to \mathfrak {S}_m$
is isomorphic to ![]() as explained in Section 6.1. The assertion follows from this fact.
as explained in Section 6.1. The assertion follows from this fact.
We can deduce the following result from Theorem 6.2.1.
Theorem 6.3.2. For every integer
![]() $m \geq 1$
, the contravariant functor
$m \geq 1$
, the contravariant functor
is an anti-equivalence of categories.
Proof. If
![]() $m=1$
, then the assertion follows from the classical Dieudonné theory (see also Example 6.1.3). For a general
$m=1$
, then the assertion follows from the classical Dieudonné theory (see also Example 6.1.3). For a general
![]() $m \geq 1$
, it is enough to show that the functor
$m \geq 1$
, it is enough to show that the functor ![]() induces an equivalence of groupoids; see, for example, the proof of [Reference LauLau10, Theorem 3.2]. Since the assertion holds for
induces an equivalence of groupoids; see, for example, the proof of [Reference LauLau10, Theorem 3.2]. Since the assertion holds for
![]() $m=1$
, we are reduced to proving that for any p-divisible group
$m=1$
, we are reduced to proving that for any p-divisible group
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} k$
and
$ \mathrm {Spec} k$
and ![]() , the functor
, the functor ![]() induces an equivalence from the groupoid of deformations of
induces an equivalence from the groupoid of deformations of
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} R_m$
to that of deformations of M over
$ \mathrm {Spec} R_m$
to that of deformations of M over
![]() $(\mathfrak {S}_m, (\mathcal {E}))$
. By the fact that any deformation of
$(\mathfrak {S}_m, (\mathcal {E}))$
. By the fact that any deformation of
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} R_m$
has no nontrivial automorphisms and by Corollary 3.2.10, it is enough to check that the construction
$ \mathrm {Spec} R_m$
has no nontrivial automorphisms and by Corollary 3.2.10, it is enough to check that the construction ![]() induces a bijection between the sets of isomorphism classes of objects. Let
induces a bijection between the sets of isomorphism classes of objects. Let
![]() $\mathcal {G}^{ {\mathrm {univ}} }$
be a universal deformation of
$\mathcal {G}^{ {\mathrm {univ}} }$
be a universal deformation of
![]() $\mathcal {G}$
. Since
$\mathcal {G}$
. Since
![]() $\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} })$
has the property (BK) by Theorem 6.2.1, the assertion follows.
$\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} })$
has the property (BK) by Theorem 6.2.1, the assertion follows.
As a consequence, we obtain an alternative proof of the following result of Anschütz–Le Bras. A detailed comparison will be discussed at the end of this subsection.
Corollary 6.3.3 [Reference Anschütz and Le BrasALB23, Theorem 5.12].
The contravariant functor
is an anti-equivalence of categories.
Proof. The assertion follows from Theorem 6.3.2 since we have
Remark 6.3.4. Assume that
![]() $\mathfrak {S}=W(k)[[t]]$
and
$\mathfrak {S}=W(k)[[t]]$
and
![]() $\mathcal {E}$
is an Eisenstein polynomial. In this case, a classification result as in Corollary 6.3.3 was initiated by Breuil and Kisin. More precisely, Breuil conjectured that there exists an equivalence between the two categories in Corollary 6.3.3, and Kisin proved this conjecture when
$\mathcal {E}$
is an Eisenstein polynomial. In this case, a classification result as in Corollary 6.3.3 was initiated by Breuil and Kisin. More precisely, Breuil conjectured that there exists an equivalence between the two categories in Corollary 6.3.3, and Kisin proved this conjecture when
![]() $p \geq 3$
; see [Reference KisinKis06] and [Reference KisinKis09].
$p \geq 3$
; see [Reference KisinKis06] and [Reference KisinKis09].
For general R and
![]() $(\mathfrak {S}, (\mathcal {E}))=(W(k)[[t_1, \dotsc , t_n]], (\mathcal {E}))$
as above, an equivalence between the two categories in Theorem 6.3.2 was previously obtained by Lau, using crystalline Dieudonné theory and Dieudonné displays; see [Reference LauLau10] for
$(\mathfrak {S}, (\mathcal {E}))=(W(k)[[t_1, \dotsc , t_n]], (\mathcal {E}))$
as above, an equivalence between the two categories in Theorem 6.3.2 was previously obtained by Lau, using crystalline Dieudonné theory and Dieudonné displays; see [Reference LauLau10] for
![]() $p \geq 3$
and [Reference LauLau14, Corollary 5.4, Theorem 6.6] for any p. This result in particular implies that Breuil’s conjecture holds true for any p; see also [Reference KimKim12] and [Reference LiuLiu13].
$p \geq 3$
and [Reference LauLau14, Corollary 5.4, Theorem 6.6] for any p. This result in particular implies that Breuil’s conjecture holds true for any p; see also [Reference KimKim12] and [Reference LiuLiu13].
Let
![]() ${\mathcal O}_C$
be a p-adically complete valuation ring of rank
${\mathcal O}_C$
be a p-adically complete valuation ring of rank
![]() $1$
with algebraically closed fraction field C. The ring
$1$
with algebraically closed fraction field C. The ring
![]() ${\mathcal O}_C$
is a perfectoid ring. We write
${\mathcal O}_C$
is a perfectoid ring. We write
![]() ${\mathcal O}_{C^\flat }$
for the tilt of
${\mathcal O}_{C^\flat }$
for the tilt of
![]() ${\mathcal O}_C$
. Let
${\mathcal O}_C$
. Let
![]() $\varpi ^\flat \in {\mathcal O}_{C^\flat }$
be a pseudo-uniformizer such that
$\varpi ^\flat \in {\mathcal O}_{C^\flat }$
be a pseudo-uniformizer such that
![]() $p=0$
in
$p=0$
in
![]() ${\mathcal O}_C/\varpi $
, where
${\mathcal O}_C/\varpi $
, where
![]() $\varpi :=\theta ([\varpi ^\flat ])$
. Assume that k is the residue field of
$\varpi :=\theta ([\varpi ^\flat ])$
. Assume that k is the residue field of
![]() ${\mathcal O}_C$
. There exists a local homomorphism
${\mathcal O}_C$
. There exists a local homomorphism
![]() $s \colon W(k) \to {\mathcal O}_C$
which induces the identity
$s \colon W(k) \to {\mathcal O}_C$
which induces the identity
![]() $ {\mathrm {id}} _k \colon k \to k$
; this can be proved by the same argument as in the proof of [Reference Bhatt, Morrow and ScholzeBMS18, Theorem 13.19]. We fix such a local homomorphism s.
$ {\mathrm {id}} _k \colon k \to k$
; this can be proved by the same argument as in the proof of [Reference Bhatt, Morrow and ScholzeBMS18, Theorem 13.19]. We fix such a local homomorphism s.
Proposition 6.3.5 [Reference Fargues and FontaineFF18, Théorème 11.1.7].
Let M be a minuscule Breuil–Kisin module over
![]() $(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ], (p))$
. Let
$(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ], (p))$
. Let
![]() $M_{ {\mathrm {red}} }$
be the base change of M along the map
$M_{ {\mathrm {red}} }$
be the base change of M along the map
![]() $(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ], (p)) \to (W(k), (p))$
. Then there exist an integer
$(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ], (p)) \to (W(k), (p))$
. Then there exist an integer
![]() $n \geq 1$
and an isomorphism
$n \geq 1$
and an isomorphism
of minuscule Breuil–Kisin modules over
![]() $(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{1/p^{n}}, (p))$
which is a lift of the identity of
$(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{1/p^{n}}, (p))$
which is a lift of the identity of
![]() $M_{ {\mathrm {red}} }$
.
$M_{ {\mathrm {red}} }$
.
Proof. We set
![]() $\overline {B}:= (\varinjlim _n W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{1/p^{n}})[1/p]$
, which agrees with the ring defined in [Reference Fargues and FontaineFF18, Définition 1.10.14] (for
$\overline {B}:= (\varinjlim _n W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{1/p^{n}})[1/p]$
, which agrees with the ring defined in [Reference Fargues and FontaineFF18, Définition 1.10.14] (for
![]() ${\mathcal O}_F={\mathcal O}_{C^\flat }$
and
${\mathcal O}_F={\mathcal O}_{C^\flat }$
and
![]() $E={\mathbb Q}_p$
). By [Reference Fargues and FontaineFF18, Théorème 11.1.7], there exists a finite dimensional
$E={\mathbb Q}_p$
). By [Reference Fargues and FontaineFF18, Théorème 11.1.7], there exists a finite dimensional
![]() $W(k)[1/p]$
-vector space N together with an isomorphism
$W(k)[1/p]$
-vector space N together with an isomorphism
![]() $\phi ^*N \overset {\sim }{\to } N$
and a Frobenius equivariant isomorphism
$\phi ^*N \overset {\sim }{\to } N$
and a Frobenius equivariant isomorphism
Let
![]() $\eta _{ {\mathrm {red}} } \colon N \overset {\sim }{\to } M_{ {\mathrm {red}} }[1/p]$
be the base change of
$\eta _{ {\mathrm {red}} } \colon N \overset {\sim }{\to } M_{ {\mathrm {red}} }[1/p]$
be the base change of
![]() $\eta $
along
$\eta $
along
![]() $\overline {B} \to W(k)[1/p]$
. By composing the base change of
$\overline {B} \to W(k)[1/p]$
. By composing the base change of
![]() $\eta ^{-1}_{ {\mathrm {red}} }$
along
$\eta ^{-1}_{ {\mathrm {red}} }$
along
![]() $W(k)[1/p] \to \overline {B}$
with
$W(k)[1/p] \to \overline {B}$
with
![]() $\eta $
, we then obtain a Frobenius equivariant isomorphism
$\eta $
, we then obtain a Frobenius equivariant isomorphism
which is a lift of the identity of
![]() $M_{ {\mathrm {red}} }[1/p]$
. Since
$M_{ {\mathrm {red}} }[1/p]$
. Since
![]() $\overline {B}= (\varinjlim _n W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{1/p^{n}})[1/p]$
, there is a Frobenius equivariant isomorphism
$\overline {B}= (\varinjlim _n W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{1/p^{n}})[1/p]$
, there is a Frobenius equivariant isomorphism
for some integer
![]() $n \geq 1$
which is a lift of the identity of
$n \geq 1$
which is a lift of the identity of
![]() $M_{ {\mathrm {red}} }[1/p]$
. Now the assertion follows from Lemma 5.2.5.
$M_{ {\mathrm {red}} }[1/p]$
. Now the assertion follows from Lemma 5.2.5.
Theorem 6.3.6 [Reference LauLau18, Theorem 5.7].
The contravariant functor
is an anti-equivalence of categories.
Proof. This is a special case of [Reference LauLau18, Theorem 5.7]. Indeed, the contravariant functor
![]() $\Phi _A$
associated with
$\Phi _A$
associated with
![]() $A=W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]$
in [Reference LauLau18, (5.2)] can be identified with
$A=W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]$
in [Reference LauLau18, (5.2)] can be identified with ![]() by [Reference Anschütz and Le BrasALB23, Lemma 4.45] and [Reference Cais and LauCL17, Lemma 2.1.16]. (The proof of [Reference LauLau18, Theorem 5.7] relies on Gabber’s classification of p-divisible groups over perfect rings of characteristic p, which is also proved in [Reference LauLau13, Theorem D]. In fact, Berthelot’s classification [Reference BerthelotBer80, Corollaire 3.4.3] of p-divisible groups over perfect valuation rings of characteristic p is enough for the proof of Theorem 6.3.6.)
by [Reference Anschütz and Le BrasALB23, Lemma 4.45] and [Reference Cais and LauCL17, Lemma 2.1.16]. (The proof of [Reference LauLau18, Theorem 5.7] relies on Gabber’s classification of p-divisible groups over perfect rings of characteristic p, which is also proved in [Reference LauLau13, Theorem D]. In fact, Berthelot’s classification [Reference BerthelotBer80, Corollaire 3.4.3] of p-divisible groups over perfect valuation rings of characteristic p is enough for the proof of Theorem 6.3.6.)
By combining Theorem 6.2.1, Proposition 6.3.5 and Theorem 6.3.6, we obtain the following result:
Theorem 6.3.7. For every integer
![]() $m \geq 1$
, the contravariant functor
$m \geq 1$
, the contravariant functor
is an anti-equivalence of categories.
Proof. If
![]() $m=1$
, then this is Theorem 6.3.6. For a general
$m=1$
, then this is Theorem 6.3.6. For a general
![]() $m \geq 1$
, arguing as in the proof of Theorem 6.3.2, we are reduced to proving that for any p-divisible group
$m \geq 1$
, arguing as in the proof of Theorem 6.3.2, we are reduced to proving that for any p-divisible group
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} {\mathcal O}_C/\varpi $
and
$ \mathrm {Spec} {\mathcal O}_C/\varpi $
and
the construction ![]() induces a bijection between the set
induces a bijection between the set
![]() $ {\mathrm {Def}} (\mathcal {G})_{{\mathcal O}_C/\varpi ^m}$
of isomorphism classes of deformations of
$ {\mathrm {Def}} (\mathcal {G})_{{\mathcal O}_C/\varpi ^m}$
of isomorphism classes of deformations of
![]() $\mathcal {G}$
over
$\mathcal {G}$
over
![]() $ \mathrm {Spec} {\mathcal O}_C/\varpi ^m$
and the set of isomorphism classes of deformations of M over
$ \mathrm {Spec} {\mathcal O}_C/\varpi ^m$
and the set of isomorphism classes of deformations of M over
![]() $(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{m}, I_{{\mathcal O}_C})$
.
$(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{m}, I_{{\mathcal O}_C})$
.
By Proposition 6.3.5, Theorem 6.3.6 and the classical Dieudonné theory, we may assume that
![]() $\mathcal {G}$
is the base change of a p-divisible group
$\mathcal {G}$
is the base change of a p-divisible group
![]() $\mathcal {G}_0$
over
$\mathcal {G}_0$
over
![]() $ \mathrm {Spec} k$
along the section
$ \mathrm {Spec} k$
along the section
![]() $k \to {\mathcal O}_C/\varpi $
after replacing
$k \to {\mathcal O}_C/\varpi $
after replacing
![]() $\varpi ^\flat $
by
$\varpi ^\flat $
by
![]() $(\varpi ^\flat )^{1/p^n}$
for some n. Let
$(\varpi ^\flat )^{1/p^n}$
for some n. Let
![]() $\mathcal {G}^{ {\mathrm {univ}} }_0$
be a universal deformation of
$\mathcal {G}^{ {\mathrm {univ}} }_0$
be a universal deformation of
![]() $\mathcal {G}_0$
over
$\mathcal {G}_0$
over
![]() $ \mathrm {Spec} R$
for some
$ \mathrm {Spec} R$
for some
![]() $R \in \mathcal {C}_{W(k)}$
. Let
$R \in \mathcal {C}_{W(k)}$
. Let
![]() $e \colon R \to {\mathcal O}_C/\varpi $
be the composition
$e \colon R \to {\mathcal O}_C/\varpi $
be the composition
![]() $R \to k \to {\mathcal O}_C/\varpi $
. By [Reference LauLau14, Remark 3.12], the following map is bijective:
$R \to k \to {\mathcal O}_C/\varpi $
. By [Reference LauLau14, Remark 3.12], the following map is bijective:
Then the assertion follows since
![]() $\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }_0)$
has the property (Perfd) by Theorem 6.2.1.
$\mathfrak {Q}(\mathcal {G}^{ {\mathrm {univ}} }_0)$
has the property (Perfd) by Theorem 6.2.1.
To the best of our knowledge, Theorem 6.3.7 is a new result. As a consequence, we can give an alternative proof of (the first part of) the following result.
Corollary 6.3.8 [Reference BerthelotBer80], [Reference LauLau18], [Reference Scholze and WeinsteinSW20], [Reference Anschütz and Le BrasALB23].
-
(1) The contravariant functor
is an anti-equivalence of categories.
-
(2) Let S be a perfectoid ring. The contravariant functor
is an anti-equivalence of categories.
Proof. (1) As in the proof of Corollary 6.3.3, the assertion follows from Theorem 6.3.7.
(2) As explained in [Reference Scholze and WeinsteinSW20, Theorem 17.5.2] and [Reference ItoIto21, Section 5], the assertion follows from (1) (and the classical Dieudonné theory) by using p-complete
![]() $ {\mathrm {arc}} $
-descent for finite projective modules over perfectoid rings S and over
$ {\mathrm {arc}} $
-descent for finite projective modules over perfectoid rings S and over
![]() $W(S^\flat )$
.
$W(S^\flat )$
.
We compare our results with previous studies in more detail.
Remark 6.3.9. Let the notation be as in Corollary 6.3.8. An equivalence
was originally constructed by Scholze–Weinstein in [Reference Scholze and WeinsteinSW20, Theorem 14.4.1] (resp. [Reference Scholze and WeinsteinSW20, Theorem 17.5.2], see also [Reference ItoIto21, Section 5]). If
![]() $p \geq 3$
, then such equivalences were also obtained by Lau [Reference LauLau18, Theorem 9.8] independently. Corollary 6.3.8 itself was proved in [Reference Anschütz and Le BrasALB23, Corollary 4.49] by showing that the dual of the contravariant functor
$p \geq 3$
, then such equivalences were also obtained by Lau [Reference LauLau18, Theorem 9.8] independently. Corollary 6.3.8 itself was proved in [Reference Anschütz and Le BrasALB23, Corollary 4.49] by showing that the dual of the contravariant functor ![]() coincides with the equivalence constructed in [Reference Scholze and WeinsteinSW20].
coincides with the equivalence constructed in [Reference Scholze and WeinsteinSW20].
Remark 6.3.10. Assume that C is of characteristic
![]() $0$
. We consider the following categories:
$0$
. We consider the following categories:
-
•
 $\mathcal {C}_1:=\mathrm {BT}({\mathcal O}_C)$
.
$\mathcal {C}_1:=\mathrm {BT}({\mathcal O}_C)$
. -
•
 $\mathcal {C}_2:=\mathrm {BK}_{\mathrm {min}}(W({\mathcal O}_{C^\flat }), I_{{\mathcal O}_C})$
.
$\mathcal {C}_2:=\mathrm {BK}_{\mathrm {min}}(W({\mathcal O}_{C^\flat }), I_{{\mathcal O}_C})$
. -
• The category
 $\mathcal {C}_3$
of free
$\mathcal {C}_3$
of free
 ${\mathbb Z}_p$
-modules T of finite rank together with a C-subspace of
${\mathbb Z}_p$
-modules T of finite rank together with a C-subspace of
 $T \otimes _{{\mathbb Z}_p} C$
.
$T \otimes _{{\mathbb Z}_p} C$
.
It is a theorem of Fargues that
![]() $\mathcal {C}_2$
is equivalent to
$\mathcal {C}_2$
is equivalent to
![]() $\mathcal {C}_3$
; see [Reference Scholze and WeinsteinSW20, Theorem 14.1.1]. Scholze–Weinstein proved that
$\mathcal {C}_3$
; see [Reference Scholze and WeinsteinSW20, Theorem 14.1.1]. Scholze–Weinstein proved that
![]() $\mathcal {C}_1$
is equivalent to
$\mathcal {C}_1$
is equivalent to
![]() $\mathcal {C}_3$
in [Reference Scholze and WeinsteinSW13, Theorem B]. Then, by using Fargues’ theorem, they obtained that
$\mathcal {C}_3$
in [Reference Scholze and WeinsteinSW13, Theorem B]. Then, by using Fargues’ theorem, they obtained that
![]() $\mathcal {C}_1$
is equivalent to
$\mathcal {C}_1$
is equivalent to
![]() $\mathcal {C}_2$
; see [Reference Scholze and WeinsteinSW20, Theorem 14.4.1]. Our proof of Corollary 6.3.8 (1) does not use [Reference Scholze and WeinsteinSW13, Theorem B]. Consequently, together with Fargues’ theorem, we obtain an alternative proof of [Reference Scholze and WeinsteinSW13, Theorem B]. If C is of characteristic p, then Corollary 6.3.8 (1) follows from [Reference BerthelotBer80, Corollaire 3.4.3] (and [Reference Anschütz and Le BrasALB23, Lemma 4.45]), and our proof does not give any new information.
$\mathcal {C}_2$
; see [Reference Scholze and WeinsteinSW20, Theorem 14.4.1]. Our proof of Corollary 6.3.8 (1) does not use [Reference Scholze and WeinsteinSW13, Theorem B]. Consequently, together with Fargues’ theorem, we obtain an alternative proof of [Reference Scholze and WeinsteinSW13, Theorem B]. If C is of characteristic p, then Corollary 6.3.8 (1) follows from [Reference BerthelotBer80, Corollaire 3.4.3] (and [Reference Anschütz and Le BrasALB23, Lemma 4.45]), and our proof does not give any new information.
Remark 6.3.11. Let S be a quasisyntomic ring. Recall the category
![]() $\mathrm {DM}(S)$
of prismatic Dieudonné crystals on
$\mathrm {DM}(S)$
of prismatic Dieudonné crystals on ![]() from Remark 6.1.2. Let
from Remark 6.1.2. Let
be the full subcategory of admissible prismatic Dieudonné crystals over S in the sense of [Reference Anschütz and Le BrasALB23, Definition 4.5]. By [Reference Anschütz and Le BrasALB23, Theorem 4.74], we have the following anti-equivalence:
Its proof uses [Reference Scholze and WeinsteinSW20, Theorem 17.5.2] mentioned in Remark 6.3.9.
In [Reference Anschütz and Le BrasALB23, Section 5.2] and [Reference ItoIto23, Proposition 7.1.1], the following equivalences are obtained (without using p-divisible groups):
where the second functor is defined by
![]() $\mathcal {M} \mapsto \mathcal {M}(\mathfrak {S}, (\mathcal {E}))$
. In [Reference Anschütz and Le BrasALB23, Theorem 5.12], Anschütz–Le Bras proved Corollary 6.3.3 by combining this result and (6.2).
$\mathcal {M} \mapsto \mathcal {M}(\mathfrak {S}, (\mathcal {E}))$
. In [Reference Anschütz and Le BrasALB23, Theorem 5.12], Anschütz–Le Bras proved Corollary 6.3.3 by combining this result and (6.2).
On the other hand, by using the classification results of p-divisible groups obtained in [Reference Anschütz and Le BrasALB23] and in this paper, one can show the following:
Corollary 6.3.12. Let
![]() $m \geq 1$
be an integer. We assume that
$m \geq 1$
be an integer. We assume that
![]() $\dim R =1$
. We set
$\dim R =1$
. We set
![]() $S:=R_m$
(resp.
$S:=R_m$
(resp.
![]() $S:={\mathcal O}_C/\varpi ^m$
) and
$S:={\mathcal O}_C/\varpi ^m$
) and
![]() $(A, I):=(\mathfrak {S}_m, (\mathcal {E}))$
(resp.
$(A, I):=(\mathfrak {S}_m, (\mathcal {E}))$
(resp.
![]() $(A, I):=(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{m}, I_{{\mathcal O}_C})$
). Then the functor
$(A, I):=(W({\mathcal O}_{C^\flat })/[\varpi ^\flat ]^{m}, I_{{\mathcal O}_C})$
). Then the functor
is an equivalence.
Proof. We note that S is a quasisyntomic ring by Example 6.1.1. The assertion then follows from (6.2), Theorem 6.3.2 and Theorem 6.3.7.
It would be interesting to give a direct proof of Corollary 6.3.12, without using p-divisible groups. This will be achieved in [Reference Gardner and MadapusiGM24]. See also Conjecture 7.1.2 below.
7 Consequences on prismatic F-gauges
In this section, we assume that
![]() ${\mathcal O}_E={\mathbb Z}_p$
. Let G be a smooth affine group scheme over
${\mathcal O}_E={\mathbb Z}_p$
. Let G be a smooth affine group scheme over
![]() ${\mathbb Z}_p$
and let
${\mathbb Z}_p$
and let
![]() $ \mu \colon {\mathbb G}_m \to G_{W(k)} $
be a cocharacter where k is a perfect field of characteristic p. Let R be a quasisyntomic ring over
$ \mu \colon {\mathbb G}_m \to G_{W(k)} $
be a cocharacter where k is a perfect field of characteristic p. Let R be a quasisyntomic ring over
![]() $W(k)$
. In [Reference ItoIto23, Section 8.2], we introduced the groupoid
$W(k)$
. In [Reference ItoIto23, Section 8.2], we introduced the groupoid
of prismatic G-F-gauges of type
![]() $\mu $
over R, following the theory of prismatic F-gauges introduced by Drinfeld and Bhatt–Lurie (cf. [Reference DrinfeldDri22], [Reference Bhatt and LurieBL22a], [Reference Bhatt and LurieBL22b], [Reference BhattBha22]) and the work of Guo–Li [Reference Guo and LiGL23]. We refer to [Reference ItoIto23, Section 8.2] for details.
$\mu $
over R, following the theory of prismatic F-gauges introduced by Drinfeld and Bhatt–Lurie (cf. [Reference DrinfeldDri22], [Reference Bhatt and LurieBL22a], [Reference Bhatt and LurieBL22b], [Reference BhattBha22]) and the work of Guo–Li [Reference Guo and LiGL23]. We refer to [Reference ItoIto23, Section 8.2] for details.
Here, we discuss some consequences of our deformation theory on prismatic G-F-gauges of type
![]() $\mu $
and make some conjectures. These conjectures should follow from the results in [Reference Gardner and MadapusiGM24]; see also Remark 1.1.13.
$\mu $
and make some conjectures. These conjectures should follow from the results in [Reference Gardner and MadapusiGM24]; see also Remark 1.1.13.
7.1 Prismatic G-F-gauges of type
 $\mu $
$\mu $
Let R be a quasisyntomic ring over
![]() $W(k)$
. The relation between prismatic G-F-gauges of type
$W(k)$
. The relation between prismatic G-F-gauges of type
![]() $\mu $
over R and prismatic G-
$\mu $
over R and prismatic G-
![]() $\mu $
-displays over R can be described as follows:
$\mu $
-displays over R can be described as follows:
Proposition 7.1.1. There exists a fully faithful functor
This functor is an equivalence if R is a perfectoid ring over
![]() $W(k)$
or a complete regular local ring over
$W(k)$
or a complete regular local ring over
![]() $W(k)$
with residue field k. In particular, we have
$W(k)$
with residue field k. In particular, we have
Proof. See [Reference ItoIto23, Proposition 8.2.11, Corollary 8.2.12].
Let
![]() $R \in \mathcal {C}_{W(k)}$
be a complete regular local ring over
$R \in \mathcal {C}_{W(k)}$
be a complete regular local ring over
![]() $W(k)$
with residue field k. Let
$W(k)$
with residue field k. Let
![]() $ (\mathfrak {S}, (\mathcal {E})):=(W(k)[[t_1, \dotsc , t_n]], (\mathcal {E})) $
be a prism of Breuil–Kisin type with an isomorphism
$ (\mathfrak {S}, (\mathcal {E})):=(W(k)[[t_1, \dotsc , t_n]], (\mathcal {E})) $
be a prism of Breuil–Kisin type with an isomorphism
![]() $R \simeq \mathfrak {S}/\mathcal {E}$
over
$R \simeq \mathfrak {S}/\mathcal {E}$
over
![]() $W(k)$
. By Theorem 2.6.5 and Proposition 7.1.1, we have the following equivalences:
$W(k)$
. By Theorem 2.6.5 and Proposition 7.1.1, we have the following equivalences:
when
![]() $\mu $
is 1-bounded. Similarly to what we have seen in Section 4, these equivalences enable us to study the groupoid
$\mu $
is 1-bounded. Similarly to what we have seen in Section 4, these equivalences enable us to study the groupoid ![]() using
using ![]() . The former is conceptually important, while the latter is useful from a practical viewpoint. The following analogous statement should hold true.
. The former is conceptually important, while the latter is useful from a practical viewpoint. The following analogous statement should hold true.
Conjecture 7.1.2. We assume that
![]() $\mu $
is 1-bounded.
$\mu $
is 1-bounded.
-
(1) We assume that
 $\dim R =1$
. For every integer
$\dim R =1$
. For every integer
 $m \geq 1$
, the natural functor is an equivalence.
$m \geq 1$
, the natural functor is an equivalence.
-
(2) Let
 $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
 $W(k)$
. For every integer
$W(k)$
. For every integer
 $m \geq 1$
, the natural functor is an equivalence.
$m \geq 1$
, the natural functor is an equivalence.
We assume that
![]() $G= {\mathrm {GL}} _{N}$
. Let R be a quasisyntomic ring over
$G= {\mathrm {GL}} _{N}$
. Let R be a quasisyntomic ring over
![]() $W(k)$
. A prismatic
$W(k)$
. A prismatic
![]() $ {\mathrm {GL}} _{N}$
-F-gauge of type
$ {\mathrm {GL}} _{N}$
-F-gauge of type
![]() $\mu $
over R can be viewed as a prismatic F-gauge in vector bundles over R (with some additional condition) in the sense of Drinfeld and Bhatt–Lurie. By [Reference Guo and LiGL23, Theorem 2.54], the category
$\mu $
over R can be viewed as a prismatic F-gauge in vector bundles over R (with some additional condition) in the sense of Drinfeld and Bhatt–Lurie. By [Reference Guo and LiGL23, Theorem 2.54], the category
![]() $\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over R (see Remark 6.3.11) is equivalent to that of prismatic F-gauges in vector bundles ‘of weight
$\mathrm {DM}^{\mathrm {adm}}(R)$
of admissible prismatic Dieudonné crystals over R (see Remark 6.3.11) is equivalent to that of prismatic F-gauges in vector bundles ‘of weight
![]() $[0, 1]$
’ over R. In particular, we have the following conclusion:
$[0, 1]$
’ over R. In particular, we have the following conclusion:
Example 7.1.3. Let
![]() $\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _{N}$
be a cocharacter defined as in Example 2.4.7. We define
$\mu \colon {\mathbb G}_m \to {\mathrm {GL}} _{N}$
be a cocharacter defined as in Example 2.4.7. We define
which is a full subcategory of the category
![]() $\mathrm {DM}(R)$
of prismatic Dieudonné crystals on
$\mathrm {DM}(R)$
of prismatic Dieudonné crystals on ![]() . By Example 2.4.7, we have
. By Example 2.4.7, we have ![]() Let
Let
be the full subcategory of those objects that are admissible. Then we have
and the functor (7.1) can be identified with the inclusion
This follows from [Reference ItoIto23, Example 8.2.9] and [Reference Guo and LiGL23, Theorem 2.54].
7.2 Deformations of prismatic G-F-gauges of type
 $\mu $
$\mu $
We conclude this paper by discussing how our deformation theory should be interpreted in terms of deformations of prismatic G-F-gauges of type
![]() $\mu $
. We assume that
$\mu $
. We assume that
![]() $\mu $
is 1-bounded.
$\mu $
is 1-bounded.
Let
be a prismatic G-F-gauge of type
![]() $\mu $
over k. For a complete noetherian local ring R over
$\mu $
over k. For a complete noetherian local ring R over
![]() $W(k)$
with residue field k which is quasisyntomic, the set of isomorphism classes of deformations
$W(k)$
with residue field k which is quasisyntomic, the set of isomorphism classes of deformations ![]() of
of
![]() $\mathscr {Q}$
over R (defined in the usual way) is denoted by
$\mathscr {Q}$
over R (defined in the usual way) is denoted by
![]() $ {\mathrm {Def}} (\mathscr {Q})_R. $
Recall that
$ {\mathrm {Def}} (\mathscr {Q})_R. $
Recall that
![]() $\mathcal {C}_{W(k)}$
is the category of complete regular local rings over
$\mathcal {C}_{W(k)}$
is the category of complete regular local rings over
![]() $W(k)$
with residue field k. The following result can be deduced from our deformation theory.
$W(k)$
with residue field k. The following result can be deduced from our deformation theory.
Theorem 7.2.1. Assume that
![]() $\mu $
is 1-bounded. Then the functor
$\mu $
is 1-bounded. Then the functor
is representable by
![]() $R_{G, \mu }$
.
$R_{G, \mu }$
.
Let ![]() be a deformation of
be a deformation of
![]() $\mathscr {Q}$
which represents the functor
$\mathscr {Q}$
which represents the functor
![]() $ {\mathrm {Def}} (\mathscr {Q}). $
We expect that
$ {\mathrm {Def}} (\mathscr {Q}). $
We expect that
![]() $\mathscr {Q}^{\mathrm {univ}}$
is universal in a larger class of deformations of
$\mathscr {Q}^{\mathrm {univ}}$
is universal in a larger class of deformations of
![]() $\mathscr {Q}$
. For example, we have the following conjecture:
$\mathscr {Q}$
. For example, we have the following conjecture:
Conjecture 7.2.2.
-
(1) Let R be a complete noetherian local ring over
 $W(k)$
with residue field k which is quasisyntomic. Let
$W(k)$
with residue field k which is quasisyntomic. Let
 $ {\mathrm {Hom}} (R_{G, \mu }, R)_{e}$
be the set of local homomorphisms
$ {\mathrm {Hom}} (R_{G, \mu }, R)_{e}$
be the set of local homomorphisms
 $R_{G, \mu } \to R$
over
$R_{G, \mu } \to R$
over
 $W(k)$
. Then the map induced by
$W(k)$
. Then the map induced by $$\begin{align*}{\mathrm{Hom}}(R_{G, \mu}, R)_{e} \to {\mathrm{Def}}(\mathscr{Q})_R \end{align*}$$
$$\begin{align*}{\mathrm{Hom}}(R_{G, \mu}, R)_{e} \to {\mathrm{Def}}(\mathscr{Q})_R \end{align*}$$
 $\mathscr {Q}^{\mathrm {univ}}$
is bijective.
$\mathscr {Q}^{\mathrm {univ}}$
is bijective.
-
(2) Let
 $(S, a^\flat )$
be a perfectoid pair over
$(S, a^\flat )$
be a perfectoid pair over
 $W(k)$
. We regard
$W(k)$
. We regard
 $\mathscr {Q}$
as a prismatic G-F-gauge of type
$\mathscr {Q}$
as a prismatic G-F-gauge of type
 $\mu $
over
$\mu $
over
 $S/a$
by base change. Then the map induced by
$S/a$
by base change. Then the map induced by $$\begin{align*}{\mathrm{Hom}}(R_{G, \mu}, S/a^m)_{e} \to {\mathrm{Def}}(\mathscr{Q})_{S/a^m} \end{align*}$$
$$\begin{align*}{\mathrm{Hom}}(R_{G, \mu}, S/a^m)_{e} \to {\mathrm{Def}}(\mathscr{Q})_{S/a^m} \end{align*}$$
 $\mathscr {Q}^{\mathrm {univ}}$
is bijective for every
$\mathscr {Q}^{\mathrm {univ}}$
is bijective for every
 $m \geq 1$
. Here,
$m \geq 1$
. Here,
 $ {\mathrm {Def}} (\mathscr {Q})_{S/a^m}$
is the set of isomorphism classes of deformations
$ {\mathrm {Def}} (\mathscr {Q})_{S/a^m}$
is the set of isomorphism classes of deformations  of
of
 $\mathscr {Q}$
.
$\mathscr {Q}$
.
Remark 7.2.3. It follows from [Reference Anschütz and Le BrasALB23, Theorem 4.74] (see (6.2)) and the deformation theory for p-divisible groups that Conjecture 7.2.2 holds true for
![]() $G= {\mathrm {GL}} _N$
.
$G= {\mathrm {GL}} _N$
.
Remark 7.2.4.
-
(1) Let
 $R \in \mathcal {C}_{W(k)}$
and we assume that
$R \in \mathcal {C}_{W(k)}$
and we assume that
 $\dim R=1$
. Since the prismatic G-
$\dim R=1$
. Since the prismatic G-
 $\mu $
-display
$\mu $
-display
 $\mathfrak {Q}^{\mathrm {univ}}$
over
$\mathfrak {Q}^{\mathrm {univ}}$
over
 $R_{G, \mu }$
corresponding to
$R_{G, \mu }$
corresponding to
 $\mathscr {Q}^{\mathrm {univ}}$
has the property
$\mathscr {Q}^{\mathrm {univ}}$
has the property
 $(\mathrm {BK})$
by Theorem 4.1.7, we see that Conjecture 7.1.2 (1) holds true for
$(\mathrm {BK})$
by Theorem 4.1.7, we see that Conjecture 7.1.2 (1) holds true for
 $R/\mathfrak {m}^{m}_R$
if and only if Conjecture 7.2.2 (1) holds true for all
$R/\mathfrak {m}^{m}_R$
if and only if Conjecture 7.2.2 (1) holds true for all  and their deformations over
and their deformations over
 $R/\mathfrak {m}^{m}_R$
.
$R/\mathfrak {m}^{m}_R$
. -
(2) Similarly, since
 $\mathfrak {Q}^{\mathrm {univ}}$
has the property
$\mathfrak {Q}^{\mathrm {univ}}$
has the property
 $(\mathrm {Perfd})$
by Theorem 4.1.7, we see that Conjecture 7.1.2 (2) implies Conjecture 7.2.2 (2).
$(\mathrm {Perfd})$
by Theorem 4.1.7, we see that Conjecture 7.1.2 (2) implies Conjecture 7.2.2 (2).
Acknowledgements
The author would like to thank Zachary Gardner, Kentaro Inoue, Tetsushi Ito, Teruhisa Koshikawa, Arthur-César Le Bras, Yuta Takaya and Alex Youcis for helpful discussions and comments. The author also thanks the referee for many helpful comments and for pointing out a mistake in an earlier version of this paper.
Competing interest
The authors have no competing interest to declare.
Financial support
The work of the author was supported by JSPS KAKENHI Grant Numbers 22K20332, 24K16887, and 24H00015.