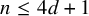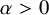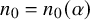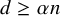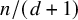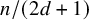1. Introduction
A Hamilton cycle in a (directed) graph is a (directed) cycle that visits every vertex. Hamilton cycles are one of the most intensely studied structures in graph theory and there are numerous results that establish (best-possible) conditions guaranteeing their existence. The seminal result of Dirac [Reference Dirac7] states that every graph on
![]() $n\ge 3$
vertices with minimum degree at least
$n\ge 3$
vertices with minimum degree at least
![]() $n/2$
is Hamiltonian. Ghouila-Houri [Reference Ghouila-Houri12] showed the corresponding version in directed graphs (digraph for short), that is, every digraph on
$n/2$
is Hamiltonian. Ghouila-Houri [Reference Ghouila-Houri12] showed the corresponding version in directed graphs (digraph for short), that is, every digraph on
![]() $n\ge 3$
vertices with minimum semi-degree at least
$n\ge 3$
vertices with minimum semi-degree at least
![]() $n/2$
(i.e., every vertex has in- and outdegree at least
$n/2$
(i.e., every vertex has in- and outdegree at least
![]() $n/2$
) is Hamiltonian. These bounds are tight by taking for instance the disjoint union of two cliques (a regular extremal example) or a slightly imbalanced complete bipartite (di)graph (an irregular extremal example). Recall that an oriented graph is a digraph that can have at most one edge between each pair of vertices (whereas a digraph can have up to two, one in each direction). For oriented graphs, a more recent result of Keevash, Kühn, and Osthus [Reference Keevash, Kühn and Osthus17] established a (tight) minimum semi-degree threshold of
$n/2$
) is Hamiltonian. These bounds are tight by taking for instance the disjoint union of two cliques (a regular extremal example) or a slightly imbalanced complete bipartite (di)graph (an irregular extremal example). Recall that an oriented graph is a digraph that can have at most one edge between each pair of vertices (whereas a digraph can have up to two, one in each direction). For oriented graphs, a more recent result of Keevash, Kühn, and Osthus [Reference Keevash, Kühn and Osthus17] established a (tight) minimum semi-degree threshold of
![]() $\lceil (3n - 4)/8 \rceil $
for Hamiltonicity. In contrast to graphs and digraphs, there are no regular extremal examples for this result. Jackson [Reference Jackson16] conjectured in 1981 that regularity actually reduces the degree threshold significantly for oriented graphs:
$\lceil (3n - 4)/8 \rceil $
for Hamiltonicity. In contrast to graphs and digraphs, there are no regular extremal examples for this result. Jackson [Reference Jackson16] conjectured in 1981 that regularity actually reduces the degree threshold significantly for oriented graphs:
Conjecture 1.1 (Jackson [Reference Jackson16])
For each
![]() $d> 2$
, every d-regular oriented graph (i.e., every vertex has d in- and outneighbours) on
$d> 2$
, every d-regular oriented graph (i.e., every vertex has d in- and outneighbours) on
![]() $n\leq 4d+1$
vertices has a Hamilton cycle.
$n\leq 4d+1$
vertices has a Hamilton cycle.
The disjoint union of two regular tournaments shows that Jackson’s conjecture is best possible. This example works for
![]() $n\equiv 2\ \pmod {4}$
(since regular tournaments require an odd number of vertices), but similar examples exist for
$n\equiv 2\ \pmod {4}$
(since regular tournaments require an odd number of vertices), but similar examples exist for
![]() $n\equiv 0,1,3\ \pmod {4}$
(see Section 1.2).
$n\equiv 0,1,3\ \pmod {4}$
(see Section 1.2).
We note that an approximate version of Jackson’s conjecture was recently verified by the current authors in [Reference Lo, Patel and Yıldız27], that is, for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $n_0(\varepsilon )$
such that every d-regular oriented graph on
$n_0(\varepsilon )$
such that every d-regular oriented graph on
![]() $n\ge n_0(\varepsilon )$
vertices with
$n\ge n_0(\varepsilon )$
vertices with
![]() $d\ge (1/4+\varepsilon )n$
is Hamiltonian. Here, we verify the exact version for large n.
$d\ge (1/4+\varepsilon )n$
is Hamiltonian. Here, we verify the exact version for large n.
Theorem 1.2. There exists an integer
![]() $n_0$
such that every d-regular oriented graph on
$n_0$
such that every d-regular oriented graph on
![]() $n\ge n_0$
vertices with
$n\ge n_0$
vertices with
![]() $n\leq 4d+1$
has a Hamilton cycle.
$n\leq 4d+1$
has a Hamilton cycle.
Generalizing questions about Hamilton cycles, one can consider the question of covering the vertices of a (di)graph with as few vertex-disjoint cycles as possible. Indeed, we prove Theorem 1.2 by showing a more general result about covering regular digraphs and oriented graphs with few vertex-disjoint cycles.
Theorem 1.3. For all
![]() $\alpha>0$
, there exists
$\alpha>0$
, there exists
![]() $n_0 = n_0(\alpha )$
such that every d-regular digraph G on
$n_0 = n_0(\alpha )$
such that every d-regular digraph G on
![]() $n\geq n_0$
vertices with
$n\geq n_0$
vertices with
![]() $d \ge \alpha n $
can be covered by at most
$d \ge \alpha n $
can be covered by at most
![]() $n/(d+1)$
vertex-disjoint cycles. Moreover, if G is an oriented graph, then at most
$n/(d+1)$
vertex-disjoint cycles. Moreover, if G is an oriented graph, then at most
![]() $n/(2d+1)$
cycles suffice.
$n/(2d+1)$
cycles suffice.
This is best possible by considering the disjoint union of complete digraphs of order
![]() $d+1$
for digraphs and the disjoint union of regular tournaments of order
$d+1$
for digraphs and the disjoint union of regular tournaments of order
![]() $2d+1$
for oriented graphs. Notice that we have
$2d+1$
for oriented graphs. Notice that we have
![]() $n/(2d+1)<2$
when
$n/(2d+1)<2$
when
![]() $n\leq 4d+1$
, so that Theorem 1.3 implies Theorem 1.2. We also point out that the proof of Theorem 1.3 in fact shows that each cycle is relatively long (of length at least
$n\leq 4d+1$
, so that Theorem 1.3 implies Theorem 1.2. We also point out that the proof of Theorem 1.3 in fact shows that each cycle is relatively long (of length at least
![]() $d/2$
).
$d/2$
).
Theorem 1.3 generalizes the following result of Gruslys and Letzter [Reference Gruslys and Letzter13] from regular graphs to regular digraphs and oriented graphs.
Theorem 1.4 (Gruslys and Letzter [Reference Gruslys and Letzter13])
For all
![]() $\alpha>0$
, there exists
$\alpha>0$
, there exists
![]() $n_0 = n_0(\alpha )$
such that every d-regular graph on
$n_0 = n_0(\alpha )$
such that every d-regular graph on
![]() $n \ge n_0$
vertices with
$n \ge n_0$
vertices with
![]() $d \ge \alpha n $
can be covered by at most
$d \ge \alpha n $
can be covered by at most
![]() $n/(d+1)$
vertex-disjoint cycles.
$n/(d+1)$
vertex-disjoint cycles.
Theorem 1.3 implies Theorem 1.4 by making every edge into a directed
![]() $2$
-cycle.
$2$
-cycle.
1.1. Related work
Theorem 1.3 also has connections with several well-studied problems in extremal graph theory: here we mention some of them.
1.1.1. Path cover
A weaker version of cycle cover is path cover. The path cover number of a (di)graph G, denoted by
![]() $\pi (G)$
, is the minimum number of vertex-disjoint (directed) paths needed to cover
$\pi (G)$
, is the minimum number of vertex-disjoint (directed) paths needed to cover
![]() $V(G)$
. This was introduced by Ore [Reference Ore30], and he showed that
$V(G)$
. This was introduced by Ore [Reference Ore30], and he showed that
![]() $\pi (G)\leq n-\sigma _2(G)$
holds where
$\pi (G)\leq n-\sigma _2(G)$
holds where
![]() $\sigma _2(G)$
denotes the minimum sum of the degrees over all non-adjacent vertices. Magnant and Martin [Reference Magnant and Martin28] conjectured that regularity significantly reduces the upper bound for
$\sigma _2(G)$
denotes the minimum sum of the degrees over all non-adjacent vertices. Magnant and Martin [Reference Magnant and Martin28] conjectured that regularity significantly reduces the upper bound for
![]() $\pi (G)$
:
$\pi (G)$
:
Conjecture 1.5 (Magnant and Martin [Reference Magnant and Martin28])
If G is a d-regular graph on n vertices, then
![]() $\pi (G)\leq n/(d+1)$
.
$\pi (G)\leq n/(d+1)$
.
It is known that Conjecture 1.5 holds for small values of d (see [Reference Magnant and Martin28] for
![]() $d\leq 5$
and see [Reference Feige and Fuchs9] for
$d\leq 5$
and see [Reference Feige and Fuchs9] for
![]() $d=6$
). Han [Reference Han15] showed that, for dense graphs, it is enough to use
$d=6$
). Han [Reference Han15] showed that, for dense graphs, it is enough to use
![]() $1+n/(d+1)$
paths to cover almost all vertices. Also, Theorem 1.4 verifies Conjecture 1.5 in the dense case. It is worth noting that the Linear Arboricity Conjecture [Reference Akiyama, Exoo and Harary2] implies Conjecture 1.5 for odd values of d, and gives
$1+n/(d+1)$
paths to cover almost all vertices. Also, Theorem 1.4 verifies Conjecture 1.5 in the dense case. It is worth noting that the Linear Arboricity Conjecture [Reference Akiyama, Exoo and Harary2] implies Conjecture 1.5 for odd values of d, and gives
![]() $\pi (G)\leq 2n/(d+2)$
for general d (see [Reference Feige and Fuchs9] for a detailed discussion).
$\pi (G)\leq 2n/(d+2)$
for general d (see [Reference Feige and Fuchs9] for a detailed discussion).
For digraphs, the classical result of Gallai and Milgram [Reference Gallai and Milgram11] states that
![]() $\pi (G)$
can be bounded above by the size of the maximum independent set (and Dilworth’s [Reference Dilworth6] theorem says that equality holds for the special case of posets). As our Theorem 1.3 generalizes Theorem 1.4 from graphs to digraphs and oriented graphs, we believe the following stronger version of Conjecture 1.5 holds, which Theorem 1.3 establishes in the dense case.
$\pi (G)$
can be bounded above by the size of the maximum independent set (and Dilworth’s [Reference Dilworth6] theorem says that equality holds for the special case of posets). As our Theorem 1.3 generalizes Theorem 1.4 from graphs to digraphs and oriented graphs, we believe the following stronger version of Conjecture 1.5 holds, which Theorem 1.3 establishes in the dense case.
Conjecture 1.6. If G is a d-regular digraph on n vertices, then
![]() $\pi (G)\leq n/(d+1)$
. Moreover,
$\pi (G)\leq n/(d+1)$
. Moreover,
![]() $\pi (G)\leq n/(2d+1)$
holds if G is oriented.
$\pi (G)\leq n/(2d+1)$
holds if G is oriented.
Also, Conjecture 1.6 implies Conjecture 1.5 by making every edge into a directed
![]() $2$
-cycle.
$2$
-cycle.
1.1.2. Extending perfect matchings
Gruslys and Letzter [Reference Gruslys and Letzter13], as well as proving Theorem 1.4, proved that every large d-regular bipartite graph G on n vertices with d linear in n can be covered by at most
![]() $n/2d$
vertex-disjoint paths. They mentioned that one should be able to replace paths by cycles. Indeed, as a corollary of Theorem 1.3, the result below shows that those cycles can be found in such a way that they even contain any prescribed perfect matching.
$n/2d$
vertex-disjoint paths. They mentioned that one should be able to replace paths by cycles. Indeed, as a corollary of Theorem 1.3, the result below shows that those cycles can be found in such a way that they even contain any prescribed perfect matching.
Corollary 1.7. For all
![]() $\alpha>0$
, there exists
$\alpha>0$
, there exists
![]() $n_1 = n_1(\alpha )$
such that, for every d-regular bipartite graph on
$n_1 = n_1(\alpha )$
such that, for every d-regular bipartite graph on
![]() $n \ge n_1$
vertices with
$n \ge n_1$
vertices with
![]() $d \ge \alpha n $
, any perfect matching can be extended to vertex-disjoint cycles covering all vertices with at most
$d \ge \alpha n $
, any perfect matching can be extended to vertex-disjoint cycles covering all vertices with at most
![]() $n/2d$
cycles.
$n/2d$
cycles.
Proof of Corollary 1.7
Let
![]() $\alpha> 0$
and
$\alpha> 0$
and
![]() $n_1 = 2 n_0(\alpha )$
, where
$n_1 = 2 n_0(\alpha )$
, where
![]() $n_0$
is the function given in Theorem 1.3. Let G be a d-regular bipartite graph on
$n_0$
is the function given in Theorem 1.3. Let G be a d-regular bipartite graph on
![]() $n \ge n_1$
vertices with
$n \ge n_1$
vertices with
![]() $d \ge \alpha n $
and vertex classes X and Y. Since G is bipartite and regular, n is even and
$d \ge \alpha n $
and vertex classes X and Y. Since G is bipartite and regular, n is even and
![]() $|X| = |Y| = n/2$
. Let M be any perfect matching of G. Let
$|X| = |Y| = n/2$
. Let M be any perfect matching of G. Let
![]() $X = \{ x_1, \dots , x_{n/2}\}$
and
$X = \{ x_1, \dots , x_{n/2}\}$
and
![]() $Y = \{y_1, \dots , y_{n/2}\}$
be such that
$Y = \{y_1, \dots , y_{n/2}\}$
be such that
![]() $x_iy_i \in E(M)$
for all i. Define the digraph H on X such that for any distinct
$x_iy_i \in E(M)$
for all i. Define the digraph H on X such that for any distinct
![]() $i,j\in [n/2]$
,
$i,j\in [n/2]$
,
![]() $x_ix_j \in E(H)$
if and only if
$x_ix_j \in E(H)$
if and only if
![]() $x_i y_j \in E(G)$
. Note that H is
$x_i y_j \in E(G)$
. Note that H is
![]() $(d-1)$
-regular on
$(d-1)$
-regular on
![]() $n/2$
vertices. By Theorem 1.3, H can be covered by at most
$n/2$
vertices. By Theorem 1.3, H can be covered by at most
![]() $n/2d$
vertex-disjoint cycles. Note that a (directed) cycle
$n/2d$
vertex-disjoint cycles. Note that a (directed) cycle
![]() $x_{i_1} x_{i_2}\dots x_{i_\ell }$
in H corresponds to a cycle
$x_{i_1} x_{i_2}\dots x_{i_\ell }$
in H corresponds to a cycle
![]() $x_{i_1} y_{i_2 } x_{i_2} y_{i_3}\dots x_{i_\ell } y_{i_1}$
in G. Therefore G can be covered by at most
$x_{i_1} y_{i_2 } x_{i_2} y_{i_3}\dots x_{i_\ell } y_{i_1}$
in G. Therefore G can be covered by at most
![]() $n/2d$
vertex-disjoint cycles that contain all the edges of M.
$n/2d$
vertex-disjoint cycles that contain all the edges of M.
Note that Corollary 1.7 is tight by considering the disjoint union of
![]() $n/2d$
many
$n/2d$
many
![]() $K_{d,d}$
’s. It also shows that d-regular bipartite graphs on n (sufficiently large) vertices with
$K_{d,d}$
’s. It also shows that d-regular bipartite graphs on n (sufficiently large) vertices with
![]() $d>n/4$
are examples of graphs in which every perfect matching can be extended into a Hamilton cycle. This property is called the PMH-property in [Reference Abreu, Gauci, Labbate, Mazzuoccolo and Zerafa1]. Häggkvist [Reference Häggkvist, Bondy and Murty14] initiated the study of sufficient conditions for the PMH-property (using the name F-Hamiltonian where F is a perfect matching) by showing
$d>n/4$
are examples of graphs in which every perfect matching can be extended into a Hamilton cycle. This property is called the PMH-property in [Reference Abreu, Gauci, Labbate, Mazzuoccolo and Zerafa1]. Häggkvist [Reference Häggkvist, Bondy and Murty14] initiated the study of sufficient conditions for the PMH-property (using the name F-Hamiltonian where F is a perfect matching) by showing
![]() $\sigma _2(G)\geq n+1$
is sufficient. Las Vergnas [Reference Vergnas24] proved a similar condition for bipartite graphs, which also (almost) implies Corollary 1.7 in the case
$\sigma _2(G)\geq n+1$
is sufficient. Las Vergnas [Reference Vergnas24] proved a similar condition for bipartite graphs, which also (almost) implies Corollary 1.7 in the case
![]() $d>n/4$
, and Yang [Reference Yang35] gave minimum edge density conditions to guarantee the PMH property in graphs and bipartite graphs. In the sparse setting, as a special case of a conjecture of Ruskey and Savage [Reference Ruskey and Savage32], Fink [Reference Fink10] proved that the hypercube has the PMH-property.
$d>n/4$
, and Yang [Reference Yang35] gave minimum edge density conditions to guarantee the PMH property in graphs and bipartite graphs. In the sparse setting, as a special case of a conjecture of Ruskey and Savage [Reference Ruskey and Savage32], Fink [Reference Fink10] proved that the hypercube has the PMH-property.
1.2. Extremal examples for Conjecture 1.1
We end the introduction with the deferred examples from earlier. Note that we give a general overview of the paper at the end of the next section.
Recall that the disjoint union of two regular tournaments on
![]() $n/2$
vertices shows that Jackson’s conjecture (Conjecture 1.1) is best possible. This example works when
$n/2$
vertices shows that Jackson’s conjecture (Conjecture 1.1) is best possible. This example works when
![]() $n \equiv 2\ \pmod {4}$
and similar examples for other values of n are constructed as follows. When
$n \equiv 2\ \pmod {4}$
and similar examples for other values of n are constructed as follows. When
![]() $n \equiv 0\ \pmod {4}$
, we take the disjoint union of two complete graphs on
$n \equiv 0\ \pmod {4}$
, we take the disjoint union of two complete graphs on
![]() $n/2$
vertices, remove a perfect matching, and orient the edges so that the resulting oriented graph is regular. When
$n/2$
vertices, remove a perfect matching, and orient the edges so that the resulting oriented graph is regular. When
![]() $n \equiv 3\ \pmod {4}$
, we take a disjoint union of a regular tournament on
$n \equiv 3\ \pmod {4}$
, we take a disjoint union of a regular tournament on
![]() $(n-1)/2$
vertices and a regular orientation of the complete graph minus a perfect matching on
$(n-1)/2$
vertices and a regular orientation of the complete graph minus a perfect matching on
![]() $(n+1)/2$
vertices. When
$(n+1)/2$
vertices. When
![]() $n \equiv 1\ \pmod {4}$
, we take a regular orientation of a disjoint union of a clique minus a perfect matching on
$n \equiv 1\ \pmod {4}$
, we take a regular orientation of a disjoint union of a clique minus a perfect matching on
![]() $(n-1)/2$
vertices and a clique minus a Hamilton cycle on
$(n-1)/2$
vertices and a clique minus a Hamilton cycle on
![]() $(n+1)/2$
vertices.
$(n+1)/2$
vertices.
2. Notation and preliminaries
Throughout the paper, we use standard graph theory notation and terminology. For
![]() $k\in \mathbb {N}$
, we sometimes denote the set
$k\in \mathbb {N}$
, we sometimes denote the set
![]() $\{1,2,\ldots ,k\}$
by
$\{1,2,\ldots ,k\}$
by
![]() $[k]$
. For a digraph G, we denote its vertex set by
$[k]$
. For a digraph G, we denote its vertex set by
![]() $V(G)$
and its edge set
$V(G)$
and its edge set
![]() $E(G)$
, and sometimes write
$E(G)$
, and sometimes write
![]() $|G| := |V(G)|$
and
$|G| := |V(G)|$
and
![]() $e(G) := |E(G)|$
. For
$e(G) := |E(G)|$
. For
![]() $a,b \in V(G)$
, we write
$a,b \in V(G)$
, we write
![]() $ab$
for the directed edge from a to b. We write
$ab$
for the directed edge from a to b. We write
![]() $H \subseteq G$
to mean H is a subdigraph of G (i.e.,
$H \subseteq G$
to mean H is a subdigraph of G (i.e.,
![]() $V(H) \subseteq V(G)$
and
$V(H) \subseteq V(G)$
and
![]() $E(H) \subseteq E(G)$
). We sometimes think of
$E(H) \subseteq E(G)$
). We sometimes think of
![]() $F \subseteq E(G)$
as a subdigraph of G with vertex set consisting of those vertices incident to edges in F and with edge set F. We write
$F \subseteq E(G)$
as a subdigraph of G with vertex set consisting of those vertices incident to edges in F and with edge set F. We write
![]() $G-F$
for the digraph obtained from G by deleting the edges in F. For
$G-F$
for the digraph obtained from G by deleting the edges in F. For
![]() $S \subseteq V(G)$
, we write
$S \subseteq V(G)$
, we write
![]() $G[S]$
for the subdigraph of G induced by S and
$G[S]$
for the subdigraph of G induced by S and
![]() $G-S$
for the digraph
$G-S$
for the digraph
![]() $G[V(G) \setminus S]$
. For
$G[V(G) \setminus S]$
. For
![]() $A,B \subseteq V(G)$
not necessarily disjoint, we define
$A,B \subseteq V(G)$
not necessarily disjoint, we define
![]() $E_G(A,B):= \{ab \in E(G): a \in A, \; b \in B \}$
and we write
$E_G(A,B):= \{ab \in E(G): a \in A, \; b \in B \}$
and we write
![]() $e_G(A,B) := |E_G(A,B)|$
Footnote 1. We often drop subscripts if these are clear from context. For two digraphs
$e_G(A,B) := |E_G(A,B)|$
Footnote 1. We often drop subscripts if these are clear from context. For two digraphs
![]() $H_1$
and
$H_1$
and
![]() $H_2$
, the union
$H_2$
, the union
![]() $H_1 \cup H_2$
is the digraph with vertex set
$H_1 \cup H_2$
is the digraph with vertex set
![]() $V(H_1) \cup V(H_2)$
and edge set
$V(H_1) \cup V(H_2)$
and edge set
![]() $E(H_1) \cup E(H_2)$
. We say an undirected graph G is bipartite with bipartition
$E(H_1) \cup E(H_2)$
. We say an undirected graph G is bipartite with bipartition
![]() $A,B$
if
$A,B$
if
![]() $V(G)=A\cup B$
and
$V(G)=A\cup B$
and
![]() $E(G) \subseteq \{ab: a \in A, \; b \in B \}$
.
$E(G) \subseteq \{ab: a \in A, \; b \in B \}$
.
For a digraph G and
![]() $v\in V(G)$
, we denote the set of outneighbours and inneighbours of v by
$v\in V(G)$
, we denote the set of outneighbours and inneighbours of v by
![]() $N_G^{+}(v)$
and
$N_G^{+}(v)$
and
![]() $N_G^{-}(v)$
, respectively, and we write
$N_G^{-}(v)$
, respectively, and we write
![]() $d_G^{+}(v):=|N_G^{+}(v)|$
and
$d_G^{+}(v):=|N_G^{+}(v)|$
and
![]() $d_G^{-}(v):=|N_G^{-}(v)|$
for the out- and indegree of v, respectively. For
$d_G^{-}(v):=|N_G^{-}(v)|$
for the out- and indegree of v, respectively. For
![]() $S\subseteq V(G)$
we write
$S\subseteq V(G)$
we write
![]() $d^{-}(v,S):= |N_G^-(v) \cap S|$
and
$d^{-}(v,S):= |N_G^-(v) \cap S|$
and
![]() $d^{+}(v,S):= |N_G^+(v) \cap S|$
. We write
$d^{+}(v,S):= |N_G^+(v) \cap S|$
. We write
![]() $\delta ^+(G)$
and
$\delta ^+(G)$
and
![]() $\delta ^-(G)$
, respectively, for the minimum out- and indegree of G and
$\delta ^-(G)$
, respectively, for the minimum out- and indegree of G and
![]() $\delta ^{0}(G):=\min \{\delta ^{+}(G),\delta ^{-}(G)\}$
for the minimum semi-degree. Similarly, the maximum semi-degree
$\delta ^{0}(G):=\min \{\delta ^{+}(G),\delta ^{-}(G)\}$
for the minimum semi-degree. Similarly, the maximum semi-degree
![]() $\Delta ^{0}(G)$
of G is defined by
$\Delta ^{0}(G)$
of G is defined by
![]() $\Delta ^{0}(G):=\max \{\Delta ^{+}(G),\Delta ^{-}(G)\}$
where
$\Delta ^{0}(G):=\max \{\Delta ^{+}(G),\Delta ^{-}(G)\}$
where
![]() $\Delta ^{+}(G)$
and
$\Delta ^{+}(G)$
and
![]() $\Delta ^{-}(G)$
denote the maximum out- and maximum indegree of G, respectively. A digraph is called d-regular if each vertex has exactly d outneighbours and d inneighbours.
$\Delta ^{-}(G)$
denote the maximum out- and maximum indegree of G, respectively. A digraph is called d-regular if each vertex has exactly d outneighbours and d inneighbours.
The notation above extends to undirected graphs in the obvious ways. In particular for an undirected graph G, we write
![]() $\Delta (G)$
and
$\Delta (G)$
and
![]() $\delta (G)$
, respectively for the maximum degree and the minimum degree. A graph is called d-regular if each vertex has exactly d neighbours. For a vertex
$\delta (G)$
, respectively for the maximum degree and the minimum degree. A graph is called d-regular if each vertex has exactly d neighbours. For a vertex
![]() $v \in V(G)$
and subset
$v \in V(G)$
and subset
![]() $S \subseteq V(G)$
, we write
$S \subseteq V(G)$
, we write
![]() $d_G(v,S):=|N_G(v) \cap S|$
.
$d_G(v,S):=|N_G(v) \cap S|$
.
A directed path Q in a digraph G is a subdigraph of G such that
![]() $V(Q) = \{v_1, \ldots , v_k \}$
for some
$V(Q) = \{v_1, \ldots , v_k \}$
for some
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $E(Q) = \{v_1v_2, v_2v_3, \ldots , v_{k-1}v_k \}$
. We denote such a directed path by its vertices in order (i.e., we write
$E(Q) = \{v_1v_2, v_2v_3, \ldots , v_{k-1}v_k \}$
. We denote such a directed path by its vertices in order (i.e., we write
![]() $Q = v_1v_2 \cdots v_k$
). A directed cycle in G is exactly the same except that it also includes the edge
$Q = v_1v_2 \cdots v_k$
). A directed cycle in G is exactly the same except that it also includes the edge
![]() $v_kv_1$
. Sometimes we identify paths with their edge sets.
$v_kv_1$
. Sometimes we identify paths with their edge sets.
A set of vertex-disjoint directed paths
![]() $\mathcal {Q}=\{Q_1,Q_2,\ldots \}$
in a digraph G is called a path system in G. We interchangeably think of
$\mathcal {Q}=\{Q_1,Q_2,\ldots \}$
in a digraph G is called a path system in G. We interchangeably think of
![]() $\mathcal {Q}$
as a set of vertex-disjoint directed paths in G and as a subdigraph of G with vertex set
$\mathcal {Q}$
as a set of vertex-disjoint directed paths in G and as a subdigraph of G with vertex set
![]() $V(\mathcal {Q}) = \bigcup _{i} V(Q_i)$
and edge set
$V(\mathcal {Q}) = \bigcup _{i} V(Q_i)$
and edge set
![]() $E(\mathcal {Q}) = \bigcup _{i} E(Q_i)$
. We sometimes call this subdigraph the graph induced by
$E(\mathcal {Q}) = \bigcup _{i} E(Q_i)$
. We sometimes call this subdigraph the graph induced by
![]() $\mathcal {Q}$
. A matching M in a digraph (or undirected graph) G is a set of edges
$\mathcal {Q}$
. A matching M in a digraph (or undirected graph) G is a set of edges
![]() $M \subseteq E(G)$
such that every vertex of G is incident to at most one edge in M. If
$M \subseteq E(G)$
such that every vertex of G is incident to at most one edge in M. If
![]() $M = \{a_ib_i: i \in [m]\}$
is a matching in a digraph, then we write
$M = \{a_ib_i: i \in [m]\}$
is a matching in a digraph, then we write
![]() $V^+(M):= \{a_i : i \in [m]\}$
and
$V^+(M):= \{a_i : i \in [m]\}$
and
![]() $V^-(M) = \{ b_i : i \in [m] \}$
. A
$V^-(M) = \{ b_i : i \in [m] \}$
. A
![]() $1$
-factor in a digraph G is a set of vertex-disjoint directed cycles whose union has the same vertices as G.
$1$
-factor in a digraph G is a set of vertex-disjoint directed cycles whose union has the same vertices as G.
Throughout the paper, we will work with partitions of a vertex set V of the form
![]() $\{V_{ij}: i,j \in [k]\}$
for some
$\{V_{ij}: i,j \in [k]\}$
for some
![]() $k \in \mathbb {N}$
(so a partition into
$k \in \mathbb {N}$
(so a partition into
![]() $k^2$
parts). For each i, we write
$k^2$
parts). For each i, we write
![]() $V_{i*} := V_{i1} \cup \cdots \cup V_{ik}$
and
$V_{i*} := V_{i1} \cup \cdots \cup V_{ik}$
and
![]() $V_{*i} := V_{1i} \cup \cdots \cup V_{ki}$
. Note that
$V_{*i} := V_{1i} \cup \cdots \cup V_{ki}$
. Note that
![]() $\{V_{i*}: i \in [k]\}$
is a partition of V as is
$\{V_{i*}: i \in [k]\}$
is a partition of V as is
![]() $\{V_{*i}: i \in [k]\}$
. Note also that
$\{V_{*i}: i \in [k]\}$
. Note also that
![]() $V_{ij} = V_{i*} \cap V_{*j}$
.
$V_{ij} = V_{i*} \cap V_{*j}$
.
For two sets A and B, the symmetric difference of A and B is the set
![]() $A\triangle B := (A\setminus B) \cup (B\setminus A)$
. For
$A\triangle B := (A\setminus B) \cup (B\setminus A)$
. For
![]() $x, y \in (0,1]$
, we often use the notation
$x, y \in (0,1]$
, we often use the notation
![]() $x \ll y$
to mean that x is sufficiently small as a function of y [i.e.,
$x \ll y$
to mean that x is sufficiently small as a function of y [i.e.,
![]() $x \leq f(y)$
] for some implicitly given non-decreasing function
$x \leq f(y)$
] for some implicitly given non-decreasing function
![]() $f:(0,1] \rightarrow (0,1]$
. We implicitly assume all constants in such hierarchies are positive, and we omit floors and ceilings whenever this does not affect the argument.
$f:(0,1] \rightarrow (0,1]$
. We implicitly assume all constants in such hierarchies are positive, and we omit floors and ceilings whenever this does not affect the argument.
We use the following non-standard notation. Let G be a directed graph and let
![]() $U,W \subseteq V(G)$
not necessarily disjoint. We define
$U,W \subseteq V(G)$
not necessarily disjoint. We define
![]() $G[U,W]$
to be the auxiliary undirected bipartite graph with bipartition
$G[U,W]$
to be the auxiliary undirected bipartite graph with bipartition
![]() $U , W$
where, for each
$U , W$
where, for each
![]() $u \in U$
and
$u \in U$
and
![]() $w \in W$
,
$w \in W$
,
![]() $uv$
is an (undirected) edge of
$uv$
is an (undirected) edge of
![]() $G[U,W]$
if and only if
$G[U,W]$
if and only if
![]() $uv$
is a directed edge in
$uv$
is a directed edge in
![]() $E(G)$
. Note that for each vertex in
$E(G)$
. Note that for each vertex in
![]() $U\cap W$
, there are two copies of the vertex in
$U\cap W$
, there are two copies of the vertex in
![]() $G[U,W]$
which are viewed as distinct. So
$G[U,W]$
which are viewed as distinct. So
![]() $G[U,W]$
has
$G[U,W]$
has
![]() $|U| + |W|$
vertices and
$|U| + |W|$
vertices and
![]() $e_G(U,W)$
edges.
$e_G(U,W)$
edges.
2.1. Sketch of proof of Theorem 1.3
Theorem 1.3 is proved in several steps. One of the key ingredients is a structural result for directed graphs (Theorem 3.5) that we derive from a result of Kühn, Lo, Osthus and Staden [Reference Kühn, Lo, Osthus and Staden21] about partitioning dense regular undirected graphs into robust expanders. Robust expansion is a notion introduced and used by Kühn and Osthus together with several coauthors to obtain a number of breakthrough results on (di)graph decompositions and Hamiltonicity (see e.g., [Reference Kühn, Osthus and Treglown23, Reference Kühn and Osthus22, Reference Kühn, Lo, Osthus and Staden21]). In Section 3, we give the necessary background on robust expansion before proving Theorem 3.5, which we informally describe below.
Informally, robust expanders are dense (di)graphs that are highly connected in a certain sense, and one of their key properties is that they are Hamiltonian under suitable (mild) degree conditions (see Theorem 4.2). Moreover, they are robust to small alterations (see Lemma 3.1). If we could show that every d-regular digraph (resp. oriented graph) can be partitioned into at most
![]() $n/(d+1)$
(resp.
$n/(d+1)$
(resp.
![]() $n/(2d+1)$
) robust expanders, it would be enough to prove Theorem 1.3. Such a partition does not exist in general, but our structural result, Theorem 3.5, gives us a starting point. Roughly, it says that for any d-regular n-vertex digraph G with d linear in n and n sufficiently large, there exist two vertex partitions
$n/(2d+1)$
) robust expanders, it would be enough to prove Theorem 1.3. Such a partition does not exist in general, but our structural result, Theorem 3.5, gives us a starting point. Roughly, it says that for any d-regular n-vertex digraph G with d linear in n and n sufficiently large, there exist two vertex partitions
![]() $V(G)=V_{1*} \cup \cdots \cup V_{k*}$
and
$V(G)=V_{1*} \cup \cdots \cup V_{k*}$
and
![]() $V(G)=V_{*1} \cup \cdots \cup V_{*k}$
with
$V(G)=V_{*1} \cup \cdots \cup V_{*k}$
with
![]() $k\leq 1+n/(d+1)$
such that for each
$k\leq 1+n/(d+1)$
such that for each
![]() $i\in [k]$
,
$i\in [k]$
,
![]() $G[V_{i*}, V_{*i}]$
is a bipartite robust expander and
$G[V_{i*}, V_{*i}]$
is a bipartite robust expander and
![]() $|V_{i*}|\approx |V_{*i}|$
. Note here that k, the number of parts in each partition, is at most one more than the number of cycles we desire (in the case of digraphs). Writing
$|V_{i*}|\approx |V_{*i}|$
. Note here that k, the number of parts in each partition, is at most one more than the number of cycles we desire (in the case of digraphs). Writing
![]() $V_{ij} = V_{i*} \cap V_{*j}$
for all
$V_{ij} = V_{i*} \cap V_{*j}$
for all
![]() $i,j\in [k]$
, we can think of our two partitions as a single
$i,j\in [k]$
, we can think of our two partitions as a single
![]() $k^2$
-partition
$k^2$
-partition
![]() $\mathcal {P}=\{V_{ij}: i,j \in [k]\}$
of
$\mathcal {P}=\{V_{ij}: i,j \in [k]\}$
of
![]() $V(G)$
.
$V(G)$
.
If the partition
![]() $\mathcal {P}$
described above is balanced, meaning that
$\mathcal {P}$
described above is balanced, meaning that
![]() $|V_{i*}| = |V_{*i}|$
for all i, then it turns out that G can be covered by k vertex-disjoint cycles.Footnote 2 So to prove Theorem 1.3, we would like to ensure our partition is balanced, and when
$|V_{i*}| = |V_{*i}|$
for all i, then it turns out that G can be covered by k vertex-disjoint cycles.Footnote 2 So to prove Theorem 1.3, we would like to ensure our partition is balanced, and when
![]() $k = 1+ \lfloor n/(d+1) \rfloor $
, we would like to slightly improve on the number of cycles. For the latter, in Section 4, we define an auxiliary graph
$k = 1+ \lfloor n/(d+1) \rfloor $
, we would like to slightly improve on the number of cycles. For the latter, in Section 4, we define an auxiliary graph
![]() $S(\mathcal {P})$
for the partition
$S(\mathcal {P})$
for the partition
![]() $\mathcal {P}$
, which has vertex set
$\mathcal {P}$
, which has vertex set
![]() $[k]$
and
$[k]$
and
![]() $ij\in E(S(\mathcal {P}))$
if and only if
$ij\in E(S(\mathcal {P}))$
if and only if
![]() $V_{ij}\cup V_{ji}\neq \emptyset $
. For each connected component
$V_{ij}\cup V_{ji}\neq \emptyset $
. For each connected component
![]() $I \subseteq [k]$
of
$I \subseteq [k]$
of
![]() $S(\mathcal {P})$
, Lemma 4.1 shows how to find a cycle whose vertices are exactly
$S(\mathcal {P})$
, Lemma 4.1 shows how to find a cycle whose vertices are exactly
![]() $\bigcup _{i \in I} V_{i*} \cup V_{*i}$
(provided
$\bigcup _{i \in I} V_{i*} \cup V_{*i}$
(provided
![]() $\mathcal {P}$
is balanced). These cycles are necessarily disjoint for different connected components of
$\mathcal {P}$
is balanced). These cycles are necessarily disjoint for different connected components of
![]() $S(\mathcal {P})$
, so we obtain a cycle partition where the number of cycles is exactly the number of connected components of
$S(\mathcal {P})$
, so we obtain a cycle partition where the number of cycles is exactly the number of connected components of
![]() $S(\mathcal {P})$
. For digraphs, if
$S(\mathcal {P})$
. For digraphs, if
![]() $S(\mathcal {P})$
has at least one edge (so has at most
$S(\mathcal {P})$
has at least one edge (so has at most
![]() $k-1 \leq n/(d+1)$
connected components), then Theorem 1.3 follows. Similarly, for oriented graphs, one can show (using Proposition 6.5) that at least one edge in
$k-1 \leq n/(d+1)$
connected components), then Theorem 1.3 follows. Similarly, for oriented graphs, one can show (using Proposition 6.5) that at least one edge in
![]() $S(\mathcal {P})$
is enough to prove Theorem 1.3 for oriented graphs. Thus, it is enough if our partition
$S(\mathcal {P})$
is enough to prove Theorem 1.3 for oriented graphs. Thus, it is enough if our partition
![]() $\mathcal {P}$
is balanced and
$\mathcal {P}$
is balanced and
![]() $S(\mathcal {P})$
has at least one edge.
$S(\mathcal {P})$
has at least one edge.
To ensure our partition is balanced (i.e., that
![]() $|V_{i*}| = |V_{*i}|$
for all i), note first that, as mentioned earlier, Theorem 3.5 already guarantees that
$|V_{i*}| = |V_{*i}|$
for all i), note first that, as mentioned earlier, Theorem 3.5 already guarantees that
![]() $|V_{i*}|\approx |V_{*i}|$
for all i. The idea will be to find and contract a suitable collection of vertex-disjoint paths
$|V_{i*}|\approx |V_{*i}|$
for all i. The idea will be to find and contract a suitable collection of vertex-disjoint paths
![]() $\mathcal {Q}$
. Here suitable simply means that the numbers of edges of
$\mathcal {Q}$
. Here suitable simply means that the numbers of edges of
![]() $\mathcal {Q}$
between the various parts of
$\mathcal {Q}$
between the various parts of
![]() $\mathcal {P}$
are related in the right way, in which case we call
$\mathcal {P}$
are related in the right way, in which case we call
![]() $\mathcal {Q}$
a
$\mathcal {Q}$
a
![]() $\mathcal {P}$
-balanced path system (introduced in Section 5). If we can find such a
$\mathcal {P}$
-balanced path system (introduced in Section 5). If we can find such a
![]() $\mathcal {P}$
-balanced path system with few edges, then contracting the paths will result in a graph with an adjusted partition
$\mathcal {P}$
-balanced path system with few edges, then contracting the paths will result in a graph with an adjusted partition
![]() $\mathcal {P}'$
that is balanced and has similar properties as
$\mathcal {P}'$
that is balanced and has similar properties as
![]() $\mathcal {P}$
(Proposition 5.3), and any cycle partition in the contracted graph can be lifted to a cycle partition in the original graph (Propositions 5.1). If the path system
$\mathcal {P}$
(Proposition 5.3), and any cycle partition in the contracted graph can be lifted to a cycle partition in the original graph (Propositions 5.1). If the path system
![]() $\mathcal {Q}$
satisfies some further properties then we can also guarantee that
$\mathcal {Q}$
satisfies some further properties then we can also guarantee that
![]() $S(\mathcal {P}')$
has at least one edge and this will be enough to prove Theorem 1.3. Lemma 5.4 says that we can always find a
$S(\mathcal {P}')$
has at least one edge and this will be enough to prove Theorem 1.3. Lemma 5.4 says that we can always find a
![]() $\mathcal {P}$
-balanced path system with the required properties, and so we reduce the task of proving Theorem 1.3 to the task of proving Lemma 5.4.
$\mathcal {P}$
-balanced path system with the required properties, and so we reduce the task of proving Theorem 1.3 to the task of proving Lemma 5.4.
In Section 6 we reduce the proof of Lemma 5.4 to two lemmas, namely Lemmas 6.1 and 6.3. Lemma 6.1 allows us to find a
![]() $\mathcal {P}$
-balanced path system with the desired properties under most circumstances, while Lemma 6.3 (together with Proposition 6.2) allows us to find such a path system in the remaining ‘extremal’ circumstances when G is close to the disjoint union of cliques. Lemma 6.1 is proved in Section 7 using a flow argument and Lemma 6.3 is proved in Section 8. These last two lemmas are the most technical parts of the paper, so we defer their sketch of proofs to their respective sections.
$\mathcal {P}$
-balanced path system with the desired properties under most circumstances, while Lemma 6.3 (together with Proposition 6.2) allows us to find such a path system in the remaining ‘extremal’ circumstances when G is close to the disjoint union of cliques. Lemma 6.1 is proved in Section 7 using a flow argument and Lemma 6.3 is proved in Section 8. These last two lemmas are the most technical parts of the paper, so we defer their sketch of proofs to their respective sections.
3. Robust expanders
We first define robust expansion for graphs. Let
![]() $0 < \nu \le \tau < 1$
and let G be a graph on n vertices. For
$0 < \nu \le \tau < 1$
and let G be a graph on n vertices. For
![]() $S \subseteq V(G)$
, the
$S \subseteq V(G)$
, the
![]() $\nu $
-robust neighbourhood
$\nu $
-robust neighbourhood
![]() $RN_{\nu ,G}(S)$
is the set of all those vertices with at least
$RN_{\nu ,G}(S)$
is the set of all those vertices with at least
![]() $\nu n$
neighbours in S. We say that G is a robust
$\nu n$
neighbours in S. We say that G is a robust
![]() $(\nu , \tau )$
-expander if every
$(\nu , \tau )$
-expander if every
![]() $S \subseteq V(G)$
with
$S \subseteq V(G)$
with
![]() $\tau n \le |S| \le (1 - \tau ) n$
satisfies
$\tau n \le |S| \le (1 - \tau ) n$
satisfies
![]() $|RN_{\nu ,G} (S)| \ge |S| + \nu n$
. In fact we will mainly be concerned with bipartite robust expanders. Let G be a bipartite graph with bipartition
$|RN_{\nu ,G} (S)| \ge |S| + \nu n$
. In fact we will mainly be concerned with bipartite robust expanders. Let G be a bipartite graph with bipartition
![]() $A, B$
. We say that G is a bipartite robust
$A, B$
. We say that G is a bipartite robust
![]() $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
![]() $A, B$
if every
$A, B$
if every
![]() $S \subseteq A$
with
$S \subseteq A$
with
![]() $\tau |A| \le |S| \le (1 - \tau ) |A|$
satisfies
$\tau |A| \le |S| \le (1 - \tau ) |A|$
satisfies
![]() $|RN_{\nu ,G} (S) \cap B| \ge |S| + \nu n$
. Note that the order of A and B matters here. Our first lemma says that bipartite robust expansion is robust to small alterations; the lemma can easily be derived from the definition of robust expansion.
$|RN_{\nu ,G} (S) \cap B| \ge |S| + \nu n$
. Note that the order of A and B matters here. Our first lemma says that bipartite robust expansion is robust to small alterations; the lemma can easily be derived from the definition of robust expansion.
Lemma 3.1 [Reference Staden33, Lemma 3.4.9]
Let
![]() $0 < 1/n \ll \nu \le \tau \ll 1$
with
$0 < 1/n \ll \nu \le \tau \ll 1$
with
![]() $\nu \le 1/2$
. Let G be a bipartite graph with
$\nu \le 1/2$
. Let G be a bipartite graph with
![]() $U \subseteq V(G)$
. Suppose
$U \subseteq V(G)$
. Suppose
![]() $G[U]$
is a bipartite robust
$G[U]$
is a bipartite robust
![]() $(\nu , \tau )$
-expander on n vertices with bipartition
$(\nu , \tau )$
-expander on n vertices with bipartition
![]() $A,B$
and that
$A,B$
and that
![]() $A',B' \subseteq V(G)$
are sets satisfying
$A',B' \subseteq V(G)$
are sets satisfying
![]() $|A\triangle A'|+|B \triangle B'|\leq \nu |A|/4$
. Then
$|A\triangle A'|+|B \triangle B'|\leq \nu |A|/4$
. Then
![]() $G[ A' \cup B' ]$
is a bipartite robust
$G[ A' \cup B' ]$
is a bipartite robust
![]() $(\nu /2, 2\tau )$
-expander with bipartition
$(\nu /2, 2\tau )$
-expander with bipartition
![]() $A',B'$
.
$A',B'$
.
Next we give a structural result due to Kühn, Lo, Osthus and Staden [Reference Kühn, Lo, Osthus and Staden21] which states that any regular graph of linear minimum degree has a vertex partition into a small number of parts where each part induces a robust expander or a bipartite robust expander. In fact we state the special case of this result for bipartite graphs, which is all we require.
Theorem 3.2 (Bipartite special case of [Reference Kühn, Lo, Osthus and Staden21, Theorem 3.1])
For all
![]() $\alpha , \tau> 0$
and every non-decreasing function
$\alpha , \tau> 0$
and every non-decreasing function
![]() $f: (0, 1) \rightarrow (0, 1)$
, there exists
$f: (0, 1) \rightarrow (0, 1)$
, there exists
![]() $n_0$
such that the following holds. For all d-regular bipartite graphs G on
$n_0$
such that the following holds. For all d-regular bipartite graphs G on
![]() $2n \geq n_0$
vertices with bipartition
$2n \geq n_0$
vertices with bipartition
![]() $A,B$
and
$A,B$
and
![]() $d \ge \alpha n$
, there exist
$d \ge \alpha n$
, there exist
![]() $\rho , \nu $
with
$\rho , \nu $
with
such that there is a partition of
![]() $V(G)$
into sets
$V(G)$
into sets
![]() $A_1,\dots , A_k,B_1, \dots , B_k$
with the following properties for all
$A_1,\dots , A_k,B_1, \dots , B_k$
with the following properties for all
![]() $i \in [k]$
:
$i \in [k]$
:
-
(i)
 $G[A_i \cup B_i]$
is a bipartite robust
$G[A_i \cup B_i]$
is a bipartite robust
 $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
 $A_i,B_i$
;
$A_i,B_i$
; -
(ii) for all
 $x \in A_i \cup B_i$
and
$x \in A_i \cup B_i$
and
 $j \in [k]$
,
$j \in [k]$
,
 $d(x, A_i \cup B_i) \ge d(x, A_j \cup B_j) $
, so in particular,
$d(x, A_i \cup B_i) \ge d(x, A_j \cup B_j) $
, so in particular,
 $\delta ( G[ A_i \cup B_i ] ) \ge d/k$
;
$\delta ( G[ A_i \cup B_i ] ) \ge d/k$
; -
(iii)
 $\left | |A_i| - |B_i| \right | \le 2 \rho n$
;
$\left | |A_i| - |B_i| \right | \le 2 \rho n$
; -
(iv) all but at most
 $2 \rho n $
vertices
$2 \rho n $
vertices
 $x \in A_i \cup B_i$
satisfy
$x \in A_i \cup B_i$
satisfy
 $d(x, A_i \cup B_i) \ge d - 2 \rho n $
;
$d(x, A_i \cup B_i) \ge d - 2 \rho n $
; -
(v)
 $k \le n / (d-2 \rho n) $
;
$k \le n / (d-2 \rho n) $
; -
(vi)
 $A_1, \ldots , A_k$
is a partition of A and
$A_1, \ldots , A_k$
is a partition of A and
 $B_1, \ldots , B_k$
is a partition of B.
$B_1, \ldots , B_k$
is a partition of B.
Remark 3.3. Note that (i)–(iv) follow directly from the statement of [Reference Kühn, Lo, Osthus and Staden21, Theorem 3.1]. While (v) and (vi) cannot be deduced immediately from the statement of [Reference Kühn, Lo, Osthus and Staden21, Theorem 3.1], they follow immediately from the proof.Footnote 3
We now define robust expansion for digraphs. Let
![]() $0 < \nu \le \tau < 1$
and let G be a digraph on n vertices. For
$0 < \nu \le \tau < 1$
and let G be a digraph on n vertices. For
![]() $S \subseteq V(G)$
, the
$S \subseteq V(G)$
, the
![]() $\nu $
-robust outneighbourhood
$\nu $
-robust outneighbourhood
![]() $RN^+_{\nu ,G}(S)$
is the set of all those vertices with at least
$RN^+_{\nu ,G}(S)$
is the set of all those vertices with at least
![]() $\nu n$
inneighbours in S. We say that G is a robust
$\nu n$
inneighbours in S. We say that G is a robust
![]() $(\nu , \tau )$
-outexpander if every
$(\nu , \tau )$
-outexpander if every
![]() $S \subseteq V(G)$
with
$S \subseteq V(G)$
with
![]() $\tau n \le |S| \le (1 - \tau ) n$
satisfies
$\tau n \le |S| \le (1 - \tau ) n$
satisfies
![]() $|RN^+_{\nu ,G} (S)| \ge |S| + \nu n$
.
$|RN^+_{\nu ,G} (S)| \ge |S| + \nu n$
.
Proposition 3.4. Let
![]() $0 < 1/m \ll \nu \le \tau \ll 1$
with
$0 < 1/m \ll \nu \le \tau \ll 1$
with
![]() $\nu \le 1/2$
. Suppose G is a bipartite graph with bipartition
$\nu \le 1/2$
. Suppose G is a bipartite graph with bipartition
![]() $A,B$
, where
$A,B$
, where
![]() $A=\{a_1, \ldots , a_m\}$
and
$A=\{a_1, \ldots , a_m\}$
and
![]() $ B=\{b_1, \ldots , b_m\}$
. If G is a bipartite robust
$ B=\{b_1, \ldots , b_m\}$
. If G is a bipartite robust
![]() $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
![]() $A,B$
, then the digraph H with vertex set A and edge set
$A,B$
, then the digraph H with vertex set A and edge set
![]() $E(H) = \{a_ia_j: a_ib_j \in E(G), i \not = j\}$
is a robust
$E(H) = \{a_ia_j: a_ib_j \in E(G), i \not = j\}$
is a robust
![]() $(\nu /2, 2\tau )$
-outexpander.
$(\nu /2, 2\tau )$
-outexpander.
The proposition above follows immediately from the definitions; we crudely replace
![]() $(\nu , \tau )$
with
$(\nu , \tau )$
with
![]() $(\nu /2, 2\tau )$
to account for the loss of any edges of the form
$(\nu /2, 2\tau )$
to account for the loss of any edges of the form
![]() $a_ib_i$
.
$a_ib_i$
.
We now state and prove a structure lemma for regular digraphs that is derived from Theorem 3.2. This will be one of the key ingredients in the proof of Theorem 1.3. It says that any dense regular digraph G has two vertex partitions
![]() $V(G)=V_{1*} \cup \cdots \cup V_{k*}$
and
$V(G)=V_{1*} \cup \cdots \cup V_{k*}$
and
![]() $V(G)=V_{*1} \cup \cdots \cup V_{*k}$
with k relatively small such that for each i, the (undirected) bipartite graph
$V(G)=V_{*1} \cup \cdots \cup V_{*k}$
with k relatively small such that for each i, the (undirected) bipartite graph
![]() $G[V_{i*}, V_{*i}]$
is a bipartite robust expander (with bipartition
$G[V_{i*}, V_{*i}]$
is a bipartite robust expander (with bipartition
![]() $V_{i*}, V_{*i}$
). Various other degree and size conditions relating to the partition are also given. Note that in the theorem below, we actually give a partition
$V_{i*}, V_{*i}$
). Various other degree and size conditions relating to the partition are also given. Note that in the theorem below, we actually give a partition
![]() $\{V_{ij}: i,j \in [k]\}$
and recall that for each
$\{V_{ij}: i,j \in [k]\}$
and recall that for each
![]() $i\in [k]$
, we write
$i\in [k]$
, we write
![]() $V_{i*} := V_{i1} \cup \cdots \cup V_{ik}$
and
$V_{i*} := V_{i1} \cup \cdots \cup V_{ik}$
and
![]() $V_{*i} := V_{1i} \cup \cdots \cup V_{ki}$
. Thus
$V_{*i} := V_{1i} \cup \cdots \cup V_{ki}$
. Thus
![]() $V_{ij} = V_{i*} \cap V_{*j}$
.
$V_{ij} = V_{i*} \cap V_{*j}$
.
Theorem 3.5. For all
![]() $\alpha , \tau> 0$
and every non-decreasing function
$\alpha , \tau> 0$
and every non-decreasing function
![]() $f : (0, 1) \rightarrow (0, 1)$
, there exists
$f : (0, 1) \rightarrow (0, 1)$
, there exists
![]() $n_0$
such that the following holds. For all d-regular digraphs G on
$n_0$
such that the following holds. For all d-regular digraphs G on
![]() $n \ge n_0$
vertices with
$n \ge n_0$
vertices with
![]() $d \ge \alpha n$
, there exist
$d \ge \alpha n$
, there exist
![]() $\rho , \nu $
with
$\rho , \nu $
with
such that there is a partition
![]() $\mathcal {P} = \{ V_{ij}: i,j \in [k]\}$
of
$\mathcal {P} = \{ V_{ij}: i,j \in [k]\}$
of
![]() $V(G)$
satisfying, for all
$V(G)$
satisfying, for all
![]() $i,j \in [k]$
,
$i,j \in [k]$
,
-
(i)
 $G[V_{i*},V_{*i}]$
is a bipartite robust
$G[V_{i*},V_{*i}]$
is a bipartite robust
 $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
 $V_{i*},V_{*i}$
;
$V_{i*},V_{*i}$
; -
(ii) for all
 $x \in V_{ij}$
and
$x \in V_{ij}$
and
 $i',j' \in [k]$
,
$i',j' \in [k]$
,
 $d^+(x, V_{*i}) \ge d^+(x, V_{*i'})$
and
$d^+(x, V_{*i}) \ge d^+(x, V_{*i'})$
and
 $d^-(x, V_{j*}) \ge d^-(x, V_{j'*})$
, so in particular,
$d^-(x, V_{j*}) \ge d^-(x, V_{j'*})$
, so in particular,
 $\delta ( G [ V_{i*},V_{*i} ] ) \ge d/k$
;
$\delta ( G [ V_{i*},V_{*i} ] ) \ge d/k$
; -
(iii)
 $\left | |V_{i*}| - |V_{*i}| \right | \le 2\rho n$
;
$\left | |V_{i*}| - |V_{*i}| \right | \le 2\rho n$
; -
(iv) all but at most
 $2\rho n $
vertices
$2\rho n $
vertices
 $x \in V_{ij}$
satisfy
$x \in V_{ij}$
satisfy
 $d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - 2\rho n $
;
$d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - 2\rho n $
; -
(v)
 $k \le n / (d-2\rho n)$
.
$k \le n / (d-2\rho n)$
.
Proof. We simply apply Theorem 3.2 to the obvious bipartite graph obtained from the directed graph G, with the natural correspondence in parameters, as follows.
For any d-regular digraph G on n vertices, let
![]() $H_G$
be the d-regular bipartite undirected graph on
$H_G$
be the d-regular bipartite undirected graph on
![]() $2n$
vertices defined as follows. Let
$2n$
vertices defined as follows. Let
![]() $V(H_G) = A \cup B$
, where A and B are disjoint copies of
$V(H_G) = A \cup B$
, where A and B are disjoint copies of
![]() $V(G)$
and for
$V(G)$
and for
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
let
$b \in B$
let
![]() $ab \in E(H_G)$
if and only if
$ab \in E(H_G)$
if and only if
![]() $ab \in E(G)$
. Now applying Theorem 3.2 with
$ab \in E(G)$
. Now applying Theorem 3.2 with
![]() $H_G$
playing the role of G, we obtain the following statement.
$H_G$
playing the role of G, we obtain the following statement.
For all
![]() $\alpha , \tau> 0$
and every non-decreasing function
$\alpha , \tau> 0$
and every non-decreasing function
![]() $f: (0, 1) \rightarrow (0, 1)$
, there exists
$f: (0, 1) \rightarrow (0, 1)$
, there exists
![]() $n_0$
such that the following holds. For all d-regular digraphs G on
$n_0$
such that the following holds. For all d-regular digraphs G on
![]() $n \geq n_0$
vertices and
$n \geq n_0$
vertices and
![]() $d \ge \alpha n$
, taking
$d \ge \alpha n$
, taking
![]() $H_G$
to be the corresponding bipartite d-regular graph on
$H_G$
to be the corresponding bipartite d-regular graph on
![]() $2n \geq n_0$
vertices there exist
$2n \geq n_0$
vertices there exist
![]() $\rho , \nu $
with
$\rho , \nu $
with
such that there is a partition of
![]() $V(H_G)$
into sets
$V(H_G)$
into sets
![]() $A_1,\dots , A_{k}, B_1, \dots , B_{k}$
with the following properties for all
$A_1,\dots , A_{k}, B_1, \dots , B_{k}$
with the following properties for all
![]() $i \in [k]$
:
$i \in [k]$
:
-
(i′)
 $H_G[A_i \cup B_i]$
is a bipartite robust
$H_G[A_i \cup B_i]$
is a bipartite robust
 $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
 $A_i,B_i$
;
$A_i,B_i$
; -
(ii′) for all
 $x \in A_i \cup B_i$
and
$x \in A_i \cup B_i$
and
 $j \in [k]$
,
$j \in [k]$
,
 $d_{H_G}(x, A_i \cup B_i) \ge d_{H_G}(x, A_j \cup B_j) $
, so in particular,
$d_{H_G}(x, A_i \cup B_i) \ge d_{H_G}(x, A_j \cup B_j) $
, so in particular,
 $\delta ( H_G [ A_i \cup B_i ] ) \ge d/k$
;
$\delta ( H_G [ A_i \cup B_i ] ) \ge d/k$
; -
(iii′)
 $\left | |A_i| - |B_i| \right | \le 2 \rho n$
;
$\left | |A_i| - |B_i| \right | \le 2 \rho n$
; -
(iv′) all but at most
 $2 \rho n $
vertices
$2 \rho n $
vertices
 $x \in A_i \cup B_i$
satisfy
$x \in A_i \cup B_i$
satisfy
 $d_{H_G}(x, A_i \cup B_i) \ge d - 2 \rho n $
;
$d_{H_G}(x, A_i \cup B_i) \ge d - 2 \rho n $
; -
(v′)
 $k \le n / (d-2 \rho n)$
;
$k \le n / (d-2 \rho n)$
; -
(vi′)
 $A_1, \ldots , A_k$
is a partition of A and
$A_1, \ldots , A_k$
is a partition of A and
 $B_1, \ldots , B_k$
is a partition of B.
$B_1, \ldots , B_k$
is a partition of B.
For
![]() $i,j \in [k]$
, define
$i,j \in [k]$
, define
![]() $V_{ij} = A_i \cap B_j$
(where we think of
$V_{ij} = A_i \cap B_j$
(where we think of
![]() $A_i$
and
$A_i$
and
![]() $B_j$
as sets of vertices of the digraph G). First note that, by (vi
$B_j$
as sets of vertices of the digraph G). First note that, by (vi
![]() $'$
),
$'$
),
![]() $\mathcal {P} = \{V_{ij} : i,j \in [k] \}$
is a partition of
$\mathcal {P} = \{V_{ij} : i,j \in [k] \}$
is a partition of
![]() $V(G)$
, and
$V(G)$
, and
![]() $A_i = V_{i*}$
and
$A_i = V_{i*}$
and
![]() $B_i = V_{*i}$
. Now the natural correspondence between
$B_i = V_{*i}$
. Now the natural correspondence between
![]() $H_G$
and G means that (i
$H_G$
and G means that (i
![]() $'$
)–(v
$'$
)–(v
![]() $'$
) imply (i)–(v), respectively.
$'$
) imply (i)–(v), respectively.
4. Finding long cycles
Theorem 3.5 from the previous section shows that every (dense) regular digraph has a vertex partition with some useful properties. In this section, we show how properties (i) and (ii) from Theorem 3.5 together with a simple balancing condition on the partition allow us to construct few long cycles that can cover all the vertices of several parts in the partition.
Let G be a digraph on V and let
![]() $\mathcal {P} =\{V_{ij}:i,j \in [k]\}$
be a partition of V where we allow some parts to be empty. We say that
$\mathcal {P} =\{V_{ij}:i,j \in [k]\}$
be a partition of V where we allow some parts to be empty. We say that
![]() $\mathcal {P}$
is balanced if
$\mathcal {P}$
is balanced if
![]() $|V_{i*}| = |V_{*i}|$
for all
$|V_{i*}| = |V_{*i}|$
for all
![]() $i \in [k]$
. For
$i \in [k]$
. For
![]() $i, j \in [k]$
, let
$i, j \in [k]$
, let
![]() $G_{ij}$
be the subdigraph of G on
$G_{ij}$
be the subdigraph of G on
![]() $V_{i*} \cup V_{*j}$
with edges from
$V_{i*} \cup V_{*j}$
with edges from
![]() $V_{i*}$
to
$V_{i*}$
to
![]() $V_{*j}$
, that is,
$V_{*j}$
, that is,
![]() $E(G_{ij}) = E_G(V_{i*},V_{*j}) = E(G) \cap (V_{i*} \times V_{*j})$
.
$E(G_{ij}) = E_G(V_{i*},V_{*j}) = E(G) \cap (V_{i*} \times V_{*j})$
.
Define
![]() $S(\mathcal {P})$
to be the graph (without loops) on
$S(\mathcal {P})$
to be the graph (without loops) on
![]() $[k]$
such that for all
$[k]$
such that for all
![]() $i,j\in [k]$
with
$i,j\in [k]$
with
![]() $i\neq j$
,
$i\neq j$
,
![]() $ij \in E(S(\mathcal {P}))$
if and only if
$ij \in E(S(\mathcal {P}))$
if and only if
![]() $V_{ij} \cup V_{ji} \ne \emptyset $
. The connected components of
$V_{ij} \cup V_{ji} \ne \emptyset $
. The connected components of
![]() $S(\mathcal {P})$
will determine which parts of
$S(\mathcal {P})$
will determine which parts of
![]() $\mathcal {P}$
can be covered by one long cycle. We remark that, by definition,
$\mathcal {P}$
can be covered by one long cycle. We remark that, by definition,
![]() $\bigcup _{i\in I}(V_{i*}\cup V_{*i})$
and
$\bigcup _{i\in I}(V_{i*}\cup V_{*i})$
and
![]() $\bigcup _{j\in J}(V_{j*}\cup V_{*j})$
are disjoint for two distinct connected components I and J of
$\bigcup _{j\in J}(V_{j*}\cup V_{*j})$
are disjoint for two distinct connected components I and J of
![]() $S(\mathcal {P})$
. The aim of this section is to prove the following lemma.
$S(\mathcal {P})$
. The aim of this section is to prove the following lemma.
Lemma 4.1. Let
![]() $1/m \ll \nu \leq \tau \ll \alpha <1$
. Let G be a digraph with a balanced vertex partition
$1/m \ll \nu \leq \tau \ll \alpha <1$
. Let G be a digraph with a balanced vertex partition
![]() $\mathcal {P} = \{V_{ij} : i,j \in [k]\}$
. Let I be a connected component in
$\mathcal {P} = \{V_{ij} : i,j \in [k]\}$
. Let I be a connected component in
![]() $S(\mathcal {P})$
. Suppose that, for all
$S(\mathcal {P})$
. Suppose that, for all
![]() $i \in I$
,
$i \in I$
,
![]() $G[V_{i*},V_{*i}]$
is a bipartite robust
$G[V_{i*},V_{*i}]$
is a bipartite robust
![]() $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
![]() $V_{i*},V_{*i}$
such that
$V_{i*},V_{*i}$
such that
![]() $|V_{i*}| \ge m$
and
$|V_{i*}| \ge m$
and
![]() $\delta ( G[V_{i*},V_{*i}] ) \ge \alpha |V_{i*}|$
. Then there exists a cycle C in G with
$\delta ( G[V_{i*},V_{*i}] ) \ge \alpha |V_{i*}|$
. Then there exists a cycle C in G with
![]() $V(C) = \bigcup _{i \in I} \left ( V_{i*} \cup V_{*i} \right )$
.
$V(C) = \bigcup _{i \in I} \left ( V_{i*} \cup V_{*i} \right )$
.
The lemma above will be used as follows. Suppose we have a dense d-regular digraph G with a vertex partition
![]() $\mathcal {P}$
such as that given by Theorem 3.5 but with the additional property that
$\mathcal {P}$
such as that given by Theorem 3.5 but with the additional property that
![]() $\mathcal {P}$
is balanced. Then Lemma 4.1 applied to each connected component of
$\mathcal {P}$
is balanced. Then Lemma 4.1 applied to each connected component of
![]() $S(\mathcal {P})$
gives us a collection of s vertex-disjoint cycles that cover
$S(\mathcal {P})$
gives us a collection of s vertex-disjoint cycles that cover
![]() $V(G)$
, where s is the number of connected components in
$V(G)$
, where s is the number of connected components in
![]() $S(\mathcal {P})$
. So in later sections we will be interested in obtaining balanced partitions
$S(\mathcal {P})$
. So in later sections we will be interested in obtaining balanced partitions
![]() $\mathcal {P}$
where the number of connected components of
$\mathcal {P}$
where the number of connected components of
![]() $S(\mathcal {P})$
is ‘small’.
$S(\mathcal {P})$
is ‘small’.
We need the following theorem, which states that a robust outexpander with linear minimum degree contains a (directed) Hamilton cycle.
Theorem 4.2 ([Reference Kühn, Osthus and Treglown23]; see also [Reference Lo and Patel25])
Let
![]() $1/n \ll \nu \leq \tau \ll \gamma <1$
. Let G be a robust
$1/n \ll \nu \leq \tau \ll \gamma <1$
. Let G be a robust
![]() $(\nu ,\tau )$
-outexpander on n vertices with
$(\nu ,\tau )$
-outexpander on n vertices with
![]() $\delta ^{0}(G)\geq \gamma n$
. Then G contains a Hamilton cycle.
$\delta ^{0}(G)\geq \gamma n$
. Then G contains a Hamilton cycle.
The next lemma shows that, under the conditions of Lemma 4.1,
![]() $V_{i*} \cup V_{*i}$
can be covered either by vertex-disjoint paths from
$V_{i*} \cup V_{*i}$
can be covered either by vertex-disjoint paths from
![]() $V_{i*} \setminus V_{ii}$
to
$V_{i*} \setminus V_{ii}$
to
![]() $V_{*i} \setminus V_{ii}$
or by a cycle, and it is used inductively to prove Lemma 4.1.
$V_{*i} \setminus V_{ii}$
or by a cycle, and it is used inductively to prove Lemma 4.1.
Lemma 4.3. Let
![]() $1/m \ll \nu \leq \tau \ll \alpha <1$
. Let G be a digraph with a vertex partition
$1/m \ll \nu \leq \tau \ll \alpha <1$
. Let G be a digraph with a vertex partition
![]() $\mathcal {P} = \{V_{ij} : i,j \in [k]\}$
. Let
$\mathcal {P} = \{V_{ij} : i,j \in [k]\}$
. Let
![]() $i \in [k]$
. Suppose that
$i \in [k]$
. Suppose that
![]() $G[V_{i*},V_{*i}]$
is a bipartite robust
$G[V_{i*},V_{*i}]$
is a bipartite robust
![]() $(\nu , \tau )$
-expander with bipartition
$(\nu , \tau )$
-expander with bipartition
![]() $V_{i*},V_{*i}$
such that
$V_{i*},V_{*i}$
such that
![]() $|V_{i*}| = |V_{*i}| = m $
and
$|V_{i*}| = |V_{*i}| = m $
and
![]() $\delta ( G[V_{i*},V_{*i}] ) \ge \alpha m$
. Let
$\delta ( G[V_{i*},V_{*i}] ) \ge \alpha m$
. Let
![]() $\phi : V_{i*} \setminus V_{ii} \rightarrow V_{*i} \setminus V_{ii}$
be a bijection. Then there exists a path system
$\phi : V_{i*} \setminus V_{ii} \rightarrow V_{*i} \setminus V_{ii}$
be a bijection. Then there exists a path system
![]() $\mathcal {Q}$
in
$\mathcal {Q}$
in
![]() $G_{ii}$
such that
$G_{ii}$
such that
![]() $\mathcal {Q} \cup \{\phi (v)v : v \in V_{i*} \setminus V_{ii} \}$
is a cycle with vertex set
$\mathcal {Q} \cup \{\phi (v)v : v \in V_{i*} \setminus V_{ii} \}$
is a cycle with vertex set
![]() $V_{i*} \cup V_{*i}$
. In the special case that
$V_{i*} \cup V_{*i}$
. In the special case that
![]() $V_{i*} = V_{*i} = V_{ii}$
, we have that
$V_{i*} = V_{*i} = V_{ii}$
, we have that
![]() $\phi $
is an empty function and
$\phi $
is an empty function and
![]() $\mathcal {Q}$
is a cycle (rather than a path system) with vertex set
$\mathcal {Q}$
is a cycle (rather than a path system) with vertex set
![]() $V_{ii}$
.
$V_{ii}$
.
Proof. Let H be the digraph on
![]() $V_{i*}$
obtained from
$V_{i*}$
obtained from
![]() $G_{ii}$
by identifying v with
$G_{ii}$
by identifying v with
![]() $\phi (v)$
for all
$\phi (v)$
for all
![]() $v \in V_{i*} \setminus V_{ii}$
and deleting any loops. Note that
$v \in V_{i*} \setminus V_{ii}$
and deleting any loops. Note that
![]() $\delta ^0(H) \ge \delta ( G[V_{i*},V_{*i}] ) - 1 \ge \alpha m /2$
and H is a robust
$\delta ^0(H) \ge \delta ( G[V_{i*},V_{*i}] ) - 1 \ge \alpha m /2$
and H is a robust
![]() $(\nu /2, 2\tau )$
-outexpander by Proposition 3.4 applied to the undirected bipartite graph
$(\nu /2, 2\tau )$
-outexpander by Proposition 3.4 applied to the undirected bipartite graph
![]() $G[V_{i*},V_{*i}]$
. By Theorem 4.2, H has a Hamilton cycle C. Note that if
$G[V_{i*},V_{*i}]$
. By Theorem 4.2, H has a Hamilton cycle C. Note that if
![]() $V_{i*}=V_{ii}=V_{*i}$
, then H coincides with
$V_{i*}=V_{ii}=V_{*i}$
, then H coincides with
![]() $G[V_{ii}]$
, proving the lemma in this case. If not, let
$G[V_{ii}]$
, proving the lemma in this case. If not, let
![]() $V_{i*}\setminus V_{ii} = \{ x_1, \dots , x_{\ell }\}$
be such that C visits
$V_{i*}\setminus V_{ii} = \{ x_1, \dots , x_{\ell }\}$
be such that C visits
![]() $x_1, \ldots , x_{\ell }$
in that order. Thus, C can be decomposed into paths
$x_1, \ldots , x_{\ell }$
in that order. Thus, C can be decomposed into paths
![]() $P_1, \dots , P_{\ell }$
such that
$P_1, \dots , P_{\ell }$
such that
![]() $P_j$
is a path from
$P_j$
is a path from
![]() $x_j$
to
$x_j$
to
![]() $x_{j+1}$
, where we take
$x_{j+1}$
, where we take
![]() $x_{\ell +1} = x_1$
. Let
$x_{\ell +1} = x_1$
. Let
![]() $Q_j$
be obtained from
$Q_j$
be obtained from
![]() $P_j$
by replacing
$P_j$
by replacing
![]() $x_{j+1}$
with
$x_{j+1}$
with
![]() $\phi (x_{j+1})$
. Note that
$\phi (x_{j+1})$
. Note that
![]() $Q_j$
is a path in
$Q_j$
is a path in
![]() $G_{ii}$
from
$G_{ii}$
from
![]() $x_j$
to
$x_j$
to
![]() $\phi (x_{j+1})$
. The result follows by setting
$\phi (x_{j+1})$
. The result follows by setting
![]() $\mathcal {Q} = \{Q_1, \ldots , Q_{\ell }\}$
.
$\mathcal {Q} = \{Q_1, \ldots , Q_{\ell }\}$
.
We now prove Lemma 4.1. For a connected component I in
![]() $S(\mathcal {P})$
, the idea is to apply Lemma 4.3 to each
$S(\mathcal {P})$
, the idea is to apply Lemma 4.3 to each
![]() $i \in I$
. Some care is needed to ensure that the union of path systems forms only one cycle.
$i \in I$
. Some care is needed to ensure that the union of path systems forms only one cycle.
Proof of Lemma 4.1
If I consists of a single vertex say i, then the result follows by Lemma 4.3 (since in that case
![]() $V_{i*} = V_{*i} = V_{ii}$
). Now assume
$V_{i*} = V_{*i} = V_{ii}$
). Now assume
![]() $|I|\geq 2$
, so
$|I|\geq 2$
, so
![]() $V_{i*}\cup V_{*i}\neq V_{ii}$
for all
$V_{i*}\cup V_{*i}\neq V_{ii}$
for all
![]() $i\in I$
. Without loss of generality, let
$i\in I$
. Without loss of generality, let
![]() $I = [\ell ]$
and order the indices of I such that for each
$I = [\ell ]$
and order the indices of I such that for each
![]() $j \in [\ell -1]$
, there is a
$j \in [\ell -1]$
, there is a
![]() $j' \in [\ell ] \setminus [j]$
with
$j' \in [\ell ] \setminus [j]$
with
![]() $j j' \in E(S(\mathcal {P}))$
. This can be achieved since I is connected, (e.g., by taking a reverse breadth-first search ordering). Note that
$j j' \in E(S(\mathcal {P}))$
. This can be achieved since I is connected, (e.g., by taking a reverse breadth-first search ordering). Note that
![]() $V_{ij}=V_{ji}=\emptyset $
for all
$V_{ij}=V_{ji}=\emptyset $
for all
![]() $i\in [\ell ]$
and
$i\in [\ell ]$
and
![]() $j\notin [\ell ]$
.
$j\notin [\ell ]$
.
For
![]() $i\in [\ell ]$
, let
$i\in [\ell ]$
, let
![]() $W^+_i=\bigcup _{i'\in [i],\, j'\notin [i]}V_{i'j'} = \bigcup _{i' \in [i]}V_{i'*} \setminus \bigcup _{i',j'\in [i]}V_{i'j'}$
and
$W^+_i=\bigcup _{i'\in [i],\, j'\notin [i]}V_{i'j'} = \bigcup _{i' \in [i]}V_{i'*} \setminus \bigcup _{i',j'\in [i]}V_{i'j'}$
and
![]() $W^-_i=\bigcup _{i'\notin [i],\, j'\in [i]}V_{i'j'} = \bigcup _{j' \in [i]}V_{*j'} \setminus \bigcup _{i',j'\in [i]}V_{i'j'}$
. Since
$W^-_i=\bigcup _{i'\notin [i],\, j'\in [i]}V_{i'j'} = \bigcup _{j' \in [i]}V_{*j'} \setminus \bigcup _{i',j'\in [i]}V_{i'j'}$
. Since
![]() $\mathcal {P}$
is balanced,
$\mathcal {P}$
is balanced,
![]() $|W^+_i| = |W^-_i|$
for each
$|W^+_i| = |W^-_i|$
for each
![]() $i \in [\ell ]$
. Also, by our ordering of the indices, we have that
$i \in [\ell ]$
. Also, by our ordering of the indices, we have that
![]() $W_i^+,W_i^-\neq \emptyset $
for
$W_i^+,W_i^-\neq \emptyset $
for
![]() $i\in [\ell -1]$
and that
$i\in [\ell -1]$
and that
![]() $W_{\ell }^+=W_{\ell }^-= \emptyset $
.
$W_{\ell }^+=W_{\ell }^-= \emptyset $
.
Let
![]() $\mathcal {Q}_0=W_0^+=W_0^-=\emptyset $
and suppose for some
$\mathcal {Q}_0=W_0^+=W_0^-=\emptyset $
and suppose for some
![]() $i \in [\ell ]$
, we have already found a path system
$i \in [\ell ]$
, we have already found a path system
![]() $\mathcal {Q}_{i-1}$
such that
$\mathcal {Q}_{i-1}$
such that
![]() $V(\mathcal {Q}_{i-1}) = \bigcup _{i' \in [i-1]} \left ( V_{i'*} \cup V_{*i'} \right )$
and
$V(\mathcal {Q}_{i-1}) = \bigcup _{i' \in [i-1]} \left ( V_{i'*} \cup V_{*i'} \right )$
and
![]() $\mathcal {Q}_{i-1}$
consists of precisely
$\mathcal {Q}_{i-1}$
consists of precisely
![]() $|W^+_{i-1}|$
paths from
$|W^+_{i-1}|$
paths from
![]() $W^+_{i-1}$
to
$W^+_{i-1}$
to
![]() $W^-_{i-1}$
. We now construct
$W^-_{i-1}$
. We now construct
![]() $\mathcal {Q}_{i}$
as follows. Let
$\mathcal {Q}_{i}$
as follows. Let
![]() $\phi : V_{i*} \setminus V_{ii} \rightarrow V_{*i} \setminus V_{ii} $
be any bijection such that if there is a path in
$\phi : V_{i*} \setminus V_{ii} \rightarrow V_{*i} \setminus V_{ii} $
be any bijection such that if there is a path in
![]() $\mathcal {Q}_{i-1}$
from
$\mathcal {Q}_{i-1}$
from
![]() $v_+ \in V_{*i}\setminus V_{ii}$
to
$v_+ \in V_{*i}\setminus V_{ii}$
to
![]() $v_- \in V_{i*}\setminus V_{ii}$
, then
$v_- \in V_{i*}\setminus V_{ii}$
, then
![]() $\phi (v_-) = v_+ $
. Apply Lemma 4.3 and obtain a path system
$\phi (v_-) = v_+ $
. Apply Lemma 4.3 and obtain a path system
![]() $\mathcal {Q}_i'$
in
$\mathcal {Q}_i'$
in
![]() $G_{ii}$
such that
$G_{ii}$
such that
![]() $\mathcal {Q}_i' \cup \{\phi (v)v : v \in V_{i*}\setminus V_{ii}\}$
is a cycle with vertex set
$\mathcal {Q}_i' \cup \{\phi (v)v : v \in V_{i*}\setminus V_{ii}\}$
is a cycle with vertex set
![]() $V_{i*} \cup V_{*i}$
. We set
$V_{i*} \cup V_{*i}$
. We set
![]() $\mathcal {Q}_{i} = \mathcal {Q}_{i-1} \cup \mathcal {Q}_i'$
.
$\mathcal {Q}_{i} = \mathcal {Q}_{i-1} \cup \mathcal {Q}_i'$
.
Suppose
![]() $i = \ell $
. Note that
$i = \ell $
. Note that
![]() $W^-_{\ell -1} = V_{\ell *} \setminus V_{\ell \ell }$
and
$W^-_{\ell -1} = V_{\ell *} \setminus V_{\ell \ell }$
and
![]() $W^+_{\ell -1} = V_{*\ell } \setminus V_{\ell \ell }$
. Hence
$W^+_{\ell -1} = V_{*\ell } \setminus V_{\ell \ell }$
. Hence
![]() $\mathcal {Q}_{\ell -1}$
consists of paths from
$\mathcal {Q}_{\ell -1}$
consists of paths from
![]() $\phi (v) \in W_{\ell -1}^+$
to
$\phi (v) \in W_{\ell -1}^+$
to
![]() $v \in W_{\ell -1}^-$
, we have
$v \in W_{\ell -1}^-$
, we have
![]() $V(\mathcal {Q}_{\ell -1}) = \bigcup _{i' \in [\ell -1]} \left ( V_{i'*} \cup V_{*i'} \right )= \bigcup _{i' \in [\ell ]} \left ( V_{i'*} \cup V_{*i'} \right ) \setminus V_{\ell \ell }$
. Since
$V(\mathcal {Q}_{\ell -1}) = \bigcup _{i' \in [\ell -1]} \left ( V_{i'*} \cup V_{*i'} \right )= \bigcup _{i' \in [\ell ]} \left ( V_{i'*} \cup V_{*i'} \right ) \setminus V_{\ell \ell }$
. Since
![]() $\mathcal {Q}_{\ell }' \cup \{\phi (v)v : v \in V_{\ell *} \setminus V_{\ell \ell }\}$
is a cycle with vertex set
$\mathcal {Q}_{\ell }' \cup \{\phi (v)v : v \in V_{\ell *} \setminus V_{\ell \ell }\}$
is a cycle with vertex set
![]() $V_{\ell *} \cup V_{* \ell }$
, we deduce that
$V_{\ell *} \cup V_{* \ell }$
, we deduce that
![]() $\mathcal {Q}_{\ell } = \mathcal {Q}_{\ell }' \cup \mathcal {Q}_{\ell -1}$
is a cycle with vertex set
$\mathcal {Q}_{\ell } = \mathcal {Q}_{\ell }' \cup \mathcal {Q}_{\ell -1}$
is a cycle with vertex set
![]() $\bigcup _{i' \in [\ell ]} \left ( V_{i'*} \cup V_{*i'} \right )$
as required.
$\bigcup _{i' \in [\ell ]} \left ( V_{i'*} \cup V_{*i'} \right )$
as required.
Suppose
![]() $i \in [\ell - 1]$
. Note that
$i \in [\ell - 1]$
. Note that
![]() $V(\mathcal {Q}_{i}) = \bigcup _{i' \in [i]} \left ( V_{i'*} \cup V_{*i'} \right )$
. It remains to check that
$V(\mathcal {Q}_{i}) = \bigcup _{i' \in [i]} \left ( V_{i'*} \cup V_{*i'} \right )$
. It remains to check that
![]() $\mathcal {Q}_i$
is a path system consisting of precisely
$\mathcal {Q}_i$
is a path system consisting of precisely
![]() $|W_i^+|$
paths from
$|W_i^+|$
paths from
![]() $W_i^+$
to
$W_i^+$
to
![]() $W_i^-$
. Note first that paths in
$W_i^-$
. Note first that paths in
![]() $\mathcal {Q}^{\prime }_i \subseteq G_{ii}$
start in
$\mathcal {Q}^{\prime }_i \subseteq G_{ii}$
start in
![]() $V_{i*} \setminus V_{ii}$
and end in
$V_{i*} \setminus V_{ii}$
and end in
![]() $V_{*i} \setminus V_{ii}$
and have all internal vertices in
$V_{*i} \setminus V_{ii}$
and have all internal vertices in
![]() $V_{ii}$
. On the other hand a path in
$V_{ii}$
. On the other hand a path in
![]() $\mathcal {Q}_{i-1}$
can only intersect
$\mathcal {Q}_{i-1}$
can only intersect
![]() $V_{*i}$
at its start point and
$V_{*i}$
at its start point and
![]() $V_{i*}$
at its end point and it avoids
$V_{i*}$
at its end point and it avoids
![]() $V_{ii}$
. Therefore in
$V_{ii}$
. Therefore in
![]() $\mathcal {Q}_{i} = \mathcal {Q}_{i-1} \cup \mathcal {Q}^{\prime }_i$
, all indegrees and outdegrees are at most
$\mathcal {Q}_{i} = \mathcal {Q}_{i-1} \cup \mathcal {Q}^{\prime }_i$
, all indegrees and outdegrees are at most
![]() $1$
. A vertex has indegree zero in
$1$
. A vertex has indegree zero in
![]() $\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
if and only if it is a start point of some path in
$\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
if and only if it is a start point of some path in
![]() $\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
but not an endpoint of any path in
$\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
but not an endpoint of any path in
![]() $\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
, (i.e., the set of vertices of indegree zero is
$\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
, (i.e., the set of vertices of indegree zero is
and similarly the set of vertices of outdegree zero is
![]() $W_i^-$
. Finally it remains to check that there are no cycles in
$W_i^-$
. Finally it remains to check that there are no cycles in
![]() $\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
. By our choice of
$\mathcal {Q}_{i-1}\cup \mathcal {Q}_i'$
. By our choice of
![]() $\phi $
, if there is a cycle, it spans all the vertices of
$\phi $
, if there is a cycle, it spans all the vertices of
![]() $V(\mathcal {Q}_{i-1}\cup \mathcal {Q}_i')$
, but this cannot happen because vertices in
$V(\mathcal {Q}_{i-1}\cup \mathcal {Q}_i')$
, but this cannot happen because vertices in
![]() $W_i^+\neq \emptyset $
have in-degree zero.
$W_i^+\neq \emptyset $
have in-degree zero.
5. Balanced path systems and path contraction
As mentioned in the previous section, in order to apply Lemma 4.1 to obtain a suitable cycle partition of a dense regular digraph G, we will require a vertex partition
![]() $\mathcal {P}$
of G such as that given by Theorem 3.5 but with the additional properties that
$\mathcal {P}$
of G such as that given by Theorem 3.5 but with the additional properties that
![]() $\mathcal {P}$
is balanced and
$\mathcal {P}$
is balanced and
![]() $S(\mathcal {P})$
has few connected components. In this section, we state a result (Lemma 5.4) that allows us to adjust a partition
$S(\mathcal {P})$
has few connected components. In this section, we state a result (Lemma 5.4) that allows us to adjust a partition
![]() $\mathcal {P}$
to have these additional properties. In particular, if
$\mathcal {P}$
to have these additional properties. In particular, if
![]() $\mathcal {P}$
is not balanced, Lemma 5.4 guarantees us a so-called
$\mathcal {P}$
is not balanced, Lemma 5.4 guarantees us a so-called
![]() $\mathcal {P}$
-balanced path system in G whose ‘contraction’ makes
$\mathcal {P}$
-balanced path system in G whose ‘contraction’ makes
![]() $\mathcal {P}$
balanced in a suitable way. At the end of the section we show how Lemma 5.4 implies our main result, Theorem 1.3.
$\mathcal {P}$
balanced in a suitable way. At the end of the section we show how Lemma 5.4 implies our main result, Theorem 1.3.
Let
![]() $\mathcal {P} =\{V_{ij}:i,j \in [k]\}$
be a partition of a vertex set V and let G be a digraph on V. Recall the definition of
$\mathcal {P} =\{V_{ij}:i,j \in [k]\}$
be a partition of a vertex set V and let G be a digraph on V. Recall the definition of
![]() $G_{ij}$
and of P being balanced at the beginning of Section 4. Write
$G_{ij}$
and of P being balanced at the beginning of Section 4. Write
![]() $G_{i*} = \bigcup _{j\neq i} G_{ij}$
and
$G_{i*} = \bigcup _{j\neq i} G_{ij}$
and
![]() $G_{*j} = \bigcup _{i \ne j} G_{ij}$
. Let
$G_{*j} = \bigcup _{i \ne j} G_{ij}$
. Let
![]() $\mathcal {B}(G, \mathcal {P}) = G - \bigcup _{i \in [k]} G_{ii}$
. Note that
$\mathcal {B}(G, \mathcal {P}) = G - \bigcup _{i \in [k]} G_{ii}$
. Note that
![]() $\mathcal {B}(G, \mathcal {P}) = \bigcup _{i \in [k]} G_{i*} = \bigcup _{j \in [k]} G_{*j}$
. We say that a digraph H on V (where H is usually a path system in G) is
$\mathcal {B}(G, \mathcal {P}) = \bigcup _{i \in [k]} G_{i*} = \bigcup _{j \in [k]} G_{*j}$
. We say that a digraph H on V (where H is usually a path system in G) is
![]() $\mathcal {P}$
-balanced if, for all
$\mathcal {P}$
-balanced if, for all
![]() $i \in [k]$
,
$i \in [k]$
,
 $$ \begin{align*} |V_{i*}|-|V_{*i}| = e_H(V_{i*},V) - e_H(V,V_{*i}) = \sum_{j \in [k]} e(H_{ij}) - \sum_{j \in [k]} e(H_{ji}) = e(H_{i*}) - e(H_{*i}). \end{align*} $$
$$ \begin{align*} |V_{i*}|-|V_{*i}| = e_H(V_{i*},V) - e_H(V,V_{*i}) = \sum_{j \in [k]} e(H_{ij}) - \sum_{j \in [k]} e(H_{ji}) = e(H_{i*}) - e(H_{*i}). \end{align*} $$
The above gives three equivalent conditions for H to be
![]() $\mathcal {P}$
-balanced. Note that if H is regular, then it is
$\mathcal {P}$
-balanced. Note that if H is regular, then it is
![]() $\mathcal {P}$
-balanced for any
$\mathcal {P}$
-balanced for any
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Let Q be a path in G from
![]() $v_+ \in V_{i_+j_+}$
to
$v_+ \in V_{i_+j_+}$
to
![]() $v_- \in V_{i_-j_-}$
. We define the Q-contracted subgraph
$v_- \in V_{i_-j_-}$
. We define the Q-contracted subgraph
![]() $G'$
of G to be
$G'$
of G to be
![]() $G \setminus V(Q)$
together with a new vertex w such that
$G \setminus V(Q)$
together with a new vertex w such that
![]() $N^+_{G'}(w) = N^+_G(v_-) \setminus V(Q)$
and
$N^+_{G'}(w) = N^+_G(v_-) \setminus V(Q)$
and
![]() $N^-_{G'}(w) = N^-_G(v_+) \setminus V(Q)$
. We call
$N^-_{G'}(w) = N^-_G(v_+) \setminus V(Q)$
. We call
![]() $\mathcal {P}'=\{V_{ij}':i,j \in [k]\}$
the Q-contracted partition of
$\mathcal {P}'=\{V_{ij}':i,j \in [k]\}$
the Q-contracted partition of
![]() $\mathcal {P}$
, where
$\mathcal {P}$
, where
 $$ \begin{align} V_{ij}' = \begin{cases} ( V_{ij} \setminus V(Q) ) \cup \{w\} & \text{if }(i,j) = (i_-,j_+);\\ V_{ij} \setminus V(Q) &\text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} V_{ij}' = \begin{cases} ( V_{ij} \setminus V(Q) ) \cup \{w\} & \text{if }(i,j) = (i_-,j_+);\\ V_{ij} \setminus V(Q) &\text{otherwise}. \end{cases} \end{align} $$
Let
![]() $\mathcal {Q}$
be a path system in G. The
$\mathcal {Q}$
be a path system in G. The
![]() $\mathcal {Q}$
-contracted subgraph of G (and
$\mathcal {Q}$
-contracted subgraph of G (and
![]() $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
![]() $\mathcal {P}$
) is obtained by successively contracting each
$\mathcal {P}$
) is obtained by successively contracting each
![]() $Q \in \mathcal {Q}$
for G (and
$Q \in \mathcal {Q}$
for G (and
![]() $\mathcal {P}$
, respectively).
$\mathcal {P}$
, respectively).
The following two propositions follow from the definition of
![]() $\mathcal {Q}$
-contraction. In fact the definitions are chosen precisely so that these propositions hold.
$\mathcal {Q}$
-contraction. In fact the definitions are chosen precisely so that these propositions hold.
Proposition 5.1. Let G be a digraph and
![]() $\mathcal {Q}$
be a path system in G. Suppose that the
$\mathcal {Q}$
be a path system in G. Suppose that the
![]() $\mathcal {Q}$
-contracted subgraph of G contains a
$\mathcal {Q}$
-contracted subgraph of G contains a
![]() $1$
-factor with
$1$
-factor with
![]() $\ell $
cycles. Then G also contains a
$\ell $
cycles. Then G also contains a
![]() $1$
-factor containing
$1$
-factor containing
![]() $\mathcal {Q}$
with
$\mathcal {Q}$
with
![]() $\ell $
cycles. (The new
$\ell $
cycles. (The new
![]() $1$
-factor is simply the old
$1$
-factor is simply the old
![]() $1$
-factor with the paths in
$1$
-factor with the paths in
![]() $\mathcal {Q}$
uncontracted.)
$\mathcal {Q}$
uncontracted.)
Proposition 5.2. Let G be a digraph on n vertices and let
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G)$
. Let
$V(G)$
. Let
![]() $\mathcal {Q}$
be a path system in G such that
$\mathcal {Q}$
be a path system in G such that
![]() $e(\mathcal {Q}) < |V_{i*}|, |V_{*i}|$
for all
$e(\mathcal {Q}) < |V_{i*}|, |V_{*i}|$
for all
![]() $i \in [k]$
. Let
$i \in [k]$
. Let
![]() $G'$
and
$G'$
and
![]() $\mathcal {P}' = \{ V^{\prime }_{ij} : i,j \in [k]\}$
be the
$\mathcal {P}' = \{ V^{\prime }_{ij} : i,j \in [k]\}$
be the
![]() $\mathcal {Q}$
-contracted subgraph of G and
$\mathcal {Q}$
-contracted subgraph of G and
![]() $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
![]() $\mathcal {P}$
, respectively. Then for all
$\mathcal {P}$
, respectively. Then for all
![]() $i \in [k]$
,
$i \in [k]$
,
![]() $\delta (G'[V^{\prime }_{i*},V^{\prime }_{*i}] )\geq \delta (G[V_{i*},V_{*i}] ) - 2 e(\mathcal {Q})$
.Footnote 4
$\delta (G'[V^{\prime }_{i*},V^{\prime }_{*i}] )\geq \delta (G[V_{i*},V_{*i}] ) - 2 e(\mathcal {Q})$
.Footnote 4
Proposition 5.3. Let
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of a vertex set V and
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of a vertex set V and
![]() $\mathcal {Q}$
be a
$\mathcal {Q}$
be a
![]() $\mathcal {P}$
-balanced path system on V. Then the
$\mathcal {P}$
-balanced path system on V. Then the
![]() $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
![]() $\mathcal {P}$
is balanced.
$\mathcal {P}$
is balanced.
Proof. Let
![]() $Q \in \mathcal {Q}$
be a path from
$Q \in \mathcal {Q}$
be a path from
![]() $v_+ \in V_{i_+j_+}$
to
$v_+ \in V_{i_+j_+}$
to
![]() $v_- \in V_{i_-j_-}$
. For each
$v_- \in V_{i_-j_-}$
. For each
![]() $i,j \in [k]$
, let
$i,j \in [k]$
, let
![]() $q_{ij} = e(Q_{ij})$
(i.e., the number of edges of Q from
$q_{ij} = e(Q_{ij})$
(i.e., the number of edges of Q from
![]() $V_{i*}$
to
$V_{i*}$
to
![]() $V_{*j}$
.) Let
$V_{*j}$
.) Let
![]() $\mathcal {P}' = \{ V_{ij}' : i,j \in [k] \} $
be the Q-contracted partition of
$\mathcal {P}' = \{ V_{ij}' : i,j \in [k] \} $
be the Q-contracted partition of
![]() $\mathcal {P}$
. Consider
$\mathcal {P}$
. Consider
![]() $i \in [k]$
. Note that
$i \in [k]$
. Note that

Therefore,
![]() $|V^{\prime }_{i*}| - |V^{\prime }_{*i}| = |V_{i*}| - |V_{*i}| - \sum _{j \in [k]} (q_{ij} - q_{ji}) = |V_{i*}| - |V_{*i}| - ( e(Q_{i*}) - e(Q_{*i}) )$
. A similar statement holds for the
$|V^{\prime }_{i*}| - |V^{\prime }_{*i}| = |V_{i*}| - |V_{*i}| - \sum _{j \in [k]} (q_{ij} - q_{ji}) = |V_{i*}| - |V_{*i}| - ( e(Q_{i*}) - e(Q_{*i}) )$
. A similar statement holds for the
![]() $\mathcal {Q}$
-contracted partition
$\mathcal {Q}$
-contracted partition
![]() $\mathcal {P}^* = \{ V_{ij}^* : i,j \in [k] \}$
of
$\mathcal {P}^* = \{ V_{ij}^* : i,j \in [k] \}$
of
![]() $\mathcal {P}$
, and the result follows as
$\mathcal {P}$
, and the result follows as
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathcal {P}$
-balanced (i.e., for each
$\mathcal {P}$
-balanced (i.e., for each
![]() $i \in [k]$
,
$i \in [k]$
,
![]() $ |V^*_{i*}| - |V^*_{*i}|=|V_{i*}| - |V_{*i}| - ( e(\mathcal {Q}_{i*}) - e(\mathcal {Q}_{*i}) )=0$
).
$ |V^*_{i*}| - |V^*_{*i}|=|V_{i*}| - |V_{*i}| - ( e(\mathcal {Q}_{i*}) - e(\mathcal {Q}_{*i}) )=0$
).
The next lemma says that one can adjust the vertex partition
![]() $\mathcal {P}$
found in Theorem 3.5 by a small amount, and find a
$\mathcal {P}$
found in Theorem 3.5 by a small amount, and find a
![]() $\mathcal {P}$
-balanced path system
$\mathcal {P}$
-balanced path system
![]() $\mathcal {Q}$
such that
$\mathcal {Q}$
such that
![]() $S(\mathcal {P}^*)$
has few connected components, where
$S(\mathcal {P}^*)$
has few connected components, where
![]() $\mathcal {P}^*$
is the
$\mathcal {P}^*$
is the
![]() $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
![]() $\mathcal {P}$
. It is exactly what we need to prove Theorem 1.3, as we shall see. In Section 6, we break this lemma down into two further lemmas.
$\mathcal {P}$
. It is exactly what we need to prove Theorem 1.3, as we shall see. In Section 6, we break this lemma down into two further lemmas.
Lemma 5.4. Let
![]() $1/n \ll \gamma \ll \alpha , 1/k$
. Let G be a d-regular digraph on n vertices with
$1/n \ll \gamma \ll \alpha , 1/k$
. Let G be a d-regular digraph on n vertices with
![]() $d \ge \alpha n$
and
$d \ge \alpha n$
and
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G)$
such that, for all
$V(G)$
such that, for all
![]() $i,j \in [k]$
,
$i,j \in [k]$
,
-
(i)
 $\delta ( G [ V_{i*},V_{*i} ] ) \ge d/k$
;
$\delta ( G [ V_{i*},V_{*i} ] ) \ge d/k$
; -
(ii)
 $\left | |V_{i*}| - |V_{*i}| \right | \le \gamma n$
;
$\left | |V_{i*}| - |V_{*i}| \right | \le \gamma n$
; -
(iii)
 $ |V_{i*}|, |V_{*i}| \ge d - \gamma n $
;
$ |V_{i*}|, |V_{*i}| \ge d - \gamma n $
; -
(iv) all but at most
 $\gamma n $
vertices
$\gamma n $
vertices
 $x \in V_{ij}$
satisfy
$x \in V_{ij}$
satisfy
 $d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
.
$d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
.
Then there exists a partition
![]() $\mathcal {P}' = \{ V^{\prime }_{ij} : i,j \in [k]\}$
of
$\mathcal {P}' = \{ V^{\prime }_{ij} : i,j \in [k]\}$
of
![]() $V(G)$
and a
$V(G)$
and a
![]() $\mathcal {P}'$
-balanced path system
$\mathcal {P}'$
-balanced path system
![]() $\mathcal {Q}$
in G such that
$\mathcal {Q}$
in G such that
-
(a) for all
 $i, j \in [k]$
,
$i, j \in [k]$
,
 $| V_{ij} \triangle V^{\prime }_{ij}| \le \gamma ^{1/2} n$
;
$| V_{ij} \triangle V^{\prime }_{ij}| \le \gamma ^{1/2} n$
; -
(b) for all
 $i \in [k], \delta (G[V_{i*}', V_{*i}']) \geq (d/k) - \gamma ^{1/2}n$
;
$i \in [k], \delta (G[V_{i*}', V_{*i}']) \geq (d/k) - \gamma ^{1/2}n$
; -
(c)
 $ e(\mathcal {Q}) \le \gamma ^{1/2} n$
;
$ e(\mathcal {Q}) \le \gamma ^{1/2} n$
; -
(d)
 $S(\mathcal {P}^*)$
has at most
$S(\mathcal {P}^*)$
has at most
 $n/(qd+1)$
connected components, where
$n/(qd+1)$
connected components, where
 $\mathcal {P}^*$
is the
$\mathcal {P}^*$
is the
 $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
 $\mathcal {P}'$
, and we set
$\mathcal {P}'$
, and we set
 $q = 2$
if G is an oriented graph and
$q = 2$
if G is an oriented graph and
 $q=1$
otherwise.
$q=1$
otherwise.
5.1. Proof of Theorem 1.3
We now prove Theorem 1.3 assuming Lemma 5.4.
Proof of Theorem 1.3
Choose a non-decreasing function
![]() $g : (0, 1) \rightarrow (0, 1)$
such that the requirements of Lemmas 4.1 (with
$g : (0, 1) \rightarrow (0, 1)$
such that the requirements of Lemmas 4.1 (with
![]() $m = \alpha n/2$
) and 5.4 are satisfied whenever
$m = \alpha n/2$
) and 5.4 are satisfied whenever
![]() $n, \gamma , \nu , \tau , \alpha $
satisfy
$n, \gamma , \nu , \tau , \alpha $
satisfy
where we write
![]() $a \ll _g b$
to mean
$a \ll _g b$
to mean
![]() $a \leq g(b)$
. Set
$a \leq g(b)$
. Set
![]() $f(x) := \min (x, g(x^2/4))$
. Fix
$f(x) := \min (x, g(x^2/4))$
. Fix
![]() $\tau \leq f(\alpha )$
and apply Theorem 3.5 to obtain
$\tau \leq f(\alpha )$
and apply Theorem 3.5 to obtain
![]() $n_0$
such that for any d-regular digraph G on
$n_0$
such that for any d-regular digraph G on
![]() $n \geq n_0$
vertices with
$n \geq n_0$
vertices with
![]() $d \ge \alpha n $
, there exists
$d \ge \alpha n $
, there exists
![]() $\gamma $
and
$\gamma $
and
![]() $\nu $
such that
$\nu $
such that
and a partition
![]() $\mathcal {P} = \{ V_{ij}: i,j \in [k]\}$
of
$\mathcal {P} = \{ V_{ij}: i,j \in [k]\}$
of
![]() $V(G)$
satisfying, for all
$V(G)$
satisfying, for all
![]() $i,j \in [k]$
,
$i,j \in [k]$
,
-
(a1)
 $G[V_{i*},V_{*i}]$
is a bipartite robust
$G[V_{i*},V_{*i}]$
is a bipartite robust
 $(\nu , \tau )$
-expander with partition
$(\nu , \tau )$
-expander with partition
 $V_{i*},V_{*i}$
;
$V_{i*},V_{*i}$
; -
(a2) for all
 $x \in V_{ij}$
and
$x \in V_{ij}$
and
 $i',j' \in [k]$
,
$i',j' \in [k]$
,
 $d^+(x, V_{*i}) \ge d^+(x, V_{*i'})$
and
$d^+(x, V_{*i}) \ge d^+(x, V_{*i'})$
and
 $d^-(x, V_{j*}) \ge d^-(x, V_{j'*})$
, so in particular,
$d^-(x, V_{j*}) \ge d^-(x, V_{j'*})$
, so in particular,
 $\delta ( G [ V_{i*},V_{*i} ] ) \ge d/k$
;
$\delta ( G [ V_{i*},V_{*i} ] ) \ge d/k$
; -
(a3)
 $\left | |V_{i*}| - |V_{*i}| \right | \le \gamma n$
;
$\left | |V_{i*}| - |V_{*i}| \right | \le \gamma n$
; -
(a4) all but at most
 $\gamma n $
vertices
$\gamma n $
vertices
 $x \in V_{ij}$
satisfy
$x \in V_{ij}$
satisfy
 $d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
;
$d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
; -
(a5)
 $k \le n / (d-\gamma n)$
.
$k \le n / (d-\gamma n)$
.
Note that (
![]() $\mathrm{a}_5$
) in particular implies that
$\mathrm{a}_5$
) in particular implies that
![]() $\gamma \ll 1/k$
. Furthermore, (
$\gamma \ll 1/k$
. Furthermore, (
![]() $\mathrm{a}_2$
) and (
$\mathrm{a}_2$
) and (
![]() $\mathrm{a}_4$
) together with
$\mathrm{a}_4$
) together with
![]() $\gamma \ll 1/k$
imply that
$\gamma \ll 1/k$
imply that
-
(a6) for all
 $i \in [k]$
,
$i \in [k]$
,
 $|V_{i*}|,|V_{*i}|\ge d-\gamma n$
.
$|V_{i*}|,|V_{*i}|\ge d-\gamma n$
.
Let
![]() $q=2$
if G is oriented, and
$q=2$
if G is oriented, and
![]() $q=1$
otherwise. Apply Lemma 5.4 and obtain a partition
$q=1$
otherwise. Apply Lemma 5.4 and obtain a partition
![]() $\mathcal {P}' = \{ V^{\prime }_{ij} : i,j \in [k]\}$
of
$\mathcal {P}' = \{ V^{\prime }_{ij} : i,j \in [k]\}$
of
![]() $V(G)$
and a
$V(G)$
and a
![]() $\mathcal {P}'$
-balanced path system
$\mathcal {P}'$
-balanced path system
![]() $\mathcal {Q}$
in G such that
$\mathcal {Q}$
in G such that
-
(b1) for all
 $i, j \in [k]$
,
$i, j \in [k]$
,
 $| V_{ij} \triangle V^{\prime }_{ij}| \le \gamma ^{1/2} n$
;
$| V_{ij} \triangle V^{\prime }_{ij}| \le \gamma ^{1/2} n$
; -
(b2) for all
 $i \in [k], \delta (G[V_{i*}', V_{*i}']) \geq (d/k) - \gamma ^{1/2}n$
;
$i \in [k], \delta (G[V_{i*}', V_{*i}']) \geq (d/k) - \gamma ^{1/2}n$
; -
(b3)
 $ e(\mathcal {Q}) \le \gamma ^{1/2} n$
;
$ e(\mathcal {Q}) \le \gamma ^{1/2} n$
; -
(b4)
 $S(\mathcal {P}^*)$
has at most
$S(\mathcal {P}^*)$
has at most
 $n/(qd+1)$
connected components, where
$n/(qd+1)$
connected components, where
 $\mathcal {P}^*$
is the
$\mathcal {P}^*$
is the
 $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
 $\mathcal {P}'$
.
$\mathcal {P}'$
.
Let
![]() $\mathcal {P}^* = \{V^*_{ij}:i,j \in [k]\}$
and let
$\mathcal {P}^* = \{V^*_{ij}:i,j \in [k]\}$
and let
![]() $G^*$
be the
$G^*$
be the
![]() $\mathcal {Q}$
-contracted subgraph of G. We will check that, for all
$\mathcal {Q}$
-contracted subgraph of G. We will check that, for all
![]() $i, j \in [k]$
,
$i, j \in [k]$
,
-
(c1)
 $\mathcal {P}^*$
is balanced;
$\mathcal {P}^*$
is balanced; -
(c2)
 $| V_{ij} \triangle V^*_{ij}| \le 5 \gamma ^{1/2} n$
;
$| V_{ij} \triangle V^*_{ij}| \le 5 \gamma ^{1/2} n$
; -
(c3)
 $|V_{i*}^*|,|V_{*i}^*|\ge d- 6 k\gamma ^{1/2} n \ge d/2$
;
$|V_{i*}^*|,|V_{*i}^*|\ge d- 6 k\gamma ^{1/2} n \ge d/2$
; -
(c4)
 $G^*[V^*_{i*},V^*_{*i}]$
is a bipartite robust
$G^*[V^*_{i*},V^*_{*i}]$
is a bipartite robust
 $(\nu /2, 2\tau )$
-expander with bipartition
$(\nu /2, 2\tau )$
-expander with bipartition
 $V^*_{i*},V^*_{*i}$
;
$V^*_{i*},V^*_{*i}$
; -
(c5)
 $\delta ( G^*[V^*_{i*},V^*_{*i}] ) \ge \alpha ^2 |V^*_{i*}|/2$
.
$\delta ( G^*[V^*_{i*},V^*_{*i}] ) \ge \alpha ^2 |V^*_{i*}|/2$
.
Note that (
![]() $\mathrm{c}_1$
) holds by Proposition 5.3. Consider
$\mathrm{c}_1$
) holds by Proposition 5.3. Consider
![]() $i,j \in [k]$
. Note that
$i,j \in [k]$
. Note that
implying (
![]() $\mathrm{c}_2$
). Hence (
$\mathrm{c}_2$
). Hence (
![]() $\mathrm{c}_3$
) follows from (
$\mathrm{c}_3$
) follows from (
![]() $\mathrm{a}_6$
) and (
$\mathrm{a}_6$
) and (
![]() $\mathrm{c}_2$
) as
$\mathrm{c}_2$
) as
![]() $\gamma \ll \alpha ,1/k$
. By (
$\gamma \ll \alpha ,1/k$
. By (
![]() $\mathrm{a}_1$
), (
$\mathrm{a}_1$
), (
![]() $\mathrm{c}_2$
), (
$\mathrm{c}_2$
), (
![]() $\mathrm{c}_3$
), and
$\mathrm{c}_3$
), and
![]() $\gamma \ll \nu $
, Lemma 3.1 (applied to the bipartite graph
$\gamma \ll \nu $
, Lemma 3.1 (applied to the bipartite graph
![]() $G^*[V^*_{i*},V^*_{*i}]\cup G[V_{i*},V_{*i}]$
with
$G^*[V^*_{i*},V^*_{*i}]\cup G[V_{i*},V_{*i}]$
with
![]() $V_{i*}, V_{*i}, V^*_{i*}, V^*_{*i}$
playing the roles of
$V_{i*}, V_{*i}, V^*_{i*}, V^*_{*i}$
playing the roles of
![]() $A,B, A', B'$
respectively) implies that (
$A,B, A', B'$
respectively) implies that (
![]() $\mathrm{c}_4$
) holds. By (
$\mathrm{c}_4$
) holds. By (
![]() $a_6$
), (
$a_6$
), (
![]() $\mathrm{b}_1$
), and (
$\mathrm{b}_1$
), and (
![]() $\mathrm{b}_3$
), we have
$\mathrm{b}_3$
), we have
![]() $e(\mathcal {Q})\leq \gamma ^{1/2}n<d-\gamma n-k\gamma ^{1/2}n\leq |V^{\prime }_{i*}|,|V^{\prime }_{*i}|$
as
$e(\mathcal {Q})\leq \gamma ^{1/2}n<d-\gamma n-k\gamma ^{1/2}n\leq |V^{\prime }_{i*}|,|V^{\prime }_{*i}|$
as
![]() $\gamma \ll \alpha ,1/k$
. Hence, by Proposition 5.2,
$\gamma \ll \alpha ,1/k$
. Hence, by Proposition 5.2,
where the last inequality holds as
![]() $\gamma \ll \alpha , 1/k$
and
$\gamma \ll \alpha , 1/k$
and
![]() $k (\alpha - \gamma )\leq 1$
by (
$k (\alpha - \gamma )\leq 1$
by (
![]() $\mathrm{a}_5$
). Hence (
$\mathrm{a}_5$
). Hence (
![]() $\mathrm{c}_5$
) holds.
$\mathrm{c}_5$
) holds.
Apply Lemma 4.1 (with
![]() $G^*$
,
$G^*$
,
![]() $\mathcal {P}^*$
,
$\mathcal {P}^*$
,
![]() $d/2$
,
$d/2$
,
![]() $\nu /2$
,
$\nu /2$
,
![]() $2\tau $
,
$2\tau $
,
![]() $\alpha ^2/2$
playing the roles of G,
$\alpha ^2/2$
playing the roles of G,
![]() $\mathcal {P}$
, m,
$\mathcal {P}$
, m,
![]() $\nu $
,
$\nu $
,
![]() $\tau $
,
$\tau $
,
![]() $\alpha $
, respectively) to each connected component I in
$\alpha $
, respectively) to each connected component I in
![]() $S(\mathcal {P}^*)$
. Thus, by (
$S(\mathcal {P}^*)$
. Thus, by (
![]() $\mathrm{b}_4$
),
$\mathrm{b}_4$
),
![]() $G^*$
can be covered with at most
$G^*$
can be covered with at most
![]() $n/(qd + 1)$
vertex-disjoint cycles (where we have a cycle on
$n/(qd + 1)$
vertex-disjoint cycles (where we have a cycle on
![]() $\cup _{i \in I} (V_{i*} \cup V_{*i})$
for each component I of
$\cup _{i \in I} (V_{i*} \cup V_{*i})$
for each component I of
![]() $S(\mathcal {P}^*)$
so that each cycle has length at least
$S(\mathcal {P}^*)$
so that each cycle has length at least
![]() $d/2$
by (
$d/2$
by (
![]() $\mathrm{c}_3$
)). By Proposition 5.1, G can be covered with at most
$\mathrm{c}_3$
)). By Proposition 5.1, G can be covered with at most
![]() $n/(qd+1)$
vertex-disjoint cycles (each of length at least
$n/(qd+1)$
vertex-disjoint cycles (each of length at least
![]() $d/2$
).
$d/2$
).
6. Proof of Lemma 5.4
In the last section we reduced the task of proving Theorem 1.3 to the task of proving Lemma 5.4. In this section we reduce this further to the task of proving Lemmas 6.1 and 6.3. We start by introducing the notion of a non-trivial path system, which will help us control the number of connected components of
![]() $S(\mathcal {P}^*)$
(as required in the conclusion of Lemma 5.4).
$S(\mathcal {P}^*)$
(as required in the conclusion of Lemma 5.4).
Recall the definitions at the beginning of Sections 4 and 5. Let
![]() $\mathcal {P} =\{V_{ij}:i,j \in [k]\}$
be a partition of a vertex set V. We call a path system
$\mathcal {P} =\{V_{ij}:i,j \in [k]\}$
be a partition of a vertex set V. We call a path system
![]() $\mathcal {Q}$
on V non-trivial if there exists
$\mathcal {Q}$
on V non-trivial if there exists
![]() $i \ne j$
such that
$i \ne j$
such that
![]() $V_{ij} \setminus V(\mathcal {Q}) \ne \emptyset $
or
$V_{ij} \setminus V(\mathcal {Q}) \ne \emptyset $
or
![]() $\mathcal {Q}$
contains a path from
$\mathcal {Q}$
contains a path from
![]() $V_{*j}$
to
$V_{*j}$
to
![]() $V_{i*}$
. Otherwise, we call
$V_{i*}$
. Otherwise, we call
![]() $\mathcal {Q}$
a trivial path system. Note that if
$\mathcal {Q}$
a trivial path system. Note that if
![]() $\mathcal {Q}$
is non-trivial, then the
$\mathcal {Q}$
is non-trivial, then the
![]() $\mathcal {Q}$
-contracted partition
$\mathcal {Q}$
-contracted partition
![]() $\mathcal {P}'$
of
$\mathcal {P}'$
of
![]() $\mathcal {P}$
has the property that
$\mathcal {P}$
has the property that
![]() $S(\mathcal {P}')$
has at least one edge so that its number of connected components is strictly less than its number of vertices.
$S(\mathcal {P}')$
has at least one edge so that its number of connected components is strictly less than its number of vertices.
Lemma 6.1 below shows that, under the same hypothesis as Lemma 5.4, there exists a
![]() $\mathcal {P}$
-balanced path system with few edges, and moreover that this path system is non-trivial if further assumptions are made. We shall see at the end of the section that the existence of such a non-trivial
$\mathcal {P}$
-balanced path system with few edges, and moreover that this path system is non-trivial if further assumptions are made. We shall see at the end of the section that the existence of such a non-trivial
![]() $\mathcal {P}$
-balanced path system is enough to prove Lemma 5.4. In fact, a
$\mathcal {P}$
-balanced path system is enough to prove Lemma 5.4. In fact, a
![]() $\mathcal {P}$
-balanced path system alone (without the condition of being non-trivial) is enough to prove Lemma 5.4 except in the extremal cases when
$\mathcal {P}$
-balanced path system alone (without the condition of being non-trivial) is enough to prove Lemma 5.4 except in the extremal cases when
![]() $d \approx n/k$
if G is digraph and when
$d \approx n/k$
if G is digraph and when
![]() $d \approx n/ 2k$
if G is an oriented graph.
$d \approx n/ 2k$
if G is an oriented graph.
Lemma 6.1. Let
![]() $1/n \ll \gamma \ll 1/k, \alpha $
. Let
$1/n \ll \gamma \ll 1/k, \alpha $
. Let
![]() $G^0$
be a d-regular digraph on n vertices with
$G^0$
be a d-regular digraph on n vertices with
![]() $d \ge \alpha n$
and
$d \ge \alpha n$
and
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G^0)$
such that, for all
$V(G^0)$
such that, for all
![]() $i \in [k]$
,
$i \in [k]$
,
-
(i)
 $\delta ( G^0 [ V_{i*},V_{*i} ] ) \ge d/k$
;
$\delta ( G^0 [ V_{i*},V_{*i} ] ) \ge d/k$
; -
(ii)
 $\left | |V_{i*}| - |V_{*i}| \right | \le \gamma n$
;
$\left | |V_{i*}| - |V_{*i}| \right | \le \gamma n$
; -
(iii)
 $ |V_{i*}|, |V_{*i}| \ge d - \gamma n $
.
$ |V_{i*}|, |V_{*i}| \ge d - \gamma n $
.
Then
![]() $G^0$
contains a
$G^0$
contains a
![]() $\mathcal {P}$
-balanced path system
$\mathcal {P}$
-balanced path system
![]() $\mathcal {Q}$
such that
$\mathcal {Q}$
such that
![]() $e(\mathcal {Q}) \le k^2 \gamma n $
. Moreover, if one of the following holds
$e(\mathcal {Q}) \le k^2 \gamma n $
. Moreover, if one of the following holds
-
(m1)
 $\sum _{i,j \in [k] \colon i \ne j} |V_{ij}|> k^2\gamma n$
, or
$\sum _{i,j \in [k] \colon i \ne j} |V_{ij}|> k^2\gamma n$
, or -
(m2) there exists
 $v_0 \in V_{i_0j_0}$
for some
$v_0 \in V_{i_0j_0}$
for some
 $i_0 \ne j_0$
such that
$i_0 \ne j_0$
such that
 $d^{+}(v_0,V_{*i_0})-d^{-}(v_0,V_{i_0*})\ge 100 k^{12} \gamma ^{1/3}d$
,
$d^{+}(v_0,V_{*i_0})-d^{-}(v_0,V_{i_0*})\ge 100 k^{12} \gamma ^{1/3}d$
,
then we may assume that
![]() $\mathcal {Q}$
is non-trivial.
$\mathcal {Q}$
is non-trivial.
In case Lemma 5.4 gives a
![]() $\mathcal {P}$
-balanced but trivial path system (i.e., when both (m1) and (m2) fail), we use the next proposition to slightly modify
$\mathcal {P}$
-balanced but trivial path system (i.e., when both (m1) and (m2) fail), we use the next proposition to slightly modify
![]() $\mathcal {P}$
and Lemma 6.3 to find the desired non-trivial,
$\mathcal {P}$
and Lemma 6.3 to find the desired non-trivial,
![]() $\mathcal {P}$
-balanced path system.
$\mathcal {P}$
-balanced path system.
Proposition 6.2. Let
![]() $1/n \ll \gamma \ll 1/k, \alpha $
. Let
$1/n \ll \gamma \ll 1/k, \alpha $
. Let
![]() $G^0$
be a d-regular digraph on n vertices with
$G^0$
be a d-regular digraph on n vertices with
![]() $d \ge \alpha n$
and
$d \ge \alpha n$
and
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G^0)$
such that, for all distinct
$V(G^0)$
such that, for all distinct
![]() $i,j \in [k]$
,
$i,j \in [k]$
,
-
(i)
 $\delta ( G^0 [ V_{i*},V_{*i} ] ) \ge d/k$
;
$\delta ( G^0 [ V_{i*},V_{*i} ] ) \ge d/k$
; -
(ii)
 $\sum _{i',j' \in [k] \colon i' \ne j'} |V_{i'j'}| \le \gamma n$
;
$\sum _{i',j' \in [k] \colon i' \ne j'} |V_{i'j'}| \le \gamma n$
; -
(iii) for all
 $ v \in V_{ij}$
, we have
$ v \in V_{ij}$
, we have
 $ d^+(v,V_{*i}) - d^-(v, V_{i *}) \le \gamma n $
.
$ d^+(v,V_{*i}) - d^-(v, V_{i *}) \le \gamma n $
.
Then there exists a partition
![]() $\mathcal {P}' = \{V_{ii}':i \in [k]\}$
of
$\mathcal {P}' = \{V_{ii}':i \in [k]\}$
of
![]() $V(G^0)$
such that, for all
$V(G^0)$
such that, for all
![]() $i \in [k]$
,
$i \in [k]$
,
-
(i′)
 $|V_{ii} \triangle V^{\prime }_{ii}| \le \gamma n $
;
$|V_{ii} \triangle V^{\prime }_{ii}| \le \gamma n $
; -
(ii′)
 $\delta ^0( G^0 [ V_{ii}' ] ) \ge d/k - \gamma n $
.
$\delta ^0( G^0 [ V_{ii}' ] ) \ge d/k - \gamma n $
.
Proof. For each
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $V_{ii}' =V_{i*}$
. Clearly,
$V_{ii}' =V_{i*}$
. Clearly,
![]() $\mathcal {P}' = \{V_{ii}':i \in [k]\}$
is a partition of
$\mathcal {P}' = \{V_{ii}':i \in [k]\}$
is a partition of
![]() $V(G^0)$
. Note that (ii) implies (i
$V(G^0)$
. Note that (ii) implies (i
![]() $'$
). For
$'$
). For
![]() $v \in V_{ij}$
(possibly
$v \in V_{ij}$
(possibly
![]() $i=j$
), note that
$i=j$
), note that
If
![]() $i\neq j$
, similarly, we have
$i\neq j$
, similarly, we have
Also, for all
![]() $v\in V_{ii}$
, (i) implies
$v\in V_{ii}$
, (i) implies
![]() $d^{-}(v, V_{ii}')= d^{-}(v, V_{i*})\ge d/k$
. Hence (ii
$d^{-}(v, V_{ii}')= d^{-}(v, V_{i*})\ge d/k$
. Hence (ii
![]() $'$
) holds.
$'$
) holds.
Lemma 6.3. Let
![]() $d,k \in \mathbb {N}$
be such that
$d,k \in \mathbb {N}$
be such that
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $d> 165k^5$
. Let G be a d-regular digraph on n vertices and
$d> 165k^5$
. Let G be a d-regular digraph on n vertices and
![]() $\mathcal {P}=\{V_{ii}: i \in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ii}: i \in [k]\}$
be a partition of
![]() $V(G)$
such that, for all
$V(G)$
such that, for all
![]() $i \in [k]$
,
$i \in [k]$
,
-
(i)
 $|V_{ii}|\ge d/2$
;
$|V_{ii}|\ge d/2$
; -
(ii)
 $n<(2d+1)k$
, and
$n<(2d+1)k$
, and
 $n<(d+1)k$
if G is not oriented;
$n<(d+1)k$
if G is not oriented; -
(iii) for all
 $v \in V_{ii}$
,
$v \in V_{ii}$
,
 $d^+(v,V_{ii})+d^-(v,V_{ii})\ge d/k$
.
$d^+(v,V_{ii})+d^-(v,V_{ii})\ge d/k$
.
Then G contains a non-trivial
![]() $\mathcal {P}$
-balanced path system
$\mathcal {P}$
-balanced path system
![]() $\mathcal {Q}$
with
$\mathcal {Q}$
with
![]() $e (\mathcal {Q}) \le k$
.
$e (\mathcal {Q}) \le k$
.
Before we can prove Lemma 5.4, we need a good lower bound in oriented graphs for
![]() $|\bigcup _{i \in I} \left ( V_{i*} \cup V_{*i} \right )|$
for any connected component I in
$|\bigcup _{i \in I} \left ( V_{i*} \cup V_{*i} \right )|$
for any connected component I in
![]() $S(\mathcal {P})$
; see Proposition 6.5. For this, we use the following result on the minimum semi-degree threshold for an oriented graph to be a robust outexpander. Recall that the definition of robust outexpander is given immediately after Remark 3.3.
$S(\mathcal {P})$
; see Proposition 6.5. For this, we use the following result on the minimum semi-degree threshold for an oriented graph to be a robust outexpander. Recall that the definition of robust outexpander is given immediately after Remark 3.3.
Lemma 6.4 [Reference Kühn and Osthus22, Lemma 13.1]
Let
![]() $1/n \ll \nu \ll \tau \leq \varepsilon /2 \leq 1$
. Then every oriented graph G on n vertices with
$1/n \ll \nu \ll \tau \leq \varepsilon /2 \leq 1$
. Then every oriented graph G on n vertices with
![]() $\delta ^0(G)\ge (3/8+\varepsilon )n$
is a robust
$\delta ^0(G)\ge (3/8+\varepsilon )n$
is a robust
![]() $(\nu ,\tau )$
-outexpander.
$(\nu ,\tau )$
-outexpander.
Proposition 6.5. Let
![]() $1/ n \ll \gamma \ll \alpha , 1/k$
. Let G be an oriented graph on n vertices with
$1/ n \ll \gamma \ll \alpha , 1/k$
. Let G be an oriented graph on n vertices with
![]() $\Delta ^0(G)\le d$
where
$\Delta ^0(G)\le d$
where
![]() $ d \ge \alpha n$
. Let
$ d \ge \alpha n$
. Let
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G)$
such that
$V(G)$
such that
![]() $|V_{i*}| \ge d/2$
for all
$|V_{i*}| \ge d/2$
for all
![]() $i \in [k]$
. Suppose that, for all
$i \in [k]$
. Suppose that, for all
![]() $i,j \in [k]$
, all but at most
$i,j \in [k]$
, all but at most
![]() $\gamma n$
vertices
$\gamma n$
vertices
![]() $x\in V_{ij}$
satisfy
$x\in V_{ij}$
satisfy
![]() $d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
. Let
$d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
. Let
![]() $I \subseteq S(\mathcal {P})$
be a connected component. Then
$I \subseteq S(\mathcal {P})$
be a connected component. Then
 $$ \begin{align*} \left| \bigcup_{i \in I } (V_{i*} \cup V_{*i}) \right| \ge \begin{cases} 2(d - \gamma n) & \text{if }|I| =1,\\ 9(d - 5\gamma n)/4 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \left| \bigcup_{i \in I } (V_{i*} \cup V_{*i}) \right| \ge \begin{cases} 2(d - \gamma n) & \text{if }|I| =1,\\ 9(d - 5\gamma n)/4 & \text{otherwise.} \end{cases} \end{align*} $$
Proof. Without loss of generality, let
![]() $I = [\ell ]$
. For each
$I = [\ell ]$
. For each
![]() $i \in [\ell ]$
, we can find vertices
$i \in [\ell ]$
, we can find vertices
![]() $ v_i \in V_{i*}$
such that
$ v_i \in V_{i*}$
such that
![]() $d^+(v_i, V_{*i})\ge d - \gamma n $
as
$d^+(v_i, V_{*i})\ge d - \gamma n $
as
![]() $\gamma \ll \alpha ,1/k$
, which shows in particular that
$\gamma \ll \alpha ,1/k$
, which shows in particular that
![]() $|V_{*i}|\geq d-\gamma n$
. Hence, if
$|V_{*i}|\geq d-\gamma n$
. Hence, if
![]() $\ell \ge 3$
,
$\ell \ge 3$
,
 $$ \begin{align*} \left|\bigcup_{i \in I } (V_{i*} \cup V_{*i})\right| \ge \sum_{i \in [\ell] } | V_{*i}| \ge \ell (d - \gamma n) \ge 3(d-\gamma n)\ge 9(d-5\gamma n)/4. \end{align*} $$
$$ \begin{align*} \left|\bigcup_{i \in I } (V_{i*} \cup V_{*i})\right| \ge \sum_{i \in [\ell] } | V_{*i}| \ge \ell (d - \gamma n) \ge 3(d-\gamma n)\ge 9(d-5\gamma n)/4. \end{align*} $$
If
![]() $\ell = 1$
, then
$\ell = 1$
, then
![]() $V_{11} = V_{1*} = V_{*1}$
. There exists a vertex
$V_{11} = V_{1*} = V_{*1}$
. There exists a vertex
![]() $v \in V_{11}$
such that
$v \in V_{11}$
such that
![]() $d^+(v, V_{11}), d^-(v, V_{11}) \ge d - \gamma n $
. Since G is an oriented graph, we have
$d^+(v, V_{11}), d^-(v, V_{11}) \ge d - \gamma n $
. Since G is an oriented graph, we have
![]() $|V_{11}| \ge d^+(v, V_{11}) + d^-(v, V_{11}) \ge 2(d - \gamma n)$
.
$|V_{11}| \ge d^+(v, V_{11}) + d^-(v, V_{11}) \ge 2(d - \gamma n)$
.
If
![]() $\ell = 2$
, then
$\ell = 2$
, then
![]() $\bigcup _{i \in [2] } V_{i*} = \bigcup _{i \in [2] } V_{*i}$
and
$\bigcup _{i \in [2] } V_{i*} = \bigcup _{i \in [2] } V_{*i}$
and
![]() $V_{ij} = V_{ji} = \emptyset $
for all
$V_{ij} = V_{ji} = \emptyset $
for all
![]() $(i,j) \in [2] \times ([k] \setminus [2])$
. Let
$(i,j) \in [2] \times ([k] \setminus [2])$
. Let
![]() $V_I = \bigcup _{i \in [2] } V_{i*}=\bigcup _{i \in [2] } V_{*i}$
. There exists a vertex subset
$V_I = \bigcup _{i \in [2] } V_{i*}=\bigcup _{i \in [2] } V_{*i}$
. There exists a vertex subset
![]() $W \subseteq V_I$
such that
$W \subseteq V_I$
such that
and such that, writing
![]() $W_{ij} = W \cap V_{ij}$
for
$W_{ij} = W \cap V_{ij}$
for
![]() $i,j \in [2]$
, we have for all
$i,j \in [2]$
, we have for all
![]() $i,j \in [2]$
that
$i,j \in [2]$
that
Hence
![]() $\delta ^0( G[W] ) \ge d - 5\gamma n$
.
$\delta ^0( G[W] ) \ge d - 5\gamma n$
.
Let
![]() $\tau $
be a constant with
$\tau $
be a constant with
![]() $\gamma \ll \tau \ll \alpha $
. Next we show that
$\gamma \ll \tau \ll \alpha $
. Next we show that
![]() $G[W]$
is not a robust
$G[W]$
is not a robust
![]() $( \gamma ^{1/3} , \tau )$
-outexpander. For
$( \gamma ^{1/3} , \tau )$
-outexpander. For
![]() $i \in [2]$
, (6.1) implies that
$i \in [2]$
, (6.1) implies that
![]() $|W_{i*}| \geq d - 5 \gamma n \ge \tau n \ge \tau |W|$
and so
$|W_{i*}| \geq d - 5 \gamma n \ge \tau n \ge \tau |W|$
and so
![]() $\tau |W| \leq |W_{i*}| \leq (1 - \tau )|W|$
. Since
$\tau |W| \leq |W_{i*}| \leq (1 - \tau )|W|$
. Since
![]() $W_{1*} \cup W_{2*} = W_{*1} \cup W_{*2}$
, we may assume without loss of generality that
$W_{1*} \cup W_{2*} = W_{*1} \cup W_{*2}$
, we may assume without loss of generality that
![]() $|W_{1*}| \geq |W_{*1}|$
. Recall that
$|W_{1*}| \geq |W_{*1}|$
. Recall that
![]() $\Delta ^0(G) \le d$
. By (6.1), each vertex in
$\Delta ^0(G) \le d$
. By (6.1), each vertex in
![]() $|W_{1*}|$
has at most
$|W_{1*}|$
has at most
![]() $5\gamma n$
outneighbours in
$5\gamma n$
outneighbours in
![]() $W_{*2}$
, so
$W_{*2}$
, so
 $$ \begin{align*} |\mathrm{RN}_{\gamma^{1/3}}^+(W_{1*}) \cap W_{*2}| \leq \frac{e_G(W_{1*}, W_{*2})}{ \gamma^{1/3} |W|} \le \frac{5 \gamma n^2} {\alpha \gamma^{1/3} n } < \gamma^{1/3} \alpha n \le \gamma^{1/3} |W|, \end{align*} $$
$$ \begin{align*} |\mathrm{RN}_{\gamma^{1/3}}^+(W_{1*}) \cap W_{*2}| \leq \frac{e_G(W_{1*}, W_{*2})}{ \gamma^{1/3} |W|} \le \frac{5 \gamma n^2} {\alpha \gamma^{1/3} n } < \gamma^{1/3} \alpha n \le \gamma^{1/3} |W|, \end{align*} $$
where the penultimate inequality holds as
![]() $\gamma \ll \alpha $
. This implies that
$\gamma \ll \alpha $
. This implies that
Hence
![]() $G[W]$
is not a robust
$G[W]$
is not a robust
![]() $( \gamma ^{1/3}, \tau )$
-outexpander as claimed. Lemma 6.4 with
$( \gamma ^{1/3}, \tau )$
-outexpander as claimed. Lemma 6.4 with
![]() $\varepsilon =5/72$
implies
$\varepsilon =5/72$
implies
![]() $\delta ^0( G[W] ) \leq (3/8 + \varepsilon )|W| = 4|W|/9$
. Then
$\delta ^0( G[W] ) \leq (3/8 + \varepsilon )|W| = 4|W|/9$
. Then
![]() $4|W|/9 \geq d - 5\gamma n$
, and the result follows.
$4|W|/9 \geq d - 5\gamma n$
, and the result follows.
We now prove Lemma 5.4 assuming Lemmas 6.1 and 6.3.
Proof of Lemma 5.4
Let G and
![]() $\mathcal {P} = \{V_{ij}: i,j \in [k]\}$
be as in the statement of Lemma 5.4. We apply Lemma 6.1 (with
$\mathcal {P} = \{V_{ij}: i,j \in [k]\}$
be as in the statement of Lemma 5.4. We apply Lemma 6.1 (with
![]() $G^0 = G$
) and obtain a
$G^0 = G$
) and obtain a
![]() $\mathcal {P}$
-balanced path system
$\mathcal {P}$
-balanced path system
![]() $\mathcal {Q}^0$
such that
$\mathcal {Q}^0$
such that
![]() $e(\mathcal {Q}^0) \le k^2 \gamma n $
. Let
$e(\mathcal {Q}^0) \le k^2 \gamma n $
. Let
![]() $\mathcal {P}^{0}$
be the
$\mathcal {P}^{0}$
be the
![]() $\mathcal {Q}^0$
-contracted partition of
$\mathcal {Q}^0$
-contracted partition of
![]() $\mathcal {P}$
. Let
$\mathcal {P}$
. Let
![]() $k^*$
be the smallest integer larger than
$k^*$
be the smallest integer larger than
![]() $n/(qd+1)$
, that is,
$n/(qd+1)$
, that is,
![]() $k^* = \lfloor n/(qd+1) \rfloor +1 $
. If
$k^* = \lfloor n/(qd+1) \rfloor +1 $
. If
![]() $S(\mathcal {P}^{0})$
has at most
$S(\mathcal {P}^{0})$
has at most
![]() $n/(qd+1)$
connected components, then we are done by setting
$n/(qd+1)$
connected components, then we are done by setting
![]() $\mathcal {P}' = \mathcal {P}$
and
$\mathcal {P}' = \mathcal {P}$
and
![]() $\mathcal {Q}= \mathcal {Q}^0$
since
$\mathcal {Q}= \mathcal {Q}^0$
since
![]() $e(\mathcal {Q}^0) \le k^2 \gamma n\le \gamma ^{1/2} n $
. Hence we may assume that
$e(\mathcal {Q}^0) \le k^2 \gamma n\le \gamma ^{1/2} n $
. Hence we may assume that
![]() $S(\mathcal {P}^{0})$
has at least
$S(\mathcal {P}^{0})$
has at least
![]() $k^*$
connected components.
$k^*$
connected components.
Claim 6.6. We have
![]() $k^* = k$
and
$k^* = k$
and
![]() $S(\mathcal {P}^{0})$
is an empty graph on
$S(\mathcal {P}^{0})$
is an empty graph on
![]() $[k^*]$
.
$[k^*]$
.
Proof of claim
Since
![]() $1/n\ll \gamma \ll \alpha $
and
$1/n\ll \gamma \ll \alpha $
and
![]() $d \ge \alpha n$
, we have that
$d \ge \alpha n$
, we have that
 $$ \begin{align} \dfrac{n}{q(d-\gamma n)}-\dfrac{n}{qd+1}\leq \dfrac{1}{10}\text{ and so } \left\lfloor \frac{n}{ q (d-\gamma n ) } \right\rfloor \le \left\lfloor \frac{n}{q d+1} \right\rfloor +1 =k^*. \end{align} $$
$$ \begin{align} \dfrac{n}{q(d-\gamma n)}-\dfrac{n}{qd+1}\leq \dfrac{1}{10}\text{ and so } \left\lfloor \frac{n}{ q (d-\gamma n ) } \right\rfloor \le \left\lfloor \frac{n}{q d+1} \right\rfloor +1 =k^*. \end{align} $$
First suppose that G is not oriented, so
![]() $q=1$
. Recall (iii) that
$q=1$
. Recall (iii) that
![]() $|V_{i*}| \ge d - \gamma n $
for all
$|V_{i*}| \ge d - \gamma n $
for all
![]() $i \in [k]$
, so
$i \in [k]$
, so
![]() $n\geq k(d-\gamma n)$
. Together with (6.2), we have
$n\geq k(d-\gamma n)$
. Together with (6.2), we have
![]() $k \le \left \lfloor n/ (d-\gamma n) \right \rfloor \le k^*$
. On the other hand, since
$k \le \left \lfloor n/ (d-\gamma n) \right \rfloor \le k^*$
. On the other hand, since
![]() $S(\mathcal {P}^{0})$
has at least
$S(\mathcal {P}^{0})$
has at least
![]() $k^*$
connected components, we have
$k^*$
connected components, we have
![]() $k = | V( S(\mathcal {P}^{0}) ) | \ge k^*$
. Thus
$k = | V( S(\mathcal {P}^{0}) ) | \ge k^*$
. Thus
![]() $k = k^*$
. Furthermore,
$k = k^*$
. Furthermore,
![]() $S(\mathcal {P}^{0})$
is an empty graph on
$S(\mathcal {P}^{0})$
is an empty graph on
![]() $[k^*]$
(or else
$[k^*]$
(or else
![]() $S(\mathcal {P}^{0})$
would have fewer than
$S(\mathcal {P}^{0})$
would have fewer than
![]() $k^*$
connected components).
$k^*$
connected components).
Next, suppose that G is oriented, so
![]() $q=2$
. Let
$q=2$
. Let
![]() $I_1 , \dots , I_{a+b}$
be connected components of
$I_1 , \dots , I_{a+b}$
be connected components of
![]() $S(\mathcal {P}^{0})$
such that
$S(\mathcal {P}^{0})$
such that
![]() $|I_j| = 1$
if and only if
$|I_j| = 1$
if and only if
![]() $j \in [a]$
. Note that
$j \in [a]$
. Note that
![]() $ a+b \ge k^*$
and
$ a+b \ge k^*$
and
![]() $\{ \bigcup _{i \in I_j } (V_{i*} \cup V_{*i}) : j \in [a+b] \}$
is a partition of
$\{ \bigcup _{i \in I_j } (V_{i*} \cup V_{*i}) : j \in [a+b] \}$
is a partition of
![]() $V(G)$
. Recall (iv) that for all
$V(G)$
. Recall (iv) that for all
![]() $i,j\in [k]$
, all but at most
$i,j\in [k]$
, all but at most
![]() $\gamma n $
vertices
$\gamma n $
vertices
![]() $x \in V_{ij}$
satisfy
$x \in V_{ij}$
satisfy
![]() $d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
. Also, we have that
$d^+(x, V_{*i}), d^-(x, V_{j*}) \ge d - \gamma n $
. Also, we have that
![]() $|V_{i*}|\geq d-\gamma n\geq d/2$
for all
$|V_{i*}|\geq d-\gamma n\geq d/2$
for all
![]() $i\in [k]$
as
$i\in [k]$
as
![]() $\gamma \ll \alpha $
. By Proposition 6.5, we have
$\gamma \ll \alpha $
. By Proposition 6.5, we have
 $$ \begin{align*} n = \sum_{j \in [a+b]} \left| \bigcup_{i \in I_j } (V_{i*} \cup V_{*i}) \right| \ge 2(d-\gamma n) a + \frac{9(d-5\gamma n)}4 b =2(d-\gamma n)(a+b)+\dfrac{d-37\gamma n}{4}b. \end{align*} $$
$$ \begin{align*} n = \sum_{j \in [a+b]} \left| \bigcup_{i \in I_j } (V_{i*} \cup V_{*i}) \right| \ge 2(d-\gamma n) a + \frac{9(d-5\gamma n)}4 b =2(d-\gamma n)(a+b)+\dfrac{d-37\gamma n}{4}b. \end{align*} $$
Hence (6.2) implies that
where the last inequality holds as
![]() $\gamma \ll \alpha $
. Recalling that
$\gamma \ll \alpha $
. Recalling that
![]() $a+b \geq k^*$
, this shows that
$a+b \geq k^*$
, this shows that
![]() $a+b=k$
and
$a+b=k$
and
![]() $b = 0 $
, and so
$b = 0 $
, and so
![]() $ a = k^*$
, proving the claim.
$ a = k^*$
, proving the claim.
Since
![]() $S(\mathcal {P}^{0})$
is an empty graph on
$S(\mathcal {P}^{0})$
is an empty graph on
![]() $[k^*]$
, we deduce that
$[k^*]$
, we deduce that
![]() $\mathcal {Q}^0$
is trivial as defined at the start of the section. By the moreover statement of Lemma 6.1, we have
$\mathcal {Q}^0$
is trivial as defined at the start of the section. By the moreover statement of Lemma 6.1, we have
-
 $(\overline{\mathrm{m}1})\ \ \!\sum _{i,j \in [k] \colon i \ne j} |V_{ij}| \le k^2\gamma n \le \gamma ^{1/4} n$
and
$(\overline{\mathrm{m}1})\ \ \!\sum _{i,j \in [k] \colon i \ne j} |V_{ij}| \le k^2\gamma n \le \gamma ^{1/4} n$
and -
 $(\overline{\mathrm{m}2})$
for all distinct
$(\overline{\mathrm{m}2})$
for all distinct
 $i,j \in [k]$
and
$i,j \in [k]$
and
 $ v \in V_{ij}$
, we have
$ v \in V_{ij}$
, we have
 $ d^+(v,V_{*i}) - d^-(v, V_{i *}) \le 100k^{12} \gamma ^{1/3}d \le \gamma ^{1/4} n$
.
$ d^+(v,V_{*i}) - d^-(v, V_{i *}) \le 100k^{12} \gamma ^{1/3}d \le \gamma ^{1/4} n$
.
By Proposition 6.2 (with
![]() $\gamma ^{1/4}$
playing the role of
$\gamma ^{1/4}$
playing the role of
![]() $\gamma $
), there exists a partition
$\gamma $
), there exists a partition
![]() $\mathcal {P}' = \{V_{ii}':i \in [k]\}$
of
$\mathcal {P}' = \{V_{ii}':i \in [k]\}$
of
![]() $V(G)$
(and we take
$V(G)$
(and we take
![]() $V_{ij}' = \emptyset $
for
$V_{ij}' = \emptyset $
for
![]() $i \not = j$
) such that, for all
$i \not = j$
) such that, for all
![]() $i \in [k]$
,
$i \in [k]$
,
-
(i′)
 $|V_{ii} \triangle V^{\prime }_{ii}| \le \gamma ^{1/4} n $
;
$|V_{ii} \triangle V^{\prime }_{ii}| \le \gamma ^{1/4} n $
; -
(ii′)
 $\delta ^0( G [ V_{ii}' ] ) \ge (d/k) - \gamma ^{1/4} n $
.
$\delta ^0( G [ V_{ii}' ] ) \ge (d/k) - \gamma ^{1/4} n $
.
Finally, apply Lemma 6.3 (with
![]() $\mathcal {P}'$
playing the role of
$\mathcal {P}'$
playing the role of
![]() $\mathcal {P}$
) by noting that property (i) of Lemma 6.3 holds by property (iii) of Lemma 5.4 together with (
$\mathcal {P}$
) by noting that property (i) of Lemma 6.3 holds by property (iii) of Lemma 5.4 together with (
![]() $\overline {\text {m}1}$
) and (i
$\overline {\text {m}1}$
) and (i
![]() $'$
) above, and properties (ii) and (iii) of Lemma 6.3 hold by Claim 6.6 and (ii
$'$
) above, and properties (ii) and (iii) of Lemma 6.3 hold by Claim 6.6 and (ii
![]() $'$
) above, respectively. Thus, in G, we obtain a non-trivial
$'$
) above, respectively. Thus, in G, we obtain a non-trivial
![]() $\mathcal {P}'$
-balanced path system
$\mathcal {P}'$
-balanced path system
![]() $\mathcal {Q}$
with
$\mathcal {Q}$
with
![]() $ e (\mathcal {Q}) \le k \leq \gamma ^{1/2}n$
. Also, if
$ e (\mathcal {Q}) \le k \leq \gamma ^{1/2}n$
. Also, if
![]() $\mathcal {P}^*$
is the
$\mathcal {P}^*$
is the
![]() $\mathcal {Q}$
-contracted partition of
$\mathcal {Q}$
-contracted partition of
![]() $\mathcal {P}'$
, then by Claim 6.6,
$\mathcal {P}'$
, then by Claim 6.6,
![]() $S(\mathcal {P}^*)$
has at most
$S(\mathcal {P}^*)$
has at most
![]() $k-1=k^* - 1 \leq n/(qd + 1)$
connected components since
$k-1=k^* - 1 \leq n/(qd + 1)$
connected components since
![]() $\mathcal {Q}$
is non-trivial. This gives (c) and (d) in Lemma 5.4, while (
$\mathcal {Q}$
is non-trivial. This gives (c) and (d) in Lemma 5.4, while (
![]() $\overline {\text {m}1}$
) and (i
$\overline {\text {m}1}$
) and (i
![]() $'$
) imply (a), and (ii
$'$
) imply (a), and (ii
![]() $'$
) implies (b).
$'$
) implies (b).
7. Proof of Lemma 6.1
Recall that in Lemma 6.1, we are given a d-regular digraph
![]() $G^0$
on n vertices together with a partition
$G^0$
on n vertices together with a partition
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
of
![]() $V(G^0)$
satisfying certain size and degree conditions, and we must find a
$V(G^0)$
satisfying certain size and degree conditions, and we must find a
![]() $\mathcal {P}$
-balanced path system
$\mathcal {P}$
-balanced path system
![]() $\mathcal {Q}$
with few edges. Moreover, we require that
$\mathcal {Q}$
with few edges. Moreover, we require that
![]() $\mathcal {Q}$
is non-trivial under certain circumstances. We begin with a sketch of our proof approach for this lemma (ignoring the moreover part for now). Recall the definitions at the start of Sections 4 and 5.
$\mathcal {Q}$
is non-trivial under certain circumstances. We begin with a sketch of our proof approach for this lemma (ignoring the moreover part for now). Recall the definitions at the start of Sections 4 and 5.
Let
![]() $V^+$
and
$V^+$
and
![]() $V^-$
be two disjoint copies of
$V^-$
be two disjoint copies of
![]() $V(G^0)$
. Let
$V(G^0)$
. Let
![]() $V_{1*}^+, \dots , V_{k*}^+$
to be the partition of
$V_{1*}^+, \dots , V_{k*}^+$
to be the partition of
![]() $V^+$
corresponding to
$V^+$
corresponding to
![]() $V_{1*}, \dots , V_{k*}$
in
$V_{1*}, \dots , V_{k*}$
in
![]() $V(G^0)$
. Similarly, let
$V(G^0)$
. Similarly, let
![]() $V_{*1}^-, \dots , V_{*k}^-$
to be the partition of
$V_{*1}^-, \dots , V_{*k}^-$
to be the partition of
![]() $V^-$
corresponding to
$V^-$
corresponding to
![]() $V_{*1}, \dots , V_{*k}$
in
$V_{*1}, \dots , V_{*k}$
in
![]() $V(G^0)$
. Let H be the bipartite digraph with bipartition
$V(G^0)$
. Let H be the bipartite digraph with bipartition
![]() $V^+, V^-$
such that for each
$V^+, V^-$
such that for each
![]() $x \in V^+_{i*}$
and
$x \in V^+_{i*}$
and
![]() $y \in V^-_{*j}$
, we have
$y \in V^-_{*j}$
, we have
![]() $xy \in E(H)$
if and only if
$xy \in E(H)$
if and only if
![]() $xy \in E(G^0)$
and
$xy \in E(G^0)$
and
![]() $i \ne j$
. So there is a bijection between
$i \ne j$
. So there is a bijection between
![]() $E(H)$
and
$E(H)$
and
![]() $E(\mathcal {B}( G^0, \mathcal {P}))$
.
$E(\mathcal {B}( G^0, \mathcal {P}))$
.
A naive approach is to find, for each
![]() $i, j \in [k]$
with
$i, j \in [k]$
with
![]() $i \ne j$
, a matching
$i \ne j$
, a matching
![]() $M_{ij}$
in
$M_{ij}$
in
![]() $H[V_{i*}^+, V^-_{*j}]$
with
$H[V_{i*}^+, V^-_{*j}]$
with
![]() $e(M_{ij}) = e(G^0_{ij})/d$
. If
$e(M_{ij}) = e(G^0_{ij})/d$
. If
![]() $Q_{ij}$
is the subgraph in
$Q_{ij}$
is the subgraph in
![]() $G^0$
corresponding to
$G^0$
corresponding to
![]() $M_{ij}$
, then
$M_{ij}$
, then
![]() $Q = \bigcup _{i,j \in [k]} Q_{ij}$
is
$Q = \bigcup _{i,j \in [k]} Q_{ij}$
is
![]() $\mathcal {P}$
-balanced by construction since
$\mathcal {P}$
-balanced by construction since
![]() $G^0$
is d-regular. It is relatively easy to guarantee Q has few edges by first passing from
$G^0$
is d-regular. It is relatively easy to guarantee Q has few edges by first passing from
![]() $G^0$
to a suitable subdigraph G (see Proposition 7.6). However, there are three problems with this approach: (i)
$G^0$
to a suitable subdigraph G (see Proposition 7.6). However, there are three problems with this approach: (i)
![]() $\Delta ^0(Q)$
might be greater than one (meaning that Q is not a path system), (ii)
$\Delta ^0(Q)$
might be greater than one (meaning that Q is not a path system), (ii)
![]() $e(G^0_{ij})/d$
may not be an integer, and (iii) Q may contain cycles, even if
$e(G^0_{ij})/d$
may not be an integer, and (iii) Q may contain cycles, even if
![]() $\Delta ^0(Q) \leq 1$
.
$\Delta ^0(Q) \leq 1$
.
To overcome (i) and (ii), we consider a suitable flow problem by converting H to a network
![]() ${\mathcal {F}^* = (F^*,w, s^*, t^*)}$
as follows (the formal definition of a network and flow are stated in Section 7.1). Starting with the graph H (with all edges of H having capacity 1), we add new vertices
${\mathcal {F}^* = (F^*,w, s^*, t^*)}$
as follows (the formal definition of a network and flow are stated in Section 7.1). Starting with the graph H (with all edges of H having capacity 1), we add new vertices
![]() $s^*, s_1, \dots , s_k, t^*, t_1, \dots , t_k$
, where
$s^*, s_1, \dots , s_k, t^*, t_1, \dots , t_k$
, where
![]() $s^*$
and
$s^*$
and
![]() $t^*$
are the source and sink respectively and where the
$t^*$
are the source and sink respectively and where the
![]() $s_i$
and
$s_i$
and
![]() $t_j$
are viewed as ‘local’ sources and sinks, respectively. For each
$t_j$
are viewed as ‘local’ sources and sinks, respectively. For each
![]() $i,j \in [k]$
and each
$i,j \in [k]$
and each
![]() $x^+ \in V^+_{i*}$
,
$x^+ \in V^+_{i*}$
,
![]() $y^- \in V^-_{*j}$
, we add the edges
$y^- \in V^-_{*j}$
, we add the edges
![]() $s_i x^+$
and
$s_i x^+$
and
![]() $y^- t_j$
, each of capacity
$y^- t_j$
, each of capacity
![]() $1$
. For each
$1$
. For each
![]() $i \in [k]$
, we add the edge
$i \in [k]$
, we add the edge
![]() $s^* s_i$
of capacity
$s^* s_i$
of capacity
![]() $\max \{|V_{i*}| - |V_{*i}|, 0\}$
, the edge
$\max \{|V_{i*}| - |V_{*i}|, 0\}$
, the edge
![]() $t_i t^*$
of capacity
$t_i t^*$
of capacity
![]() $\max \{|V_{*i}| - |V_{i*}|, 0\}$
and the edge
$\max \{|V_{*i}| - |V_{i*}|, 0\}$
and the edge
![]() $t_i s_i$
of infinite capacity. This gives the network
$t_i s_i$
of infinite capacity. This gives the network
![]() $\mathcal {F}^*$
; see Figure 1. Consider a maximum integer flow f for
$\mathcal {F}^*$
; see Figure 1. Consider a maximum integer flow f for
![]() $\mathcal {F}^*$
. Define Q to be the subdigraph of
$\mathcal {F}^*$
. Define Q to be the subdigraph of
![]() $\mathcal {B}(G^0, \mathcal {P})$
such that
$\mathcal {B}(G^0, \mathcal {P})$
such that
![]() $xy \in E(Q)$
if and only if
$xy \in E(Q)$
if and only if
![]() $x^+ y^-$
has a flow of one in f, where
$x^+ y^-$
has a flow of one in f, where
![]() $x^+$
and
$x^+$
and
![]() $y^-$
are the corresponding copies of x and y in
$y^-$
are the corresponding copies of x and y in
![]() $V^+$
and
$V^+$
and
![]() $V^-$
, respectively. Note that
$V^-$
, respectively. Note that
![]() $\Delta ^0(Q) \le 1$
by construction. Also it is easy to check that Q is
$\Delta ^0(Q) \le 1$
by construction. Also it is easy to check that Q is
![]() $\mathcal {P}$
-balanced provided all edges at
$\mathcal {P}$
-balanced provided all edges at
![]() $s^*$
(and hence also at
$s^*$
(and hence also at
![]() $t^*$
) are saturated by f.
$t^*$
) are saturated by f.

Figure 1 The network
![]() $\mathcal {F}^*$
.
$\mathcal {F}^*$
.
To guarantee this latter condition on f, it turns out that it is enough to find a fractional flow
![]() $f^*$
such that
$f^*$
such that
![]() $f_{ij}^*$
, the total amount of flow in
$f_{ij}^*$
, the total amount of flow in
![]() $f^*$
through the edges in
$f^*$
through the edges in
![]() $H[V_{i*},V_{*j}]$
, is roughly
$H[V_{i*},V_{*j}]$
, is roughly
![]() $e(G^0_{ij})/d$
for all
$e(G^0_{ij})/d$
for all
![]() $i\neq j$
. Such a fractional flow is almost a maximum flow, and we can use the max-flow min-cut theorem to convert this fractional flow into an integer flow that saturates the edges at
$i\neq j$
. Such a fractional flow is almost a maximum flow, and we can use the max-flow min-cut theorem to convert this fractional flow into an integer flow that saturates the edges at
![]() $s^*$
(and
$s^*$
(and
![]() $t^*$
); see Claim 7.10. This also addresses (ii) above.
$t^*$
); see Claim 7.10. This also addresses (ii) above.
To deal with (iii), suppose we could find a matching
![]() $M^0$
of
$M^0$
of
![]() $G^0$
such that
$G^0$
such that
![]() $e(M^0[V_{i*},V_{*j}]) \ge e(G^0_{ij})/d$
for all
$e(M^0[V_{i*},V_{*j}]) \ge e(G^0_{ij})/d$
for all
![]() $i,j \in [k]$
. Then defining H (and
$i,j \in [k]$
. Then defining H (and
![]() $\mathcal {F}^*$
) using
$\mathcal {F}^*$
) using
![]() $M^0$
instead of
$M^0$
instead of
![]() $G^0$
, we could apply the same argument as before to obtain a
$G^0$
, we could apply the same argument as before to obtain a
![]() $\mathcal {P}$
-balanced subgraph
$\mathcal {P}$
-balanced subgraph
![]() $Q \subseteq M^0$
(which is therefore necessarily a path system as required). However, it is not always possible to find such a matching, so instead, for each
$Q \subseteq M^0$
(which is therefore necessarily a path system as required). However, it is not always possible to find such a matching, so instead, for each
![]() $i,j$
, we find a large ‘extendable matching’ in
$i,j$
, we find a large ‘extendable matching’ in
![]() $G^0_{ij}$
which consists of a matching
$G^0_{ij}$
which consists of a matching
![]() $M_{ij} \subseteq G^0_{ij}$
together with sets of vertices
$M_{ij} \subseteq G^0_{ij}$
together with sets of vertices
![]() $X_{ij}^+ \subseteq V_{i*}$
and
$X_{ij}^+ \subseteq V_{i*}$
and
![]() $X_{ij}^- \subseteq V_{*j}$
where each vertex
$X_{ij}^- \subseteq V_{*j}$
where each vertex
![]() $v^+ \in X_{ij}^+$
has high outdegree in
$v^+ \in X_{ij}^+$
has high outdegree in
![]() $G^0_{ij}$
and each vertex
$G^0_{ij}$
and each vertex
![]() $v^- \in X_{ij}^-$
has high indegree in
$v^- \in X_{ij}^-$
has high indegree in
![]() $G^0_{ij}$
, and where
$G^0_{ij}$
, and where
![]() $\bigcup _{i,j} M_{ij}$
is a matching (see Lemma 7.8). Here the very large degrees of vertices in
$\bigcup _{i,j} M_{ij}$
is a matching (see Lemma 7.8). Here the very large degrees of vertices in
![]() $X_{ij} = X_{ij}^+ \cup X_{ij}^-$
allow us to greedily extend
$X_{ij} = X_{ij}^+ \cup X_{ij}^-$
allow us to greedily extend
![]() $M_{ij}$
into a suitably large path systemFootnote 5 (see Proposition 7.9). These path systems would be disjoint (as required) if the
$M_{ij}$
into a suitably large path systemFootnote 5 (see Proposition 7.9). These path systems would be disjoint (as required) if the
![]() $X_{ij}$
are disjoint, but a priori the
$X_{ij}$
are disjoint, but a priori the
![]() $X_{ij}$
will not be disjoint. Therefore, we must modify the
$X_{ij}$
will not be disjoint. Therefore, we must modify the
![]() $X_{ij}$
so that each vertex is assigned to at most one
$X_{ij}$
so that each vertex is assigned to at most one
![]() $X_{ij}^+$
and at most one
$X_{ij}^+$
and at most one
![]() $X_{ij}^-$
. It turns out that this assignment problem is not too hard to incorporate into the flow problem described earlier (we simply add an edge of capacity
$X_{ij}^-$
. It turns out that this assignment problem is not too hard to incorporate into the flow problem described earlier (we simply add an edge of capacity
![]() $1$
from
$1$
from
![]() $v^+ \in V^+$
to
$v^+ \in V^+$
to
![]() $t_j$
if
$t_j$
if
![]() $v^+ \in X_{ij}^+$
and similarly if
$v^+ \in X_{ij}^+$
and similarly if
![]() $v^- \in X_{ij}^-$
). Solving the flow problem gives us the disjoint ‘extendable matchings’ we seek (meaning the
$v^- \in X_{ij}^-$
). Solving the flow problem gives us the disjoint ‘extendable matchings’ we seek (meaning the
![]() $X_{ij}$
’s are disjoint), which can greedily be extended to give the desired path system.
$X_{ij}$
’s are disjoint), which can greedily be extended to give the desired path system.
7.1. Flows
We recall some common definitions and facts about flow networks. We note that flows are only used in the proof of Lemma 6.1 (and not in any preliminary results).
A flow network is a tuple
![]() $\mathcal {F} = (F,w,S,T)$
, where F is a digraph,
$\mathcal {F} = (F,w,S,T)$
, where F is a digraph,
![]() $w\colon E(F) \to \mathbb {R}_{\geq 0}$
is the capacity function, and
$w\colon E(F) \to \mathbb {R}_{\geq 0}$
is the capacity function, and
![]() $S \subset V$
is a set of sources (i.e., each
$S \subset V$
is a set of sources (i.e., each
![]() $s \in S$
only has outedges incident to it) and
$s \in S$
only has outedges incident to it) and
![]() $T \subset V$
is a set of sinks (i.e., each
$T \subset V$
is a set of sinks (i.e., each
![]() $t \in T$
only has inedges incident to it). A flow for the flow network
$t \in T$
only has inedges incident to it). A flow for the flow network
![]() $\mathcal {F}$
is a function
$\mathcal {F}$
is a function
![]() $f \colon E(F) \to \mathbb {R}_{\geq 0}$
such that, for all
$f \colon E(F) \to \mathbb {R}_{\geq 0}$
such that, for all
![]() $e\in E$
, we have
$e\in E$
, we have
![]() $f(e)\leq w(e)$
and, for all
$f(e)\leq w(e)$
and, for all
![]() $v\in V\setminus (S \cup T)$
, we have
$v\in V\setminus (S \cup T)$
, we have
![]() $\sum _{u\in N^-_F(v)}f(uv)=\sum _{u\in N^+_F(v)}f(vu)$
. We define the value of f as
$\sum _{u\in N^-_F(v)}f(uv)=\sum _{u\in N^+_F(v)}f(vu)$
. We define the value of f as ![]() . A maximum flow in a given flow network is a flow f that maximises
. A maximum flow in a given flow network is a flow f that maximises
![]() $val(f)$
. We say that f is an integer flow if
$val(f)$
. We say that f is an integer flow if
![]() $f(e)$
is an integer for all
$f(e)$
is an integer for all
![]() $e \in E$
, and to emphasize the contrast, we sometimes refer to a flow that is not necessarily an integer flow as a fractional flow. For any set of edges
$e \in E$
, and to emphasize the contrast, we sometimes refer to a flow that is not necessarily an integer flow as a fractional flow. For any set of edges
![]() $E' \subseteq E$
, we write
$E' \subseteq E$
, we write
![]() $f(E'):= \sum _{e \in E'}f(e)$
. If
$f(E'):= \sum _{e \in E'}f(e)$
. If
![]() $S = \{s\}$
and
$S = \{s\}$
and
![]() $T = \{t\}$
, then we simply write
$T = \{t\}$
, then we simply write
![]() $(F,w,s,t)$
.
$(F,w,s,t)$
.
There are variants of the above notions that we will use. In particular, as well as having edge capacities, a flow network can also have vertex capacities (which restrict the amount of flow that can pass through a vertex) so that now
![]() $w: E(F) \cup V(F) \to \mathbb {R}^+$
, and for each
$w: E(F) \cup V(F) \to \mathbb {R}^+$
, and for each
![]() $v \in V(F) \setminus (S \cup T) $
a flow is defined as before with the added restriction that
$v \in V(F) \setminus (S \cup T) $
a flow is defined as before with the added restriction that
![]() $f(v) \leq w(v)$
, where
$f(v) \leq w(v)$
, where
![]() $f(v):=\sum _{u\in N^-_F(v)}f(uv)=\sum _{u\in N^+_F(v)}f(vu)$
. One can easily reduce this to the situation of just edge capacities by replacing each vertex v with a directed edge
$f(v):=\sum _{u\in N^-_F(v)}f(uv)=\sum _{u\in N^+_F(v)}f(vu)$
. One can easily reduce this to the situation of just edge capacities by replacing each vertex v with a directed edge
![]() $v^-v^+$
of capacity
$v^-v^+$
of capacity
![]() $w(v)$
and each directed edge
$w(v)$
and each directed edge
![]() $uv$
(or
$uv$
(or
![]() $vw$
) with
$vw$
) with
![]() $uv^-$
(or
$uv^-$
(or
![]() $v^+w$
, respectively) where new edges inherit the capacities of their old counterparts. We say that a flow f saturates an edge e (or a vertex v) if
$v^+w$
, respectively) where new edges inherit the capacities of their old counterparts. We say that a flow f saturates an edge e (or a vertex v) if
![]() $f(e) = w(e)$
(or
$f(e) = w(e)$
(or
![]() $f(v) = w(v)$
, respectively).
$f(v) = w(v)$
, respectively).
Let
![]() $(F,w,s,t)$
be a flow network. For a partition
$(F,w,s,t)$
be a flow network. For a partition
![]() $(U,W)$
of
$(U,W)$
of
![]() $V(F)$
with
$V(F)$
with
![]() $s\in U$
,
$s\in U$
,
![]() $t\in W$
the edge set
$t\in W$
the edge set
![]() $E_F(U,W)$
is called a cut. (Recall that
$E_F(U,W)$
is called a cut. (Recall that
![]() $E_F(U,W)$
is the set of edges in F from U to W.) The capacity of a cut
$E_F(U,W)$
is the set of edges in F from U to W.) The capacity of a cut
![]() $E_F(U,W)$
is the sum of the capacities of its edges, (i.e.,
$E_F(U,W)$
is the sum of the capacities of its edges, (i.e., ![]() .) A minimum cut of the given flow network is a cut of minimum capacity. We make use of the following well-known theorem.
.) A minimum cut of the given flow network is a cut of minimum capacity. We make use of the following well-known theorem.
Theorem 7.1 (Max-flow min-cut [Reference Dantzig and Fulkerson4])
Let
![]() $(F,w,s,t)$
be a flow network.
$(F,w,s,t)$
be a flow network.
-
(i) If f is a flow and
 $E_F(U,W)$
is a cut then
$E_F(U,W)$
is a cut then
 $val(f) \leq w(E_F(U,W))$
.
$val(f) \leq w(E_F(U,W))$
. -
(ii) We have that f is a maximum flow and
 $E_F(U,W)$
is a minimum cut if and only if
$E_F(U,W)$
is a minimum cut if and only if
 $val(f)=w(E_F(U,W))$
and in that case f saturates every edge in
$val(f)=w(E_F(U,W))$
and in that case f saturates every edge in
 $E_F(U,W)$
.
$E_F(U,W)$
. -
(iii) If all capacities are non-negative integers, [i.e.,
 $w(e) \in \mathbb {Z}_{\geq 0}$
for all
$w(e) \in \mathbb {Z}_{\geq 0}$
for all
 $e \in E(F)$
], then there exists a maximum flow f that is an integer flow.
$e \in E(F)$
], then there exists a maximum flow f that is an integer flow.
We also use the following whose proof is omitted as it is straightforward.
Proposition 7.2. Let
![]() $\mathcal {F} = (F,w,s,t)$
be a flow network and f a flow for
$\mathcal {F} = (F,w,s,t)$
be a flow network and f a flow for
![]() $\mathcal {F}$
. Then, for any edge
$\mathcal {F}$
. Then, for any edge
![]() $e\in E(F)$
, there exists a flow
$e\in E(F)$
, there exists a flow
![]() $f'$
for
$f'$
for
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $f'(e)=0$
and
$f'(e)=0$
and
![]() $val(f') \ge val(f)-f(e)$
.
$val(f') \ge val(f)-f(e)$
.
7.2. Preliminaries
We will require Vizing’s theorem for multigraphs in the proof of Lemma 7.8. Let H be an (undirected) multigraph (without loops). The multiplicity
![]() $\mu (H)$
of H is the maximum number of edges between two vertices of H, and, as usual,
$\mu (H)$
of H is the maximum number of edges between two vertices of H, and, as usual,
![]() $\Delta (H)$
is the maximum degree of H. A proper k-edge-colouring of H is an assignment of k colours to the edges of H such that incident edges receive different colours.
$\Delta (H)$
is the maximum degree of H. A proper k-edge-colouring of H is an assignment of k colours to the edges of H such that incident edges receive different colours.
Theorem 7.3 ([Reference Vizing34]; see e.g., [Reference Diestel5])
Any multigraph H has a proper k-edge colouring with
![]() $k = \Delta (H) + \mu (H)$
colours. In particular, by taking the largest colour class, there is a matching in H of size at least
$k = \Delta (H) + \mu (H)$
colours. In particular, by taking the largest colour class, there is a matching in H of size at least
![]() $e(H)/(\Delta (G)+\mu (G))$
.
$e(H)/(\Delta (G)+\mu (G))$
.
We will also require the following simple proposition about decomposing acyclic digraphs into paths.
Proposition 7.4 [Reference Lo, Patel, Skokan and Talbot26, Proposition 2.6]
Let G be an acyclic digraph. Then the edges of G can be partitioned into
![]() $\sum _{v \in V(G)}\left | d^+(v) - d^-(v) \right |/2$
directed paths.
$\sum _{v \in V(G)}\left | d^+(v) - d^-(v) \right |/2$
directed paths.
We will need the following property of regular digraphs; its proof is a simple exercise by considering
![]() $ \sum _{v \in V_{i*}} d^+(v)$
and
$ \sum _{v \in V_{i*}} d^+(v)$
and
![]() $ \sum _{v \in V_{*i}} d^-(v)$
.
$ \sum _{v \in V_{*i}} d^-(v)$
.
Proposition 7.5 [Reference Lo, Patel and Yıldız27, Proposition 3.2]
Let G be a d-regular digraph,
![]() $k\in \mathbb {N}$
, and
$k\in \mathbb {N}$
, and
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G)$
. Then, for all
$V(G)$
. Then, for all
![]() $i \in [k]$
, we have
$i \in [k]$
, we have
![]() $d(|V_{i*}|-|V_{*i}|)= e( G_{i*} ) - e(G_{*i})$
.
$d(|V_{i*}|-|V_{*i}|)= e( G_{i*} ) - e(G_{*i})$
.
The next proposition shows that we can consider a simpler subgraph G in
![]() $\mathcal {B}( G^0 , \mathcal {P} )$
.
$\mathcal {B}( G^0 , \mathcal {P} )$
.
Proposition 7.6. Let
![]() $G^0$
be a digraph,
$G^0$
be a digraph,
![]() $k,d \in \mathbb {N}$
and
$k,d \in \mathbb {N}$
and
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G^0)$
such that for all
$V(G^0)$
such that for all
![]() $i \in [k]$
,
$i \in [k]$
,
![]() $e( G^0_{i*} ) - e(G^0_{*i}) = d ( |V_{i*}|-|V_{*i}| )$
. Then, by reordering
$e( G^0_{i*} ) - e(G^0_{*i}) = d ( |V_{i*}|-|V_{*i}| )$
. Then, by reordering
![]() $[k]$
if necessary, there exists a subdigraph G of
$[k]$
if necessary, there exists a subdigraph G of
![]() $\mathcal {B}(G^0, \mathcal {P})$
such that
$\mathcal {B}(G^0, \mathcal {P})$
such that
 $$ \begin{align*} e(G) & \le d (k-1) \sum_{i \in [k]}\left| |V_{i*}|-|V_{*i}| \right|/2,\\ e( G_{i*} ) - e(G_{*i}) & = d(|V_{i*}|-|V_{*i}|) \text{ for all }i \in [k], \end{align*} $$
$$ \begin{align*} e(G) & \le d (k-1) \sum_{i \in [k]}\left| |V_{i*}|-|V_{*i}| \right|/2,\\ e( G_{i*} ) - e(G_{*i}) & = d(|V_{i*}|-|V_{*i}|) \text{ for all }i \in [k], \end{align*} $$
and for all
![]() $i,j \in [k]$
with
$i,j \in [k]$
with
![]() $i \le j$
,
$i \le j$
,
![]() $e(G_{ji}) = 0$
.
$e(G_{ji}) = 0$
.
Proof. Define an auxiliary multidigraph
![]() $H^0$
on
$H^0$
on
![]() $[k]$
(with loops) such that there are precisely
$[k]$
(with loops) such that there are precisely
![]() $e(G^0_{ij})$
many
$e(G^0_{ij})$
many
![]() $ij$
edges in
$ij$
edges in
![]() $H^0$
. There is a natural bijection between
$H^0$
. There is a natural bijection between
![]() $E(G^0)$
and
$E(G^0)$
and
![]() $E(H^0)$
. Let H be an acyclic subdigraph of
$E(H^0)$
. Let H be an acyclic subdigraph of
![]() $H^0$
obtained by successively removing all edges of a directed cycle where we treat loops also as cycles. Note that, for all
$H^0$
obtained by successively removing all edges of a directed cycle where we treat loops also as cycles. Note that, for all
![]() $i \in [k]$
,
$i \in [k]$
,
Since H is acyclic, by relabelling if necessary, we may assume that there are no edges
![]() $ji$
with
$ji$
with
![]() $i \le j$
. By Proposition 7.4,
$i \le j$
. By Proposition 7.4,
![]() $E(H)$
can be decomposed into
$E(H)$
can be decomposed into
![]() $\sum _{i \in [k]}\left | d^+_{H}(i) - d^-_{H}(i) \right |/2$
directed paths. Since each path can have length at most
$\sum _{i \in [k]}\left | d^+_{H}(i) - d^-_{H}(i) \right |/2$
directed paths. Since each path can have length at most
![]() $k-1$
(as H has k vertices), we have
$k-1$
(as H has k vertices), we have

The result follows by setting G to be the subdigraph of
![]() $G^0$
corresponding to H.
$G^0$
corresponding to H.
We need the following lemma from our previous work [Reference Lo, Patel and Yıldız27]. It states that given a set of matchings of low total maximum degree, one can select a relatively large number of the edges from each matching so that the union of selected edges is also a matching.
Lemma 7.7 [Reference Lo, Patel and Yıldız27, Lemma 4.2]
Let
![]() $k,\ell \in \mathbb {N}$
and
$k,\ell \in \mathbb {N}$
and
![]() $M_1,M_2,\ldots ,M_{\ell }$
be matchings with
$M_1,M_2,\ldots ,M_{\ell }$
be matchings with
![]() $\Delta \left (\bigcup _{i \in [\ell ]} M_i\right )\leq k$
. Suppose
$\Delta \left (\bigcup _{i \in [\ell ]} M_i\right )\leq k$
. Suppose
![]() $e(M_i)> 8k^6\ln \ell $
for all
$e(M_i)> 8k^6\ln \ell $
for all
![]() $i \in [\ell ]$
. Then, there exists a matching
$i \in [\ell ]$
. Then, there exists a matching
![]() $M \subseteq \bigcup _{i \in [\ell ]}M_i$
with
$M \subseteq \bigcup _{i \in [\ell ]}M_i$
with
![]() $|M\cap M_i|\geq e(M_i)/2k^2$
for all
$|M\cap M_i|\geq e(M_i)/2k^2$
for all
![]() $i \in [\ell ]$
.
$i \in [\ell ]$
.
Any graph (or digraph) either has a large matching or has all its edges incident to a small set of vertices (so these vertices have relatively large degree). The following lemma allows us to interpolate between these extremes and moreover does it simultaneously for all
![]() $G_{ij}$
. This corresponds to the ‘extendable matchings’ described in the sketch of proof.
$G_{ij}$
. This corresponds to the ‘extendable matchings’ described in the sketch of proof.
Lemma 7.8. Let G be a digraph,
![]() $k,d\in \mathbb {N}$
, and
$k,d\in \mathbb {N}$
, and
![]() $\mathcal {P} = \{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P} = \{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G)$
. Let
$V(G)$
. Let
![]() $\theta \in (0,1)$
with
$\theta \in (0,1)$
with
![]() $\theta d \ge 2$
. For all
$\theta d \ge 2$
. For all
![]() $i,j \in [k]$
and
$i,j \in [k]$
and
![]() $v \in V(G)$
, let
$v \in V(G)$
, let
![]() $X_{ij}^+ = \{v \in V(G) : d_{G_{ij}}^+(v) \ge \theta d \}$
and define
$X_{ij}^+ = \{v \in V(G) : d_{G_{ij}}^+(v) \ge \theta d \}$
and define
![]() $X_{ij}^-$
similarly. Then, for each
$X_{ij}^-$
similarly. Then, for each
![]() $i,j \in [k]$
, there exists a matching
$i,j \in [k]$
, there exists a matching
![]() $M_{ij}$
of
$M_{ij}$
of
![]() $G_{ij}$
such that
$G_{ij}$
such that
-
(1)
 $ e(G_{ij}) \le \sum _{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum _{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) + (6 k^2 \theta d) e( M_{ij} ) + 50 k^{10} \theta d $
;
$ e(G_{ij}) \le \sum _{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum _{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) + (6 k^2 \theta d) e( M_{ij} ) + 50 k^{10} \theta d $
; -
(2) for all
 $uv \in M_{ij}$
,
$uv \in M_{ij}$
,
 $u \notin X_{ij}^+$
and
$u \notin X_{ij}^+$
and
 $v \notin X_{ij}^-$
;
$v \notin X_{ij}^-$
; -
(3)
 $\bigcup _{i,j \in [k]} M_{ij}$
is a matching.
$\bigcup _{i,j \in [k]} M_{ij}$
is a matching.
Proof. Consider
![]() $i,j \in [k]$
. Let
$i,j \in [k]$
. Let
![]() $H_{ij}$
be the multigraph obtained from
$H_{ij}$
be the multigraph obtained from
![]() $G_{ij}$
by deleting all the edges
$G_{ij}$
by deleting all the edges
![]() $uv$
with
$uv$
with
![]() $u\in X_{ij}^+$
or
$u\in X_{ij}^+$
or
![]() $v \in X_{ij}^-$
, and by making all the edges undirected. Note that we have
$v \in X_{ij}^-$
, and by making all the edges undirected. Note that we have
![]() $\Delta (H_{ij}) + \mu (H_{ij}) \leq 2\theta d+2$
and
$\Delta (H_{ij}) + \mu (H_{ij}) \leq 2\theta d+2$
and
 $$ \begin{align} e(H_{ij}) \geq e(G_{ij}) - \left( \sum_{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum_{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) \right). \end{align} $$
$$ \begin{align} e(H_{ij}) \geq e(G_{ij}) - \left( \sum_{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum_{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) \right). \end{align} $$
Then, by Vizing’s theorem for multigraphs (Theorem 7.3), there exists a matching
![]() $M_{ij}^H$
in
$M_{ij}^H$
in
![]() $H_{ij}$
of size at least
$H_{ij}$
of size at least
![]() $e(H_{ij})/(2\theta d+2) \ge e(H_{ij})/3\theta d$
. Let
$e(H_{ij})/(2\theta d+2) \ge e(H_{ij})/3\theta d$
. Let
![]() $M_{ij}^0$
be the corresponding matching in
$M_{ij}^0$
be the corresponding matching in
![]() $G_{ij}$
. If
$G_{ij}$
. If
![]() $e(M_{ij}^0) \le 16 k^{10}$
, then we set
$e(M_{ij}^0) \le 16 k^{10}$
, then we set
![]() $M_{ij}^0$
to be empty. Thus, together with (7.2) we have
$M_{ij}^0$
to be empty. Thus, together with (7.2) we have
 $$ \begin{align*} e(G_{ij}) \le \left( \sum_{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum_{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) \right) + (3 \theta d) e( M_{ij}^0 ) + 50 k^{10} \theta d. \end{align*} $$
$$ \begin{align*} e(G_{ij}) \le \left( \sum_{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum_{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) \right) + (3 \theta d) e( M_{ij}^0 ) + 50 k^{10} \theta d. \end{align*} $$
Observe that
![]() $\Delta \left (\bigcup _{i,j \in [k]} M_{ij}^0\right )\leq k$
. Apply Lemma 7.7 for nonempty matchings
$\Delta \left (\bigcup _{i,j \in [k]} M_{ij}^0\right )\leq k$
. Apply Lemma 7.7 for nonempty matchings
![]() $M_{ij}^0$
(with
$M_{ij}^0$
(with
![]() $\ell \le k^2$
) to obtain
$\ell \le k^2$
) to obtain
![]() $M_{ij} \subseteq M_{ij}^0$
(set
$M_{ij} \subseteq M_{ij}^0$
(set
![]() $M_{ij}=\emptyset $
if
$M_{ij}=\emptyset $
if
![]() $M_{ij}^0=\emptyset $
) such that
$M_{ij}^0=\emptyset $
) such that
![]() $\bigcup _{i,j \in [k]}M_{ij}$
is a matching and, for all
$\bigcup _{i,j \in [k]}M_{ij}$
is a matching and, for all
![]() $i,j \in [k]$
,
$i,j \in [k]$
,
![]() $e(M_{ij}) \ge e(M_{ij}^0) / 2k^2$
. The result follows.
$e(M_{ij}) \ge e(M_{ij}^0) / 2k^2$
. The result follows.
Recall that for any directed matching M,
![]() $V^+(M)$
and
$V^+(M)$
and
![]() $V^-(M)$
are the sets of starting and ending vertices of the directed edges in M, respectively. Formally,
$V^-(M)$
are the sets of starting and ending vertices of the directed edges in M, respectively. Formally,
![]() $V^+(M) =\{v\in V(M): vw\in E(M) \text { for some }w\in V(M) \}$
and similarly for
$V^+(M) =\{v\in V(M): vw\in E(M) \text { for some }w\in V(M) \}$
and similarly for
![]() $V^-(M)$
.
$V^-(M)$
.
Proposition 7.9. Let G be a digraph,
![]() $k\in \mathbb {N}$
, and
$k\in \mathbb {N}$
, and
![]() $\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
$\mathcal {P}=\{V_{ij}:i,j\in [k]\}$
be a partition of
![]() $V(G)$
. Let
$V(G)$
. Let
![]() $W \subseteq V(G)$
. Suppose that, for each
$W \subseteq V(G)$
. Suppose that, for each
![]() $i,j \in [k]$
with
$i,j \in [k]$
with
![]() $i \ne j$
, there exist
$i \ne j$
, there exist
![]() $Y_{ij}^+ \subseteq V_{i*}$
,
$Y_{ij}^+ \subseteq V_{i*}$
,
![]() $Y_{ij}^- \subseteq V_{*j}$
and
$Y_{ij}^- \subseteq V_{*j}$
and
![]() $M_{ij} \subseteq G_{ij}$
such that
$M_{ij} \subseteq G_{ij}$
such that
-
(a)
 $M = \bigcup _{i, j \in [k]} M_{ij}$
is a matching;
$M = \bigcup _{i, j \in [k]} M_{ij}$
is a matching; -
(b) both of
 $\{Y_{ij}^+, V^+(M_{ij}) : i,j \in [k] \}$
and
$\{Y_{ij}^+, V^+(M_{ij}) : i,j \in [k] \}$
and
 $\{ Y_{ij}^-, V^-(M_{ij}) : i,j \in [k] \}$
are sets of disjoint sets;
$\{ Y_{ij}^-, V^-(M_{ij}) : i,j \in [k] \}$
are sets of disjoint sets; -
(c) for all
 $y^+ \in Y_{ij}^+$
and
$y^+ \in Y_{ij}^+$
and
 $y^- \in Y_{ij}^-$
,
$y^- \in Y_{ij}^-$
,
 $d_{G_{ij}}^+(y^+),d_{G_{ij}}^-(y^-) \ge 2\sum _{i,j \in [k]} ( |Y_{ij}^+| + |Y_{ij}^-| + e(M_{ij}) ) + |W|+1$
.
$d_{G_{ij}}^+(y^+),d_{G_{ij}}^-(y^-) \ge 2\sum _{i,j \in [k]} ( |Y_{ij}^+| + |Y_{ij}^-| + e(M_{ij}) ) + |W|+1$
.
Then
![]() $\mathcal {B}(G, \mathcal {P})$
contains a path system
$\mathcal {B}(G, \mathcal {P})$
contains a path system
![]() $\mathcal {Q}$
such that the following hold:
$\mathcal {Q}$
such that the following hold:
-
(i)
 $e(\mathcal {Q}_{ij}) = |Y_{ij}^+| + |Y_{ij}^-| + e(M_{ij})$
for all
$e(\mathcal {Q}_{ij}) = |Y_{ij}^+| + |Y_{ij}^-| + e(M_{ij})$
for all
 $i,j \in [k]$
, where
$i,j \in [k]$
, where
 $\mathcal {Q}_{ij}=\mathcal {Q}\cap E(G_{ij})$
;
$\mathcal {Q}_{ij}=\mathcal {Q}\cap E(G_{ij})$
; -
(ii)
 $V(\mathcal {Q})\cap W \subseteq \bigcup _{i,j \in [k]} (Y_{ij}^+ \cup Y_{ij}^- \cup V(M_{ij})) $
;
$V(\mathcal {Q})\cap W \subseteq \bigcup _{i,j \in [k]} (Y_{ij}^+ \cup Y_{ij}^- \cup V(M_{ij})) $
; -
(iii) if
 $y^+\in Y_{ij}^+\setminus V^-(M)$
, then there exists
$y^+\in Y_{ij}^+\setminus V^-(M)$
, then there exists
 $u\in V_{*j}\setminus W$
such that the single edge
$u\in V_{*j}\setminus W$
such that the single edge
 $y^+u$
is a path in
$y^+u$
is a path in
 $\mathcal {Q}$
, and a similar statement for
$\mathcal {Q}$
, and a similar statement for
 $y^-\in Y_{ij}^-\setminus V^+(M)$
holds.
$y^-\in Y_{ij}^-\setminus V^+(M)$
holds.
Proof. Start by setting
![]() $\mathcal {Q}=M$
and then for each
$\mathcal {Q}=M$
and then for each
![]() $y \in Y_{ij}^+$
(and
$y \in Y_{ij}^+$
(and
![]() $y \in Y_{ij}^-$
), greedily add an edge
$y \in Y_{ij}^-$
), greedily add an edge
![]() $yv$
(and
$yv$
(and
![]() $vy$
, respectively) in
$vy$
, respectively) in
![]() $G_{ij} \setminus W$
such that v avoids all current vertices in
$G_{ij} \setminus W$
such that v avoids all current vertices in
![]() $\mathcal {Q}$
and all vertices in
$\mathcal {Q}$
and all vertices in
![]() $\bigcup _{i,j}(Y_{ij}^+\cup Y_{ij}^-)$
, which is possible by (c). It is clear that we always maintain a path system, and that (i)–(iii) hold by construction.
$\bigcup _{i,j}(Y_{ij}^+\cup Y_{ij}^-)$
, which is possible by (c). It is clear that we always maintain a path system, and that (i)–(iii) hold by construction.
7.3. Proof of Lemma 6.1
We now prove Lemma 6.1.
Proof of Lemma 6.1
We split the proof into several steps.
Step 1: Defining
![]() $\boldsymbol {G}$
. By Proposition 7.5,
$\boldsymbol {G}$
. By Proposition 7.5,
![]() $e( G^0_{i*} ) - e(G^0_{*i}) = d(|V_{i*}|-|V_{*i}|)$
for all
$e( G^0_{i*} ) - e(G^0_{*i}) = d(|V_{i*}|-|V_{*i}|)$
for all
![]() $i \in [k]$
. Apply Proposition 7.6 and, without loss of generality, obtain a subdigraph G of
$i \in [k]$
. Apply Proposition 7.6 and, without loss of generality, obtain a subdigraph G of
![]() $\mathcal {B}(G^0, \mathcal {P})$
such that
$\mathcal {B}(G^0, \mathcal {P})$
such that

and, for all
![]() $i,j \in [k]$
with
$i,j \in [k]$
with
![]() $i \le j$
,
$i \le j$
,
![]() $e(G_{ji}) = 0$
.
$e(G_{ji}) = 0$
.
Step 2: Finding
![]() $\mathbf {X_{ij}^+}$
,
$\mathbf {X_{ij}^+}$
,
![]() $\mathbf {X_{ij}^-}$
and
$\mathbf {X_{ij}^-}$
and
![]() $\mathbf {M_{ij}}$
. For all
$\mathbf {M_{ij}}$
. For all
![]() $i,j \in [k]$
, let
$i,j \in [k]$
, let
Observe that
![]() $X_{ij}^+\subseteq V_{i*}$
and
$X_{ij}^+\subseteq V_{i*}$
and
![]() $X_{ij}^-\subseteq V_{*j}$
for all
$X_{ij}^-\subseteq V_{*j}$
for all
![]() $i,j\in [k]$
. Note that
$i,j\in [k]$
. Note that
![]() $\gamma ^{1/3} d \ge \gamma ^{1/3} \alpha n \ge 2$
as
$\gamma ^{1/3} d \ge \gamma ^{1/3} \alpha n \ge 2$
as
![]() $1/n\ll \gamma \ll \alpha $
. Apply Lemma 7.8 to G (with
$1/n\ll \gamma \ll \alpha $
. Apply Lemma 7.8 to G (with
![]() $\theta = \gamma ^{1/3} $
) and obtain a matching
$\theta = \gamma ^{1/3} $
) and obtain a matching
![]() $M_{ij}$
of
$M_{ij}$
of
![]() $G_{ij}$
for
$G_{ij}$
for
![]() $i,j \in [k]$
, such that
$i,j \in [k]$
, such that
-
(i′)
 $e(G_{ij}) \le \sum _{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum _{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) + (6 k^2 \gamma ^{1/3} d) e( M_{ij} ) + 50 k^{10}\gamma ^{1/3} d $
;
$e(G_{ij}) \le \sum _{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum _{x^- \in X_{ij}^-} d_{G_{ij}}^-(x^-) + (6 k^2 \gamma ^{1/3} d) e( M_{ij} ) + 50 k^{10}\gamma ^{1/3} d $
; -
(ii′) for all
 $uv \in M_{ij}$
,
$uv \in M_{ij}$
,
 $u \notin X_{ij}^+$
and
$u \notin X_{ij}^+$
and
 $v \notin X_{ij}^-$
;
$v \notin X_{ij}^-$
; -
(iii′)
 $\bigcup _{i,j \in [k]} M_{ij}$
is a matching.
$\bigcup _{i,j \in [k]} M_{ij}$
is a matching.
By deleting vertices in
![]() $X_{ij}^+ \cup X_{ij}^-$
and edges of
$X_{ij}^+ \cup X_{ij}^-$
and edges of
![]() $M_{ij}$
if necessary, we may assume that the RHS of (i
$M_{ij}$
if necessary, we may assume that the RHS of (i
![]() $'$
) is bounded above by
$'$
) is bounded above by
![]() $e(G_{ij})+d$
. Hence
$e(G_{ij})+d$
. Hence
 $$ \begin{align*} \gamma^{1/3} d ( |X_{ij}^+|+ |X_{ij}^-|+ e( M_{ij} ) ) & \le \sum_{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum_{x^- \in X_{ij}^-} d_{G_{ij}}^- ( x^- ) + (6 k^2 \gamma^{1/3} d ) e( M_{ij} ) + 50 k^{10}\gamma^{1/3} d \\ & \le e(G_{ij})+ d \overset{{({{7.3}})}}{\le} k^2 \gamma d n +d \le \gamma^{2/3} k^{-2} d^2 /3, \end{align*} $$
$$ \begin{align*} \gamma^{1/3} d ( |X_{ij}^+|+ |X_{ij}^-|+ e( M_{ij} ) ) & \le \sum_{x^+ \in X_{ij}^+} d_{G_{ij}}^+(x^+) + \sum_{x^- \in X_{ij}^-} d_{G_{ij}}^- ( x^- ) + (6 k^2 \gamma^{1/3} d ) e( M_{ij} ) + 50 k^{10}\gamma^{1/3} d \\ & \le e(G_{ij})+ d \overset{{({{7.3}})}}{\le} k^2 \gamma d n +d \le \gamma^{2/3} k^{-2} d^2 /3, \end{align*} $$
where the last inequality holds as
![]() $d \ge \alpha n$
and
$d \ge \alpha n$
and
![]() $1/n \ll \gamma \ll \alpha , 1/k$
. Therefore,
$1/n \ll \gamma \ll \alpha , 1/k$
. Therefore,
-
(iv′)
 $\sum _{i,j \in [k]} \left ( |X_{ij}^+| + |X_{ij}^-| + e(M_{ij}) \right ) \le \gamma ^{1/3} d / 3 $
.
$\sum _{i,j \in [k]} \left ( |X_{ij}^+| + |X_{ij}^-| + e(M_{ij}) \right ) \le \gamma ^{1/3} d / 3 $
.
Step 3: Defining flow networks. For
![]() $i,j \in [k]$
, let
$i,j \in [k]$
, let
 $$ \begin{align*} M =\bigcup_{i,j \in [k]} M_{ij}, \quad X^+_{i*} = \bigcup_{j \in [k]} \left( X_{ij}^+ \cup V^+(M_{ij}) \right), \text{ and } X^-_{*j} = \bigcup_{i \in [k]} \left( X_{ij}^- \cup V^-(M_{ij}) \right). \end{align*} $$
$$ \begin{align*} M =\bigcup_{i,j \in [k]} M_{ij}, \quad X^+_{i*} = \bigcup_{j \in [k]} \left( X_{ij}^+ \cup V^+(M_{ij}) \right), \text{ and } X^-_{*j} = \bigcup_{i \in [k]} \left( X_{ij}^- \cup V^-(M_{ij}) \right). \end{align*} $$
Note that
![]() $X^+_{i*} \subseteq V_{i*}$
and
$X^+_{i*} \subseteq V_{i*}$
and
![]() $X^-_{*j} \subseteq V_{*j}$
. Let
$X^-_{*j} \subseteq V_{*j}$
. Let
![]() $X^+ = \bigcup _{i \in [k]} X^+_{i*}$
and
$X^+ = \bigcup _{i \in [k]} X^+_{i*}$
and
![]() $X^- = \bigcup _{j \in [k]} X^-_{*j}$
.
$X^- = \bigcup _{j \in [k]} X^-_{*j}$
.
We now define a flow network
![]() $\mathcal {F} = (F,w,S,T)$
with multiple sources and sinks as follows. Let
$\mathcal {F} = (F,w,S,T)$
with multiple sources and sinks as follows. Let
![]() $S= \{s_i: i \in [k]\}$
and
$S= \{s_i: i \in [k]\}$
and
![]() $T= \{t_i: i \in [k]\}$
. Let
$T= \{t_i: i \in [k]\}$
. Let
![]() $V(F) = S \cup T \cup X^+ \cup X^-$
. Here we treat
$V(F) = S \cup T \cup X^+ \cup X^-$
. Here we treat
![]() $X^+$
and
$X^+$
and
![]() $X^-$
as disjoint (i.e., both
$X^-$
as disjoint (i.e., both
![]() $X^+$
and
$X^+$
and
![]() $X^-$
contain a distinct copy of v for any vertex
$X^-$
contain a distinct copy of v for any vertex
![]() $v\in X^+\cap X^-$
). For
$v\in X^+\cap X^-$
). For
![]() $v \in V(G)$
, we write
$v \in V(G)$
, we write
![]() $v^+$
(and
$v^+$
(and
![]() $v^-$
) for the copy of v belonging to
$v^-$
) for the copy of v belonging to
![]() $X^+$
(and
$X^+$
(and
![]() $X^-$
, respectively). We define
$X^-$
, respectively). We define
![]() $E(F)$
as the union of edge-disjoint paths as follows: for each
$E(F)$
as the union of edge-disjoint paths as follows: for each
![]() $i,j \in [k]$
with
$i,j \in [k]$
with
![]() $i < j$
,
$i < j$
,
-
• for each
 $x^+ \in X_{ij}^+$
, we add the directed path
$x^+ \in X_{ij}^+$
, we add the directed path
 $s_{i} x^+ t_{j}$
;
$s_{i} x^+ t_{j}$
; -
• for each
 $x^- \in X_{ij}^-$
, we add the directed path
$x^- \in X_{ij}^-$
, we add the directed path
 $s_{i} x^- t_{j}$
;
$s_{i} x^- t_{j}$
; -
• for each
 $e = uv \in M_{ij}$
, we add the directed path
$e = uv \in M_{ij}$
, we add the directed path
 $s_{i} u^+ v^- t_{j}$
;
$s_{i} u^+ v^- t_{j}$
; -
• every edge and vertex has capacity
 $1$
(i.e.,
$1$
(i.e.,
 $w(e) = 1$
for all
$w(e) = 1$
for all
 $e \in E(F)$
and
$e \in E(F)$
and
 $w(v) = 1$
for all
$w(v) = 1$
for all
 $v \in V(F) \setminus (S \cup T) = X^+ \cup X^-$
).
$v \in V(F) \setminus (S \cup T) = X^+ \cup X^-$
).
We modify the flow network slightly if (m1) or (m2) holds. Let
 $$ \begin{align*} F_0=\begin{cases} F - \{v_0^+ \} - \{s_{i_0} v_0^-\} - E_F(X^+,v_0^-)&\text{ if }v_0\in V_{i_0j_0}\text{ exists satisfying (m2)},\\ F&\text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} F_0=\begin{cases} F - \{v_0^+ \} - \{s_{i_0} v_0^-\} - E_F(X^+,v_0^-)&\text{ if }v_0\in V_{i_0j_0}\text{ exists satisfying (m2)},\\ F&\text{ otherwise.} \end{cases} \end{align*} $$
We further remove
![]() $v_0^-$
from
$v_0^-$
from
![]() $F_0$
if
$F_0$
if
![]() $v_0^-$
has no inneighbour in
$v_0^-$
has no inneighbour in
![]() $F_0$
. Write
$F_0$
. Write
![]() $w_0$
for the capacities on
$w_0$
for the capacities on
![]() $F_0$
inherited from F and define
$F_0$
inherited from F and define
![]() $\mathcal {F}_0 = (F_0,w_0,S,T)$
. By the definition of
$\mathcal {F}_0 = (F_0,w_0,S,T)$
. By the definition of
![]() $\mathcal {F}_0$
, note for later that
$\mathcal {F}_0$
, note for later that
Given a flow f on
![]() $\mathcal {F}$
or
$\mathcal {F}$
or
![]() $\mathcal {F}_0$
, for each
$\mathcal {F}_0$
, for each
![]() $i,j \in [k]$
, let
$i,j \in [k]$
, let
![]() $f_{ij}$
be the sum of flow over all edges from
$f_{ij}$
be the sum of flow over all edges from
![]() $s_i \cup X^+_{i*}$
to
$s_i \cup X^+_{i*}$
to
![]() $ t_j \cup X^-_{*j}$
, that is,
$ t_j \cup X^-_{*j}$
, that is,
 $$ \begin{align} f_{ij} = \sum_{e \in E_F(s_i \cup X^+_{i*}, t_j \cup X^-_{*j})} f(e). \end{align} $$
$$ \begin{align} f_{ij} = \sum_{e \in E_F(s_i \cup X^+_{i*}, t_j \cup X^-_{*j})} f(e). \end{align} $$
Note that the total amount of flow going out of
![]() $s_i$
(all going to
$s_i$
(all going to
![]() $X^+$
) is
$X^+$
) is
![]() $\sum _{j\in [k]}f_{ij}$
, and the total amount of flow into
$\sum _{j\in [k]}f_{ij}$
, and the total amount of flow into
![]() $t_j$
is
$t_j$
is
![]() $\sum _{i\in [k]}f_{ij}$
. We now reduce the lemma to the following claim about fractional flows.
$\sum _{i\in [k]}f_{ij}$
. We now reduce the lemma to the following claim about fractional flows.
Claim 7.10. To prove the lemma, it suffices to find a fractional flow f on
![]() $\mathcal {F}_0$
such that
$\mathcal {F}_0$
such that
 $$ \begin{align} \sum_{i,j \in [k]} \max\{ e(G_{ij})/d - f_{ij}, 0 \} < 1. \end{align} $$
$$ \begin{align} \sum_{i,j \in [k]} \max\{ e(G_{ij})/d - f_{ij}, 0 \} < 1. \end{align} $$
Proof of claim
Assume f is as given in the claim and we wish to prove the lemma. We may assume that
![]() $f_{ij} \le e(G_{ij})/d$
for all
$f_{ij} \le e(G_{ij})/d$
for all
![]() $i,j \in [k]$
.Footnote 6 We define a new flow network
$i,j \in [k]$
.Footnote 6 We define a new flow network
![]() $\mathcal {F}^* = (F^*, w^*, s^*,t^*)$
with a single source
$\mathcal {F}^* = (F^*, w^*, s^*,t^*)$
with a single source
![]() $s^*$
and sink
$s^*$
and sink
![]() $t^*$
as follows. We obtain
$t^*$
as follows. We obtain
![]() $\mathcal {F}^*$
from
$\mathcal {F}^*$
from
![]() $\mathcal {F}_0$
by adding the new vertices
$\mathcal {F}_0$
by adding the new vertices
![]() $s^*$
and
$s^*$
and
![]() $t^*$
to
$t^*$
to
![]() $V(F_0)$
and, for each
$V(F_0)$
and, for each
![]() $i \in [k]$
,
$i \in [k]$
,
-
• adding the edge
 $s^* s_i$
of capacity
$s^* s_i$
of capacity
 $\max \{|V_{i*}| - |V_{*i}|, 0\}$
;
$\max \{|V_{i*}| - |V_{*i}|, 0\}$
; -
• adding the edge
 $t_i t^*$
of capacity
$t_i t^*$
of capacity
 $\max \{|V_{*i}| - |V_{i*}|, 0\}$
;
$\max \{|V_{*i}| - |V_{i*}|, 0\}$
; -
• adding an edge
 $t_i s_i$
of infinite capacity;
$t_i s_i$
of infinite capacity; -
• giving the vertices in
 $S \cup T$
infinite capacity.
$S \cup T$
infinite capacity.
We will use f to find an integer flow in
![]() $\mathcal {F}^*$
of value
$\mathcal {F}^*$
of value
![]() $ \sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
. Then, by looking at the vertices through which there is non-zero flow, we will define the sets
$ \sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
. Then, by looking at the vertices through which there is non-zero flow, we will define the sets
![]() $Y_{ij}^+$
,
$Y_{ij}^+$
,
![]() $Y_{ij}^+$
, and
$Y_{ij}^+$
, and
![]() $M_{ij}^*$
satisfying the properties for Proposition 7.9, which will give the desired path system
$M_{ij}^*$
satisfying the properties for Proposition 7.9, which will give the desired path system
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
First we find a fractional flow on
![]() $\mathcal {F}^*$
as follows. Let
$\mathcal {F}^*$
as follows. Let
![]() $\mathcal {F}^+ = (F^+, w^+,s^*,t^*)$
be obtained from
$\mathcal {F}^+ = (F^+, w^+,s^*,t^*)$
be obtained from
![]() $\mathcal {F}^*$
by adding, for each
$\mathcal {F}^*$
by adding, for each
![]() $i,j \in [k]$
, an edge
$i,j \in [k]$
, an edge
![]() $s_i t_j$
with edge capacity
$s_i t_j$
with edge capacity
![]() $1$
. Define a flow
$1$
. Define a flow
![]() $f^+$
on
$f^+$
on
![]() $\mathcal {F}^+$
such that, for all
$\mathcal {F}^+$
such that, for all
![]() $i,j \in [k]$
,
$i,j \in [k]$
,
-
•
 $f^+(e) = f(e)$
for all
$f^+(e) = f(e)$
for all
 $e \in E(F_0)$
;
$e \in E(F_0)$
; -
•
 $f^+(s^* s_i) = \max \{|V_{i*}| - |V_{*i}|, 0\} $
;
$f^+(s^* s_i) = \max \{|V_{i*}| - |V_{*i}|, 0\} $
; -
•
 $f^+(t_j t^*) = \max \{|V_{*j}| - |V_{j*}|, 0\}$
;
$f^+(t_j t^*) = \max \{|V_{*j}| - |V_{j*}|, 0\}$
; -
•
 $f^+(t_i s_i) = \min \{ e(G_{i*})/d, e(G_{*i})/d\}$
;
$f^+(t_i s_i) = \min \{ e(G_{i*})/d, e(G_{*i})/d\}$
; -
•
 $f^+(s_i t_j) = e(G_{ij})/d - f_{ij}\ge 0$
.
$f^+(s_i t_j) = e(G_{ij})/d - f_{ij}\ge 0$
.
One can check that
![]() $f^+$
is indeed a fractional flowFootnote 7 on
$f^+$
is indeed a fractional flowFootnote 7 on
![]() $\mathcal {F}^+$
with value
$\mathcal {F}^+$
with value
![]() $\sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
. By applying Proposition 7.2 to reduce the flow in
$\sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
. By applying Proposition 7.2 to reduce the flow in
![]() $s_it_j$
to
$s_it_j$
to
![]() $0$
for all
$0$
for all
![]() $i,j\in [k]$
, we obtain a fractional flow on
$i,j\in [k]$
, we obtain a fractional flow on
![]() $\mathcal {F}^*$
of value
$\mathcal {F}^*$
of value
 $$ \begin{align*} r & \geq \frac12\sum_{i \in [k]} \left| |V_{i*}| - |V_{*i}|\right| - \sum_{i,j \in [k]} f^+(s_it_j) = \frac12 \sum_{i \in [k]} \left| |V_{i*}| - |V_{*i}|\right| - \sum_{i,j \in [k]} \left( \frac{e(G_{ij})}d - f_{ij} \right)\\ & \overset{{({{7.8}})}}{>} \frac12\left(\sum_{i \in [k]} \left| |V_{i*}| - |V_{*i}|\right|\right)-1. \end{align*} $$
$$ \begin{align*} r & \geq \frac12\sum_{i \in [k]} \left| |V_{i*}| - |V_{*i}|\right| - \sum_{i,j \in [k]} f^+(s_it_j) = \frac12 \sum_{i \in [k]} \left| |V_{i*}| - |V_{*i}|\right| - \sum_{i,j \in [k]} \left( \frac{e(G_{ij})}d - f_{ij} \right)\\ & \overset{{({{7.8}})}}{>} \frac12\left(\sum_{i \in [k]} \left| |V_{i*}| - |V_{*i}|\right|\right)-1. \end{align*} $$
Note that all edge capacities are integral, so Theorem 7.1 implies there exists an integral flow
![]() $f^*$
on
$f^*$
on
![]() $\mathcal {F}^*$
of value at least
$\mathcal {F}^*$
of value at least
![]() $\lceil r \rceil = \sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
. Moreover, since the cuts
$\lceil r \rceil = \sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
. Moreover, since the cuts
![]() $E_{F^*}(s^*, V(F^*) \setminus \{s^*\})$
and
$E_{F^*}(s^*, V(F^*) \setminus \{s^*\})$
and
![]() $E_{F^*}( V(F^*) \setminus \{ t^*\}, t^*)$
have capacity
$E_{F^*}( V(F^*) \setminus \{ t^*\}, t^*)$
have capacity
![]() $\sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
, Theorem 7.1 implies that
$\sum _{i \in [k]} \left | |V_{i*}| - |V_{*i}|\right |/2$
, Theorem 7.1 implies that
![]() $f^*$
saturates all the edges
$f^*$
saturates all the edges
![]() $s^*s_i$
and
$s^*s_i$
and
![]() $t_jt^*$
for all
$t_jt^*$
for all
![]() $i,j \in [k]$
.
$i,j \in [k]$
.
We now define
![]() $Y_{ij}^+ \subseteq X_{ij}^+$
,
$Y_{ij}^+ \subseteq X_{ij}^+$
,
![]() $Y_{ij}^-\subseteq X_{ij}^-$
and
$Y_{ij}^-\subseteq X_{ij}^-$
and
![]() $M^*_{ij} \subseteq M_{ij}$
as follows. Initially, set
$M^*_{ij} \subseteq M_{ij}$
as follows. Initially, set
![]() $Y_{ij}^+ = Y_{ij}^- = M_{ij}= \emptyset $
for all
$Y_{ij}^+ = Y_{ij}^- = M_{ij}= \emptyset $
for all
![]() $i,j \in [k]$
. For each
$i,j \in [k]$
. For each
![]() $x^+\in X^+$
with
$x^+\in X^+$
with
![]() $f^*(x^+) = 1$
, since
$f^*(x^+) = 1$
, since
![]() $f^*$
is an integral flow, there exist unique
$f^*$
is an integral flow, there exist unique
![]() $i,j\in [k]$
such that either
$i,j\in [k]$
such that either
![]() $f^*(s_i x^+)=f^*(x^+t_j)=1$
or
$f^*(s_i x^+)=f^*(x^+t_j)=1$
or
![]() $f^*(s_i x^+)=f^*(x^+z)=f^*(zt_j)=1$
for some (unique)
$f^*(s_i x^+)=f^*(x^+z)=f^*(zt_j)=1$
for some (unique)
![]() $z\in X^-$
. In the former case we add
$z\in X^-$
. In the former case we add
![]() $x^+$
to
$x^+$
to
![]() $Y_{ij}^+$
while we add
$Y_{ij}^+$
while we add
![]() $x^+z$
into
$x^+z$
into
![]() $M_{ij}^*$
for the latter. In a similar way, for
$M_{ij}^*$
for the latter. In a similar way, for
![]() $x^- \in X^-$
with
$x^- \in X^-$
with
![]() $f^*(x^-) = 1$
, we either add
$f^*(x^-) = 1$
, we either add
![]() $x^-$
to the set
$x^-$
to the set
![]() $Y_{ij}^-$
or add an edge ending at
$Y_{ij}^-$
or add an edge ending at
![]() $x^-$
into
$x^-$
into
![]() $M_{ij}^*$
. Note that
$M_{ij}^*$
. Note that

Clearly
![]() $ M^* : = \bigcup _{i,j \in [k]} M^*_{ij} \subseteq M$
is a matching by (iii
$ M^* : = \bigcup _{i,j \in [k]} M^*_{ij} \subseteq M$
is a matching by (iii
![]() $'$
). Both of
$'$
). Both of
![]() $\{Y_{ij}^+, V^+(M_{ij}^*) : i,j \in [k] \}$
and
$\{Y_{ij}^+, V^+(M_{ij}^*) : i,j \in [k] \}$
and
![]() $\{ Y_{ij}^-, V^-(M_{ij}^*) : i,j \in [k] \}$
are sets of disjoint sets as each
$\{ Y_{ij}^-, V^-(M_{ij}^*) : i,j \in [k] \}$
are sets of disjoint sets as each
![]() $x \in X^+ \cup X^-$
has vertex capacity of one. Set
$x \in X^+ \cup X^-$
has vertex capacity of one. Set
 $$ \begin{align*} W = \begin{cases} \bigcup_{i,j \in [k] \colon i \ne j} V_{ij} & \text{if }\sum_{i,j \in [k] \colon i \ne j} |V_{ij}| \le k^2 \gamma n,\\ \emptyset & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} W = \begin{cases} \bigcup_{i,j \in [k] \colon i \ne j} V_{ij} & \text{if }\sum_{i,j \in [k] \colon i \ne j} |V_{ij}| \le k^2 \gamma n,\\ \emptyset & \text{otherwise.} \end{cases} \end{align*} $$
For all
![]() $y^+ \in Y_{ij}^+ \subseteq X_{ij}^+$
, we have
$y^+ \in Y_{ij}^+ \subseteq X_{ij}^+$
, we have

since
![]() $k^2\gamma n+1\le 2k^2\gamma n\le \gamma ^{1/3}d/3$
as
$k^2\gamma n+1\le 2k^2\gamma n\le \gamma ^{1/3}d/3$
as
![]() $\gamma \ll \alpha \le d/n$
, and a similar inequality holds for all
$\gamma \ll \alpha \le d/n$
, and a similar inequality holds for all
![]() $y^- \in Y_{ij}^-$
. We apply Proposition 7.9 and obtain a path system
$y^- \in Y_{ij}^-$
. We apply Proposition 7.9 and obtain a path system
![]() $\mathcal {Q}$
of G such that
$\mathcal {Q}$
of G such that
-
(i′′)
 for all
for all
 $i,j \in [k]$
;
$i,j \in [k]$
; -
(ii′′)
 $V(\mathcal {Q})\cap W \subseteq \bigcup _{i,j \in [k]} (Y_{ij}^+ \cup Y_{ij}^- \cup V(M^*_{ij})) $
;
$V(\mathcal {Q})\cap W \subseteq \bigcup _{i,j \in [k]} (Y_{ij}^+ \cup Y_{ij}^- \cup V(M^*_{ij})) $
; -
(iii′′) if
 $y^+\in Y_{ij}^+\setminus V^-(M^*)$
, then there exists
$y^+\in Y_{ij}^+\setminus V^-(M^*)$
, then there exists
 $u\in V_{*j}\setminus W$
such that the single edge
$u\in V_{*j}\setminus W$
such that the single edge
 $y^+u$
is a path in
$y^+u$
is a path in
 $\mathcal {Q}$
, and a similar statement for
$\mathcal {Q}$
, and a similar statement for
 $y^-\in Y_{ij}^-\setminus V^+(M^*)$
holds.
$y^-\in Y_{ij}^-\setminus V^+(M^*)$
holds.
Consider
![]() $i \in [k]$
. Recall that
$i \in [k]$
. Recall that
![]() $N^-_{F^*}(s_i) = \{s^*, t_i\}$
,
$N^-_{F^*}(s_i) = \{s^*, t_i\}$
,
![]() $ N^+_{F^*}(s_i) \subseteq X^+_{i*} \cup X^-$
, and each vertex in
$ N^+_{F^*}(s_i) \subseteq X^+_{i*} \cup X^-$
, and each vertex in
![]() $X^+$
has capacity one. We have
$X^+$
has capacity one. We have

and similarly we have
![]() $ f^*(t_it^*) + f^*(t_is_i) = \sum _{j \in [k]} e(\mathcal {Q}_{ji}) $
. Since
$ f^*(t_it^*) + f^*(t_is_i) = \sum _{j \in [k]} e(\mathcal {Q}_{ji}) $
. Since
![]() $f^*$
saturates the edges
$f^*$
saturates the edges
![]() $s^*s_i$
and
$s^*s_i$
and
![]() $t_it^*$
, we deduce that,
$t_it^*$
, we deduce that,
 $$ \begin{align*} \sum_{j \in [k]} e(\mathcal{Q}_{ij}) - \sum_{j \in [k]} e(\mathcal{Q}_{ji}) &=f^*(s^*s_i)-f^*(t_it^*) = w^*(s^*s_i)-w^*(t_it^*) \\ &=\max \{|V_{i*}| - |V_{*i}|, 0\}-\max \{|V_{*i}| - |V_{i*}|, 0\} = |V_{i*}|-|V_{*i}| \end{align*} $$
$$ \begin{align*} \sum_{j \in [k]} e(\mathcal{Q}_{ij}) - \sum_{j \in [k]} e(\mathcal{Q}_{ji}) &=f^*(s^*s_i)-f^*(t_it^*) = w^*(s^*s_i)-w^*(t_it^*) \\ &=\max \{|V_{i*}| - |V_{*i}|, 0\}-\max \{|V_{*i}| - |V_{i*}|, 0\} = |V_{i*}|-|V_{*i}| \end{align*} $$
implying that
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathcal {P}$
-balanced, as required. By applying Proposition 7.6 (with
$\mathcal {P}$
-balanced, as required. By applying Proposition 7.6 (with
![]() $d = 1$
and
$d = 1$
and
![]() $G^0=\mathcal {Q}$
), we may further assume that
$G^0=\mathcal {Q}$
), we may further assume that

We now check the moreover statement of the Lemma 6.1. If
![]() $\sum _{i,j \in [k] \colon i \ne j} |V_{ij}|> k^2\gamma n$
(that is, (m1) holds), then (7.10) implies that
$\sum _{i,j \in [k] \colon i \ne j} |V_{ij}|> k^2\gamma n$
(that is, (m1) holds), then (7.10) implies that
![]() $\bigcup _{i,j \in [k] \colon i \ne j} V_{ij} \setminus V(\mathcal {Q}) \ne \emptyset $
, so
$\bigcup _{i,j \in [k] \colon i \ne j} V_{ij} \setminus V(\mathcal {Q}) \ne \emptyset $
, so
![]() $\mathcal {Q}$
is non-trivial. Suppose that
$\mathcal {Q}$
is non-trivial. Suppose that
![]() $\sum _{i,j \in [k] \colon i \ne j} |V_{ij}| \le k^2 \gamma n$
and there exists
$\sum _{i,j \in [k] \colon i \ne j} |V_{ij}| \le k^2 \gamma n$
and there exists
![]() $v_0\in V_{i_0j_0}$
satisfying (m2). If
$v_0\in V_{i_0j_0}$
satisfying (m2). If
![]() $v_0 \notin V(\mathcal {Q})$
, then
$v_0 \notin V(\mathcal {Q})$
, then
![]() $\mathcal {Q}$
is non-trivial. So suppose that
$\mathcal {Q}$
is non-trivial. So suppose that
![]() $v_0 \in V(\mathcal {Q})$
. Since
$v_0 \in V(\mathcal {Q})$
. Since
![]() $v_0 \in W$
, by (ii
$v_0 \in W$
, by (ii
![]() $"$
) we must have
$"$
) we must have
![]() $v_0 \in Y_{ij}^+ \cup Y_{ij}^- \cup V(M_{ij}^*)$
for some
$v_0 \in Y_{ij}^+ \cup Y_{ij}^- \cup V(M_{ij}^*)$
for some
![]() $i,j \in [k]$
. This means that there is a flow through
$i,j \in [k]$
. This means that there is a flow through
![]() $v_0^-$
as
$v_0^-$
as
![]() $v_0^+ \notin V(F^*)$
. By (7.6),
$v_0^+ \notin V(F^*)$
. By (7.6),
![]() $v_0 \in Y_{ij_0}^-$
for some
$v_0 \in Y_{ij_0}^-$
for some
![]() $i \ne i_0$
. Also,
$i \ne i_0$
. Also,
![]() $v_0^+\notin V(F^*)$
implies that
$v_0^+\notin V(F^*)$
implies that
![]() $v_0\notin V^+(M^*)$
. By (iii
$v_0\notin V^+(M^*)$
. By (iii
![]() $"$
), we deduce that there exists
$"$
), we deduce that there exists
![]() $u \in V_{i*} \setminus W = V_{ii}$
such that
$u \in V_{i*} \setminus W = V_{ii}$
such that
![]() $uv_0$
is a path in
$uv_0$
is a path in
![]() $\mathcal {Q}$
. Note that
$\mathcal {Q}$
. Note that
![]() $uv_0$
is a path from
$uv_0$
is a path from
![]() $V_{ii} \subseteq V_{*i}$
to
$V_{ii} \subseteq V_{*i}$
to
![]() $V_{i_0j_0} \subseteq V_{i_0 *}$
. Hence
$V_{i_0j_0} \subseteq V_{i_0 *}$
. Hence
![]() $\mathcal {Q}$
is non-trivial, as required.
$\mathcal {Q}$
is non-trivial, as required.
Step 4: Define a distribution function on
![]() $\mathbf {X^+ \cup X^-}$
. For each
$\mathbf {X^+ \cup X^-}$
. For each
![]() $i \in [k]$
,
$i \in [k]$
,
![]() $x^+ \in X^+_{i*}$
and
$x^+ \in X^+_{i*}$
and
![]() $x^- \in X^-_{*i}$
,
$x^- \in X^-_{*i}$
,
![]() $j \in [k] \setminus \{ i\}$
, we set
$j \in [k] \setminus \{ i\}$
, we set
Given
![]() $x^+ \in X^+_{i*}$
, we ‘view’
$x^+ \in X^+_{i*}$
, we ‘view’
![]() $p_j({x^+})$
to be flow through
$p_j({x^+})$
to be flow through
![]() $x^+$
from
$x^+$
from
![]() $s_i$
to
$s_i$
to
![]() $t_j$
, and similarly for
$t_j$
, and similarly for
![]() $p_j({x^-})$
.
$p_j({x^-})$
.
Claim 7.11. For each
![]() $i \in [k]$
and
$i \in [k]$
and
![]() $x^+ \in X^+_{i*}$
,
$x^+ \in X^+_{i*}$
,
 $$ \begin{align*} \sum_{j \in [k] \setminus \{i\} } p_j({x^+}) \le 1 - \frac{d_{G^0}^+(x,V_{*i})}{d} + 6 k^3 \gamma^{1/3} < 1 \end{align*} $$
$$ \begin{align*} \sum_{j \in [k] \setminus \{i\} } p_j({x^+}) \le 1 - \frac{d_{G^0}^+(x,V_{*i})}{d} + 6 k^3 \gamma^{1/3} < 1 \end{align*} $$
and a similar statement holds for each
![]() $j \in [k]$
and
$j \in [k]$
and
![]() $x^- \in X^-_{*j}$
.
$x^- \in X^-_{*j}$
.
Proof of claim
We will only consider the case when
![]() $x^+ \in X^+_{i*}$
as the other case when
$x^+ \in X^+_{i*}$
as the other case when
![]() $x^- \in X^-_{*j}$
can be proved similarly. Since G is a subgraph of
$x^- \in X^-_{*j}$
can be proved similarly. Since G is a subgraph of
![]() $G^0$
, we have
$G^0$
, we have
 $$ \begin{align*} \sum_{j \in [k]\setminus\{i\} } d_{G_{ij}}^+(x^+) \le \sum_{j \in [k]\setminus\{i\} } d_{G_{ij}^0}^+(x^+) = d-d_{G^0}^+(x,V_{*i}). \end{align*} $$
$$ \begin{align*} \sum_{j \in [k]\setminus\{i\} } d_{G_{ij}}^+(x^+) \le \sum_{j \in [k]\setminus\{i\} } d_{G_{ij}^0}^+(x^+) = d-d_{G^0}^+(x,V_{*i}). \end{align*} $$
Hence
 $$ \begin{align*} \sum_{j \in [k]\setminus \{i\} } p_j({x^+}) & \le \sum_{j \in [k]\setminus \{i\} } \left( \frac{d_{G_{ij}}^+(x^+)}d + 6 k^2 \gamma^{1/3} \right) \le \frac{\sum_{j \in [k]\setminus \{i\}} d_{G_{ij}}^+(x^+)} d + 6 k^3 \gamma^{1/3}\\ & \le 1 - \frac{d_{G^0}^+(x,V_{*i})}{d} + 6 k^3 \gamma^{1/3} <1, \end{align*} $$
$$ \begin{align*} \sum_{j \in [k]\setminus \{i\} } p_j({x^+}) & \le \sum_{j \in [k]\setminus \{i\} } \left( \frac{d_{G_{ij}}^+(x^+)}d + 6 k^2 \gamma^{1/3} \right) \le \frac{\sum_{j \in [k]\setminus \{i\}} d_{G_{ij}}^+(x^+)} d + 6 k^3 \gamma^{1/3}\\ & \le 1 - \frac{d_{G^0}^+(x,V_{*i})}{d} + 6 k^3 \gamma^{1/3} <1, \end{align*} $$
where the last inequality holds as
![]() $d_{G^0}^+(x,V_{*i})\ge d/k$
by (i) and
$d_{G^0}^+(x,V_{*i})\ge d/k$
by (i) and
![]() $\gamma \ll 1/k$
.
$\gamma \ll 1/k$
.
Step 5: Defining fractional flow on
![]() $\mathbf {\mathcal {F}_0}$
. We first define the fractional flow f on
$\mathbf {\mathcal {F}_0}$
. We first define the fractional flow f on
![]() $\mathcal {F}$
as follows. For each
$\mathcal {F}$
as follows. For each
![]() $i,j \in [k]$
, we do the following
$i,j \in [k]$
, we do the following
-
• for each
 $x^+ \in X_{ij}^+ \subseteq V_{i*}$
, add a flow through
$x^+ \in X_{ij}^+ \subseteq V_{i*}$
, add a flow through
 $s_{i} x^+ t_{j} $
of value
$s_{i} x^+ t_{j} $
of value
 $p_j(x^+)$
;
$p_j(x^+)$
; -
• for each
 $x^- \in X_{ij}^- \subseteq V_{*j}$
, add a flow through
$x^- \in X_{ij}^- \subseteq V_{*j}$
, add a flow through
 $s_{i} x^- t_{j}$
of value
$s_{i} x^- t_{j}$
of value
 $p_i(x^-)$
;
$p_i(x^-)$
; -
• for each edge
 $e=uv \in M_{ij}$
, add a flow through
$e=uv \in M_{ij}$
, add a flow through
 $s_{i} u^+ v^- t_{j}$
of value
$s_{i} u^+ v^- t_{j}$
of value
 $6 k^2 \gamma ^{1/3}$
.
$6 k^2 \gamma ^{1/3}$
.
Our construction and Claim 7.11 imply that each vertex
![]() $v \in X^+ \cup X^- $
has a flow of value at most
$v \in X^+ \cup X^- $
has a flow of value at most
![]() $1$
through it. Thus f is indeed a fractional flow on
$1$
through it. Thus f is indeed a fractional flow on
![]() $\mathcal {F}$
. For each
$\mathcal {F}$
. For each
![]() $i,j \in [k]$
,
$i,j \in [k]$
,

Therefore,
 $$ \begin{align*} \sum_{i,j \in [k]} \max\{ e(G_{ij})/d - f_{ij}, 0 \} \le 50 k^{12} \gamma^{1/3} <1. \end{align*} $$
$$ \begin{align*} \sum_{i,j \in [k]} \max\{ e(G_{ij})/d - f_{ij}, 0 \} \le 50 k^{12} \gamma^{1/3} <1. \end{align*} $$
If there is no
![]() $v_0$
satisfying (m2), then
$v_0$
satisfying (m2), then
![]() $\mathcal {F}_0 = \mathcal {F}$
and we are done by Claim 7.10. If such a
$\mathcal {F}_0 = \mathcal {F}$
and we are done by Claim 7.10. If such a
![]() $v_0$
exists, then recall that
$v_0$
exists, then recall that
![]() $F_0$
is obtained from F removing the vertex
$F_0$
is obtained from F removing the vertex
![]() $v_0^+$
, the edge
$v_0^+$
, the edge
![]() $s_{i_0} v_0^-$
and edges in
$s_{i_0} v_0^-$
and edges in
![]() $E_F(X^+,v_0^-)$
. By repeated application of Proposition 7.2, we obtain a flow in
$E_F(X^+,v_0^-)$
. By repeated application of Proposition 7.2, we obtain a flow in
![]() $\mathcal {F}_0$
whose value is lower than that of f by at most
$\mathcal {F}_0$
whose value is lower than that of f by at most

Therefore,
![]() $\sum _{i,j \in [k]} \max \{ e(G_{ij})/d - f_{ij}, 0 \}$
is still less than
$\sum _{i,j \in [k]} \max \{ e(G_{ij})/d - f_{ij}, 0 \}$
is still less than
![]() $1$
. Hence we are done by Claim 7.10.
$1$
. Hence we are done by Claim 7.10.
8. Proof of Lemma 6.3
We begin with an outline of the proof of the Lemma 6.3. Let G and
![]() $\mathcal {P}$
be the digraph and vertex partition as in the statement of Lemma 6.3. Suppose, contrary to the lemma, that there is no non-trivial
$\mathcal {P}$
be the digraph and vertex partition as in the statement of Lemma 6.3. Suppose, contrary to the lemma, that there is no non-trivial
![]() $\mathcal {P}$
-balanced path system.
$\mathcal {P}$
-balanced path system.
Consider distinct
![]() $i,j \in [k]$
. Note that if there exist two vertex-disjoint edges
$i,j \in [k]$
. Note that if there exist two vertex-disjoint edges
![]() $e_1 \in E(G_{ij})$
and
$e_1 \in E(G_{ij})$
and
![]() $e_2 \in E(G_{ji})$
, then
$e_2 \in E(G_{ji})$
, then
![]() $\{e_1,e_2\}$
forms a non-trivial
$\{e_1,e_2\}$
forms a non-trivial
![]() $\mathcal {P}$
-balanced path system. Thus, if
$\mathcal {P}$
-balanced path system. Thus, if
![]() $e(G_{ij}), e(G_{ji}) \ge 3$
, then we may assume that there exists a vertex
$e(G_{ij}), e(G_{ji}) \ge 3$
, then we may assume that there exists a vertex
![]() $ w_{ij} \in V_{ii} \cup V_{jj}$
that is contained in all edges of
$ w_{ij} \in V_{ii} \cup V_{jj}$
that is contained in all edges of
![]() $G_{ij} \cup G_{ji}$
. Let H be the oriented graph on
$G_{ij} \cup G_{ji}$
. Let H be the oriented graph on
![]() $[k]$
where
$[k]$
where
![]() $ij \in E(H)$
if
$ij \in E(H)$
if
![]() $e(G_{ij}), e(G_{ji}) \ge 3$
and
$e(G_{ij}), e(G_{ji}) \ge 3$
and
![]() $w_{ij} \in V_{jj}$
; we give weight
$w_{ij} \in V_{jj}$
; we give weight
![]() $w(ij):=|E(G_{ij}\cup G_{ji})|$
to
$w(ij):=|E(G_{ij}\cup G_{ji})|$
to
![]() $ij$
.Footnote 8 It turns out that the underlying undirected graph of H is acyclic (see Claim 8.1) and that total weight of edges in H is almost equal to
$ij$
.Footnote 8 It turns out that the underlying undirected graph of H is acyclic (see Claim 8.1) and that total weight of edges in H is almost equal to
![]() $|\mathcal {B}(G, \mathcal {P})|$
(see (8.6)). Set
$|\mathcal {B}(G, \mathcal {P})|$
(see (8.6)). Set
![]() $w(i)=\sum _{j\in [k]}(w(ij)-w(ji))$
.
$w(i)=\sum _{j\in [k]}(w(ij)-w(ji))$
.
We focus on the
![]() $V_{ii}$
that are relatively small: let
$V_{ii}$
that are relatively small: let
![]() $c_i=qd+1-|V_{ii}|$
(where we set
$c_i=qd+1-|V_{ii}|$
(where we set
![]() $q=2$
if G is an oriented graph and
$q=2$
if G is an oriented graph and
![]() $q=1$
otherwise) and after relabelling indices assume
$q=1$
otherwise) and after relabelling indices assume
![]() $ |\{i \in [k]: c_i\geq 0\}| = [k_0]$
. We will lower and upper bound
$ |\{i \in [k]: c_i\geq 0\}| = [k_0]$
. We will lower and upper bound
![]() $\sum _{i\in [k_0]}w(i)$
. For the lower bound, we note that if
$\sum _{i\in [k_0]}w(i)$
. For the lower bound, we note that if
![]() $c_i>0$
then every vertex of
$c_i>0$
then every vertex of
![]() $V_{ii}$
has at least one edge from outside
$V_{ii}$
has at least one edge from outside
![]() $V_{ii}$
, and so we can lower bound
$V_{ii}$
, and so we can lower bound
![]() $w(i)$
in terms of
$w(i)$
in terms of
![]() $c_i$
for each
$c_i$
for each
![]() $i\in [k_0]$
(see (8.12)). For the upper bound, we note that
$i\in [k_0]$
(see (8.12)). For the upper bound, we note that
![]() $w(ij)$
can be upper bounded using (iii) (see (8.2)). Then, as H is acyclic (so has few edges), we are able to find a good upper bound for
$w(ij)$
can be upper bounded using (iii) (see (8.2)). Then, as H is acyclic (so has few edges), we are able to find a good upper bound for
![]() $\sum _{i\in [k_0]}w(i)$
by considering connected components (i.e., trees) in
$\sum _{i\in [k_0]}w(i)$
by considering connected components (i.e., trees) in
![]() $H[[k_0]]$
. Combining the lower and upper bounds, we obtain
$H[[k_0]]$
. Combining the lower and upper bounds, we obtain
![]() $\sum _{i\in [k_0]}c_i\leq k-k_0-1$
(see (8.15)) whereas (ii) implies
$\sum _{i\in [k_0]}c_i\leq k-k_0-1$
(see (8.15)) whereas (ii) implies
![]() $\sum _{i\in [k_0]}c_i>k-k_0$
, a contradiction.
$\sum _{i\in [k_0]}c_i>k-k_0$
, a contradiction.
Recall that for a digraph G and
![]() $A,B \subseteq V(G)$
not necessarily disjoint, we write
$A,B \subseteq V(G)$
not necessarily disjoint, we write
![]() $E_G(A,B):= \{ab \in E(G): a \in A, \; b \in B \}$
and
$E_G(A,B):= \{ab \in E(G): a \in A, \; b \in B \}$
and
![]() $e_G(A,B) := |E_G(A,B)|$
. We write
$e_G(A,B) := |E_G(A,B)|$
. We write
![]() $E_G(A)$
and
$E_G(A)$
and
![]() $e_G(A)$
for
$e_G(A)$
for
![]() $E_G(A,A)$
and
$E_G(A,A)$
and
![]() $e_G(A,A)$
, respectively.
$e_G(A,A)$
, respectively.
Proof of Lemma 6.3
Assume G and
![]() $\mathcal {P}$
satisfy (i)–(iii) in the statement of Lemma 6.3. Let
$\mathcal {P}$
satisfy (i)–(iii) in the statement of Lemma 6.3. Let
![]() $q =2$
if G is an oriented graph and
$q =2$
if G is an oriented graph and
![]() $q =1$
otherwise, so (ii) says that
$q =1$
otherwise, so (ii) says that
![]() $n<(qd + 1)k$
. We write
$n<(qd + 1)k$
. We write
![]() $V_i$
instead of
$V_i$
instead of
![]() $V_{ii}$
for
$V_{ii}$
for
![]() $i \in [k]$
, so that, for all distinct
$i \in [k]$
, so that, for all distinct
![]() $i,j\in [k]$
,
$i,j\in [k]$
,
![]() $G_{ij}$
becomes the bipartite digraph with vertex classes
$G_{ij}$
becomes the bipartite digraph with vertex classes
![]() $V_i$
and
$V_i$
and
![]() $V_j$
and edges given by the edges of G from
$V_j$
and edges given by the edges of G from
![]() $V_{i}$
to
$V_{i}$
to
![]() $V_{j}$
. In this context (where
$V_{j}$
. In this context (where
![]() $V_{ij}=\emptyset $
for all distinct
$V_{ij}=\emptyset $
for all distinct
![]() $i,j\in [k]$
),
$i,j\in [k]$
),
![]() $\mathcal {Q}$
is a
$\mathcal {Q}$
is a
![]() $\mathcal {P}$
-balanced path system if, for each
$\mathcal {P}$
-balanced path system if, for each
![]() $i\in [k]$
, the number of edges of
$i\in [k]$
, the number of edges of
![]() $\mathcal {Q}$
going into
$\mathcal {Q}$
going into
![]() $V_i$
is equal to the number of edges of
$V_i$
is equal to the number of edges of
![]() $\mathcal {Q}$
leaving
$\mathcal {Q}$
leaving
![]() $V_i$
. Also, a
$V_i$
. Also, a
![]() $\mathcal {P}$
-balanced path system is non-trivial if it has at least one path whose endpoints lie in distinct parts of the partition
$\mathcal {P}$
-balanced path system is non-trivial if it has at least one path whose endpoints lie in distinct parts of the partition
![]() $\mathcal {P}=\{V_i:i\in [k]\}$
. Now suppose for a contradiction that G does not contain any non-trivial
$\mathcal {P}=\{V_i:i\in [k]\}$
. Now suppose for a contradiction that G does not contain any non-trivial
![]() $\mathcal {P}$
-balanced path system with at most k edges.
$\mathcal {P}$
-balanced path system with at most k edges.
Claim 8.1. Let
![]() $H_0$
be a digraph on
$H_0$
be a digraph on
![]() $[k]$
such that
$[k]$
such that
![]() $ij \in E(H_0)$
if
$ij \in E(H_0)$
if
![]() $e(G_{ij}) \ge 3$
and
$e(G_{ij}) \ge 3$
and
![]() $i\neq j$
. Then
$i\neq j$
. Then
![]() $H_0$
does not have any directed cycle of length at least
$H_0$
does not have any directed cycle of length at least
![]() $3$
.
$3$
.
Proof of claim
Suppose to the contrary that C is such a cycle in
![]() $H_0$
. For each
$H_0$
. For each
![]() $ij \in E(C)$
, we pick an edge
$ij \in E(C)$
, we pick an edge
![]() $e_{ij}\in E(G_{ij})$
with
$e_{ij}\in E(G_{ij})$
with
![]() $ij \in E(C)$
and call the resulting subdigraph
$ij \in E(C)$
and call the resulting subdigraph
![]() $G^{\prime }$
. Note that
$G^{\prime }$
. Note that
![]() $G^{\prime }$
is
$G^{\prime }$
is
![]() $\mathcal {P}$
-balanced and has at most k edges; moreover it is either a cycle or a path system. If
$\mathcal {P}$
-balanced and has at most k edges; moreover it is either a cycle or a path system. If
![]() $G^{\prime }$
is a cycle, then pick an
$G^{\prime }$
is a cycle, then pick an
![]() $ij\in E(C)$
, and find
$ij\in E(C)$
, and find
![]() $e_{ij}^{\prime }\in E(G_{ij})$
with
$e_{ij}^{\prime }\in E(G_{ij})$
with
![]() $e_{ij}^{\prime }\neq e_{ij}$
. Write
$e_{ij}^{\prime }\neq e_{ij}$
. Write
![]() $G^{\prime \prime }=(G^{\prime }-\{e_{ij}\})\cup \{e_{ij}^{\prime }\}$
if
$G^{\prime \prime }=(G^{\prime }-\{e_{ij}\})\cup \{e_{ij}^{\prime }\}$
if
![]() $G^{\prime }$
is a cycle and
$G^{\prime }$
is a cycle and
![]() $G^{\prime \prime }=G^{\prime }$
otherwise. Note that
$G^{\prime \prime }=G^{\prime }$
otherwise. Note that
![]() $G^{\prime \prime }$
is a
$G^{\prime \prime }$
is a
![]() $\mathcal {P}$
-balanced path system. If
$\mathcal {P}$
-balanced path system. If
![]() $G^{\prime \prime }$
is a single path, then there exists
$G^{\prime \prime }$
is a single path, then there exists
![]() $t\in [k]$
such that the endpoints of
$t\in [k]$
such that the endpoints of
![]() $G^{\prime \prime }$
lies in
$G^{\prime \prime }$
lies in
![]() $V_{t}$
. Then, pick an
$V_{t}$
. Then, pick an
![]() $i^{\prime }j^{\prime }\in E(C)$
with
$i^{\prime }j^{\prime }\in E(C)$
with
![]() $i^{\prime },j^{\prime }\neq t$
, and find
$i^{\prime },j^{\prime }\neq t$
, and find
![]() $e_{i^{\prime }j^{\prime }}^{\prime }\in E(G_{i^{\prime }j^{\prime }})$
with
$e_{i^{\prime }j^{\prime }}^{\prime }\in E(G_{i^{\prime }j^{\prime }})$
with
![]() $e_{i^{\prime }j^{\prime }}^{\prime }\neq e_{ij}, e_{i^{\prime }j^{\prime }}$
. Write
$e_{i^{\prime }j^{\prime }}^{\prime }\neq e_{ij}, e_{i^{\prime }j^{\prime }}$
. Write
![]() $G^{\prime \prime \prime }=(G^{\prime \prime }-\{e_{i^{\prime }j^{\prime }}\})\cup \{e_{i^{\prime }j^{\prime }}^{\prime }\}$
if
$G^{\prime \prime \prime }=(G^{\prime \prime }-\{e_{i^{\prime }j^{\prime }}\})\cup \{e_{i^{\prime }j^{\prime }}^{\prime }\}$
if
![]() $G^{\prime \prime }$
is a single path and
$G^{\prime \prime }$
is a single path and
![]() $G^{\prime \prime \prime }=G^{\prime \prime }$
otherwise. Note that
$G^{\prime \prime \prime }=G^{\prime \prime }$
otherwise. Note that
![]() $G^{\prime \prime \prime }$
consists of at least two vertex-disjoint paths and that for any path in
$G^{\prime \prime \prime }$
consists of at least two vertex-disjoint paths and that for any path in
![]() $G^{\prime \prime \prime }$
, the endpoints lie in distinct parts of the partition
$G^{\prime \prime \prime }$
, the endpoints lie in distinct parts of the partition
![]() $\mathcal {P}=\{V_{i}:i\in [k]\}$
, so
$\mathcal {P}=\{V_{i}:i\in [k]\}$
, so
![]() $G^{\prime \prime \prime }$
is a non-trivial
$G^{\prime \prime \prime }$
is a non-trivial
![]() $\mathcal {P}$
-balanced path system with at most k edges, a contradiction.
$\mathcal {P}$
-balanced path system with at most k edges, a contradiction.
Claim 8.2. For all distinct
![]() $i,j \in [k]$
, if
$i,j \in [k]$
, if
![]() $e(G_{ij})\le 2$
, then
$e(G_{ij})\le 2$
, then
![]() $e(G_{ji})\le 2k^2$
.
$e(G_{ji})\le 2k^2$
.
Proof of claim
Suppose to the contrary and without loss of generality that
![]() $e(G_{21})\le 2$
and
$e(G_{21})\le 2$
and
![]() $e(G_{12})\ge 2k^2+1$
. Let
$e(G_{12})\ge 2k^2+1$
. Let
![]() $H_0$
be as defined in Claim 8.1, so
$H_0$
be as defined in Claim 8.1, so
![]() $12 \in E(H_0)$
and
$12 \in E(H_0)$
and
![]() $21\notin E(H_0)$
. Let A be the set of
$21\notin E(H_0)$
. Let A be the set of
![]() $i\in [k]$
such that
$i\in [k]$
such that
![]() $H_0$
contains a directed path from
$H_0$
contains a directed path from
![]() $1$
to i starting with the edge
$1$
to i starting with the edge
![]() $12$
, where we a priori allow
$12$
, where we a priori allow
![]() $1 \in A$
(i.e., resulting from a closed path). Let
$1 \in A$
(i.e., resulting from a closed path). Let
![]() $B=[k]\setminus A$
. It is clear from the definition that
$B=[k]\setminus A$
. It is clear from the definition that
![]() $2\in A$
, and by Claim 8.1 and since
$2\in A$
, and by Claim 8.1 and since
![]() $21\notin E(H_0)$
we have
$21\notin E(H_0)$
we have
![]() $1\in B$
. Note that by the definition of A, there are no edges in
$1\in B$
. Note that by the definition of A, there are no edges in
![]() $E_{H_0}(A,B)$
so that
$E_{H_0}(A,B)$
so that
![]() $e(G_{ij})\le 2$
for all
$e(G_{ij})\le 2$
for all
![]() $ij\in A\times B$
. Together with the regularity of G, we have
$ij\in A\times B$
. Together with the regularity of G, we have
 $$ \begin{align*} 2k^2\ge \sum_{ij\in A\times B}e(G_{ij})=\sum_{ij\in B\times A} e(G_{ij}) \ge e(G_{12})\ge 2k^2+1, \end{align*} $$
$$ \begin{align*} 2k^2\ge \sum_{ij\in A\times B}e(G_{ij})=\sum_{ij\in B\times A} e(G_{ij}) \ge e(G_{12})\ge 2k^2+1, \end{align*} $$
which is a contradiction.
Let
![]() $H^*$
be the graph on
$H^*$
be the graph on
![]() $[k]$
such that
$[k]$
such that
![]() $ij \in E(H^*)$
if
$ij \in E(H^*)$
if
![]() $e(G_{ij}), e(G_{ji}) \ge 3$
(i.e.,
$e(G_{ij}), e(G_{ji}) \ge 3$
(i.e.,
![]() $H^*$
is the graph obtained from
$H^*$
is the graph obtained from
![]() $H_0$
by deleting all the edges which do not lie in a directed
$H_0$
by deleting all the edges which do not lie in a directed
![]() $2$
-cycle and by making each directed
$2$
-cycle and by making each directed
![]() $2$
-cycle into an undirected edge). By Claim 8.1,
$2$
-cycle into an undirected edge). By Claim 8.1,
![]() $H^*$
is acyclic. Consider distinct
$H^*$
is acyclic. Consider distinct
![]() $i,j \in [k]$
. Note that there do not exist disjoint edges
$i,j \in [k]$
. Note that there do not exist disjoint edges
![]() $e_1, e_2$
with
$e_1, e_2$
with
![]() $e_1 \in E(G_{ij})$
and
$e_1 \in E(G_{ij})$
and
![]() $e_2 \in E(G_{ji})$
because otherwise
$e_2 \in E(G_{ji})$
because otherwise
![]() $\{e_1,e_2\}$
would form a non-trivial
$\{e_1,e_2\}$
would form a non-trivial
![]() $\mathcal {P}$
-balanced path system. Thus if
$\mathcal {P}$
-balanced path system. Thus if
![]() $ij \in E(H^*)$
(that is,
$ij \in E(H^*)$
(that is,
![]() $e(G_{ij}) , e(G_{ji})\ge 3$
), then there exists a vertex
$e(G_{ij}) , e(G_{ji})\ge 3$
), then there exists a vertex
![]() $w_{ij}\in V_{i} \cup V_j$
that is contained in all edges of
$w_{ij}\in V_{i} \cup V_j$
that is contained in all edges of
![]() $G_{ij} \cup G_{ji}$
. So, we have
$G_{ij} \cup G_{ji}$
. So, we have
If
![]() $ij \not \in E(H^*)$
, then
$ij \not \in E(H^*)$
, then
![]() $\min \{e(G_{ij}), e(G_{ji})\}\le 2$
and by Claim 8.2, we obtain
$\min \{e(G_{ij}), e(G_{ji})\}\le 2$
and by Claim 8.2, we obtain
as
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $d>165k^5$
. Hence we have
$d>165k^5$
. Hence we have
Recall that
![]() $q =2$
if G is an oriented graph, and
$q =2$
if G is an oriented graph, and
![]() $q =1$
otherwise. Note that, if
$q =1$
otherwise. Note that, if
![]() $|V_i|\le qd+1$
for some
$|V_i|\le qd+1$
for some
![]() $i\in [k]$
, then
$i\in [k]$
, then

Hence, for all
![]() $i\in [k]$
,
$i\in [k]$
,
We now orient
![]() $H^*$
to obtain an oriented graph H on
$H^*$
to obtain an oriented graph H on
![]() $[k]$
as follows. Recall that if
$[k]$
as follows. Recall that if
![]() $ij \in E(H^*)$
, then there exists a vertex
$ij \in E(H^*)$
, then there exists a vertex
![]() $w_{ij} \in V_i \cup V_j$
contained in all edges of
$w_{ij} \in V_i \cup V_j$
contained in all edges of
![]() $E(G_{ij}) \cup E(G_{ji})$
. We orient from i to j if
$E(G_{ij}) \cup E(G_{ji})$
. We orient from i to j if
![]() $w_{ij} \in V_j$
.
$w_{ij} \in V_j$
.
Let W be the set of
![]() $w_{ij}$
and
$w_{ij}$
and
![]() $W_i = W \cap V_i$
for all
$W_i = W \cap V_i$
for all
![]() $i \in [k]$
. Let
$i \in [k]$
. Let
![]() $V_i^{\prime }=V_i\setminus W_i$
. Note that
$V_i^{\prime }=V_i\setminus W_i$
. Note that
Recall that
![]() $\mathcal {B}(G, \mathcal {P})=\bigcup _{i,j\in [k]:\,i\neq j}G_{ij}$
. Let
$\mathcal {B}(G, \mathcal {P})=\bigcup _{i,j\in [k]:\,i\neq j}G_{ij}$
. Let
![]() $G^* = \bigcup _{i,j \in [k]}G^*_{ij}$
where
$G^* = \bigcup _{i,j \in [k]}G^*_{ij}$
where
![]() $G^*_{ij}$
is the subdigraph of
$G^*_{ij}$
is the subdigraph of
![]() $\mathcal {B}(G, \mathcal {P})$
consisting of the edges (in both directions) between
$\mathcal {B}(G, \mathcal {P})$
consisting of the edges (in both directions) between
![]() $V_i^{\prime }$
and
$V_i^{\prime }$
and
![]() $w_{ij}$
if
$w_{ij}$
if
![]() $ij\in E(H)$
and
$ij\in E(H)$
and
![]() $G^*_{ij} = \emptyset $
otherwise.Footnote 9 Note that
$G^*_{ij} = \emptyset $
otherwise.Footnote 9 Note that
![]() $G^*_{ij}$
is a subdigraph of
$G^*_{ij}$
is a subdigraph of
![]() $G_{ij}\cup G_{ji}$
whenever
$G_{ij}\cup G_{ji}$
whenever
![]() $ij\in E(H)$
and
$ij\in E(H)$
and
![]() $G^*_{ij}=\emptyset $
otherwise. Therefore,
$G^*_{ij}=\emptyset $
otherwise. Therefore,
 $$ \begin{align} e( G^*_{ij} ) \begin{cases} \le e(G_{ij} \cup G_{ji}) & \text{ if }ij \in E(H); \\ = 0 & \text{ if }ij \notin E(H). \end{cases} \end{align} $$
$$ \begin{align} e( G^*_{ij} ) \begin{cases} \le e(G_{ij} \cup G_{ji}) & \text{ if }ij \in E(H); \\ = 0 & \text{ if }ij \notin E(H). \end{cases} \end{align} $$
Hence, we deduce that

For
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $\overline {V_i} = V(G) \setminus V_i$
. Since all edges in
$\overline {V_i} = V(G) \setminus V_i$
. Since all edges in
![]() $G^*$
contain a vertex in W and
$G^*$
contain a vertex in W and
![]() $G^*[W] \cup \bigcup _{i \in [k]}G^*_{ii}$
is empty, we have for all
$G^*[W] \cup \bigcup _{i \in [k]}G^*_{ii}$
is empty, we have for all
![]() $i \in [k]$
,
$i \in [k]$
,
 $$ \begin{align} \sum_{j\in[k]}e(G^*_{ij})=\sum_{j\in[k],\,ij\in E(H)}\bigg(e_{G^*}(V_i^{\prime},w_{ij})+e_{G^*}(w_{ij},V_i^{\prime})\bigg)=e_{G^*}(V_i^{\prime},\overline{V_i})+e_{G^*}(\overline{V_i},V_i^{\prime}) \end{align} $$
$$ \begin{align} \sum_{j\in[k]}e(G^*_{ij})=\sum_{j\in[k],\,ij\in E(H)}\bigg(e_{G^*}(V_i^{\prime},w_{ij})+e_{G^*}(w_{ij},V_i^{\prime})\bigg)=e_{G^*}(V_i^{\prime},\overline{V_i})+e_{G^*}(\overline{V_i},V_i^{\prime}) \end{align} $$
and, for all
![]() $j \in [k]$
,
$j \in [k]$
,
 $$ \begin{align} \sum_{i\in[k]}e(G^*_{ij})=\sum_{i\in[k],\,ij\in E(H)}\bigg(e_{G^*}(V_i',w_{ij})+e_{G^*}(w_{ij},V_i')\bigg)= e_{G^*}(\overline{V_j},W_j)+e_{G^*}(W_j,\overline{V_j}). \end{align} $$
$$ \begin{align} \sum_{i\in[k]}e(G^*_{ij})=\sum_{i\in[k],\,ij\in E(H)}\bigg(e_{G^*}(V_i',w_{ij})+e_{G^*}(w_{ij},V_i')\bigg)= e_{G^*}(\overline{V_j},W_j)+e_{G^*}(W_j,\overline{V_j}). \end{align} $$
We also need the following inequality
Now, let
![]() $ k_0 = |\{i \in [k]: |V_i| \le q d+1\}|$
. Note that
$ k_0 = |\{i \in [k]: |V_i| \le q d+1\}|$
. Note that
![]() $k_0>0$
since
$k_0>0$
since
![]() $n<(qd+1)k$
by (ii). Without loss of generality,
$n<(qd+1)k$
by (ii). Without loss of generality,
For
![]() $i \in [k_0]$
,
$i \in [k_0]$
,

Then,

and a similar inequality holds for
![]() $e_G ( \overline {V_{i}},V_i' )$
. Hence, for
$e_G ( \overline {V_{i}},V_i' )$
. Hence, for
![]() $i \in [k_0]$
,
$i \in [k_0]$
,
Let
![]() $\mathcal {I}$
be the set of all connected components I in
$\mathcal {I}$
be the set of all connected components I in
![]() $H^* \left [ [k_0] \right ]$
with
$H^* \left [ [k_0] \right ]$
with
![]() $\sum _{ i \in I} (qd +1 - |V_i| )>0$
.Footnote 10 Such
$\sum _{ i \in I} (qd +1 - |V_i| )>0$
.Footnote 10 Such
![]() $\mathcal {I}$
is non empty as
$\mathcal {I}$
is non empty as
![]() $n < (qd +1) k $
by (ii). We have that
$n < (qd +1) k $
by (ii). We have that
 $$ \begin{align} \sum_{i \in [k_0]} (qd +1 - |V_i| ) = \sum_{I\in\mathcal{I}} \sum_{ i \in I} (qd +1 - |V_i| ). \end{align} $$
$$ \begin{align} \sum_{i \in [k_0]} (qd +1 - |V_i| ) = \sum_{I\in\mathcal{I}} \sum_{ i \in I} (qd +1 - |V_i| ). \end{align} $$
Recall that
![]() $H^*$
is acyclic and H is an orientation of
$H^*$
is acyclic and H is an orientation of
![]() $H^*$
. Note that for each
$H^*$
. Note that for each
![]() $I\in \mathcal {I}$
,
$I\in \mathcal {I}$
,
![]() $H[I]$
is an oriented tree and
$H[I]$
is an oriented tree and
![]() $E_H ( I, [k]\setminus [k_0] ) = E_H ( I,[k] ) \setminus E_H (I)$
. Therefore, for each
$E_H ( I, [k]\setminus [k_0] ) = E_H ( I,[k] ) \setminus E_H (I)$
. Therefore, for each
![]() $I\in \mathcal {I}$
,
$I\in \mathcal {I}$
,

After rearranging, for each
![]() $I\in \mathcal {I}$
, we have
$I\in \mathcal {I}$
, we have
 $$ \begin{align*} e_H(I,[k]\setminus [k_0] ) &\ge \frac{2}{2-1/k} \sum_{ i \in I} (qd +1 - |V_i| ) - \frac{165 k^4}{(2-1/k)d} \\[5pt] &= \sum_{ i \in I}(qd +1 - |V_i| )+\frac{1}{2k-1}\sum_{ i \in I}(qd +1 - |V_i| ) - \frac{165 k^5}{(2k-1)d}\\[5pt] &\ge \sum_{ i \in I} (qd +1 - |V_i| )+\frac{1}{2k-1}-\frac{165 k^5}{(2k-1)d}>\sum_{ i \in I} (qd +1 - |V_i| ) \end{align*} $$
$$ \begin{align*} e_H(I,[k]\setminus [k_0] ) &\ge \frac{2}{2-1/k} \sum_{ i \in I} (qd +1 - |V_i| ) - \frac{165 k^4}{(2-1/k)d} \\[5pt] &= \sum_{ i \in I}(qd +1 - |V_i| )+\frac{1}{2k-1}\sum_{ i \in I}(qd +1 - |V_i| ) - \frac{165 k^5}{(2k-1)d}\\[5pt] &\ge \sum_{ i \in I} (qd +1 - |V_i| )+\frac{1}{2k-1}-\frac{165 k^5}{(2k-1)d}>\sum_{ i \in I} (qd +1 - |V_i| ) \end{align*} $$
as
![]() $\sum _{ i \in I} (qd +1 - |V_i| )\ge 1$
and
$\sum _{ i \in I} (qd +1 - |V_i| )\ge 1$
and
![]() $d>165k^5$
. Hence, we have
$d>165k^5$
. Hence, we have

Recall that H is an oriented forest and so
![]() $H[I]$
is an oriented tree for all
$H[I]$
is an oriented tree for all
![]() $I \in \mathcal {I}$
. Then,
$I \in \mathcal {I}$
. Then,
 $$ \begin{align*} \sum_{I\in \mathcal{I}} e_H (I,[k]\setminus [k_0] ) & \le e_{H} \left( \left([k]\setminus[k_0]\right)\cup \bigcup_{I\in \mathcal{I}} I \right) - \sum_{I\in \mathcal{I}}e_H(I) \nonumber \\ &\le \left( \left(k-k_0 +\sum_{I\in \mathcal{I}}|I|\right) - 1 \right)-\sum_{I\in \mathcal{I}}\left(|I|-1\right) = k-k_0+|\mathcal{I}|-1. \nonumber \end{align*} $$
$$ \begin{align*} \sum_{I\in \mathcal{I}} e_H (I,[k]\setminus [k_0] ) & \le e_{H} \left( \left([k]\setminus[k_0]\right)\cup \bigcup_{I\in \mathcal{I}} I \right) - \sum_{I\in \mathcal{I}}e_H(I) \nonumber \\ &\le \left( \left(k-k_0 +\sum_{I\in \mathcal{I}}|I|\right) - 1 \right)-\sum_{I\in \mathcal{I}}\left(|I|-1\right) = k-k_0+|\mathcal{I}|-1. \nonumber \end{align*} $$
Together with (8.14), we have
 $$ \begin{align} \sum_{ i \in [k_0]} (qd +1 - |V_i| ) \le k-k_0-1. \end{align} $$
$$ \begin{align} \sum_{ i \in [k_0]} (qd +1 - |V_i| ) \le k-k_0-1. \end{align} $$
Finally

a contradiction to property (ii) of Lemma 6.3. This completes the proof of the lemma.
9. Conclusion
9.1. Path cover for (non-regular) graphs
Magnant, Wang and Yuan [Reference Magnant, Wang and Yuan29] gave a stronger version of Conjecture 1.5. Recall that
![]() $\pi (G)$
is the minimum number of vertex-disjoint paths needed to cover G.
$\pi (G)$
is the minimum number of vertex-disjoint paths needed to cover G.
Conjecture 9.1 (Magnant, Wang and Yuan [Reference Magnant, Wang and Yuan29])
If G is a graph on n vertices with
![]() $\Delta (G) = \Delta $
and
$\Delta (G) = \Delta $
and
![]() $\delta (G) = \delta $
, then
$\delta (G) = \delta $
, then
![]() $\pi (G)\leq \max \{ n/(\delta +1) , (\Delta - \delta ) n / (\Delta + \delta ) \}$
.
$\pi (G)\leq \max \{ n/(\delta +1) , (\Delta - \delta ) n / (\Delta + \delta ) \}$
.
The bound is tight by considering a disjoint union of
![]() $K_{\delta +1}$
or a disjoint union of
$K_{\delta +1}$
or a disjoint union of
![]() $K_{\delta , \Delta }$
. The conjecture holds if
$K_{\delta , \Delta }$
. The conjecture holds if
![]() $\delta \le 2$
[Reference Magnant, Wang and Yuan29] and when
$\delta \le 2$
[Reference Magnant, Wang and Yuan29] and when
![]() $\Delta \ge 2 \delta $
[Reference Kouider and Zamime20]. Naturally, one can ask for the directed or oriented analogues.
$\Delta \ge 2 \delta $
[Reference Kouider and Zamime20]. Naturally, one can ask for the directed or oriented analogues.
9.2. Edge-disjoint cycles
In a weaker version of the problem that we have considered, one is interested in finding edge-disjoint cycles whose union covers all the vertices. As a generalization of Dirac’s theorem, it was conjectured by Enomoto, Kaneko and Tuza [Reference Enomoto, Kaneko and Tuza8] that if a graph G on n vertices has minimum degree at least
![]() $n/k$
, then
$n/k$
, then
![]() $V(G)$
can be covered by
$V(G)$
can be covered by
![]() $k-1$
edge-disjoint cycles. The case
$k-1$
edge-disjoint cycles. The case
![]() $k=3$
was also proved in [Reference Enomoto, Kaneko and Tuza8]. The conjecture was proved for
$k=3$
was also proved in [Reference Enomoto, Kaneko and Tuza8]. The conjecture was proved for
![]() $2$
-connected graphs [Reference Kouider18], and has been completely resolved in [Reference Kouider and Lonc19]. Later, Balogh, Mousset and Skokan [Reference Balogh, Mousset and Skokan3] obtained a stability result, showing that every graph on n vertices with minimum degree nearly
$2$
-connected graphs [Reference Kouider18], and has been completely resolved in [Reference Kouider and Lonc19]. Later, Balogh, Mousset and Skokan [Reference Balogh, Mousset and Skokan3] obtained a stability result, showing that every graph on n vertices with minimum degree nearly
![]() $n/k$
has a special structure if it does not have
$n/k$
has a special structure if it does not have
![]() $k-1$
edge-disjoint cycles covering all vertices. One can ask the same question for digraphs as a generalization of Ghoulia-Houri’s theorem [Reference Ghouila-Houri12], and Theorem 1.3 answers it affirmatively for regular digraphs:
$k-1$
edge-disjoint cycles covering all vertices. One can ask the same question for digraphs as a generalization of Ghoulia-Houri’s theorem [Reference Ghouila-Houri12], and Theorem 1.3 answers it affirmatively for regular digraphs:
Conjecture 9.2. Let
![]() $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
![]() $k\geq 2$
. If G is a digraph on n vertices with minimum semi-degree at least
$k\geq 2$
. If G is a digraph on n vertices with minimum semi-degree at least
![]() $n/k$
, then
$n/k$
, then
![]() $V(G)$
can be covered by
$V(G)$
can be covered by
![]() $k-1$
edge-disjoint cycles.
$k-1$
edge-disjoint cycles.
9.3. Connectivity and regularity
Jackson’s conjecture states that imposing regularity on an oriented graph reduces the degree threshold for Hamiltonicity. One might hope that imposing connectivity on regular oriented graphs can reduce the degree threshold for Hamiltonicity. We refer the reader to [Reference Lo, Patel and Yıldız27, Sections 1 and 7] for history and conjectures on Hamiltonicity in regular (directed or oriented) graphs with given connectivity.
Similarly, in the setting of cycle partitions, one might hope that connectivity in addition to regularity might reduce the upper bound in Conjecture 1.5. In the sparse setting, Reed [Reference Reed31] proved that every
![]() $3$
-regular connected n-vertex graph can be covered by at most
$3$
-regular connected n-vertex graph can be covered by at most
![]() $\lceil n/9 \rceil $
vertex-disjoint paths, and conjectured that it suffices to use
$\lceil n/9 \rceil $
vertex-disjoint paths, and conjectured that it suffices to use
![]() $\lceil n/10 \rceil $
paths if connectivity is replaced by
$\lceil n/10 \rceil $
paths if connectivity is replaced by
![]() $2$
-connectivity. Recall that Conjecture 1.5 gives the upper bound of
$2$
-connectivity. Recall that Conjecture 1.5 gives the upper bound of
![]() $n/4$
for
$n/4$
for
![]() $3$
-regular graphs (that are not necessarily connected). Yu [Reference Yu36] recently verified Reed’s conjecture and gave an example of a (2-connected) d-regular graph on n vertices which requires at least
$3$
-regular graphs (that are not necessarily connected). Yu [Reference Yu36] recently verified Reed’s conjecture and gave an example of a (2-connected) d-regular graph on n vertices which requires at least
![]() $\approx n/(d+4)$
paths for
$\approx n/(d+4)$
paths for
![]() $d\ge 13$
. It would be interesting to investigate the general relationship between the degree and connectivity of a regular (di)graph or oriented graph that guarantees a small number of vertex-disjoint cycles that cover all the vertices.
$d\ge 13$
. It would be interesting to investigate the general relationship between the degree and connectivity of a regular (di)graph or oriented graph that guarantees a small number of vertex-disjoint cycles that cover all the vertices.
Competing interest
The authors have no competing interests to declare.
Financial support
A. Lo was partially supported by EPSRC, grant no. EP/V002279/1 and EP/V048287/1. V. Patel was supported by the Netherlands Organisation for Scientific Research (NWO) through the Gravitation Programme Networks (024.002.003). M.A. Yıldız was supported by a Marie Skłodowska-Curie Action from the EC (COFUND grant no. 945045) and by the NWO Gravitation project NETWORKS (grant no. 024.002.003).
Data availability statement
There are no additional data beyond that contained within the main manuscript.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Author contributions
All authors contributed equally to the paper.