Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-29T11:10:01.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper, down, two-sided Lorenz attractor, collisions, merging, and switching

Part of: Dynamical systems with hyperbolic behavior Local and nonlocal bifurcation theory Dynamical problems Smooth dynamical systems: general theory

Published online by Cambridge University Press:  21 February 2024

DIEGO BARROS ,
CHRISTIAN BONATTI  and
MARIA JOSÉ PACIFICO
DIEGO BARROS
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil (e-mail: [email protected])
CHRISTIAN BONATTI
Affiliation:
Institut de Mathématiques de Bourgogne, CNRS, Université de Bourgogne, Dijon, France (e-mail: [email protected])
MARIA JOSÉ PACIFICO*
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a modified version of the well-known geometric Lorenz attractor. It consists of a 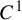$C^1$ open set ${\mathcal O}$ of vector fields in 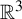${\mathbb R}^3$ having an attracting region 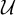${\mathcal U}$ satisfying three properties. Namely, a unique singularity 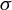$\sigma $; a unique attractor 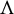$\Lambda $ including the singular point and the maximal invariant in 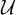${\mathcal U}$ has at most two chain recurrence classes, which are 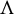$\Lambda $ and (at most) one hyperbolic horseshoe. The horseshoe and the singular attractor have a collision along with the union of 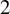$2$ codimension 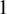$1$ submanifolds which split ${\mathcal O}$ into three regions. By crossing this collision locus, the attractor and the horseshoe may merge into a two-sided Lorenz attractor, or they may exchange their nature: the Lorenz attractor expels the singular point 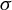$\sigma $ and becomes a horseshoe, and the horseshoe absorbs 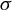$\sigma $ becoming a Lorenz attractor.

Keywords

Lorenz-like atractorsstrange attractorssingular flowssingular hyperbolic attractors

MSC classification

Primary: 37C10: Vector fields, flows, ordinary differential equations 37D45: Strange attractors, chaotic dynamics 37G35: Attractors and their bifurcations
Secondary: 74H60: Dynamical bifurcation
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 10 , October 2024 , pp. 2737 - 2781
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Afraimovich, V. S., Bykov, V. V. and Shil’nikov, L. P.. On the origin and structure of the Lorenz attractor. Akad. Nauk SSSR Doclady 234 (1977), 336–339.Google Scholar
Afraimovich, V. S., Bykov, V. V. and Shil’nikov, L. P.. On attracting structurally unstable limit sets of Lorenz attractor type. Tr. Moskov. Mat. Obshch. 44 (1982), 150–212 (in Russian).Google Scholar
Afraimovich, V. S. and Pesin, Y.. The dimension of Lorenz type attractors. Sov. Math. Phys. Rev. 6 (1983), 169–241.Google Scholar
Araújo, V.. On the statistical stability of families of attracting sets and the contracting Lorenz attractor. J. Stat. Phys. 182 (2021), 53.10.1007/s10955-021-02729-xCrossRefGoogle Scholar
Araújo, V., Galatolo, S. and Pacifico, M. J.. Statistical properties of Lorenz-like flows, recent developments and perspectives. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 24 (2014), 1430028.10.1142/S0218127414300286CrossRefGoogle Scholar
Araújo, V. and Melbourne, I.. Exponential decay of correlations for nonuniformly hyperbolic flows with a ${C}^{1+\alpha }$ stable foliation, including the classical Lorenz attractor. Ann. Henri Poincaré 17 (2016), 2975–3004.10.1007/s00023-016-0482-9CrossRefGoogle Scholar
Araújo, V. and Melbourne, I.. Existence and smoothness of the stable foliation for sectional hyperbolic attractors. Bull. Lond. Math. Soc. 49 (2017), 351–367.10.1112/blms.12037CrossRefGoogle Scholar
Araújo, V., Melbourne, I. and Varandas, P.. Rapid mixing for the Lorenz attractor and statistical limit laws for their time-1 maps. Comm. Math. Phys. 340 (2015), 901–938.10.1007/s00220-015-2471-0CrossRefGoogle Scholar
Araújo, V. and Pacifico, M. J.. Three-Dimensional Flows (Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics, 53). Springer Science & Business Media, Berlin, 2010.10.1007/978-3-642-11414-4CrossRefGoogle Scholar
Araújo, V. and Pacifico, M. J.. Lorenz-like chaotic attractors revised. Dynamics, Games and Science I (Springer Proceedings in Mathematics, 1). Ed. Peixoto, M. M., Pinto, A. A. and Rand, D. A.. Springer, Heidelberg, 2011, pp. 61–79.10.1007/978-3-642-11456-4_6CrossRefGoogle Scholar
Araújo, V., Pacifico, M. J., Pujals, P. and Viana, M.. Singular-hyperbolic attractors are chaotic. Trans. Amer. Math. Soc. 361 (2009), 2431–2485.10.1090/S0002-9947-08-04595-9CrossRefGoogle Scholar
Araújo, V. and Varandas, P.. Robust exponential decay of correlations for singular-flows. Comm. Math. Phys. 311 (2012), 215–246.10.1007/s00220-012-1445-8CrossRefGoogle Scholar
Bumimovich, L. and Sinai, Y.. Stochasticity of the attractor in the Lorenz model. Nonlinear Waves (Proceeding of Winter School, Gorki, 1977). Ed. Gaponov-Grekhov, A. V.. Nauka, Moscow, 1979, pp. 212–226.Google Scholar
Conley, C.. Some aspects of the qualitative theory of differential equations. Dynamical Systems (Proceedings of the International Symposium, Brown University, Providence, RI, 1974). Ed. Cesari, L., Hale, J. K. and Lasalle, J. P.. Vol. I. Academic Press, New York, 1976, pp. 1012.Google Scholar
Díaz, L.. Robust nonhyperbolic dynamics and heterodimensional cycles. Ergod. Th. & Dynam. Sys. 15 (1995), 291–315.10.1017/S0143385700008385CrossRefGoogle Scholar
Galatolo, S. and Nisoli, I.. Rigorous computation of invariant measures and fractal dimension for maps with contracting fibers: 2D Lorenz-like maps. Ergod. Th. & Dynam. Sys. 36(6) (2016), 1865–1891.10.1017/etds.2014.145CrossRefGoogle Scholar
Galatolo, S., Nisoli, I. and Pacifico, M. J.. Decay of correlations, quantitative recurrence and logarithm law for contracting Lorenz attractors. J. Stat. Phys. 170(5) (2018), 862–882.10.1007/s10955-018-1972-6CrossRefGoogle Scholar
Galatolo, S. and Pacifico, M. J.. Lorenz-like flows: exponential decay of correlations for the Poincaré map, logarithm law, quantitative recurrence. Ergod. Th. & Dynam. Sys. 30 (2010), 1703–1737.10.1017/S0143385709000856CrossRefGoogle Scholar
Gonchenko, S., Karatetskaia, E., Kazakov, A. and Kruglov, V.. Conjoined Lorenz twins-a new pseudohyperbolic attractor in three-dimensional maps and flows. Chaos 32(12) (2022), Paper no. 121107, 13pp.10.1063/5.0123426CrossRefGoogle ScholarPubMed
Gonchenko, S. V., Shilnikov, L. P. and Turaev, D.. On global bifurcations in three-dimensional diffeomorphisms leading to wild Lorenz-like attractors. Regul. Chaotic Dyn. 14(1) (2009), 137–147.10.1134/S1560354709010092CrossRefGoogle Scholar
Guckenheimer, J.. A strange, strange attractor. The Hopf Bifurcation and Its Applications. Ed. Marsden, J. E. and McCracken, M.. Springer, New York, 1976, pp. 368–381.10.1007/978-1-4612-6374-6_25CrossRefGoogle Scholar
Guckenheimer, J. and Holmes, P.. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Applied Mathematical Sciences, 42). Springer, New York, 1983.10.1007/978-1-4612-1140-2CrossRefGoogle Scholar
Guckenheimer, J. and Williams, R. F.. Structural stability of Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 59–72.10.1007/BF02684769CrossRefGoogle Scholar
Hartman, P.. Ordinary Differential Equations (Classics in Applied Mathematics, 38). Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2002; corrected reprint of the second (1982) edition.10.1137/1.9780898719222CrossRefGoogle Scholar
Hassard, B., Hastings, S., Troy, W. and Zhang, J.. A computer proof that the Lorenz equations have “chaotic” solutions. Appl. Math. Lett. 7 (1994), 79–83.10.1016/0893-9659(94)90058-2CrossRefGoogle Scholar
Hastings, S. and Troy, W.. A shooting approach to the Lorenz equations. Bull. Amer. Math. Soc. 27 (1992), 298–303.10.1090/S0273-0979-1992-00327-0CrossRefGoogle Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer-Verlag, Berlin, 1977.10.1007/BFb0092042CrossRefGoogle Scholar
Kazakov, A.. On bifurcations of Lorenz attractors in the Lyubimov–Zaks model. Chaos 31(9) (2021), 093118.10.1063/5.0058585CrossRefGoogle ScholarPubMed
Li, D. and Turaev, D.. Persistent heterodimensional cycles in periodic perturbations of Lorenz-like attractors. Nonlinearity 33 (2020), 971–1015.10.1088/1361-6544/ab5921CrossRefGoogle Scholar
Lorenz, E. N.. Deterministic nonperiodic flow. J. Atmos. Sci. 20 (1963), 130–141.10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;22.0.CO;2>CrossRefGoogle Scholar
Luzzatto, S., Melbourne, I. and Paccaut, F.. The Lorenz attractor is mixing. Comm. Math. Phys. 260 (2005), 393–401.10.1007/s00220-005-1411-9CrossRefGoogle Scholar
Lyubimov, D. V. and Zaks, M. A.. Two mechanisms of the transition to chaos in finite-dimensional models of convection. Phys. D 9(1–2) (1983), 52–64.10.1016/0167-2789(83)90291-9CrossRefGoogle Scholar
Mañé, R.. A proof of the ${C}^1$ stability conjecture. Publ. Math. Inst. Hautes Etudes Sci. 66 (1987), 161–210.10.1007/BF02698931CrossRefGoogle Scholar
Mischaikow, K. and Mrozek, M.. Chaos in the Lorenz equations: a computer assisted proof (I). Bull. Amer. Math. Soc. (N.S.) 32 (1995), 66–72.10.1090/S0273-0979-1995-00558-6CrossRefGoogle Scholar
Mischaikow, K. and Mrozek, M.. Chaos in the Lorenz equations: a computer assisted proof (II). Math. Comp. 67 (1998), 1023–1046.10.1090/S0025-5718-98-00945-4CrossRefGoogle Scholar
Mora, L. and Lizana, C.. Lower bounds for the Hausdorff dimension of the geometric Lorenz attractor the homoclinic case. Discrete Contin. Dyn. Syst. 22(3) (2008), 699–709.Google Scholar
Morales, C. A., Pacifico, M. J. and Pujals, E.. Robust transitive singular sets for 3-flows are partially hyperbolic attractors or repellers. Ann. of Math. (2) 160 (2004), 375–432.10.4007/annals.2004.160.375CrossRefGoogle Scholar
Morales, C. A., Pacifico, M. J. and San Martin, B.. Expanding Lorenz attractors through resonant double homoclinic loops. SIAM J. Math. Anal. 36(6) (2005), 1836–1861.10.1137/S0036141002415785CrossRefGoogle Scholar
Morales, C. A., Pacifico, M. J. and San Martin, B.. Contracting Lorenz attractors through resonant double homoclinic loops. SIAM J. Math. Anal. 38(1) (2006), 309–332.10.1137/S0036141004443907CrossRefGoogle Scholar
Moreira, C. G., Pacifico, M. J. and Romaña Ibarra, S.. Hausdorff dimension, Lagrange and Markov dynamical spectra for geometric Lorenz attractors. Bull. Amer. Math. Soc. (N.S.) 57 (2020), 269–292.10.1090/bull/1657CrossRefGoogle Scholar
Ovsyannikov, I. I. and Turaev, D.. Analytic proof of the existence of the Lorenz attractor in the extended Lorenz model. Nonlinearity 30 (2017), 115–137.10.1088/1361-6544/30/1/115CrossRefGoogle Scholar
Pacifico, M. J.. Structural stability of vector fields on 3-manifolds with boundary. J. Differential Equations 54(3) (1984), 346–372.10.1016/0022-0396(84)90148-7CrossRefGoogle Scholar
Pacifico, M. J. and Todd, M.. Thermodynamic formalism for contracting Lorenz flows. J. Stat. Phys. 139(1) (2010), 159–176.10.1007/s10955-010-9939-2CrossRefGoogle Scholar
Pacifico, M. J., Yang, F. and Yang, J.. Equilibrium states for the classical Lorenz attractor and sectional-hyperbolic attractors in higher dimensions. Preprint, 2023, arXiv:2209.10784.Google Scholar
Robinson, C.. Transitivity and invariant measures for the geometric model of the Lorenz equations. Ergod. Th. & Dynam. Sys. 4 (1984), 605–611.10.1017/S0143385700002674CrossRefGoogle Scholar
Robinson, C.. Homoclinic bifurcation to a transitive attractor of Lorenz type. Nonlinearity 2 (1989), 495–518.10.1088/0951-7715/2/4/001CrossRefGoogle Scholar
Robinson, C.. Homoclinic bifurcation to a transitive attractor of Lorenz type. II. SIAM J. Math. Anal. 23 (1992), 1255–1268.10.1137/0523070CrossRefGoogle Scholar
Robinson, C.. Nonsymmetric Lorenz attractors from a homoclinic bifurcation. SIAM J. Math. Anal. 32 (2000), 119–141.10.1137/S0036141098343598CrossRefGoogle Scholar
Rychlik, M. R.. Lorenz attractors through Shilnikov-type bifurcation. Ergod. Th. & Dynam. Sys. 10 (1990), 793–821.10.1017/S0143385700005915CrossRefGoogle Scholar
Shilnikov, L. P.. Bifurcation theory and quasihyperbolic attractors. Uspekhi Mat. Nauk 36 (1981), 240–241.Google Scholar
Sinai, Y.. Hyperbolic conditions for the Lorenz model. Phys. D 2 (1981), 3–7.10.1016/0167-2789(81)90053-1CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. (N.S.) 73 (1967), 747–817.10.1090/S0002-9904-1967-11798-1CrossRefGoogle Scholar
Smania, D. and Vidarte, J.. Existence of Ck-invariant foliations for Lorenz-type maps. J. Dynam. Differential Equations 30 (2018), 227–255.10.1007/s10884-016-9539-1CrossRefGoogle Scholar
Sparrow, C.. The Lorenz Equations: Bifurcations, Chaos and Strange Attractors. Springer, New York, NY, 1982.10.1007/978-1-4612-5767-7CrossRefGoogle Scholar
Steingenber, T.. Hausdorff dimension of attractor for two dimensional Lorenz transformations. Israel J. Math. 116 (2000), 253–269.10.1007/BF02773221CrossRefGoogle Scholar
Tucker, W.. The Lorenz attractor exists. C. R. Acad. Sci. Ser. I Math. 328 (1999), 1197–1202.Google Scholar
Tucker, W.. A rigorous ODE solver and Smale’s 14th problem. Found. Comput. Math. 2(1) (2002), 53–117.10.1007/s002080010018CrossRefGoogle Scholar
Viana, M.. What’s new on Lorenz strange attractors? Math. Intelligencer 22(3) (2000), 6–19.10.1007/BF03025276CrossRefGoogle Scholar
Viswanath, D.. The fractal property of the Lorenz attractor. Phys. D 190 (2004), 115–128.10.1016/j.physd.2003.10.006CrossRefGoogle Scholar
Williams, R.. One-dimensional nonwandering sets. Topology 6 (1967), 473–487.10.1016/0040-9383(67)90005-5CrossRefGoogle Scholar
Williams, R.. Expanding attractors. Publ. Math. Inst. Hautes Études Sci. 43 (1974), 169–203.10.1007/BF02684369CrossRefGoogle Scholar
Williams, R.. The structure of Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 73–99.10.1007/BF02684770CrossRefGoogle Scholar