Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-05-02T11:10:07.371Z Has data issue: false hasContentIssue false
  • English
  • Français

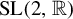Uniformity aspects of ${\mathrm {SL}}(2,{\mathbb R})$ cocycles and applications to Schrödinger operators defined over Boshernitzan subshifts

Part of: Ergodic theory Special classes of linear operators

Published online by Cambridge University Press:  20 November 2024

DAVID DAMANIK Open the ORCID record for DAVID DAMANIK [Opens in a new window]  and
DANIEL LENZ
DAVID DAMANIK
Affiliation:
Department of Mathematics, Rice University, Houston, TX 77005, USA (e-mail: [email protected])
DANIEL LENZ*
Affiliation:
Institute for Mathematics, Friedrich-Schiller University, Jena 07743, Germany
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider continuous 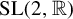${\mathrm {SL}}(2,{\mathbb R})$ valued cocycles over general dynamical systems and discuss a variety of uniformity notions. In particular, we provide a description of uniform one-parameter families of continuous 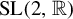${\mathrm {SL}}(2,{\mathbb R})$ cocycles as 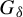$G_\delta $-sets. These results are then applied to Schrödinger operators with dynamically defined potentials. In the case where the base dynamics is given by a subshift satisfying the Boshernitzan condition, we show that for a generic continuous sampling function, the associated Schrödinger cocycles are uniform for all energies and, in the aperiodic case, the spectrum is a Cantor set of zero Lebesgue measure.

Keywords

uniform cocyclesSchrödinger operatorssubshiftszero-measure spectrum

MSC classification

Primary: 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 47B36: Jacobi (tridiagonal) operators (matrices) and generalizations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 23
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Dedicated to the memory of Michael Boshernitzan

References

Avila, A. and Bochi, J.. A uniform dichotomy for generic $\mathrm{SL}(2,\mathbb{R})$ cocycles over a minimal base. Bull. Soc. Math. France 135 (2007), 407–417.CrossRefGoogle Scholar
Avila, A., Bochi, J. and Damanik, D.. Cantor spectrum for Schrödinger operators with potentials arising from generalized skew-shifts. Duke Math. J. 146 (2009), 253–280.CrossRefGoogle Scholar
Avila, A., Bochi, J. and Damanik, D.. David opening gaps in the spectrum of strictly ergodic Schrödinger operators. J. Eur. Math. Soc. (JEMS) 14 (2012), 61–106.CrossRefGoogle Scholar
Avila, A. and Damanik, D.. Generic singular spectrum for ergodic Schrödinger operators. Duke Math. J. 130 (2005), 393–400.CrossRefGoogle Scholar
Avila, A., Damanik, D. and Zhang, Z.. Singular density of states measure for subshift and quasi-periodic Schrödinger operators. Comm. Math. Phys. 330 (2014), 469–498.CrossRefGoogle Scholar
Beckus, S. and Pogorzelski, F.. Spectrum of Lebesgue measure zero for Jacobi operators of quasicrystals. Math. Phys. Anal. Geom. 16 (2013), 289–308.CrossRefGoogle Scholar
Bellissard, J., Iochum, B., Scoppola, E. and Testard, D.. Spectral properties of one-dimensional quasicrystals. Comm. Math. Phys. 125 (1989), 527–543.CrossRefGoogle Scholar
Bochi, J. and Navas, A.. Almost reduction and perturbation of matrix cocycles. Ann. Inst. H. Poincaré C Anal. Non Linéaire 31 (2014), 1101–1107.CrossRefGoogle Scholar
Boshernitzan, M.. A condition for unique ergodicity of minimal symbolic flows. Ergod. Th. & Dynam. Sys. 12 (1992), 425–428.CrossRefGoogle Scholar
Boshernitzan, M. and Damanik, D.. Generic continuous spectrum for ergodic Schrödinger operators. Comm. Math. Phys. 283 (2008), 647–662.CrossRefGoogle Scholar
Boshernitzan, M. and Damanik, D.. The repetition property for sequences on tori generated by polynomials or skew-shifts. Israel J. Math. 174 (2009), 189–202.CrossRefGoogle Scholar
Bourgain, J.. Positivity and continuity of the Lyapounov exponent for shifts on $\mathbb{T}^d$ with arbitrary frequency vector and real analytic potential. J. Anal. Math. 96 (2005), 313–355.CrossRefGoogle Scholar
Bourgain, J. and Jitomirskaya, S.. Continuity of the Lyapunov exponent for quasiperiodic operators with analytic potential. J. Stat. Phys. 108 (2002), 1203–1218.CrossRefGoogle Scholar
Damanik, D.. Lyapunov exponents and spectral analysis of ergodic Schrödinger operators: a survey of Kotani theory and its applications. Spectral Theory and Mathematical Physics: A Festschrift in Honor of Barry Simon’s 60th Birthday (Proceedings of Symposia in Pure Mathematics, 76, Part 2). Ed. Gesztesy, F., Deift, P., Galvez, C., Perry, P. and Schlag, W.. American Mathematical Society, Providence, RI, 2007, pp. 539–563.CrossRefGoogle Scholar
Damanik, D.. Schrödinger operators with dynamically defined potentials. Ergod. Th. & Dynam. Sys. 37 (2017), 1681–1764.CrossRefGoogle Scholar
Damanik, D. and Fillman, J.. One-Dimensional Ergodic Schrödinger Operators, I. General Theory (Graduate Studies in Mathematics Series, 221). American Mathematical Society, Providence, RI, 2022.CrossRefGoogle Scholar
Damanik, D. and Fillman, J.. One-Dimensional Ergodic Schrödinger Operators, II. Special Classes, in preparation.Google Scholar
Damanik, D., Fillman, J. and Lukic, M.. Limit-periodic continuum Schrödinger operators with zero measure Cantor spectrum. J. Spectr. Theory 7 (2017), 1101–1118.CrossRefGoogle Scholar
Damanik, D., Fillman, J., Lukic, M. and Yessen, W.. Characterizations of uniform hyperbolicity and spectra of CMV matrices. Discrete Contin. Dyn. Syst. Ser. S 9 (2016), 1009–1023.Google Scholar
Damanik, D., Killip, R. and Simon, B.. Perturbations of orthogonal polynomials with periodic recursion coefficients. Ann. of Math. (2) 171 (2010), 1931–2010.CrossRefGoogle Scholar
Damanik, D. and Lenz, D.. A criterion of Boshernitzan and uniform convergence in the multiplicative ergodic theorem. Duke Math. J. 133 (2006), 95–123.CrossRefGoogle Scholar
Damanik, D. and Lenz, D.. Zero-measure Cantor spectrum for Schrödinger operators with low-complexity potentials. J. Math. Pures Appl. (9) 85 (2006), 671–686.CrossRefGoogle Scholar
Damanik, D. and Lenz, D.. Uniform Szegő cocycles over strictly ergodic subshifts. J. Approx. Theory 144 (2007), 133–138.CrossRefGoogle Scholar
Duarte, P. and Klein, S.. Continuity of the Lyapunov exponents for quasiperiodic cocycles. Comm. Math. Phys. 332 (2014), 1113–1166.CrossRefGoogle Scholar
Duarte, P. and Klein, S.. Lyapunov Exponents of Linear Cocycles: Continuity via Large Deviations (Atlantis Studies in Dynamical Systems, 3). Atlantis Press, Paris, 2016.CrossRefGoogle Scholar
Fabbri, R. and Johnson, R.. Genericity of exponential dichotomy for two-dimensional differential systems. Ann. Mat. Pura Appl. (4) 178 (2000), 175–193.CrossRefGoogle Scholar
Fang, L., Damanik, D. and Guo, S.. Generic spectral results for CMV matrices with dynamically defined Verblunsky coefficients. J. Funct. Anal. 279 (2020), 108803.CrossRefGoogle Scholar
Furman, A.. On the multiplicative ergodic theorem for uniquely ergodic ergodic systems. Ann. Inst. Henri Poincaré Probab. Statist. 33 (1997), 797–815.CrossRefGoogle Scholar
Goldstein, M. and Schlag, W.. Hölder continuity of the integrated density of states for quasiperiodic Schrödinger equations and averages of shifts of subharmonic functions. Ann. of Math. (2) 154 (2001), 155–203.CrossRefGoogle Scholar
Grigorchuk, R., Lenz, D., Nagnibeda, T. and Sell, D.. Subshifts with leading sequences, uniformity of cocycles and spectral theory of Schreier graphs . Adv. Math. 407 (2022), 108550.CrossRefGoogle Scholar
Ishii, K.. Localization of eigenstates and transport phenomena in the one dimensional disordered system. Supp. Theor. Phys. 53 (1973), 77–138.CrossRefGoogle Scholar
Johnson, R.. Exponential dichotomy, rotation number, and linear differential operators with bounded coefficients. J. Differential Equations 61 (1986), 54–78.CrossRefGoogle Scholar
Johnson, R., Obaya, R., Novo, S., Núñez, C. and Fabbri, R.. Nonautonomous Linear Hamiltonian Systems: Oscillation, Spectral Theory and Control (Developments in Mathematics, 36). Springer, Cham, 2016.CrossRefGoogle Scholar
Kotani, S.. Ljapunov indices determine absolutely continuous spectra of stationary random one-dimensional Schrödinger operators. Stochastic Analysis (Kakata/Kyoto, 1982). Ed. Itô, K.. North Holland, Amsterdam, 1984, pp. 225–247.Google Scholar
Kotani, S.. Jacobi matrices with random potentials taking finitely many values. Rev. Math. Phys. 1 (1989), 129–133.CrossRefGoogle Scholar
Kotani, S.. Generalized Floquet theory for stationary Schrödinger operators in one dimension. Chaos Solitons Fractals 8 (1997), 1817–1854.CrossRefGoogle Scholar
Lenz, D.. Singular continuous spectrum of Lebesgue measure zero for one-dimensional quasicrystals. Comm. Math. Phys. 227 (2002), 119–130.CrossRefGoogle Scholar
Lenz, D.. Existence of non-uniform cocycles on uniquely ergodic systems. Ann. Inst. Henri Poincaré Probab. Stat. 40 (2004), 197–206.CrossRefGoogle Scholar
Liu, Q.-H. and Qu, Y.-H.. Uniform convergence of Schrödinger cocycles over simple Toeplitz subshift. Ann. Henri Poincaré 12 (2011), 153–172.CrossRefGoogle Scholar
Pastur, L.. Spectral properties of disordered systems in the one-body approximation. Comm. Math. Phys. 75 (1980), 179–196.CrossRefGoogle Scholar
Schlag, W.. Regularity and convergence rates for the Lyapunov exponents of linear cocycles. J. Mod. Dyn. 7 (2013), 619–637.CrossRefGoogle Scholar
Schreiber, S.. On growth rates of subadditive functions for semiflows. J. Differential Equations 148 (1998), 334–350.CrossRefGoogle Scholar
Sell, D.. Simple Toeplitz subshifts: combinatorial properties and uniformity of cocycles. PhD Thesis, Friedrich-Schiller Universität Jena, Jena, 2019.Google Scholar
Sturman, R. and Stark, J.. Semi-uniform ergodic theorems and applications to forced systems. Nonlinearity 13 (2000), 113–143.CrossRefGoogle Scholar
Sütő, A.. Singular continuous spectrum on a Cantor set of zero Lebesgue measure for the Fibonacci Hamiltonian. J. Stat. Phys. 56 (1989), 525–531.CrossRefGoogle Scholar
Viana, M.. Lectures on Lyapunov Exponents (Cambridge Studies in Advanced Mathematics, 145). Cambridge University Press, Cambridge, 2014.CrossRefGoogle Scholar
Walters, P.. Unique ergodicity and random matrix products. Lyapunov Exponents (Bremen, 1984) (Lecture Notes in Mathematics, 1186). Ed. Arnold, L. and Wihstutz, V.. Springer, Berlin 1986, pp. 37–55.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Reprint, Springer, New York, 2000.Google Scholar
Yoccoz, J.-C.. Some questions and remarks about $\mathrm{SL}(2,\mathbb{R})$ cocycles. Modern Dynamical Systems and Applications. Ed. Brin, M., Hasselblatt, B. and Pesin, Y.. Cambridge University Press, Cambridge, 2004, pp. 447–458.Google Scholar
Zhang, Z.. Uniform hyperbolicity and its relation with spectral analysis of 1D discrete Schrödinger operators. J. Spectr. Theory 10 (2020), 1471–1517.CrossRefGoogle Scholar