We prove 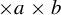$\times a \times b$ measure rigidity for multiplicatively independent pairs when 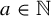$a\in \mathbb {N}$ and 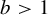$b>1$ is a ‘specified’ real number (the b-expansion of 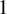$1$ has a tail or bounded runs of 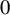$0$s) under a positive entropy condition. This is done by proving a mean decay of the Fourier series of the point masses average along 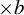$\times b$ orbits. We also prove a quantitative version of this decay under stronger conditions on the 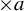$\times a$ invariant measure. The quantitative version together with the 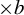$\times b$ invariance of the limit measure is a step toward a general Host-type pointwise equidistribution theorem in which the equidistribution is for Parry measure instead of Lebesgue. We show that finite memory length measures on the a-shift meet the mentioned conditions for mean convergence. Our main proof relies on techniques of Hochman.