Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-29T11:02:48.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Shub’s example revisited

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  23 September 2024

CHAO LIANG ,
RADU SAGHIN ,
FAN YANG  and
JIAGANG YANG
CHAO LIANG
Affiliation:
School of Statistics and Mathematics, Central University of Finance and Economics, Beijing 100081, China (e-mail: [email protected])
RADU SAGHIN*
Affiliation:
Instituto de Matemática, Pontificia Universidad Católica de Valparaíso, Blanco Viel 596, Cerro Barón, Valparaíso, Chile
FAN YANG
Affiliation:
Department of Mathematics, Wake Forest University, Winston-Salem, NC, USA (e-mail: [email protected])
JIAGANG YANG
Affiliation:
Departamento de Geometria, Instituto de Matemática e Estatística, Universidade Federal Fluminense, Niterói, Brazil (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a class of robustly transitive diffeomorphisms on 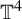${\mathbb T}^4$ introduced by Shub [Topologically transitive diffeomorphisms of 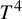$T^4$. Proceedings of the Symposium on Differential Equations and Dynamical Systems (Lecture notes in Mathematics, 206). Ed. D. Chillingworth. Springer, Berlin, 1971, pp. 39–40], satisfying an additional bunching condition, we show that there exists a 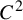$C^2$ open and 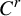$C^r$ dense subset 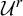${\mathcal U}^r$, 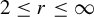$2\leq r\leq \infty $, such that any two hyperbolic points of 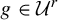$g\in {\mathcal U}^r$ with stable index 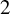$2$ are homoclinically related. As a consequence, every $g\in {\mathcal U}^r$ admits a unique homoclinic class associated to the hyperbolic periodic points with index 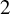$2$, and this homoclinic class coincides with the whole ambient manifold. Moreover, every 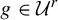$g\in {\mathcal U}^r$ admits at most one measure of maximal entropy, and every 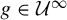$g\in {\mathcal U}^{\infty }$ admits a unique measure of maximal entropy.

Keywords

partially hyperbolic diffeomorphismshomoclinic classesequilibrium states

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings 37C40: Smooth ergodic theory, invariant measures
Secondary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37C29: Homoclinic and heteroclinic orbits
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 45 , Issue 3 , March 2025 , pp. 894 - 914
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Álvarez, C. F.. Hyperbolicity of maximal entropy measures for certain maps isotopic to Anosov diffeomorphisms. J. Math. Anal. Appl. 528(1) (2023), Paper no. 127531.CrossRefGoogle Scholar
Ben Ovadia, S.. Symbolic dynamics for non-uniformly hyperbolic diffeomorphisms of compact smooth manifolds. J. Mod. Dyn. 13 (2018), 43–113.CrossRefGoogle Scholar
Ben Ovadia, S.. The set of points with Markovian symbolic dynamics for non-uniformly hyperbolic diffeomorphisms. Ergod. Th. & Dynam. Sys. 41(11) (2021), 3244–3269.CrossRefGoogle Scholar
Bowen, R.. Entropy-expansive maps. Trans. Amer. Math. Soc. 164 (1972), 323–331.CrossRefGoogle Scholar
Brown, A.. Smoothness of stable holonomies inside center-stable manifolds. Ergod. Th. & Dynam. Sys. 42(12) (2022), 3593–3618.CrossRefGoogle Scholar
Buzzi, J.. Intrinsic ergodicity of smooth interval maps. Israel J. Math. 100 (1997), 125–161.CrossRefGoogle Scholar
Buzzi, J., Crovisier, S. and Sarig, O.. Measures of maximal entropy for surface diffeomorphisms. Ann. of Math. (2) 195(2) (2022), 421–508.CrossRefGoogle Scholar
Carvalho, M. and Pérez, S. A.. Periodic points and measures for a class of skew-products. Israel J. Math. 245(1) (2021), 455–500.CrossRefGoogle Scholar
Climenhaga, V. and Thompson, D. J.. Unique equilibrium states for flows and homeomorphisms with non-uniform structure. Adv. Math. 303 (2016), 745–799.CrossRefGoogle Scholar
Crovisier, S., Obata, D. and Poletti, M.. Uniqueness of $u$ -gibbs measures for hyperbolic skew products on ${T}^4$ . 2023.CrossRefGoogle Scholar
Fisher, T., Potrie, R. and Sambarino, M.. Dynamical coherence of partially hyperbolic diffeomorphisms of tori isotopic to Anosov. Math. Z. 278(1–2) (2014), 149–168.CrossRefGoogle Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Proc. Sympos. Pure Math., Vol. XIV, Berkeley, CA, 1968). Ed. S.-s. Chern and S. Smale. American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Ledrappier, F. and Strelcyn, J.-M.. A proof of the estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2(2) (1983), 203–219; 1982.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16(3) (1977), 568–576.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension. Ann. of Math. (2) 122(3) (1985), 540–574.CrossRefGoogle Scholar
Liao, G., Viana, M. and Yang, J.. The entropy conjecture for diffeomorphisms away from tangencies. J. Eur. Math. Soc. (JEMS) 15(6) (2013), 2043–2060.CrossRefGoogle Scholar
Mañé, R.. Contributions to the stability conjecture. Topology 17(4) (1978), 383–396.CrossRefGoogle Scholar
Manning, A.. There are no new Anosov diffeomorphisms on tori. Amer. J. Math. 96 (1974), 422–429.CrossRefGoogle Scholar
Newhouse, S. E. and Young, L.-S.. Dynamics of certain skew products. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007). Ed. J. Palis Jr. Springer, Berlin, 1983, pp. 611–629.CrossRefGoogle Scholar
Obata, D.. Open sets of partially hyperbolic skew products having a unique SRB measure. Adv. Math. 427 (2023), Paper no. 109136.CrossRefGoogle Scholar
Pacifico, M. J., Yang, F. and Yang, J.. Existence and uniqueness of equilibrium states for systems with specification at a fixed scale: an improved Climenhaga–Thompson criterion. Nonlinearity 35(12) (2022), 5963–5992.CrossRefGoogle Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Partial differentiability of invariant splittings. J. Stat. Phys. 114(3–4) (2004), 891–921.CrossRefGoogle Scholar
Pujals, E. R. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. (2) 151(3) (2000), 961–1023.CrossRefGoogle Scholar
Shub, M.. Topologically transitive diffeomorphisms of ${T}^4$ . Proceedings of the Symposium on Differential Equations and Dynamical Systems (Lecture Notes in Mathematics, 206). Ed. Chillingworth, D.. Springer, Berlin, 1971, pp. 39–40.CrossRefGoogle Scholar
Smale, S.. Diffeomorphisms with many periodic points. Differential and Combinatorial Topology (A Symposium in Honor of Marston Morse). Princeton University Press, Princeton, NJ, 1965, pp. 63–80.CrossRefGoogle Scholar
Tahzibi, A. and Yang, J.. Invariance principle and rigidity of high entropy measures. Trans. Amer. Math. Soc. 371(2) (2019), 1231–1251.CrossRefGoogle Scholar
Wen, L.. Homoclinic tangencies and dominated splittings. Nonlinearity 15(5) (2002), 1445–1469.CrossRefGoogle Scholar
Yang, J.. Entropy along expanding foliations. Adv. Math. 389 (2021), Paper no. 107893.CrossRefGoogle Scholar
Yomdin, Y.. Volume growth and entropy. Israel J. Math. 57(3) (1987), 285–300.CrossRefGoogle Scholar