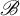Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-29T15:08:32.095Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant measures for $\mathscr {B}$-free systems revisited

Part of: Set functions and measures on spaces with additional structure Topological dynamics Ergodic theory

Published online by Cambridge University Press:  08 March 2024

AURELIA DYMEK Open the ORCID record for AURELIA DYMEK [Opens in a new window] ,
JOANNA KUŁAGA-PRZYMUS Open the ORCID record for JOANNA KUŁAGA-PRZYMUS [Opens in a new window]  and
DANIEL SELL Open the ORCID record for DANIEL SELL [Opens in a new window]
AURELIA DYMEK*
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland (e-mail: [email protected], [email protected])
JOANNA KUŁAGA-PRZYMUS
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland (e-mail: [email protected], [email protected])
DANIEL SELL
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland (e-mail: [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 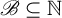$\mathscr {B} \subseteq \mathbb {N} $, the 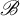$ \mathscr {B} $-free subshift 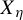$ X_{\eta } $ is the orbit closure of the characteristic function of the set of 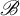$ \mathscr {B} $-free integers. We show that many results about invariant measures and entropy, previously only known for the hereditary closure of 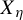$ X_{\eta } $, have their analogues for 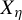$ X_{\eta } $ as well. In particular, we settle in the affirmative a conjecture of Keller about a description of such measures [G. Keller. Generalized heredity in $\mathcal B$-free systems. Stoch. Dyn. 21(3) (2021), Paper No. 2140008]. A central assumption in our work is that 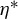$\eta ^{*} $ (the Toeplitz sequence that generates the unique minimal component of 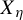$ X_{\eta } $) is regular. From this, we obtain natural periodic approximations that we frequently use in our proofs to bound the elements in 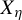$ X_{\eta } $ from above and below.

Keywords

invariant measuresB-free dynamicsdynamical diagramstopological entropyintrinsic ergodicityentropy densitytautness

MSC classification

Primary: 28C10: Set functions and measures on topological groups or semigroups, Haar measures, invariant measures 37A05: Measure-preserving transformations
Secondary: 37B40: Topological entropy 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 10 , October 2024 , pp. 2901 - 2932
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baake, M. and Grimm, U.. Aperiodic Order. Volume 1: A Mathematical Invitation (Encyclopedia of Mathematics and its Applications, 149). Cambridge University Press, Cambridge, 2013; with a foreword by R. Penrose.10.1017/CBO9781139025256CrossRefGoogle Scholar
Bergelson, V., Downarowicz, T. and Vandehey, J.. Deterministic functions on amenable semigroups and a generalization of the Kamae–Weiss theorem on normality preservation. J. Anal. Math. 148(1) (2022), 213–286.10.1007/s11854-022-0226-3CrossRefGoogle Scholar
Davenport, H. and Erdös, P.. On sequences of positive integers. J. Indian Math. Soc. (N.S.) 15 (1951), 19–24.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385). Ed. Kolyada, S., Manin, Y. and Ward, T.. American Mathematical Society, Providence, RI, 2005, pp. 7–37.10.1090/conm/385/07188CrossRefGoogle Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18). Cambridge University Press, Cambridge, 2011.Google Scholar
Dymek, A., Kasjan, S. and Kułaga-Przymus, J.. Minimality of $\mathfrak{B}$ -free systems in number fields. Discrete Contin. Dyn. Syst. 43(9) (2023), 3512–3548.10.3934/dcds.2023056CrossRefGoogle Scholar
Dymek, A., Kasjan, S., Kułaga-Przymus, J. and Lemańczyk, M.. 𝔅-free sets and dynamics. Trans. Amer. Math. Soc. 370(8) (2018), 5425–5489.Google Scholar
Eizenberg, A., Kifer, Y. and Weiss, B. Large deviations for Zd-actions. Comm. Math. Phys. 164(3) (1994), 433–454.Google Scholar
El Abdalaoui, E. H., Lemańczyk, M. and de la Rue, T.. A dynamical point of view on the set of 𝔅-free integers. Int. Math. Res. Not. IMRN 16 (2015), 7258–7286.10.1093/imrn/rnu164CrossRefGoogle Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.10.1090/surv/101CrossRefGoogle Scholar
Hall, R. R.. Sets of Multiples (Cambridge Tracts in Mathematics, 118). Cambridge University Press, Cambridge, 1996.10.1017/CBO9780511566011CrossRefGoogle Scholar
Jacobs, K. and Keane, M.. $0-1$ -sequences of Toeplitz type. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 13 (1969), 123–131.Google Scholar
Kasjan, S., Keller, G. and Lemańczyk, M.. Dynamics of 𝔅-free sets: a view through the window. Int. Math. Res. Not. IMRN 9 (2019), 2690–2734.Google Scholar
Kechris, A. S.. Classical Descriptive Set Theory (Graduate Texts in Mathematics, 156). Springer-Verlag, New York, 1995.10.1007/978-1-4612-4190-4CrossRefGoogle Scholar
Keller, G.. Tautness for sets of multiples and applications to 𝔅-free dynamics. Studia Math. 247(2) (2019), 205–216.Google Scholar
Keller, G.. Generalized heredity in 𝔅-free systems. Stoch. Dyn. 21(3) (2021), Paper no. 2140008.10.1142/S0219493721400086CrossRefGoogle Scholar
Keller, G.. Irregular 𝔅-free Toeplitz sequences via Besicovitch’s construction of sets of multiples without density. Monatsh. Math. 199(4) (2022), 801–816.Google Scholar
Keller, G. and Richard, C.. Dynamics on the graph of the torus parametrization. Ergod. Th. & Dynam. Sys. 38(3) (2018), 1048–1085.10.1017/etds.2016.53CrossRefGoogle Scholar
Konieczny, J., Kupsa, M. and Kwietniak, D.. Arcwise connectedness of the set of ergodic measures of hereditary shifts. Proc. Amer. Math. Soc. 146(8) (2018), 3425–3438.10.1090/proc/14029CrossRefGoogle Scholar
Konieczny, J., Kupsa, M. and Kwietniak, D.. On $\overline{d}$ -approachability, entropy density and 𝔅-free shifts. Ergod. Th. & Dynam. Sys. 43(3) (2023), 943–970.Google Scholar
Kułaga-Przymus, J., Lemańczyk, M. and Weiss, B.. On invariant measures for 𝔅-free systems. Proc. Lond. Math. Soc. (3) 110(6) (2015), 1435–1474.Google Scholar
Kułaga-Przymus, J., Lemańczyk, M. and Weiss, B.. Hereditary subshifts whose simplex of invariant measures is Poulsen. Ergodic Theory, Dynamical Systems, and the Continuing Influence of John C. Oxtoby (Contemporary Mathematics, 678). Ed. Auslander, J., Johnson, A. and Silva, C. E.. American Mathematical Society, Providence, RI, 2016, pp. 245–253.10.1090/conm/678/13651CrossRefGoogle Scholar
Kułaga-Przymus, J. and Lemańczyk, M. D. Hereditary subshifts whose measure of maximal entropy does not have the Gibbs property. Colloq. Math. 166(1) (2021), 107–127.10.4064/cm8223-11-2020CrossRefGoogle Scholar
Kułaga-Przymus, J., Lemańczyk, M. D. and Rams, M.. Basic thermodynamical formalism for sandwich subshifts. Preprint, 2024, https://arxiv.org/pdf/2402.12579.pdf.Google Scholar
Kwietniak, D.. Topological entropy and distributional chaos in hereditary shifts with applications to spacing shifts and beta shifts. Discrete Contin. Dyn. Syst. 33(6) (2013), 2451–2467.10.3934/dcds.2013.33.2451CrossRefGoogle Scholar
Kwietniak, D., Łącka, M. and Oprocha, P.. Generic points for dynamical systems with average shadowing. Monatsh. Math. 183(4) (2017), 625–648.10.1007/s00605-016-1002-1CrossRefGoogle Scholar
Lemańczyk, M. D.. Recurrence of stochastic processes in some concentration of measure and entropy problems. Available at: https://www.mimuw.edu.pl/sites/default/files/lemanczyk_rozprawa_doktorska.pdf.Google Scholar
Lindenstrauss, J., Olsen, G. and Sternfeld, Y.. The Poulsen simplex. Ann. Inst. Fourier (Grenoble) 28(1) (1978), vi, 91–114.10.5802/aif.682CrossRefGoogle Scholar
Mirsky, L.. Note on an asymptotic formula connected with $r$ -free integers. Q. J. Math. Oxford Ser. 18 (1947), 178–182.10.1093/qmath/os-18.1.178CrossRefGoogle Scholar
Mirsky, L.. Arithmetical pattern problems relating to divisibility by $r$ th powers. Proc. Lond. Math. Soc. (2) 50 (1949), 497–508.Google Scholar
Peckner, R.. Uniqueness of the measure of maximal entropy for the squarefree flow. Israel J. Math. 210(1) (2015), 335–357.10.1007/s11856-015-1255-8CrossRefGoogle Scholar
Pfister, C.-E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Applications to the β-shifts. Nonlinearity 18(1) (2005), 237–261.Google Scholar
Sarnak, P.. Three lectures on the Möbius function, randomness and dynamics. Available at: http://publications.ias.edu/sarnak/.Google Scholar
Williams, S.. Toeplitz minimal flows which are not uniquely ergodic. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 67(1) (1984), 95–107.Google Scholar