Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-29T13:41:14.323Z Has data issue: false hasContentIssue false
  • English
  • Français

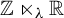Global rigidity of smooth ${\mathbb{Z}}\ltimes _{\unicode{x3bb}}{\mathbb{R}}$-actions on ${\mathbb{T}}^{2}$

Part of: Smooth dynamical systems: general theory

Published online by Cambridge University Press:  14 October 2024

CHANGGUANG DONG  and
YI SHI
CHANGGUANG DONG*
Affiliation:
Chern Institute of Mathematics and LPMC, Nankai University, Tianjin 300071, Tianjin, China
YI SHI
Affiliation:
School of Mathematics, Sichuan University, Chengdu 610065, Sichuan, China (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 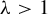$\unicode{x3bb}>1$, we consider the locally free 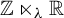${\mathbb Z}\ltimes _\unicode{x3bb} \mathbb R$ actions on 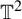$\mathbb T^2$. We show that if the action is $C^r$ with 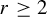$r\geq 2$, then it is 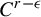$C^{r-\epsilon }$-conjugate to an affine action generated by a hyperbolic automorphism and a linear translation flow along the expanding eigen-direction of the automorphism. In contrast, there exists a 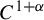$C^{1+\alpha }$-action which is semi-conjugate, but not topologically conjugate to an affine action.

Keywords

global rigiditysolvable group actionAnosov diffeomorphismsmooth conjugacy

MSC classification

Primary: 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations
Secondary: 37C15: Topological and differentiable equivalence, conjugacy, invariants, moduli, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 45 , Issue 4 , April 2025 , pp. 1161 - 1176
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Asaoka, M.. Local rigidity of homogeneous actions of parabolic subgroups of rank-one Lie groups. J. Mod. Dyn. 9 (2015), 191–201.CrossRefGoogle Scholar
Asaoka, M.. Local rigidity problem of smooth group actions. Sugaku Expositions 30(2) (2017), 207–233.CrossRefGoogle Scholar
Benoist, Y., Foulon, P. and Labourie, F.. Flots d’Anosov à distributions de Liapounov différentiables, I. Hyperbolic behaviour of dynamical systems (Paris, 1990). Ann. Inst. H. Poincaré Phys. Théor. 53(4) (1990), 395–412.Google Scholar
Benoist, Y., Foulon, P. and Labourie, F.. Flots d’Anosov à distributions stable et instable différentiables. J. Amer. Math. Soc. 5(1) (1992), 33–74.Google Scholar
Benoist, Y. and Labourie, F.. Sur les difféomorphismes d’Anosov affines à feuilletages stable et instable différentiables. Invent. Math. 111(2) (1993), 285–308.CrossRefGoogle Scholar
Berend, D.. Multi-invariant sets on tori. Trans. Amer. Math. Soc. 280(2) (1983), 509–532.CrossRefGoogle Scholar
Bonatti, C., Monteverde, I., Navas, A. and Rivas, C.. Rigidity for ${C}^1$ actions on the interval arising from hyperbolicity I: solvable groups. Math. Z. 286(3–4) (2017), 919–949.CrossRefGoogle Scholar
Burslem, L. and Wilkinson, A.. Global rigidity of solvable group actions on ${S}^1$ . Geom. Topol. 8(2) (2004), 877–924.CrossRefGoogle Scholar
Crovisier, S. and Potrie, R.. Introduction to Partially Hyperbolic Dynamics. School on Dynamical Systems, ICTP, Trieste, 2015.Google Scholar
Damjanović, D. and Katok, A.. Local rigidity of partially hyperbolic actions I. KAM method and ${\mathbb{Z}}^k$ actions on the torus. Ann. of Math. (2) 172(3) (2010), 1805–1858.CrossRefGoogle Scholar
Damjanović, D. and Katok, A.. Local rigidity of partially hyperbolic actions. II. The geometric method and restrictions of Weyl chamber flows on $SL(n,\mathbb{R})/\varGamma$ . Int. Math. Res. Not. IMRN 2011(19) 2011, 4405–4430.Google Scholar
Damjanović, D., Spatzier, R., Vinhage, K. and Xu, D.. Anosov actions: classification and the Zimmer program. Preprint, 2023, arXiv:2211.08195.Google Scholar
de la Llave, R.. Invariants for smooth conjugacy of hyperbolic dynamical systems II. Comm. Math. Phys. 109 (1987), 368–378.CrossRefGoogle Scholar
de la Llave, R.. Smooth conjugacy and SRB measures for uniformly and non-uniformly hyperbolic systems. Comm. Math. Phys. 150 (1992), 289–320.CrossRefGoogle Scholar
DeWitt, J. and Gogolev, A.. Dominated splitting from constant periodic data and global rigidity of Anosov automorphisms. Geom. Funct. Anal. 34(5) (2024), 1370–1398.CrossRefGoogle Scholar
Einsiedler, M., Katok, A. and Lindenstrauss, E.. Invariant measures and the set of exceptions to Littlewood’s conjecture. Ann. of Math. (2), 164(2) (2006), 513–560.CrossRefGoogle Scholar
Einsiedler, M. and Lindenstrauss, E.. On measures invariant under tori on quotients of semisimple groups. Ann. of Math. (2) 181(3) (2015), 993–1031.CrossRefGoogle Scholar
Fisher, D.. Local rigidity of group actions: past, present, future. Dynamics, Ergodic Theory, and Geometry (Mathematical Sciences Research Institute Publications, 54). Ed. Fisher, D.. Cambridge University Press, Cambridge, 2007, pp. 45–97.CrossRefGoogle Scholar
Flaminio, L. and Katok, A.. Rigidity of symplectic Anosov diffeomorphisms on low-dimensional tori. Ergod. Th. & Dynam. Sys. 11(3) (1991), 427–441.CrossRefGoogle Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV–XVI). American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.CrossRefGoogle Scholar
Ghys, E.. Rigidité différentiable des groupes fuchsiens. Publ. Math. Inst. Hautes Études Sci. 78 (1993), 163–185.CrossRefGoogle Scholar
Giulietti, P. and Liverani, C.. Parabolic dynamics and anisotropic Banach spaces. J. Eur. Math. Soc. (JEMS) 21(9) (2019), 2793–2858.CrossRefGoogle Scholar
Gogolev, A.. Bootstrap for local rigidity of Anosov automorphisms of the 3-torus. Comm. Math. Phys. 352(2) (2017), 439–455.CrossRefGoogle Scholar
Gogolev, A. and Shi, Y.. Joint integrability and spectral rigidity for Anosov diffeomorphisms. Proc. Lond. Math. Soc. (3) 127(6) (2023), 1693–1748.CrossRefGoogle Scholar
Gu, R.. Smooth stable foliations of Anosov diffeomorphisms. Preprint, 2023, arXiv:2310.19088, C. R. Math., accepted.Google Scholar
Hector, G. and Hirsch, U.. Introduction to the Geometry of Foliations. Part A. Foliations on Compact Surfaces, Fundamentals for Arbitrary Codimension, and Holonomy, 2nd edn. Friedr. Vieweg & Sohn, Braunschweig, 1986.Google Scholar
Herman, M. R.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49(1) (1979), 5–233.CrossRefGoogle Scholar
Hurtado, S. and Xue, J.. Global rigidity of some abelian-by-cyclic group actions on ${T}^2$ . Geom. Topol. 25(6) (2021), 3133–3178.CrossRefGoogle Scholar
Journé, J.-L., A regularity lemma for functions of several variables. Rev. Mat. Iberoam. 4(2) (1988), 187–193.CrossRefGoogle Scholar
Kalinin, B.. Liv $\check{s}$ ic theorem for matrix cocycles. Ann. of Math. (2) 173(2) (2011), 1025–1042.CrossRefGoogle Scholar
Kalinin, B., Katok, A. and Rodriguez Hertz, F.. Nonuniform measure rigidity. Ann. of Math. (2) 174(1) (2011), 361–400.CrossRefGoogle Scholar
Katznelson, Y. and Ornstein, D.. The differentiability of the conjugation of certain diffeomorphisms of the circle. Ergod. Th. & Dynam. Sys. 9(4) (1989), 643–680.CrossRefGoogle Scholar
Khanin, K. and Teplinsky, A.. Herman’s theory revisited. Invent. Math. 178(2) (2009), 333–344.CrossRefGoogle Scholar
Liu, Q.. Local rigidity of certain solvable group actions on tori. Discrete Contin. Dyn. Syst. 41(2) (2021), 553–567.CrossRefGoogle Scholar
Pinto, A. A. and Rand, D. A.. Rigidity of hyperbolic sets on surfaces. J. Lond. Math. Soc. (2) 71(2) (2005), 481–502.CrossRefGoogle Scholar
Potrie, R.. Partial hyperbolicity and attracting regions in 3-dimensional manifolds. Preprint, 2012, arXiv:1207.1822; Doctoral Thesis, Universidad de la Republica, Montevideo, Uruguay and Université Sorbonne Paris Nord, 2012.Google Scholar
Ratner, M.. Invariant measures and orbit closures for unipotent actions on homogeneous spaces. Geom. Funct. Anal. 4(2) (1994), 236–257.CrossRefGoogle Scholar
Robinson, C.. Dynamical Systems. Stability, Symbolic Dynamics, and Chaos (Studies in Advanced Mathematics). CRC Press, Boca Raton, FL, 1999.Google Scholar
Sigmund, K.. Generic properties of invariant measures for Axiom A diffeomorphisms. Invent. Math. 11 (1970), 99–109.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. (N.S.) 73 (1967), 747–817.CrossRefGoogle Scholar
Spatzier, R. and Vinhage, K.. Cartan actions of higher rank abelian groups and their classification. J. Amer. Math. Soc. 37(3) (2024), 731–859.CrossRefGoogle Scholar
Wang, Z. J.. Local rigidity of higher rank non-abelian action on torus. Ergod. Th. & Dynam. Sys. 39(6) (2019), 1668–1709.CrossRefGoogle Scholar
Wilkinson, A. and Xue, J.. Rigidity of some abelian-by-cyclic solvable group actions on ${T}^n$ . Comm. Math. Phys. 376 (2020) 1223–1259.CrossRefGoogle Scholar