No CrossRef data available.
Published online by Cambridge University Press: 18 February 2020
We study the continuity of topological entropy of general diffeomorphisms on line. First, we prove that the entropy map is continuous with respect to the strong 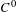 $C^{0}$-topology on the union of uniformly topologically hyperbolic diffeomorphisms contained in
$C^{0}$-topology on the union of uniformly topologically hyperbolic diffeomorphisms contained in 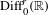 $\text{Diff}_{0}^{r}(\mathbb{R})$ (whose first derivative is uniformly away from zero), which is a
$\text{Diff}_{0}^{r}(\mathbb{R})$ (whose first derivative is uniformly away from zero), which is a 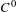 $C^{0}$-open and
$C^{0}$-open and 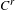 $C^{r}$-dense subset of
$C^{r}$-dense subset of 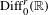 $\text{Diff}_{0}^{r}(\mathbb{R})$,
$\text{Diff}_{0}^{r}(\mathbb{R})$, 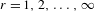 $r=1,2,\ldots ,\infty$, and
$r=1,2,\ldots ,\infty$, and  $\unicode[STIX]{x1D714}$ (real analytic). Second, we give some examples where entropy map is not continuous. Finally, we prove some results on the continuity of entropy of general diffeomorphisms on the (real) line.
$\unicode[STIX]{x1D714}$ (real analytic). Second, we give some examples where entropy map is not continuous. Finally, we prove some results on the continuity of entropy of general diffeomorphisms on the (real) line.