Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-29T08:30:35.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of Newton maps

Part of: Complex dynamical systems

Published online by Cambridge University Press:  15 February 2022

XIAOGUANG WANG ,
YONGCHENG YIN  and
JINSONG ZENG
XIAOGUANG WANG
Affiliation:
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, P. R. China (e-mail: [email protected], [email protected])
YONGCHENG YIN
Affiliation:
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, P. R. China (e-mail: [email protected], [email protected])
JINSONG ZENG*
Affiliation:
School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, P. R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

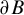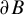In this paper, we study the dynamics of the Newton maps for arbitrary polynomials. Let p be an arbitrary polynomial with at least three distinct roots, and f be its Newton map. It is shown that the boundary $\partial B$ of any immediate root basin B of f is locally connected. Moreover, $\partial B$ is a Jordan curve if and only if 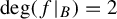$\mathrm {deg}(f|_B)=2$ . This implies that the boundaries of all components of root basins, for the Newton maps for all polynomials, from the viewpoint of topology, are tame.

Keywords

Newton mapspuzzleslocal connectivity

MSC classification

Primary: 37F45: Holomorphic families of dynamical systems; the Mandelbrot set; bifurcations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 3 , March 2023 , pp. 1035 - 1080
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alexander, D.. A History of Complex Dynamics: From Schroder to Fatou and Julia (Aspects of Mathematics, Vol. E no. 24). Vieweg Teubner Verlag, Braunschweig, 1994.CrossRefGoogle Scholar
Aspenberg, M. and Roesch, P.. Newton maps as matings of cubic polynomials. Proc. Lond. Math. Soc. (3) 113(1) (2016), 77–112.CrossRefGoogle Scholar
Barański, K.. From Newton’s method to exotic basins Part I: the parameter space. Fund. Math. 158 (1998), 249–288.CrossRefGoogle Scholar
Bergweiler, W.. Newton’s method and a class of meromorphic functions without wandering domains. Ergod. Th. & Dynam. Sys. 13 (1993) 231–247.CrossRefGoogle Scholar
Baranski, K., Fagella, N., Jarque, X. and Karpinska, B.. On the connectivity of the Julia sets of meromorphic functions. Invent. Math. 198(3) (2014), 591–636.CrossRefGoogle Scholar
Baranski, K., Fagella, N., Jarque, X. and Karpinska, B.. Connectivity of Julia sets of Newton maps: a unified approach. Rev. Mat. Iberoam. 34(3) (2018), 1211–1228.CrossRefGoogle Scholar
Cayley, A.. Desiderata and suggestions: no. 3. The Newton–Fourier imaginary problem. Amer. J. Math. 2(1) (1879), 97.CrossRefGoogle Scholar
Cui, G., Gao, Y. and Zeng, J.. Invariant graphs of rational maps. Preprint, 2019, arXiv:1907.02870.Google Scholar
Denjoy, A.. Sur l’itération des fonctions analytiques. C. R. Math. Acad. Sci. Paris 182 (1926), 255–257.Google Scholar
Drach, K., Mikulich, Y., Rückert, J. and Schleicher, D.. A combinatorial classification of postcritically fixed Newton maps. Ergod. Th. & Dynam. Sys. 39(11) (2019), 2983–3014.CrossRefGoogle Scholar
Head, J.. The combinatorics of Newtons method for cubic polynomials. Thesis, Cornell University, 1987.Google Scholar
Hubbard, J., Schleicher, D. and Sutherland, S.. How to find all roots of complex polynomials by Newton’s method. Invent. Math. 146 (2001), 1–33.CrossRefGoogle Scholar
Kahn, J. and Lyubich, M.. Local connectivity of Julia sets for unicritical polynomials. Ann. of Math. (2) 170 (2009), 413–426.CrossRefGoogle Scholar
Kahn, J. and Lyubich, M.. The Quasi–Additivity law in conformal geometry. Ann. of Math. (2) 169 (2009), 561–593.CrossRefGoogle Scholar
Kozlovski, O. and van Strien, S.. Local connectivity and quasi-conformal rigidity of non-renormalizable polynomials. Proc. Lond. Math. Soc. (2) 99 (2009), 275–296.CrossRefGoogle Scholar
Kozlovski, O., Shen, W. and van Strien, S.. Rigidity for real polynomials. Ann. of Math. (2) 165 (2007), 749–841.CrossRefGoogle Scholar
Lyubich, M. and Minsky, Y.. Laminations in holomorphic dynamics. J. Differential Geom. 47 (1997), 17–94.CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Mikulich, Y., Rückert, J. and Schleicher, D.. A combinatorial classification of post-critically fixed Newton maps. Preprint, 2018, arXiv:1510.02771v1.Google Scholar
Przytycki, F.. Remarks on the simple connectedness of basins of sinks for iterations of rational maps. Collection: Dynamical Systems and Ergodic Theory (Warsaw, 1986). Vol. 23. Banach Center Publications, Warsaw, 1989, pp. 229–235.Google Scholar
Qiu, W. and Yin, Y.. Proof of the Branner–Hubbard conjecture on Cantor Julia sets. Sci. China Ser. A 52 (2009), 45–65.CrossRefGoogle Scholar
Roeder, R.. Topology for the basins of attraction of Newton’s method in two complex variables: linking with currents. J. Geom. Anal. 17(1) (2007), 107–146.CrossRefGoogle Scholar
Roesch, P.. On local connectivity for the Julia set of rational maps: Newton’s famous example. Ann. of Math. (2) 165 (2008), 1–48.Google Scholar
Rückert, J. and Schleicher, D.. On Newton’s method for entire functions. J. Lond. Math. Soc. (2) 75(3) (2007), 659–676.CrossRefGoogle Scholar
Roesch, P., Wang, X. and Yin, Y.. Moduli space of cubic Newton maps. Adv. Math. 322 (2017), 1–59.CrossRefGoogle Scholar
Roesch, P. and Yin, Y.. Bounded critical Fatou components are Jordan domains for polynomials. Sci. China Math. 65 (2022), 331–358.Google Scholar
Shishikura, M.. The connectivity of the Julia set and fixed points. Complex Dynamics: Families and Friends. Ed. Schleicher, D.. A. K. Peters, Wellesley, MA, 2009.Google Scholar
Tan, L.. Branched coverings and cubic Newton maps. Fund. Math. 154(3) (1997), 207–260.CrossRefGoogle Scholar
Tan, L. and Yin, Y.. Local connectivity of the Julia set for geometrically finite rational maps. Sci. China Ser. A 39(1) (1996), 39–47, with an appendix prepublication in Rapport de Recherche UMPA, no. 121 (1994), Ecole Normale Superieure de Lyon.Google Scholar
Wolff, J.. Sur l’itération des fonctions holomorphes dans une région, et dont les valeurs appartiennent a cette région. C. R. Math. Acad. Sci. Paris 182 (1926), 42–43.Google Scholar