Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-29T13:41:37.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension approximation in smooth dynamical systems

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  11 April 2023

YONGLUO CAO ,
JUAN WANG  and
YUN ZHAO
YONGLUO CAO
Affiliation:
Departament of Mathematics, Soochow University, Suzhou 215006, Jiangsu, PR China (e-mail: [email protected]) Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou 215006, Jiangsu, PR China
JUAN WANG
Affiliation:
School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai 201620, PR China (e-mail: [email protected])
YUN ZHAO*
Affiliation:
Departament of Mathematics, Soochow University, Suzhou 215006, Jiangsu, PR China (e-mail: [email protected]) Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou 215006, Jiangsu, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a non-conformal repeller 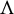$\Lambda $ of a 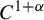$C^{1+\alpha }$ map f preserving an ergodic measure 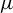$\mu $ of positive entropy, this paper shows that the Lyapunov dimension of 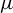$\mu $ can be approximated gradually by the Carathéodory singular dimension of a sequence of horseshoes. For a 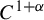$C^{1+\alpha }$ diffeomorphism f preserving a hyperbolic ergodic measure 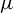$\mu $ of positive entropy, if 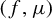$(f, \mu )$ has only two Lyapunov exponents 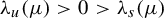$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$, then the Hausdorff or lower box or upper box dimension of 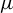$\mu $ can be approximated by the corresponding dimension of the horseshoes 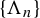$\{\Lambda _n\}$. The same statement holds true if f is a 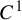$C^1$ diffeomorphism with a dominated Oseledet’s splitting with respect to 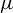$\mu $.

Keywords

dimensionhyperbolic measurehorseshoerepeller

MSC classification

Primary: 37C45: Dimension theory of dynamical systems 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Secondary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 2 , February 2024 , pp. 383 - 407
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alexander, J. C. and Yorke, J. A.. Fat Baker’s transformations. Ergod. Th. & Dynam. Sys. 4 (1984), 1–23.10.1017/S0143385700002236CrossRefGoogle Scholar
Avila, A., Crovisier, S. and Wilkinson, A.. ${C}^1$ density of stable ergodicity. Adv. Math. 379 (2021), Paper no. 107496, 68 pp.10.1016/j.aim.2020.107496CrossRefGoogle Scholar
Ban, J., Cao, Y. and Hu, H.. The dimensions of a non-conformal repeller and an average conformal repeller. Trans. Amer. Math. Soc. 362 (2010), 727–751.10.1090/S0002-9947-09-04922-8CrossRefGoogle Scholar
Barreira, L.. A non-additive thermodynamic formalism and applications to dimension theory of hyperbolic dynamical systems. Ergod. Th. & Dynam. Sys. 16 (1996), 871–928.10.1017/S0143385700010117CrossRefGoogle Scholar
Barreira, L.. Dimension and Recurrence in Hyperbolic Dynamics (Progress in Mathematics, 272). Birkh $\ddot{\mathrm{a}}$ user Verlag, Basel, 2008.Google Scholar
Barreira, L. and Pesin, Y.. Introduction to Smooth Ergodic Theory (Graduate Studies in Mathematics, 148). American Mathematical Society, Providence, RI, 2013.10.1090/gsm/148CrossRefGoogle Scholar
Barreira, L., Pesin, Y. and Schmeling, J.. Dimension and product structure of hyperbolic measures. Ann. of Math. (2) 149(3) (1999), 755–783.10.2307/121072CrossRefGoogle Scholar
Burns, K. and Wilkinson, A.. A note on stable holonomy between centers (preliminary version). Preprint, 2005, http://www.math.uchicago.edu/wilkinso/papers/c1hol0611.pdf.Google Scholar
Cao, Y., Feng, D. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20 (2008), 639–657.CrossRefGoogle Scholar
Cao, Y., Hu, H. and Zhao, Y.. Nonadditive measure-theoretic pressure and applications to dimensions of an ergodic measure. Ergod. Th. & Dynam. Sys. 33 (2013), 831–850.10.1017/S0143385712000090CrossRefGoogle Scholar
Cao, Y., Pesin, Y. and Zhao, Y.. Dimension estimates for non-conformal repellers and continuity of sub-additive topological pressure. Geom. Funct. Anal. 29 (2019), 1325–1368.10.1007/s00039-019-00510-7CrossRefGoogle Scholar
Chung, Y.. Shadowing properties of non-invertible maps with hyperbolic measures. Tokyo J. Math. 22 (1999), 145–166.10.3836/tjm/1270041619CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. Wiley, New York, 2003.10.1002/0470013850CrossRefGoogle Scholar
Feng, D. and Huang, W.. Variational principle for weighted topological pressure. J. Math. Pures Appl. (9) 106 (2016), 411–452.10.1016/j.matpur.2016.02.016CrossRefGoogle Scholar
Feng, D. and Simon, K.. Dimension estimates for ${C}^1$ iterated function systems and repellers. Part I. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2022.41. Published online 17 June 2022.CrossRefGoogle Scholar
Gelfert, K.. Repellers for non-uniformly expanding maps with singular or critical points. Bull. Braz. Math. Soc. (N.S.) 41 (2010), 237–257.10.1007/s00574-010-0012-1CrossRefGoogle Scholar
Gelfert, K.. Horseshoes for diffeomorphisms preserving hyperbolic measures. Math. Z. 283 (2016), 685–701.CrossRefGoogle Scholar
Hirsch, M. and Pugh, C.. Stable manifolds and hyperbolic sets. Global Analysis (Berkeley, CA, 1968) (Proc. Symp. Pure Math., XIV). American Mathematical Society, Providence, RI, 1970, pp. 133–163.Google Scholar
Kaplan, J. L. and Yorke, J. A.. Chaotic behavior of multidimensional differential equations. Functional Differential Equations and Approximations of Fixed Points (Lecture Notes in Mathematics, 730). Eds. Peitgen, H. and Walther, H.. Springer, Berlin, 1979, pp. 204–227.10.1007/BFb0064319CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54). Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511809187CrossRefGoogle Scholar
Ledrappier, F.. Some relations between dimension and Lyapunov exponents. Comm. Math. Phys. 81 (1981), 229–238.CrossRefGoogle Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension. Ann. of Math. (2) 122(3) (1985), 540–574.10.2307/1971329CrossRefGoogle Scholar
Luzzatto, S. and Sanchez-Salas, F. J.. Uniform hyperbolic approximation of measures with non-zero Lyapunov exponents. Proc. Amer. Math. Soc. 141 (2013), 3157–3169.10.1090/S0002-9939-2013-11565-0CrossRefGoogle Scholar
Mendoza, L.. The entropy of ${C}^2$ surface diffeomorphisms in terms of Hausdorff dimension and a Lyapunov exponent. Ergod. Th. & Dynam. Sys. 5 (1985), 273–283.10.1017/S0143385700002893CrossRefGoogle Scholar
Mendoza, L.. Ergodic attractors for diffeomorphisms of surfaces. J. Lond. Math. Soc. (2) 37 (1988), 362–374.CrossRefGoogle Scholar
Mendoza, L.. Topological entropy of homoclinic closures. Trans. Amer. Math. Soc. 311 (1989), 255–266.CrossRefGoogle Scholar
Misiurewicz, M. and Szlenk, W.. Entropy of piecewise monotone mappings. Studia Math. 67 (1980), 45–63.CrossRefGoogle Scholar
Morris, I. and Shmerkin, P.. On equality of Hausdorff and affinity dimensions via self-affine measures on positive subsystems. Trans. Amer. Math. Soc. 371 (2019), 1547–1582.10.1090/tran/7334CrossRefGoogle Scholar
Oseledec, V. I.. A multiplicative ergodic theorem. Characteristic Lyapnov exponents of dynamical systems. Tr. Moskov. Mat. Obšž 19 (1968), 179–210.Google Scholar
Palis, J. and Viana, M.. On the continuity of Hausdorff dimension and limit capacity for horseshoes. Dynamical Systems (Valparaiso, 1986) (Lecture Notes in Mathematics, 1331). Eds. Bamón, R., Labarca, R. and Palis, J.. Springer, Berlin, 1988, pp. 150–160.CrossRefGoogle Scholar
Persson, T. and Schmeling, J.. Dyadic diophantine approximation and Katok’s horseshoe approximation. Acta Arith. 132 (2008), 205–230.CrossRefGoogle Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems (Contemporary Views and Applications) (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 1997.CrossRefGoogle Scholar
Przytycki, F. and Urbański, M.. Conformal Fractals: Ergodic Theory Methods (London Mathematical Society Lecture Note Series, 371). Cambridge University Press, Cambridge, 2010.10.1017/CBO9781139193184CrossRefGoogle Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Hölder Foliations. Duke Math. J. 86(3), 517–546 (1997).10.1215/S0012-7094-97-08616-6CrossRefGoogle Scholar
Sánchez-Salas, F. J.. Ergodic attractors as limits of hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 22 (2002), 571–589.CrossRefGoogle Scholar
Sánchez-Salas, F. J.. Dimension of Markov towers for non-uniformly expanding one-dimensional systems. Discrete Contin. Dyn. Syst. 9 (2003), 1447–1464.CrossRefGoogle Scholar
Sánchez-Salas, F. J.. On the approximation of dynamical indicators in systems with nonuniformly hyperbolic behavior. Monatsh. Math. 182 (2017), 463–487.10.1007/s00605-016-0989-7CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer-Verlag, New York, 1982.10.1007/978-1-4612-5775-2CrossRefGoogle Scholar
Wang, J. and Cao, Y.. The Hausdorff dimension estimation for an ergodic hyperbolic measure of ${C}^1$ -diffeomorphism. Proc. Amer. Math. Soc. 144 (2016), 119–128.10.1090/proc/12696CrossRefGoogle Scholar
Wang, J., Cao, Y. and Zou, R.. The approximation of uniform hyperbolicity for ${C}^1$ -diffeomorphisms with hyperbolic measures. J. Differential Equations 275 (2021), 359–390.CrossRefGoogle Scholar
Wang, J., Qu, C. and Cao, Y.. Dimension approximation for diffeomorphisms preserving hyperbolic SRB measures. J. Differential Equations 337 (2022), 294–322.CrossRefGoogle Scholar
Wang, J., Wang, J., Cao, Y. and Zhao, Y.. Dimensions of ${C}^1$ -average conformal hyperbolic sets. Discrete Contin. Dyn. Syst. 40(2) (2020), 883–905.10.3934/dcds.2020065CrossRefGoogle Scholar
Yang, Y.. Horseshoes for ${C}^{1+\alpha }$ mappings with hyperbolic measures. Discrete Contin. Dyn. Syst. 35 (2015), 5133–5152.10.3934/dcds.2015.35.5133CrossRefGoogle Scholar
Young, L. S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 109–129.10.1017/S0143385700009615CrossRefGoogle Scholar
Zhao, Y.. Measure-theoretic pressure for amenable group actions. Colloq. Math. 148(1) (2017), 87–106.10.4064/cm6784-6-2016CrossRefGoogle Scholar