Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-30T09:28:47.672Z Has data issue: false hasContentIssue false
  • English
  • Français

PIN(2)-monopole Floer homology and the Rokhlin invariant

Part of: Low-dimensional topology Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  08 November 2018

Francesco Lin
Francesco Lin*
Affiliation:
Department of Mathematics, Princeton University and Institute for Advanced Study, Princeton, NJ 08540, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the bar version of the 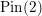$\text{Pin}(2)$-monopole Floer homology of a three-manifold 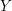$Y$ equipped with a self-conjugate spin$^{c}$ structure $\mathfrak{s}$ is determined by the triple cup product of 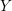$Y$ together with the Rokhlin invariants of the spin structures inducing $\mathfrak{s}$. This is a manifestation of mod 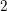$2$ index theory and can be interpreted as a three-dimensional counterpart of Atiyah’s classical results regarding spin structures on Riemann surfaces.

Keywords

monopole Floer homologyquaternionic operatorsRokhlin invariant

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Secondary: 58J20: Index theory and related fixed point theorems
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 12 , December 2018 , pp. 2681 - 2700
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Atiyah, M. F., K-theory and reality , Q. J. Math. Oxford Ser. (2) 17 (1966), 367–386.Google Scholar
Atiyah, M. F., K-theory, Lecture Notes by D. W. Anderson (W. A. Benjamin, New York–Amsterdam, 1967).Google Scholar
Atiyah, M. F., Riemann surfaces and spin structures , Ann. Sci. Éc. Norm. Supér. (4) 4 (1971), 47–62.Google Scholar
Atiyah, M. F., Bott, R. and Shapiro, A., Clifford modules , Topology 3 (1964), 3–38.Google Scholar
Atiyah, M. F., Patodi, V. K. and Singer, I. M., Spectral asymmetry and Riemannian geometry. III , Math. Proc. Cambridge Philos. Soc. 79 (1976), 71–99.Google Scholar
Atiyah, M. F. and Singer, I. M., Index theory for skew-adjoint Fredholm operators , Publ. Math. Inst. Hautes Études Sci. 37 (1969), 5–26.Google Scholar
Atiyah, M. F. and Singer, I. M., The index of elliptic operators. IV , Ann. of Math. (2) 93 (1971), 119–138.Google Scholar
Atiyah, M. F. and Singer, I. M., The index of elliptic operators. V , Ann. of Math. (2) 93 (1971), 139–149.Google Scholar
Dupont, J. L., Symplectic bundles and KR-theory , Math. Scand. 24 (1969), 27–30.Google Scholar
Furuta, M. and Kametani, Y., Equivariant maps between sphere bundles over tori and $ko^{\ast }$ degree, Preprint (2005), arXiv:0502511.Google Scholar
Hatcher, A., Algebraic topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Kirby, R. C., The topology of 4-manifolds, Lecture Notes in Mathematics, vol. 1374 (Springer, Berlin, 1989).Google Scholar
Kronheimer, P. and Mrowka, T., Monopoles and three-manifolds, New Mathematical Monographs, vol. 10 (Cambridge University Press, Cambridge, 2007).Google Scholar
Li, T.-J., Quaternionic bundles and Betti numbers of symplectic 4-manifolds with Kodaira dimension zero , Int. Math. Res. Not. IMRN 2006 (2006), Art. ID 37385, 28 pp.Google Scholar
Lin, F., A Morse–Bott approach monopole Floer homology and the triangulation conjecture , Mem. Amer. Math. Soc. 255(1221) (2018).Google Scholar
Lin, F., Lectures on monopole Floer homology , in Proceedings of the Gökova geometry-topology conference 2015 (International Press, Boston, MA, 2016), 39–80.Google Scholar
Lin, F., Pin(2)-monopole Floer homology, higher compositions and connected sums , J. Topol. 10 (2017), 921–969.Google Scholar
Manolescu, C., The Conley index, gauge theory, and triangulations , J. Fixed Point Theory Appl. 13 (2013), 431–457.Google Scholar
Manolescu, C., Pin(2)-equivariant Seiberg–Witten Floer homology and the triangulation conjecture , J. Amer. Math. Soc. 29 (2016), 147–176.Google Scholar
Milnor, J., Morse theory, Based on Lecture Notes by M. Spivak and R. Wells. Annals of Mathematics Studies, vol. 51 (Princeton University Press, Princeton, NJ, 1963).Google Scholar
Ruberman, D. and Strle, S., Mod 2 Seiberg–Witten invariants of homology tori , Math. Res. Lett. 7 (2000), 789–799.Google Scholar
Taubes, C. H., The Seiberg–Witten equations and the Weinstein conjecture , Geom. Topol. 11 (2007), 2117–2202.Google Scholar