Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-30T03:33:41.888Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  13 September 2024

Masaaki Furusawa Open the ORCID record for Masaaki Furusawa [Opens in a new window]  and
Kazuki Morimoto Open the ORCID record for Kazuki Morimoto [Opens in a new window]
Masaaki Furusawa
Affiliation:
Department of Mathematics, Graduate School of Science, Osaka Metropolitan University, Sugimoto 3-3-138, Sumiyoshi-ku, Osaka 558-8585, Japan [email protected]
Kazuki Morimoto
Affiliation:
Department of Mathematics, Graduate School of Science, Kobe University, 1-1 Rokkodai-cho, Nada-ku, Kobe 657-8501, Japan [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the Gross–Prasad conjecture and its refinement for the Bessel periods in the case of 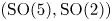$(\mathrm {SO}(5), \mathrm {SO}(2))$. In particular, by combining several theta correspondences, we prove the Ichino–Ikeda-type formula for any tempered irreducible cuspidal automorphic representation. As a corollary of our formula, we prove an explicit formula relating certain weighted averages of Fourier coefficients of holomorphic Siegel cusp forms of degree two, which are Hecke eigenforms, to central special values of 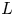$L$-functions. The formula is regarded as a natural generalization of the Böcherer conjecture to the non-trivial toroidal character case.

Keywords

Böcherer conjecturecentral L-valuesGross–Prasad conjectureperiods of automorphic forms

MSC classification

Primary: 11F55: Other groups and their modular and automorphic forms (several variables) 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Secondary: 11F27: Theta series; Weil representation; theta correspondences 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 9 , September 2024 , pp. 2115 - 2202
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, J. and Barbasch, D., Reductive dual pair correspondence for complex groups, J. Funct. Anal. 132 (1995), 1–42.CrossRefGoogle Scholar
Arthur, J., The endoscopic classification of representations. Orthogonal and symplectic groups, Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013).Google Scholar
Arthur, J. and Clozel, L., Simple algebras, base change and the advanced theory of the trace formula, Annals of Mathematics Studies, vol. 120 (Princeton University Press, Princeton, NJ, 1989).Google Scholar
Atobe, H., On the uniqueness of generic representations in an $L$-packet, Int. Math. Res. Not. IMRN 2017 (2017), 7051–7068.Google Scholar
Atobe, H. and Gan, W. T., Local theta correspondence of tempered representations and Langlands parameters, Invent. Math. 210 (2017), 341–415.CrossRefGoogle Scholar
Beuzart-Plessis, R., La conjecture locale de Gross–Prasad pour les représentations tempérées des groupes unitaires, Mém. Soc. Math. Fr. (N.S.) 2016 (2016).Google Scholar
Beuzart-Plessis, R., A local trace formula for the Gan–Gross–Prasad conjecture for unitary groups: the Archimedean case, Astérisque 418 (2020).Google Scholar
Beuzart-Plessis, R. and Chaudouard, P.-H., The global Gan–Gross–Prasad conjecture for unitary groups. II. From Eisenstein series to Bessel periods, Preprint (2023), arXiv:2302.12331.Google Scholar
Beuzart-Plessis, R., Chaudouard, P.-H. and Zydor, M., The global Gan–Gross–Prasad conjecture for unitary groups: the endoscopic case, Publ. Math. Inst. Hautes Études Sci. 135 (2022), 183–336.CrossRefGoogle Scholar
Beuzart-Plessis, R., Liu, Y., Zhang, W. and Zhu, X., Isolation of cuspidal spectrum, with application to the Gan–Gross–Prasad conjecture, Ann. of Math. (2) 194 (2021), 519–584.CrossRefGoogle Scholar
Blasius, D., Hilbert modular forms and the Ramanujan conjecture, in Noncommutative geometry and number theory, Aspects of Mathematics, vol. E37 (Vieweg, Wiesbaden, 2006), 35–56.CrossRefGoogle Scholar
Blomer, V., Spectral summation formula for $\mathrm {GSp}(4)$ and moments of spinor $L$-functions, J. Eur. Math. Soc. (JEMS) 21 (2019), 1751–1774.CrossRefGoogle Scholar
Böcherer, S., Bemerkungen über die Dirichletreihen von Koecher und Maaß, Mathematica Gottingensis, vol. 68 (Georg-August University, Göttingen, 1986), 36.Google Scholar
Cai, Y., Friedberg, S. and Kaplan, E., Doubling constructions: global functoriality for non-generic cuspidal representations, Ann. of Math., to appear. Preprint (2018), arXiv:1802.02637.Google Scholar
Caraiani, A., Local-global compatibility and the action of monodromy on nearby cycles, Duke Math. J. 161 (2012), 2311–2413.CrossRefGoogle Scholar
Chan, P.-S., Invariant representations of GSp(2) under tensor product with a quadratic character, Mem. Amer. Math. Soc. 204 (2010).Google Scholar
Chen, S.-Y. and Ichino, A., On Petersson norms of generic cusp forms and special values of adjoint $L$-functions for $\mathrm {GSp}_4$, Amer. J. Math. 145 (2023), 899–993.CrossRefGoogle Scholar
Chida, M. and Hsieh, M.-L., Special values of anticyclotomic $L$-functions for modular forms, J. Reine Angew. Math. 741 (2018), 87–131.CrossRefGoogle Scholar
Cogdell, J. W., Kim, H. H., Piatetski-Shapiro, I. I. and Shahidi, F., Functoriality for the classical groups, Publ. Math. Inst. Hautes Études Sci. 99 (2004), 163–233.CrossRefGoogle Scholar
Corbett, A., A proof of the refined Gan–Gross–Prasad conjecture for non-endoscopic Yoshida lifts, Forum Math. 29 (2017), 59–90.CrossRefGoogle Scholar
Dickson, M., Pitale, A., Saha, A. and Schmidt, R., Explicit refinements of Böcherer's conjecture for Siegel modular forms of squarefree level, J. Math. Soc. Japan 72 (2020), 251–301.CrossRefGoogle Scholar
Dummigan, N., Congruences of Saito–Kurokwa lifts and denominators of central special $L$-values, Glasg. Math. J. 64 (2022), 504–525.CrossRefGoogle Scholar
Furusawa, M., On the theta lift from $\mathrm {SO}_{2n+1}$ to $\widetilde {\mathrm {Sp}}_n$, J. Reine Angew. Math. 466 (1995), 87–110.Google Scholar
Furusawa, M. and Martin, K., On central critical values of the degree four L-functions for $\mathrm {GSp}(4)$: the fundamental lemma. II, Amer. J. Math. 133 (2011), 197–233.CrossRefGoogle Scholar
Furusawa, M. and Martin, K., On central critical values of the degree four L-functions for $\mathrm {GSp}(4)$: the fundamental lemma. III, Mem. Amer. Math. Soc. 225 (2013).Google Scholar
Furusawa, M. and Morimoto, K., Shalika periods on $\mathrm {GU}(2, 2)$, Proc. Amer. Math. Soc. 141 (2013), 4125–4137.CrossRefGoogle Scholar
Furusawa, M. and Morimoto, K., On special Bessel periods and the Gross–Prasad conjecture for $\mathrm {SO}(2n+1) \times \mathrm {SO}(2)$, Math. Ann. 368 (2017), 561–586.CrossRefGoogle Scholar
Furusawa, M. and Morimoto, K., Refined global Gross–Prasad conjecture on special Bessel periods and Böcherer's conjecture, J. Eur. Math. Soc. (JEMS) 23 (2021), 1295–1331.CrossRefGoogle Scholar
Furusawa, M. and Morimoto, K., On the Gan–Gross–Prasad conjecture and its refinement for $(\mathrm {U}(2n), \mathrm {U}(1))$, Preprint (2022), arXiv:2205.09471.Google Scholar
Furusawa, M. and Shalika, J., On central critical values of the degree four L-functions for $\mathrm {GSp}(4)$: the fundamental lemma, Mem. Amer. Math. Soc. 164 (2003).Google Scholar
Gan, W. T., The Saito–Kurokawa space of PGSp 4 and its transfer to inner forms, in Eisenstein Series and Applications, Progress in Mathematics, vol. 258 (Birkhäuser, Boston, MA, 2008), 87–123.CrossRefGoogle Scholar
Gan, W. T., Gross, B. and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups, in Sur les conjectures de Gross et Prasad. I, Astérisque, vol. 346 (Société mathématique de France, 2012), 1–109.Google Scholar
Gan, W. T. and Ichino, A., On endoscopy and the refined Gross–Prasad conjecture for $(\mathrm {SO}_5,\mathrm {SO}_4)$, J. Inst. Math. Jussieu 10 (2011), 235–324.CrossRefGoogle Scholar
Gan, W. T. and Ichino, A., Formal degrees and local theta correspondence, Invent. Math. 195 (2014), 509–672.CrossRefGoogle Scholar
Gan, W. T., Qiu, Y. and Takeda, S., The regularized Siegel–Weil formula (the second term identity) and the Rallis inner product formula, Invent. Math. 198 (2014), 739–831.CrossRefGoogle Scholar
Gan, W. T. and Sun, B., The Howe duality conjecture: quaternionic case, in Representation theory, number theory, and invariant theory, Progress in Mathematics, vol. 323 (Birkhäuser, Cham, 2017), 175–192.CrossRefGoogle Scholar
Gan, W. T. and Takeda, S., On Shalika periods and a theorem of Jacquet–Martin, Amer. J. Math. 132 (2010), 475–528.CrossRefGoogle Scholar
Gan, W. T. and Takeda, S., The local Langlands conjecture for $\mathrm {GSp}(4)$, Ann. of Math. (2) 173 (2011), 1841–1882.CrossRefGoogle Scholar
Gan, W. T. and Takeda, S., Theta correspondences for $\mathrm {GSp}(4)$, Represent. Theory 15 (2011), 670–718.CrossRefGoogle Scholar
Gan, W. T. and Takeda, S., A proof of the Howe duality conjecture, J. Amer. Math. Soc. 29 (2016), 473–493.CrossRefGoogle Scholar
Gan, W. T. and Tantono, W., The local Langlands conjecture for $\mathrm {GSp}(4)$, II: The case of inner forms, Amer. J. Math. 136 (2014), 761–805.CrossRefGoogle Scholar
Ginzburg, D., Rallis, S. and Soudry, D., Periods, poles of L-functions and symplectic-orthogonal theta lifts, J. Reine Angew. Math. 487 (1997), 85–114.Google Scholar
Ginzburg, D., Rallis, S. and Soudry, D., The descent map from automorphic representations of GL(n) to classical groups (World Scientific, Hackensack, NJ, 2011).CrossRefGoogle Scholar
Gross, B. and Prasad, D., On the decomposition of a representation of $\mathrm {SO}_n$ when restricted to $\mathrm {SO}_{n-1}$, Canad. J. Math. 44 (1992), 974–1002.CrossRefGoogle Scholar
Gross, B. and Prasad, D., On irreducible representations of $\mathrm {SO}_{2n+1} \times \mathrm {SO}_{2m}$, Canad. J. Math. 46 (1994), 930–950.CrossRefGoogle Scholar
Harris, M. and Kudla, S., Arithmetic automorphic forms for the nonholomorphic discrete series of ${\rm GSp}(2)$, Duke Math. J. 66 (1992), 59–121.CrossRefGoogle Scholar
Harris, M., Soudry, D. and Taylor, R., $\ell$-adic representations associated to modular forms over imaginary quadratic fields. I. Lifting to $\mathrm {GSp}_4(\mathbb {Q})$, Invent. Math. 112 (1993), 377–411.CrossRefGoogle Scholar
Harris, N., The refined Gross–Prasad conjecture for unitary groups, Int. Math. Res. Not. IMRN 2014 (2014), 303–389.CrossRefGoogle Scholar
Hiraga, K., Ichino, A. and Ikeda, T., Formal degrees and adjoint $\gamma$-factors, J. Amer. Math. Soc. 21 (2008), 283–304.CrossRefGoogle Scholar
Hiraga, K., Ichino, A. and Ikeda, T., Correction to: ‘Formal degrees and adjoint $\gamma$-factors’, J. Amer. Math. Soc. 21 (2008), 1211–1213.CrossRefGoogle Scholar
Hiraga, K. and Saito, H., On $L$-packets for inner forms of $\mathrm {SL}_n$, Mem. Amer. Math. Soc. 215 (2012).Google Scholar
Howe, R., Transcending classical invariant theory, J. Amer. Math. Soc. 2 (1989), 535–552.CrossRefGoogle Scholar
Hsieh, M.-L. and Namikawa, K., Bessel periods and the non-vanishing of Yoshida lifts modulo a prime, Math. Z. 285 (2017), 851–878.CrossRefGoogle Scholar
Hsieh, M.-L. and Namikawa, K., Inner product formula for Yoshida lifts, Ann. Math. Qué. 42 (2018), 215–253.CrossRefGoogle Scholar
Hsieh, M.-L. and Yamana, S., Bessel periods and anticyclotomic p-adic spinor $L$-functions, Trans. Amer. Math. Soc. 377 (2024), 5617–5672.Google Scholar
Ichino, A., Trilinear forms and the central values of triple product L-functions, Duke Math. J. 145 (2008), 281–307.CrossRefGoogle Scholar
Ichino, A. and Ikeda, T., On the periods of automorphic forms on special orthogonal groups and the Gross–Prasad conjecture, Geom. Funct. Anal. 19 (2010), 1378–1425.CrossRefGoogle Scholar
Ichino, A. and Prasanna, K., Periods of quaternionic Shimura varieties. I, Contemporary Mathematics, vol. 762 (American Mathematical Society, Providence, RI, 2021).CrossRefGoogle Scholar
Ishimoto, H., The endoscopic classification of representations of non-quasi-split odd special orthogonal groups, Int. Math. Res. Not. IMRN 2024 (2024), 10939–11012.CrossRefGoogle Scholar
Iwaniec, H., Luo, W. and Sarnak, P., Low Lying zeros of families of $L$-functions, Publ. Math. Inst. Hautes Études Sci. 91 (2000), 55–131.CrossRefGoogle Scholar
Jacquet, H., Distinction by the quasi-split unitary group, Israel J. Math. 178 (2010), 269–324.CrossRefGoogle Scholar
Jiang, D., Sun, B. and Zhu, C.-B., Uniqueness of Bessel models: the Archimedean case, Geom. Funct. Anal. 20 (2010), 690–709.CrossRefGoogle Scholar
Jiang, D. and Zhang, L., Arthur parameters and cuspidal automorphic modules of classical groups, Ann. of Math. (2) 191 (2020), 739–827.CrossRefGoogle Scholar
Jorza, A., Galois representations for holomorphic Siegel modular forms, Math. Ann. 355 (2013), 381–400.CrossRefGoogle Scholar
Kaletha, T., Minguez, A., Shin, S. W. and White, P. J., Endoscopic classification of representations: Inner forms of unitary groups, Preprint (2014), arXiv:1409.3731.Google Scholar
Kemarsky, A., A note on the Kirillov model for representations of $\mathrm {GL}_n(\mathbb {C})$, C. R. Math. Acad. Sci. Paris 353 (2015), 579–582.CrossRefGoogle Scholar
Kudla, S., On the local theta-correspondence, Invent. Math. 83 (1986), 229–255.CrossRefGoogle Scholar
Kudla, S., Splitting metaplectic covers of dual reductive pairs, Israel J. Math. 87 (1994), 361–401.CrossRefGoogle Scholar
Kutzko, P., The Langlands conjecture for $\mathrm {Gl}_2$ of a local field, Ann. of Math. (2) 112 (1980), 381–412.CrossRefGoogle Scholar
Langlands, R. P., On the classification of irreducible representations of real algebraic groups, Representation theory and harmonic analysis on semisimple Lie groups, Mathematical Surveys and Monographs, vol. 31 (American Mathematical Society, Providence, RI, 1989), 101–170.Google Scholar
Lapid, E. and Mao, Z., A conjecture on Whittaker–Fourier coefficients of cusp forms, J. Number Theory 146 (2015), 448–505.CrossRefGoogle Scholar
Lapid, E. and Mao, Z., On an analogue of the Ichino–Ikeda conjecture for Whittaker coefficients on the metaplectic group, Algebra Number Theory 11 (2017), 713–765.CrossRefGoogle Scholar
Lapid, E. and Rallis, S., On the local factors of representations of classical groups, in Automorphic representations, L-functions and applications: progress and prospects, Ohio State University Mathematical Research Institute Publications, vol. 11 (de Gruyter, Berlin, 2005), 309–359.CrossRefGoogle Scholar
Li, J.-S., Nonexistence of singular cusp forms, Compos. Math. 83 (1992), 43–51.Google Scholar
Li, J.-S., Paul, A., Tan, E.-C. and Zhu, C.-B., The explicit duality correspondence of $(\mathrm {Sp}(p,q),\mathrm {O}^\ast (2n))$, J. Funct. Anal. 200 (2003), 71–100.CrossRefGoogle Scholar
Liu, Y., Refined Gan–Gross–Prasad conjecture for Bessel periods, J. Reine Angew. Math. 717 (2016), 133–194.CrossRefGoogle Scholar
Luo, Z., A local trace formula for the local Gan–Gross–Prasad conjecture for special orthogonal groups, Preprint (2020), arXiv:2009.13947.Google Scholar
Martin, K. and Whitehouse, D., Central values and toric periods for $\mathrm {GL}(2)$, Int. Math. Res. Not. IMRN 2009 (2009), 141–191.CrossRefGoogle Scholar
Michel, P. and Ramakrishnan, D., Consequences of the Gross-Zagier formulae: stability of average L-values, subconvexity, and non-vanishing mod p, in Number theory, analysis and geometry (Springer, New York, 2012), 437–459.CrossRefGoogle Scholar
Mœglin, C., Correspondance de Howe pour les paires reductives duales: quelques calculs dans le cas archimédien, J. Funct. Anal. 85 (1989), 1–85.CrossRefGoogle Scholar
Mœglin, C., Vigneras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics, vol. 1291 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Mok, C. P., Endoscopic classification of representations of quasi-split unitary groups, Mem. Amer. Math. Soc. 235 (2015).Google Scholar
Morimoto, K., On the theta correspondence for $(\mathrm {GSp}(4),\mathrm {GSO}(4,2))$ and Shalika periods, Represent. Theory 18 (2014), 28–87.CrossRefGoogle Scholar
Morimoto, K., On $L$-functions for quaternion unitary groups of degree $2$ and $\mathrm {GL}(2)$ (with an Appendix by M. Furusawa and A. Ichino), Int. Math. Res. Not. IMRN 2014 (2014), 1729–1832.Google Scholar
Paul, A., Howe correspondence for real unitary groups, J. Funct. Anal. 159 (1998), 384–431.CrossRefGoogle Scholar
Paul, A., Howe correspondence for real unitary groups. II, Proc. Amer. Math. Soc. 128 (2000), 3129–3136.CrossRefGoogle Scholar
Paul, A., On the Howe correspondence for symplectic–orthogonal dual pairs, J. Funct. Anal. 228 (2005), 270–310.CrossRefGoogle Scholar
Piatetski-Shapiro, I. I. and Rallis, S., L-functions for the classical groups, in Explicit constructions of automorphic L-functions, Lecture Notes in Mathematics, vol. 1254, 1–52.Google Scholar
Pitale, A., Saha, A. and Schmidt, R., Transfer of Siegel cusp forms of degree 2, Mem. Amer. Math. Soc. 232 (2014).Google Scholar
Pitale, A., Saha, A. and Schmidt, R., Simple supercuspidal representations of $\mathrm {GSp}_4$ and test vectors, Preprint (2023), arXiv:2302.05148Google Scholar
Prasad, D. and Ramakrishnan, D., On the global root numbers of $\mathrm {GL}(n) \times \mathrm {GL}(m)$, in Automorphic forms, automorphic representations, and arithmetic, Part 2, Proceedings of Symposia in Pure Mathematics, vol. 66 (American Mathematical Society, Providence, RI, 1999), 311–330.CrossRefGoogle Scholar
Prasad, D. and Takloo-Bighash, R., Bessel models forv GSp(4), J. Reine Angew. Math. 655 (2011), 189–243.Google Scholar
Raghuram, A. and Sarnobat, M., Cohomological representations and functorial transfer from classical groups, in Cohomology of arithmetic group, Springer Proceedings in Mathematics and Statistics, vol. 245 (Springer, Cham, 2018), 157–176.CrossRefGoogle Scholar
Ramakrishnan, D. and Rogawski, J., Average values of modular $L$-series via the relative trace formula, Pure Appl. Math. Q. 1 (2005), 701–735.CrossRefGoogle Scholar
Roberts, B., The theta correspondence for similitudes, Israel J. Math. 94 (1996), 285–317.CrossRefGoogle Scholar
Roberts, B., Global L-packets for $\mathrm {GSp}(2)$ and theta lifts, Doc. Math. 6 (2001), 247–314.CrossRefGoogle Scholar
Saha, A., A relation between multiplicity one and Böcherer's conjecture, Ramanujan J. 33 (2014), 263–268.CrossRefGoogle Scholar
Saha, A., On ratios of Petersson norms for Yoshida lifts, Forum Math. 27 (2015), 2361–2412.CrossRefGoogle Scholar
Saha, A. and Schmidt, R., Yoshida lifts and simultaneous non-vanishing of dihedral twists of modular $L$-functions, J. London Math. Soc. 88 (2013), 251–270.CrossRefGoogle Scholar
Satake, I., Some remarks to the preceding paper of Tsukamoto, J. Math. Soc. Japan 13 (1961), 401–409.CrossRefGoogle Scholar
Schmidt, R., Iwahori-spherical representations of $\mathrm {GSp}(4)$ and Siegel modular forms of degree $2$ with square-free level, J. Math. Soc. Japan 57 (2005), 259–293.CrossRefGoogle Scholar
Shahidi, F., On certain $L$-functions, Amer. J. Math. 103 (1981), 297–355.CrossRefGoogle Scholar
Soudry, D., A uniqueness theorem for representations of $\mathrm {GSO}(6)$ and the strong multiplicity one theorem for generic representations of $\mathrm {GSp}(4)$, Israel J. Math. 58 (1987), 257–287.CrossRefGoogle Scholar
Sugano, T., On holomorphic cusp forms on quaternion unitary group of degree $2$, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 31 (1985), 521–568.Google Scholar
Sun, B. and Zhu, C.-B., Conservation relations for local theta correspondence, J. Amer. Math. Soc. 28 (2015), 939–983.CrossRefGoogle Scholar
Takeda, S., Some local-global non-vanishing results of theta lifts for symplectic-orthogonal dual pairs, J. Reine Angew. Math. 657 (2011), 81–111.Google Scholar
Tan, V., Poles of Siegel Eisenstein series on $\mathrm {U}(n, n)$, Canad. J. Math. 51 (1999), 164–175.CrossRefGoogle Scholar
Tsukamoto, T., On the local theory of quaternionic anti-hermitian forms, J. Math. Soc. Japan 13 (1961), 387–400.CrossRefGoogle Scholar
Varma, S., On descent and the generic packet conjecture, Forum Math. 29 (2017), 111–155.CrossRefGoogle Scholar
Vogan, D., Gel'fand-Kirillov dimension for Harish-Chandra modules, Invent. Math. 48 (1978), 75–98.CrossRefGoogle Scholar
Waibel, F., Moments of spinor $L$-functions and symplectic Kloosterman sums, Q. J. Math. 70 (2019), 1411–1436.Google Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions $L$ automorphes en leur centre de symétrie, Compos. Math. 54 (1985), 173–242.Google Scholar
Waldspurger, J.-L., Démonstration d'une conjecture de dualité de Howe dans le cas p-adique, p ≠ 2, in Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part I (Ramat Aviv, 1989), Israel Mathematics Conference Proceedings, vol. 2 (Weizmann, Jerusalem, 1990), 267–324.Google Scholar
Waldspurger, J.-L., Une formule intégrale reliée à la conjecture locale de Gross–Prasad, 2e partie: extension aux représentations tempérées, in Sur les conjectures de Gross et Prasad. I, Astérisque, vol. 346 (Société mathématique de France, 2012), 171–312.Google Scholar
Waldspurger, J.-L., La conjecture locale de Gross–Prasad pour les représentations tempérées des groupes spéciaux orthogonaux, in Sur les conjectures de Gross et Prasad. II, Astérisque, vol. 347 (Société mathématique de France, 2012), 103–165.Google Scholar
Weissauer, R., Endoscopy for GSp(4) and the cohomology of Siegel modular threefolds, Lecture Notes in Mathematics, vol. 1968 (Springer, Berlin, 2009).CrossRefGoogle Scholar
Xue, H., Refined global Gan–Gross–Prasad conjecture for Fourier–Jacobi periods on symplectic groups, Compos. Math. 153 (2017), 68–131.CrossRefGoogle Scholar
Xue, H., Bessel models for real unitary groups: the tempered case, Duke Math. J. 172 (2023), 995–1031.CrossRefGoogle Scholar
Yamana, S., The Siegel-Weil formula for unitary groups, Pacific J. Math. 264 (2013), 235–257.CrossRefGoogle Scholar
Yamana, S., $L$-functions and theta correspondence for classical groups, Invent. Math. 196 (2014), 651–732.CrossRefGoogle Scholar
Zhang, Z., A note on the local theta correspondence for unitary similitude dual pairs, J. Number Theory 133 (2013), 3057–3064.CrossRefGoogle Scholar