Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-29T02:59:45.107Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p

Part of: (Co)homology theory Arithmetic problems. Diophantine geometry Algebraic groups Symplectic geometry, contact geometry

Published online by Cambridge University Press:  05 January 2024

Ekaterina Bogdanova Open the ORCID record for Ekaterina Bogdanova [Opens in a new window]  and
Vadim Vologodsky
Ekaterina Bogdanova
Affiliation:
National Research University “Higher School of Economics”, Moscow 119048, Russia [email protected]
Vadim Vologodsky
Affiliation:
National Research University “Higher School of Economics”, Moscow 119048, Russia [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that after inverting the Planck constant 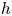$h$, the Bezrukavnikov–Kaledin quantization 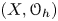$(X, {\mathcal {O}}_h)$ of symplectic variety 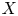$X$ in characteristic 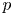$p$ with 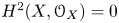$H^2(X, {\mathcal {O}}_X) =0$ is Morita equivalent to a certain central reduction of the algebra of differential operators on 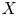$X$.

Keywords

deformation quantizationpositive characteristic

MSC classification

Primary: 14G17: Positive characteristic ground fields 53D55: Deformation quantization, star products
Secondary: 14L15: Group schemes 14F22: Brauer groups of schemes
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 2 , February 2024 , pp. 411 - 450
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beauville, A. and Laszlo, Y., Un lemme de descente, C. R. Acad. Sci. 320 (1995), 335–340.Google Scholar
Bezrukavnikov, R. and Braverman, A., Geometric Langlands correspondence for $D$-modules in prime characteristic: the $\operatorname {GL}(n)$ case, Pure Appl. Math. Q. 3 (2007), 153–179; Special Issue: In honor of Robert D. MacPherson. Part 3.CrossRefGoogle Scholar
Bezrukavnikov, R. and Finkelberg, M., Wreath Macdonald polynomials and categorical McKay correspondence, Camb. J. Math. 2 (2014), 163–190.CrossRefGoogle Scholar
Bezrukavnikov, R. and Kaledin, D., Fedosov quantization in algebraic context, Mosc. Math. J. 4 (2004), 559–592.CrossRefGoogle Scholar
Bezrukavnikov, R. and Kaledin, D., McKay equivalence for symplectic resolutions of singularities, Proc. Steklov Inst. Math. 246 (2004), 13–33.Google Scholar
Bezrukavnikov, R. and Kaledin, D., Fedosov quantization in positive characteristic, J. Amer. Math. Soc. 21 (2008), 409–438.CrossRefGoogle Scholar
Bezrukavnikov, R. and Losev, I., Etingof conjecture for quantized quiver varieties, Invent. Math. 223 (2021), 1097–1226.CrossRefGoogle Scholar
Bezrukavnikov, R., Mirkovic, I. and Rumynin, D., Localization of modules for a semisimple Lie algebra in prime characteristic, Ann. of Math. (2) 167 (2002), 945–991.CrossRefGoogle Scholar
Bogdanova, E., Kubrak, D., Travkin, R. and Vologodsky, V., The canonical global quantization of symplectic varieties in characteristic $p$, Preprint (2022), arXiv:2211.17261.Google Scholar
Borel, A., Linear Algebraic groups, Graduate Texts in Mathematics, vol. 126 (Springer, New York, 1991).CrossRefGoogle Scholar
Contou-Carrere, C., Jacobienne locale, groupe de bivecteurs de Witt universel, et symbole modere, C. R. Math. Acad. Sci. Paris 318 (1994), 743–746.Google Scholar
Demazure, M. and Gabriel, P., Introduction to algebraic geometry and algebraic groups, North-Holland Mathematics Studies, vol. 39 (North-Holland, 1980).Google Scholar
Grothendieck, A. and Dieudonne, J., Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents, Première partie. Étude globale élémentaire de quelques classes de morphismes, Publ. Math. Inst. Hautes Études Sci. 8 (1961), 222.Google Scholar
Kaledin, D., Derived equivalences by quantization, Geom. Funct. Anal. 17 (2008), 1968–2004.CrossRefGoogle Scholar
Katz, N., Algebraic solutions of differential equations ($p$-curvature and the Hodge filtration), Invent. Math. 18 (1972), 1–118.CrossRefGoogle Scholar
Kubrak, D. and Travkin, R., Resolutions with conical slices and descent for the Brauer group classes of certain central reductions of differential operators in characteristic $p$, Int. Math. Res. Not. IMRN 2019 (2019), rnz169.Google Scholar
Milne, J., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, 1980).Google Scholar
Molokov, S., Quantizations in characteristic $p$, Bachelor's thesis, HSE University (2017).Google Scholar
Mundinger, J., Quantization of restricted Lagrangian subvarieties in positive characteristic, Adv. Math. 410 (2022), Paper No. 108760.CrossRefGoogle Scholar
Ogus, A. and Vologodsky, V., Nonabelian Hodge theory in characteristic $p$, Publ. Math. Inst. Hautes Études Sci. 106 (2007), 1–138.CrossRefGoogle Scholar
The Stacks Project Authors. Stacks Project, https://stacks.math.columbia.edu.Google Scholar
Zhu, X., An introduction to affine Grassmannians and the geometric Satake equivalence, in Geometry of moduli spaces and representation theory, IAS/Park City Mathematics Series, vol. 24 (American Mathematical Society, Providence, RI, 2017), 59–154.CrossRefGoogle Scholar