Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-28T12:04:14.552Z Has data issue: false hasContentIssue false
  • English
  • Français

On some mod p representations of quaternion algebra over ℚp

Part of: Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  03 December 2024

Yongquan Hu Open the ORCID record for Yongquan Hu [Opens in a new window]  and
Haoran Wang Open the ORCID record for Haoran Wang [Opens in a new window]
Yongquan Hu
Affiliation:
Morningside Center of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences; University of the Chinese Academy of Sciences, Beijing 100190, PR China [email protected]
Haoran Wang
Affiliation:
Academy for Multidisciplinary Studies, Capital Normal University, Beijing 100048, PR China [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 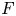$F$ be a totally real field in which 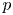$p$ is unramified and let 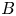$B$ be a quaternion algebra over 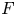$F$ which splits at at most one infinite place. Let $\overline {r}:\operatorname {{\mathrm {Gal}}}(\overline {F}/F)\rightarrow \mathrm {GL}_2(\overline {\mathbb {F}}_p)$ be a modular Galois representation which satisfies the Taylor–Wiles hypotheses. Assume that for some fixed place 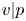$v|p$, 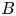$B$ ramifies at 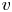$v$ and 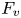$F_v$ is isomorphic to 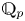$\mathbb {Q}_p$ and 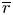$\overline {r}$ is generic at 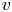$v$. We prove that the admissible smooth representations of the quaternion algebra over 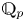$\mathbb {Q}_p$ coming from mod 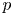$p$ cohomology of Shimura varieties associated to 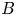$B$ have Gelfand–Kirillov dimension 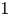$1$. As an application we prove that the degree-two Scholze's functor (which is defined by Scholze [On the 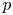$p$-adic cohomology of the Lubin–Tate tower, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 811–863]) vanishes on generic supersingular representations of 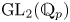$\mathrm {GL}_2(\mathbb {Q}_p)$. We also prove some finer structure theorems about the image of Scholze's functor in the reducible case.

Keywords

mod p Langlands programScholze's functor

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 11 , November 2024 , pp. 2585 - 2655
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barthel, L. and Livné, R., Irreducible modular representations of ${\rm GL_2}$ of a local field, Duke Math. J. 75 (1994), 261–292.CrossRefGoogle Scholar
Breuil, C., Sur quelques représentations modulaires et $p$-adiques de ${\rm GL_2}(\boldsymbol Q_p)$. I, Compos. Math. 138 (2003), 165–188.CrossRefGoogle Scholar
Breuil, C. and Diamond, F., Formes modulaires de Hilbert modulo $p$ et valeurs d'extensions entre caractères galoisiens, Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 905–974.CrossRefGoogle Scholar
Breuil, C., Herzig, F., Hu, Y., Morra, S. and Schraen, B., Conjectures and results on modular representations of ${\rm GL_n}$ of a $p$-adic field $K$, Mem. Amer. Math. Soc., to appear. Preprint (2021), arXiv:2102.06188.Google Scholar
Breuil, C., Herzig, F., Hu, Y., Morra, S. and Schraen, B., Gelfand–Kirillov dimension and mod $p$ cohomology for ${\rm GL}_2$, Invent. Math. 234 (2023), 1–128.CrossRefGoogle Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires et représentations de ${\rm GL_2}(\mathbf{Z}_p)$ et de ${\rm Gal}(\overline {\mathbf{Q}}_p/\mathbf{Q}_p)$ en $l=p$, Duke Math. J. 115 (2002), 205–310, with an appendix by Guy Henniart.CrossRefGoogle Scholar
Breuil, C. and Paškūnas, V., Towards a modulo $p$ Langlands correspondence for ${\rm GL_2}$, Mem. Amer. Math. Soc. 216 (2012).Google Scholar
Brumer, A., Pseudocompact algebras, profinite groups and class formations, J. Algebra 4 (1966), 442–470.CrossRefGoogle Scholar
Bushnell, C. and Henniart, G., The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 335 (Springer, Berlin, 2006).CrossRefGoogle Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre's conjecture for mod $\ell$ Galois representations over totally real fields, Duke Math. J. 155 (2010), 105–161.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the $p$-adic local Langlands correspondence, Camb. J. Math. 4 (2016), 197–287.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the $p$-adic Langlands program for ${\rm GL_2}(\Bbb Q_p)$, Compos. Math. 154 (2018), 503–548.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some $l$-adic lifts of automorphic mod $l$ Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181, with Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.CrossRefGoogle Scholar
Colmez, P., Représentations de ${\rm GL_2}(\boldsymbol Q_p)$ et $(\phi,\Gamma )$-modules, Astérisque 330 (2010), 281–509.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat's last theorem, Elliptic curves, modular forms & Fermat's last theorem (Hong Kong, 1993) (International Press, Cambridge, MA, 1997), 2–140.Google Scholar
Diamond, F., L-functions and Galois representations, in A correspondence between representations of local Galois groups and Lie-type groups, London Mathematical Society Lecture Note series, vol. 320 (Cambridge University Press, Cambridge, 2007), 187–206.Google Scholar
Diamond, F. and Taylor, R., Lifting modular mod $l$ representations, Duke Math. J. 74 (1994), 253–269.CrossRefGoogle Scholar
Dospinescu, G. and Le Bras, A.-C., Revêtements du demi-plan de Drinfeld et correspondance de Langlands $p$-adique, Ann. of Math. (2) 186 (2017), 321–411.CrossRefGoogle Scholar
Dospinescu, G., Paškūnas, V. and Schraen, B., Gelfand–Kirillov dimension and the $p$-adic Jacquet–Langlands correspondence, J. Reine Angew. Math. 801 (2023), 57–114.Google Scholar
Dotto, A. and Le, D., Diagrams in the mod $p$ cohomology of Shimura curves, Compos. Math. 157 (2021), 1653–1723.CrossRefGoogle Scholar
Emerton, M., On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms, Invent. Math. 164 (2006), 1–84.CrossRefGoogle Scholar
Emerton, M., Local–global compatibility in the $p$-adic Langlands programme for $\mathrm {GL}_{2/\mathbb {Q}}$, Preprint (2011), https://www.math.uchicago.edu/~emerton/pdffiles/lg.pdf.Google Scholar
Emerton, M., Gee, T. and Savitt, D., Lattices in the cohomology of Shimura curves, Invent. Math. 200 (2015), 1–96.CrossRefGoogle Scholar
Gee, T. and Geraghty, D., The Breuil–Mézard conjecture for quaternion algebras, Ann. Inst. Fourier (Grenoble) 65 (2015), 1557–1575.CrossRefGoogle Scholar
Gee, T. and Kisin, M., The Breuil–Mézard conjecture for potentially Barsotti–Tate representations, Forum Math. Pi 2 (2014), Paper No. e1.CrossRefGoogle Scholar
Gee, T. and Newton, J., Patching and the completed homology of locally symmetric spaces, J. Inst. Math. Jussieu 21 (2022), 395–458.CrossRefGoogle Scholar
Gee, T. and Savitt, D., Serre weights for quaternion algebras, Compos. Math. 147 (2011), 1059–1086.CrossRefGoogle Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001), with an appendix by Vladimir G. Berkovich.Google Scholar
Henniart, G., Sur l'unicité des types pour ${\rm GL_2}$, appendix to C. Breuil, and A. Mézard: Multiplicités modulaires et représentations de ${\rm GL_2}(\textbf {Z}_p)$ et de ${\rm Gal}(\overline {\textbf {Q}}_p/\textbf {Q}_p)$ en $l=p$, Duke Math. J. 115 (2002), 205–310.Google Scholar
Hu, Y., Multiplicities of cohomological automorphic forms on ${\rm GL_2}$ and mod $p$ representations of ${\rm GL_2}(\Bbb {Q}_p)$, J. Eur. Math. Soc. (JEMS) 23 (2021), 3625–3678.CrossRefGoogle Scholar
Hu, Y. and Paškūnas, V., On crystabelline deformation rings of ${\rm Gal}(\overline {\Bbb Q}_p/\Bbb Q_p)$, with an appendix by Jack Shotton, Math. Ann. 373 (2019), 421–487.CrossRefGoogle Scholar
Hu, Y. and Tan, F., The Breuil–Mézard conjecture for split non-scalar residual representations, Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 1383–1421.CrossRefGoogle Scholar
Hu, Y. and Wang, H., On the $\bmod p$ cohomology for ${\rm GL_2}$: the non-semisimple case, Camb. J. Math. 10 (2022), 261–431.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. E30 (Friedrich Vieweg & Sohn, Braunschweig, 1996).CrossRefGoogle Scholar
Johansson, C., Ludwig, J. and Hansen, D., A quotient of the Lubin–Tate tower II, Math. Ann. 380 (2021), 43–89.CrossRefGoogle Scholar
Khare, C., A local analysis of congruences in the $(p,p)$ case. II, Invent. Math. 143 (2001), 129–155.CrossRefGoogle Scholar
Kisin, M., The Fontaine–Mazur conjecture for ${\rm GL_2}$, J. Amer. Math. Soc. 22 (2009), 641–690.CrossRefGoogle Scholar
Kohlhaase, J., On the Iwasawa theory of the Lubin–Tate moduli space, Compos. Math. 149 (2013), 793–839.CrossRefGoogle Scholar
Lazard, M., Groupes analytiques $p$-adiques, Publ. Math. Inst. Hautes Études Sci. 26 (1965), 389–603.Google Scholar
Ludwig, J., A quotient of the Lubin–Tate tower, Forum Math. Sigma 5 (2017), Paper No. e17.CrossRefGoogle Scholar
Matsumura, H., Commutative ring theory, second edition, Cambridge Studies in Advanced Mathematics, vol. 8 (Cambridge University Press, Cambridge, 1989), translated from the Japanese by M. Reid.Google Scholar
Morra, S., Explicit description of irreducible ${\rm GL_2}(\boldsymbol Q_p)$-representations over $\overline {\boldsymbol F}_p$, J. Algebra 339 (2011), 252–303.CrossRefGoogle Scholar
Morra, S., Sur les atomes automorphes de longueur 2 de $\bf {GL}_2(\bf {Q}_p)$, Doc. Math. 22 (2017), 777–823.CrossRefGoogle Scholar
Newton, J., Completed cohomology of Shimura curves and a $p$-adic Jacquet–Langlands correspondence, Math. Ann. 355 (2013), 729–763.CrossRefGoogle Scholar
Paškūnas, V., Coefficient systems and supersingular representations of ${\rm GL_2}(F)$, Mém. Soc. Math. Fr. (N.S.) 99 (2004).Google Scholar
Paškūnas, V., Extensions for supersingular representations of ${\rm GL_2}(\mathbb { Q}_p)$, Astérisque 331 (2010), 317–353.Google Scholar
Paškūnas, V., The image of Colmez's Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191.CrossRefGoogle Scholar
Paškūnas, V., On the Breuil-Mézard conjecture, Duke Math. J. 164 (2015), 297–359.CrossRefGoogle Scholar
Paškūnas, V., On some consequences of a theorem of J. Ludwig, J. Inst. Math. Jussieu 21 (2022), 1067–1106.CrossRefGoogle Scholar
Sander, F., A local proof of the Breuil–Mézard conjecture in the scalar semi-simplification case, J. Lond. Math. Soc. (2) 94 (2016), 447–461.CrossRefGoogle Scholar
Schneider, P., p-adic Lie groups, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 344 (Springer, Heidelberg, 2011).CrossRefGoogle Scholar
Schneider, P., Teitelbaum, J. and Prasad, D., $U(\mathfrak { g})$-finite locally analytic representations, Represent. Theory 5 (2001), 111–128, with an appendix by Dipendra Prasad.CrossRefGoogle Scholar
Scholze, P., On the $p$-adic cohomology of the Lubin–Tate tower, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 811–863, with an appendix by Michael Rapoport.CrossRefGoogle Scholar
Schraen, B., Sur la présentation des représentations supersingulières de ${\rm GL_2}(F)$, J. Reine Angew. Math. 704 (2015), 187–208.CrossRefGoogle Scholar
Serre, J.-P., Galois cohomology, english edition, Springer Monographs in Mathematics (Springer, Berlin, 2002), translated from the French by Patrick Ion and revised by the author.Google Scholar
Venjakob, O., On the structure theory of the Iwasawa algebra of a $p$-adic Lie group, J. Eur. Math. Soc. (JEMS) 4 (2002), 271–311.CrossRefGoogle Scholar