Hostname: page-component-6bf8c574d5-j5c6p Total loading time: 0 Render date: 2025-03-11T17:40:42.640Z Has data issue: false hasContentIssue false
  • English
  • Français

A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells

Part of: Cycles and subschemes Projective and enumerative geometry Special varieties Singularities (Co)homology theory

Published online by Cambridge University Press:  10 March 2025

Jörg Schürmann ,
Connor Simpson  and
Botong Wang
Jörg Schürmann
Affiliation:
Mathematisches Institut, Universität Münster, Einsteinstr. 62, 48149 Münster, Germany [email protected]
Connor Simpson
Affiliation:
Institute for Advanced Study, 1 Einstein Dr, Princeton, NJ 08540, USA [email protected]
Botong Wang
Affiliation:
Institute for Advanced Study, 1 Einstein Dr, Princeton, NJ 08540 [email protected] Department of Mathematics, University of Wisconsin-Madison, 480 Lincoln Drive, Madison, WI 53706-1388, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove a new generic vanishing theorem for 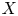$X$ a complete homogeneous variety with respect to an action of a connected algebraic group. Let 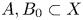$A, B_0\subset X$ be locally closed affine subvarieties, and assume that 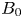$B_0$ is smooth and pure dimensional. Let 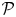${\mathcal {P}}$ be a perverse sheaf on 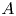$A$ and let 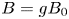$B=g B_0$ be a generic translate of 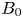$B_0$. Then our theorem implies 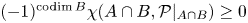$(-1)^{\operatorname {codim} B}\chi (A\cap B, {\mathcal {P}}|_{A\cap B})\geq 0$. As an application, we prove in full generality a positivity conjecture about the signed Euler characteristic of generic triple intersections of Schubert cells. Such Euler characteristics are known to be the structure constants for the multiplication of the Segre–Schwartz–MacPherson classes of these Schubert cells.

Keywords

vanishing theoremperverse sheaveshomogeneous varietyabelian varietyflag varietySchubert cellChern–Schwartz–MacPherson classSegre–Schwartz–MacPherson classEuler characteristictriple intersectionpositivity conjecture

MSC classification

Primary: 14C17: Intersection theory, characteristic classes, intersection multiplicities 14F17: Vanishing theorems 14M15: Grassmannians, Schubert varieties, flag manifolds 14M17: Homogeneous spaces and generalizations
Secondary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 14F45: Topological properties 14N15: Classical problems, Schubert calculus 32S20: Global theory of singularities; cohomological properties 32S60: Stratifications; constructible sheaves; intersection cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 161 , Issue 1 , January 2025 , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2025. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aluffi, P., Mihalcea, L. C., Schürmann, J. and Su, C., Positivity of Segre–MacPherson classes, in Facets of algebraic geometry. Vol. I, London Mathematical Society Lecture Note Series, vol. 472 (Cambridge University Press, Cambridge, 2022), 1–28.Google Scholar
Aluffi, P., Mihalcea, L. C., Schürmann, J. and Su, C., From motivic Chern classes of Schubert cells to their Hirzebruch and CSM classes, in A glimpse into geometric representation theory, Contemporary Mathematics, vol. 804 (American Mathematical Society, Providence, RI, 2024), 1–52.CrossRefGoogle Scholar
Aluffi, P., Mihalcea, L. C., Schürmann, J. and Su, C., Shadows of characteristic cycles, Verma modules, and positivity of Chern–Schwartz–MacPherson classes of Schubert cells, Duke Math. J. 172 (2023), 3257–3320.CrossRefGoogle Scholar
Beilinson, A., On the derived category of perverse sheaves, in K-theory, arithmetic and geometry (Moscow, 1984–1986), Lecture Notes in Mathematics, vol. 1289 (Springer, Berlin, 1987), 27–41.Google Scholar
Billey, S. and Coskun, I., Singularities of generalized Richardson varieties, Comm. Algebra 40 (2012), 1466–1495.CrossRefGoogle Scholar
Brion, M., Spherical varieties, in Highlights in Lie algebraic methods, Progress in Mathematics, vol. 295 (Birkhäuser, New York, 2012), 3–24.CrossRefGoogle Scholar
de Cataldo, M. and Migliorini, L., The perverse filtration and the Lefschetz hyperplane theorem, Ann. of Math. (2) 171 (2010), 2089–2113.CrossRefGoogle Scholar
Dimca, A., Sheaves in topology, Universitext (Springer, Berlin, 2004).CrossRefGoogle Scholar
Fan, N., Guo, P. and Xiong, R., Pieri and Murnaghan–Nakayama type rules for Chern classes of Schubert cells, Preprint (2022), arXiv:2211.06802.Google Scholar
Franecki, J. and Kapranov, M., The Gauss map and a noncompact Riemann–Roch formula for constructible sheaves on semiabelian varieties, Duke Math. J. 104 (2000), 171–180.CrossRefGoogle Scholar
Gabber, O. and Loeser, F., Faisceaux pervers l-adiques sur un tore, Duke Math. J. 83 (1996), 501–606.CrossRefGoogle Scholar
Green, M. and Lazarsfeld, R., Deformation theory, generic vanishing theorems, and some conjectures of Enriques, Catanese and Beauville, Invent. Math. 90 (1987), 389–407.CrossRefGoogle Scholar
Huh, J., The maximum likelihood degree of a very affine variety, Compos. Math. 149 (2013), 1245–1266.CrossRefGoogle Scholar
Kleiman, S., The transversality of a general translate, Compos. Math. 28 (1974), 287–297.Google Scholar
Knutson, A. and Zinn-Justin, P., Schubert puzzles and integrability II: Multiplying motivic Segre classes, Preprint (2021), arXiv:2102.00563.Google Scholar
Knutson, A., Schubert calculus and quiver varieties, in International Congress of Mathematics, vol. 6 (EMS Press, Berlin, Germany, 2023), 4582–4605.CrossRefGoogle Scholar
Kumar, S., Conjectural positivity of Chern–Schwartz–MacPherson classes for Richardson cells, Int. Math. Res. Not. IMRN 2024 (2024), 1154–1165.CrossRefGoogle Scholar
Liu, Y., Maxim, L. and Wang, B., Generic vanishing for semi-abelian varieties and integral Alexander modules, Math. Z. 293 (2019), 629–645.CrossRefGoogle Scholar
Liu, Y., Maxim, L. and Wang, B., Topology of subvarieties of complex semi-abelian varieties, Int. Math. Res. Not. IMRN 2021 (2021), 11169–11208.CrossRefGoogle Scholar
Maxim, L. and Schürmann, J., Constructible sheaf complexes in complex geometry and applications, in Handbook of geometry and topology of singularities III (Springer, Cham, 2022), 679–791.CrossRefGoogle Scholar
Richardson, R. W., Intersections of double cosets in algebraic groups, Indag. Math. (N.S.) 3 (1992), 69–77.CrossRefGoogle Scholar
Rodriguez, J. I. and Wang, B., The maximum likelihood degree of mixtures of independence models, SIAM J. Appl. Algebra Geom. 1 (2017), 484–506.CrossRefGoogle Scholar
Schnell, C., Holonomic D-modules on abelian varieties, Publ. Math. Inst. Hautes Études Sci. 121 (2015), 1–55.CrossRefGoogle Scholar
Schürmann, J., Topology of singular spaces and constructible sheaves, Monografie Matematyczne (New Series), vol. 63 (Birkhäuser, Basel, 2003).CrossRefGoogle Scholar
Schürmann, J., Chern classes and transversality for singular spaces, in Singularities in geometry, topology, foliations and dynamics, Trends in Mathematics (Birkhäuser, Basel, 2017), 207–231.CrossRefGoogle Scholar
Schürmann, J. and Tibăr, M., Index formula for MacPherson cycles of affine algebraic varieties, Tohoku Math. J. 62 (2010), 29–44.CrossRefGoogle Scholar
Seade, J., Tibăr, M. and Verjovsky, A., Global Euler obstruction and polar invariants, Math. Ann. 333 (2005), 393–403.CrossRefGoogle Scholar
Su, C., Structure constants for Chern classes of Schubert cells, Math. Z. 298 (2021), 193–213.CrossRefGoogle Scholar