Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-28T09:55:52.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Low-degree Hurwitz stacks in the Grothendieck ring

Part of: Families, fibrations Birational geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  11 September 2024

Aaron Landesman Open the ORCID record for Aaron Landesman [Opens in a new window] ,
Ravi Vakil Open the ORCID record for Ravi Vakil [Opens in a new window]  and
Melanie Matchett Wood Open the ORCID record for Melanie Matchett Wood [Opens in a new window]
Aaron Landesman
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA 02138, USA [email protected]
Ravi Vakil
Affiliation:
Department of Mathematics, Stanford University, 450 Jane Stanford Way, Stanford, CA 94305, USA [email protected]
Melanie Matchett Wood
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA 02138, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 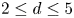$2 \leq d \leq 5$, we show that the class of the Hurwitz space of smooth degree $d$, genus 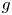$g$ covers of 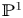$\mathbb {P}^1$ stabilizes in the Grothendieck ring of stacks as 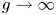$g \to \infty$, and we give a formula for the limit. We also verify this stabilization when one imposes ramification conditions on the covers, and obtain a particularly simple answer for this limit when one restricts to simply branched covers.

Keywords

motivic statisticsGrothendieck ringHurwitz spacesCasnati--Ekedahl parameterizations

MSC classification

Primary: 14G99: None of the above, but in this section
Secondary: 14D23: Stacks and moduli problems 14E20: Coverings
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 8 , August 2024 , pp. 1784 - 1849
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

With an appendix by Aaron Landesman and Federico Scavia

References

Ali Altug, S., Shankar, A., Varma, I. and Wilson, K. H., The number of $D_4$-fields ordered by conductor, J. Eur. Math. Soc. (JEMS) 23 (2021), 2733–2785.CrossRefGoogle Scholar
Aoki, M., Hom stacks, Manuscripta Math. 119 (2006), 37–56.CrossRefGoogle Scholar
Aoki, M., Erratum: ‘Hom stacks’ [Manuscripta Math. 119 (2006), no. 1, 37–56; MR2194377], Manuscripta Math. 121 (2006), 135.CrossRefGoogle Scholar
Arsie, A. and Vistoli, A., Stacks of cyclic covers of projective spaces, Compos. Math. 140 (2004), 647–666.CrossRefGoogle Scholar
Behrend, K. and Dhillon, A., On the motivic class of the stack of bundles, Adv. Math. 212 (2007), 617–644.CrossRefGoogle Scholar
Behrend, K. A., The Lefschetz trace formula for the moduli stack of principal bundles, PhD thesis, University of California, Berkeley (ProQuest LLC, Ann Arbor, MI, 1991).Google Scholar
Bertin, J. and Romagny, M., Champs de Hurwitz, Mém. Soc. Math. Fr. (N.S.) 125–126 (2011), 219.Google Scholar
Bhargava, M., Higher composition laws III: The parametrization of quartic rings, Ann. Math. 159 (2004), 1329–1360.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quartic rings and fields, Ann. Math. 162 (2005), 1031–1063.CrossRefGoogle Scholar
Bhargava, M., Mass formulae for extensions of local fields, and conjectures on the density of number field discriminants, Int. Math. Res. Not. IMRN 2007 (2007), rnm052.CrossRefGoogle Scholar
Bhargava, M., Higher composition laws. IV. The parametrization of quintic rings, Ann. of Math. (2) 167 (2008), 53–94.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quintic rings and fields, Ann. Math. 172 (2010), 1559–1591.CrossRefGoogle Scholar
Bhargava, M., The geometric sieve and the density of squarefree values of invariant polynomials, Preprint (2014), arXiv:1402.0031v1.Google Scholar
Bhargava, M., Shankar, A. and Tsimerman, J., On the Davenport–Heilbronn theorems and second order terms, Invent. Math. 193 (2013), 439–499.CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Wang, X., Geometry-of-numbers methods over global fields I: Prehomogeneous vector spaces, Preprint (2015), arXiv:1512.03035v1.Google Scholar
Bhargava, M., Taniguchi, T. and Thorne, F., Improved error estimates for the Davenport–Heilbronn theorems, Preprint (2021), arXiv:2107.12819.Google Scholar
Bilu, M., Produits eulériens motiviques, PhD thesis, Université Paris-Saclay (ComUE) (2017).Google Scholar
Bilu, M., Das, R. and Howe, S., Zeta statistics and Hadamard functions, Adv. Math. 407 (2022), 108556.CrossRefGoogle Scholar
Bilu, M. and Howe, S., Motivic Euler products in motivic statistics, Algebra Number Theory 15 (2021), 2195–2259.CrossRefGoogle Scholar
Bolognesi, M. and Vistoli, A., Stacks of trigonal curves, Trans. Amer. Math. Soc. 364 (2012), 3365–3393.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Buchsbaum, D. A. and Eisenbud, D., Algebra structures for finite free resolutions, and some structure theorems for ideals of codimension $3$, Amer. J. Math. 99 (1977), 447–485.CrossRefGoogle Scholar
Canning, S. and Larson, H., Chow rings of low-degree Hurwitz spaces, J. Reine Angew. Math. 789 (2022), 103–152.CrossRefGoogle Scholar
Canning, S. and Larson, H., Tautological classes on low-degree Hurwitz spaces, Int. Math. Res. Not. IMRN 2024 (2024), rnac360.CrossRefGoogle Scholar
Casnati, G., Covers of algebraic varieties II. Covers of degree 5 and construction of surfaces, J. Algebraic Geom. 5 (1996), 461–478.Google Scholar
Casnati, G. and Ekedahl, T., Covers of algebraic varieties I. A general structure theorem, covers of degree 3, 4 and Enriques surfaces, J. Algebraic Geom. 5 (1996), 439–460.Google Scholar
Casnati, G. and Notari, R., On some Gorenstein loci in $Hilb_6(\Bbb P^4_k)$, J. Algebra 308 (2007), 493–523.CrossRefGoogle Scholar
Cohen, H., Diaz y Diaz, F. and Olivier, M., Enumerating quartic dihedral extensions of $\mathbb {Q}$, Compos. Math. 133 (2002), 65–93.CrossRefGoogle Scholar
Conrad, B., Grothendieck duality and base change, Lecture Notes in Mathematics, vol. 1750 (Springer, Berlin, 2000).CrossRefGoogle Scholar
Datskovsky, B. and Wright, D. J., Density of discriminants of cubic extensions, J. Reine Angew. Math. 386 (1988), 116–138.Google Scholar
Davenport, H. and Heilbronn, H., On the density of discriminants of cubic fields, Bull. Lond. Math. Soc. 1 (1969), 345–348.CrossRefGoogle Scholar
Davenport, H. and Heilbronn, H., On the density of discriminants of cubic fields. II, Proc. Roy. Soc. Lond. Ser. A. Math. Phys. Eng. Sci. 322 (1971), 405–420.Google Scholar
Delone, B. N. and Faddeev, D. K., The theory of irrationalities of the third degree, Translations of Mathematical Monographs, vol. 10 (American Mathematical Society, Providence, RI, 1964).Google Scholar
Deopurkar, A., Compactifications of Hurwitz spaces, Int. Math. Res. Not. IMRN 2014 (2014), 3863–3911.CrossRefGoogle Scholar
Deopurkar, A. and Patel, A., The Picard rank conjecture for the Hurwitz spaces of degree up to five, Algebra Number Theory 9 (2015), 459–492.CrossRefGoogle Scholar
Eisenbud, D., Commutative algebra: With a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995).CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., 3264 and all that—a second course in algebraic geometry (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Ekedahl, T., The Grothendieck group of algebraic stacks, Preprint (2009), arXiv:0903.3143v2.Google Scholar
Ekedahl, T., A geometric invariant of a finite group, Preprint (2009), arXiv:0903.3148v1.Google Scholar
Ellenberg, J. S., Venkatesh, A. and Westerland, C., Homological stability for Hurwitz spaces and the Cohen-Lenstra conjecture over function fields, Ann. of Math. (2) 183 (2016), 729–786.CrossRefGoogle Scholar
Fantechi, B., Göttsche, L., Illusie, L., Kleiman, S. L., Nitsure, N. and Vistoli, A., Fundamental algebraic geometry: Grothendieck's FGA explained, Mathematical Surveys and Monographs, vol. 123 (American Mathematical Society, Providence, RI, 2005),Google Scholar
Fantechi, B. and Pandharipande, R., Stable maps and branch divisors, Compos. Math. 130 (2002), 345–364.CrossRefGoogle Scholar
Fulton, W., Hurwitz schemes and irreducibility of moduli of algebraic curves, Ann. Math. 90 (1969), 542–575.CrossRefGoogle Scholar
Gaitsgory, D. and Lurie, J., Weil's conjecture for function fields. Vol. 1, Annals of Mathematics Studies, vol. 199 (Princeton University Press, Princeton, NJ, 2019).Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. 24 (231), 1965.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. 28 (255), 1966.Google Scholar
Grothendieck, A., Le groupe de Brauer. III. Exemples et compléments, in Dix exposés sur la cohomologie des schémas, Advanced Studies in Pure Mathematics, vol. 3 (North-Holland, Amsterdam, 1968), 88–188.Google Scholar
Gusein-Zade, S. M., Luengo, I. and Melle-Hernàndez, A., A power structure over the Grothendieck ring of varieties, Math. Res. Lett. 11 (2004), 49–57.CrossRefGoogle Scholar
Hatcher, A., A short exposition of the Madsen-Weiss theorem, Preprint (2011), arXiv:1103.5223.Google Scholar
Larson, H. K., The intersection theory of the moduli stack of vector bundles on $\mathbb {P}^1$, Canad. Math. Bull. (2021), 1–21.Google Scholar
Madsen, I. and Weiss, M., The stable moduli space of Riemann surfaces: Mumford's conjecture, Ann. of Math. (2) 165 (2007), 843–941.CrossRefGoogle Scholar
Miranda, R., Triple covers in algebraic geometry, Amer. J. Math. 107 (1985), 1123–1158.CrossRefGoogle Scholar
Olsson, M., Algebraic spaces and stacks, AMS Colloquium Publications, vol. 62 (American Mathematical Society, Providence, RI, 2016).Google Scholar
Pardini, R., Triple covers in positive characteristic, Ark. Mat. 27 (1989), 319–341.CrossRefGoogle Scholar
Patel, A. P., The geometry of Hurwitz space, PhD thesis, Harvard University (2013).Google Scholar
Roberts, D., Density of cubic field discriminants, Math. Comput. 70 (2001), 1699–1705.CrossRefGoogle Scholar
Poonen, B., The moduli space of commutative algebras of finite rank, J. Eur. Math. Soc. (JEMS) (2008), 817–836.CrossRefGoogle Scholar
Rydh, D., Étale dévissage, descent and pushouts of stacks, J. Algebra 331 (2011), 194–223.CrossRefGoogle Scholar
Schreyer, F.-O., Syzygies of canonical curves and special linear series, Math. Ann. 275 (1986), 105–137.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu.Google Scholar
Taniguchi, T. and Thorne, F., Secondary terms in counting functions for cubic fields, Duke Math. J. 162 (2013), 2451–2508.CrossRefGoogle Scholar
Vakil, R. and Wood, M. M., Discriminants in the Grothendieck ring, Duke Math. J. 164 (2015), 1139–1185.CrossRefGoogle Scholar
Wewers, S., Construction of Hurwitz spaces, Dissertation, Universität Essen (IEM, 1998).Google Scholar
Wood, M. M., Parametrizing quartic algebras over an arbitrary base, Algebra Number Theory 5 (2011), 1069–1094.CrossRefGoogle Scholar
Wood, M. M., Asymptotics for number fields and class groups, in Directions in number theory, Association for Women in Mathematics Series, vol. 3 (Springer, Cham, 2016), 291–339.CrossRefGoogle Scholar
Wright, D. J. and Yukie, A., Prehomogeneous vector spaces and field extensions, Invent. Math. 110 (1992), 283–314.CrossRefGoogle Scholar
Zhao, Y., On sieve methods for varieties over finite fields, PhD thesis, The University of Wisconsin–Madison (ProQuest LLC, Ann Arbor, MI, 2013).Google Scholar
Zheng, A., Stable cohomology of the moduli space of trigonal curves, Int. Math. Res. Not. IMRN 2024 (2024), rnad011.CrossRefGoogle Scholar