Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-29T03:03:51.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Haagerup and Størmer's conjecture on pointwise inner automorphisms

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  04 November 2024

Yusuke Isono
Yusuke Isono*
Affiliation:
Research Institute for Mathematical Sciences (RIMS), Kyoto University, 606-8502 Kyoto, Japan [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1988, Haagerup and Størmer conjectured that every pointwise inner automorphism of a type 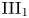${\rm III_1}$ factor is a composition of an inner and a modular automorphism. We study this conjecture and prove that every type 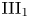${\rm III_1}$ factor with trivial bicentralizer indeed satisfies this condition. In particular, this shows that Haagerup and Størmer's conjecture holds in full generality if Connes’ bicentralizer problem has an affirmative answer. Our proof is based on Popa's intertwining theory and Marrakchi's recent work on relative bicentralizers.

Keywords

pointwise inner automorphismstype III factorsTomita–Takesaki theory

MSC classification

Primary: 46L10: General theory of von Neumann algebras 46L36: Classification of factors 46L40: Automorphisms
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 10 , October 2024 , pp. 2480 - 2495
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ando, H. and Haagerup, U., Ultraproducts of von Neumann algebras, J. Funct. Anal. 266 (2014), 6842–6913.CrossRefGoogle Scholar
Ando, H., Haagerup, U., Houdayer, C. and Marrakchi, A., Structure of bicentralizer algebras and inclusions of type ${\rm III}$ factors, Math. Ann. 376 (2020), 1145–1194.CrossRefGoogle Scholar
Connes, A., Une classification des facteurs de type ${\rm III}$, Ann. Sci. Éc. Norm. Super. (4) 6 (1973), 133–252.CrossRefGoogle Scholar
Haagerup, U., Connes’ bicentralizer problem and uniqueness of the injective factor of type ${\rm III_1}$, Acta Math. 158 (1987), 95–148.CrossRefGoogle Scholar
Haagerup, U. and Størmer, E., Equivalence of normal states on von Neumann algebras and the flow of weights, Adv. Math. 83 (1990), 180–262.CrossRefGoogle Scholar
Haagerup, U. and Størmer, E., Pointwise inner automorphisms of von Neumann algebras, J. Funct. Anal. 92 (1990), 177–201, with an appendix by Colin Sutherland.CrossRefGoogle Scholar
Haagerup, U. and Størmer, E., Pointwise inner automorphisms of injective factors, J. Funct. Anal. 122 (1994), 307–314.CrossRefGoogle Scholar
Houdayer, C. and Isono, Y., Unique prime factorization and bicentralizer problem for a class of type ${\rm III}$ factors, Adv. Math. 305 (2017), 402–455.CrossRefGoogle Scholar
Houdayer, C. and Isono, Y., Pointwise inner automorphisms of almost periodic factors, Selecta Math. (N.S.) 30 (2024), paper 58.CrossRefGoogle Scholar
Houdayer, C. and Popa, S., Singular MASAs in type III factors and Connes’ bicentralizer property, in Operator algebras and mathematical physics, Advanced Studies in Pure Mathematics, vol. 80 (Mathematical Society of Japan, Tokyo, 2019), 109–122.CrossRefGoogle Scholar
Houdayer, C. and Vaes, S., Type ${\rm III}$ factors with unique Cartan decomposition, J. Math. Pures Appl. (9) 100 (2013), 564–590.CrossRefGoogle Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. II. Advanced theory, Graduate Studies in Mathematics, vol. 16 (American Mathematical Society, Providence, RI, 1997). Corrected reprint of the 1986 original.Google Scholar
Kawahigashi, Y., Sutherland, C. E. and Takesaki, M., The structure of the automorphism group of an injective factor and the cocycle conjugacy of discrete abelian group actions, Acta Math. 169 (1992), 105–130.CrossRefGoogle Scholar
Marrakchi, A., Full factors, bicentralizer flow and approximately inner automorphisms, Invent. Math. 222 (2020), 375–398.CrossRefGoogle Scholar
Marrakchi, A., Kadison's problem for type ${\rm III}$ subfactors and the bicentralizer conjecture, Preprint (2023), arXiv:2308.15163Google Scholar
Ocneanu, A., Actions of discrete amenable groups on von Neumann algebras, Lecture Notes in Mathematics, vol. 1138 (Springer, Berlin, 1985).CrossRefGoogle Scholar
Popa, S., On a problem of R.V. Kadison on maximal abelian $\ast$-subalgebras in factors, Invent. Math. 65 (1981), 269–281.CrossRefGoogle Scholar
Popa, S., Singular maximal abelian $\ast$-subalgebras in continuous von Neumann algebras, J. Funct. Anal. 50 (1983), 151–166.CrossRefGoogle Scholar
Popa, S., Classification of subfactors and their endomorphisms, CBMS Regional Conference Series in Mathematics, vol. 86 (American Mathematical Society, Providence, RI, 1995).CrossRefGoogle Scholar
Popa, S., On a class of type ${\rm II_1}$ factors with Betti numbers invariants, Ann. of Math. (2) 163 (2006), 809–899.CrossRefGoogle Scholar
Popa, S., Strong rigidity of ${\rm II_1}$ factors arising from malleable actions of w-rigid groups ${\rm I}$, Invent. Math. 165 (2006), 369–408.CrossRefGoogle Scholar
Popa, S., Constructing MASAs with prescribed properties, Kyoto J. Math. 59 (2019), 367–397.CrossRefGoogle Scholar
Takesaki, M., Theory of operator algebras II, Encyclopedia of Mathematical Sciences, vol. 125; Operator algebras and non-commutative geometry, vol. VI (Springer, Berlin, 2003).CrossRefGoogle Scholar