Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-27T13:52:27.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles

Part of: Surfaces and higher-dimensional varieties Cycles and subschemes

Published online by Cambridge University Press:  18 December 2023

François Charles ,
Giovanni Mongardi  and
Gianluca Pacienza
François Charles
Affiliation:
DMA – École normale superiéure, 45 rue d'Ulm, 75230 Paris Cedex 05, France [email protected]
Giovanni Mongardi
Affiliation:
Dipartimento di Matematica, Alma Mater studiorum Universitá di Bologna, Piazza di Porta San Donato 5, Bologna 40126, Italy [email protected]
Gianluca Pacienza
Affiliation:
Université de Lorraine, CNRS, IECL, F-54000 Nancy, France [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study families of rational curves on irreducible holomorphic symplectic varieties. We give a necessary and sufficient condition for a sufficiently ample linear system on a holomorphic symplectic variety of 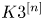$K3^{[n]}$-type to contain a uniruled divisor covered by rational curves of primitive class. In particular, for any fixed 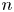$n$, we show that there are only finitely many polarization types of holomorphic symplectic variety of 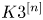$K3^{[n]}$-type that do not contain such a uniruled divisor. As an application, we provide a generalization of a result due to Beauville–Voisin on the Chow group of 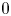$0$-cycles on such varieties.

Keywords

rational curvesirreducible symplectic varietiesChow groups

MSC classification

Primary: 14C99: None of the above, but in this section 14J28: $K3$ surfaces and Enriques surfaces
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 2 , February 2024 , pp. 288 - 316
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramovich, D. and Vistoli, A., Compactifying the space of stable maps, J. Amer. Math. Soc. 15 (2002), 27–75.CrossRefGoogle Scholar
Amerik, E. and Verbitsky, M., Rational curves on hyperkähler manifolds, Int. Math. Res. Not. IMRN 2015 (2015), 13009–13045.Google Scholar
Apostolov, A., Moduli spaces of polarized irreducible symplectic manifolds are not necessarily connected, Ann. Inst. Fourier 64 (2014), 189–202.CrossRefGoogle Scholar
Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A., Compact complex surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 4, second edition (Springer, Berlin, 2004).Google Scholar
Beauville, A., Variétés Kähleriennes dont la première classe de Chern est nulle, J. Differential Geom. 18 (1983), 755–782.CrossRefGoogle Scholar
Beauville, A., On the splitting of the Bloch–Beilinson filtration, in Algebraic cycles and motives, Vol. 2, London Mathematical Society Lecture Note Series, vol. 344 (Cambridge Univeristy Press, Cambridge, 2007), 38–53.Google Scholar
Beauville, A. and Voisin, C., On the Chow ring of a $K3$ surface, J. Algebraic Geom. 13 (2004), 417–426.CrossRefGoogle Scholar
Behrend, K. and Manin, Y., Stacks of stable maps and Gromov–Witten invariants, Duke Math. J. 85 (1996), 1–60.CrossRefGoogle Scholar
Bogomolov, F., Hassett, B. and Tschinkel, Y., Constructing rational curves on K3 surfaces, Duke Math. J. 157 (2011), 535–550.CrossRefGoogle Scholar
Charles, F. and Pacienza, G., Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles, Preprint (2014), arXiv:1401.4071v2.Google Scholar
Chen, X., A simple proof that rational curves on $K3$ are nodal, Math. Ann. 324 (2002), 71–104.CrossRefGoogle Scholar
Chiantini, L. and Sernesi, E., Nodal curves on surfaces of general type, Math. Ann. 307 (1997), 41–56.CrossRefGoogle Scholar
Ciliberto, C. and Knutsen, A. L., On $k$-gonal loci in Severi varieties on general $K3$ surfaces and rational curves on hyperkähler manifolds, J. Math. Pures Appl. (9) 101 (2014), 473–494.CrossRefGoogle Scholar
Ferretti, A., Special subvarieties of EPW sextics, Math. Z. 272 (2012), 1137–1164.CrossRefGoogle Scholar
Fogarty, J., Algebraic families on an algebraic surface, Amer. J. Math. 90 (1968), 511–521.CrossRefGoogle Scholar
Fu, L., Decomposition of small diagonals and Chow rings of hypersurfaces and Calabi–Yau complete intersections, Adv. Math. 244 (2013), 894–924.CrossRefGoogle Scholar
Fu, L., Beauville–Voisin conjecture for generalized Kummer varieties, Int. Math. Res. Not. IMRN 2015 (2015), 3878–3898.Google Scholar
Fu, L., Laterveer, R., Vial, C. and Shen, M., The generalized Franchetta conjecture for some hyper-Kähler varieties, J. Math. Pures Appl. 130 (2019), 1–35.CrossRefGoogle Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 2, second edition (Springer, Berlin, 1998).Google Scholar
Fulton, W. and Pandharipande, R., Notes on stable maps and quantum cohomology, in Algebraic geometry—Santa Cruz 1995, Proceedings of Symposia in Pure Mathematics, vol. 62 (American Mathematical Society, Providence, RI, 1997), 45–96.Google Scholar
Galati, C. and Knutsen, A. L., On the existence of curves with $a_k$-singularities on $K3$-surfaces, Math. Res. Lett. 21 (2014), 1069–1109.CrossRefGoogle Scholar
Gritsenko, V., Hulek, K. and Sankaran, G. K., Moduli spaces of irreducible symplectic manifolds, Compos. Math. 146 (2010), 404–434.CrossRefGoogle Scholar
Hassett, B. and Tschinkel, Y., Intersection numbers of extremal rays on holomorphic symplectic varieties, Asian J. Math. 14 (2010), 303–322.CrossRefGoogle Scholar
Huybrechts, D., Compact hyper-Kähler manifolds: basic results, Invent. Math. 135 (1999), 63–113.CrossRefGoogle Scholar
Huybrechts, D., Curves and cycles on K3 surfaces, Algebr. Geom. 1 (2014), 69–106.CrossRefGoogle Scholar
Klemm, A., Maulik, D., Pandharipande, R. and Scheidegger, E., Noether–Lefschetz theory and the Yau–Zaslow conjecture, J. Amer. Math. Soc. 23 (2010), 1013–1040.CrossRefGoogle Scholar
Knutsen, A., Lelli-Chiesa, M. and Mongardi, G., Wall divisors and algebraically coisotropic subvarieties of irreducible holomorphic symplectic manifolds, Trans. Am. Math. Soc. 371 (2019), 1403–1438.CrossRefGoogle Scholar
Kreck, M. and Su, Y., Finiteness and infiniteness results for Torelli groups of (hyper-)Kähler manifolds, Math. Ann. 381 (2021), 841–852.Google Scholar
Laterveer, R., A remark on Beauville's splitting property, Manuscripta Math. 156 (2018), 117–125.CrossRefGoogle Scholar
Lehn, C. and Pacienza, G., Stability of coisotropic fibrations on holomorphic symplectic manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XIX (2019), 965–980.Google Scholar
Lin, H.-Y., On the Chow group of zero-cycles of a generalized Kummer variety, Adv. Math. (NY) 298 (2016), 448–472.CrossRefGoogle Scholar
Lin, H.-Y., Lagrangian constant cycle subvarieties in Lagrangian fibrations, Int. Math. Res. Not. IMRN 2020 (2020), 14–24.CrossRefGoogle Scholar
Looijenga, E., Teichmüller spaces and Torelli theorems for hyperkähler manifolds, Math. Z. 298 (2021), 261–279.CrossRefGoogle Scholar
Markman, E., Integral constraints on the monodromy group of the hyperKähler resolution of a symmetric product of a $K3$ surface, Internat. J. Math. 21 (2010), 169–223.CrossRefGoogle Scholar
Markman, E., A survey of Torelli and monodromy results for holomorphic-symplectic varieties, in Complex and differential geometry, Springer Proceedings in Mathematics (2011), 257–322.Google Scholar
Mongardi, G. and Ottem, J. C., Curve classes on irreducible holomorphic symplectic varieties, Commun. Contemp. Math. 22 (2020), 1950078.CrossRefGoogle Scholar
Mongardi, G. and Pacienza, G., Polarized parallel transport and uniruled divisors on deformations of generalized Kummer varieties, Int. Math. Res. Not. IMRN 2018 (2018), 3606–3620.CrossRefGoogle Scholar
Mongardi, G. and Pacienza, G., Corrigendum and addendum to “Polarized parallel transport and uniruled divisors on deformations of generalized Kummer varieties”, Int. Math. Res. Not. IMRN 2021 (2021), 14398–14404.Google Scholar
Mori, S. and Mukai, S., The uniruledness of the moduli space of curves of genus 11, in Algebraic geometry (Tokyo/Kyoto, 1982), Lecture Notes in Mathematics, vol. 1016 (Springer, Berlin, 1983), 334–353.Google Scholar
Nikulin, V. V., Integer symmetric bilinear forms and some of their geometric applications, Izv. Akad. Nauk SSSR Ser. Mat. 43 (1979), 111–177.Google Scholar
Oberdieck, G., Shen, J. and Yin, Q., Rational curves in holomorphic symplectic varieties and Gromov–Witten invariants, Adv. Math. 357 (2019), 106829.CrossRefGoogle Scholar
Ran, Z., Hodge theory and deformation of maps, Compos. Math. 97 (1995), 309–328.Google Scholar
Riess, U., On the Beauville conjecture, Int. Math. Res. Not. IMRN 2016 (2016), 6133–6150.CrossRefGoogle Scholar
Sernesi, E., Deformations of algebraic schemes, Grundlehren der mathematischen Wissenschaften, vol. 334 (Springer, 2006).Google Scholar
Shen, M. and Vial, C., The Fourier transform for certain hyperKähler fourfolds, Mem. Amer. Math. Soc. 240 (2016).CrossRefGoogle Scholar
Shen, J. and Yin, Q., $K3$ categories, one-cycles on cubic fourfolds, and the Beauville–Voisin filtration, J. Inst. Math. Jussieu 19 (2020), 1601–1627.CrossRefGoogle Scholar
Shen, J., Yin, Q. and Zhao, X., Derived categories of K3 surfaces, O'Grady's filtration, and zero-cycles on holomorphic symplectic varieties, Compos. Math. 156 (2020), 179–197.CrossRefGoogle Scholar
Verbitsky, M., Mapping class group and a global Torelli theorem for hyperkähler manifolds, Duke Math. J. 162 (2013), 2929–2986. Appendix A by Eyal Markman.CrossRefGoogle Scholar
Verbitsky, M., Ergodic complex structures on hyperkähler manifolds, Acta Math. 215 (2015), 161–182.CrossRefGoogle Scholar
Verbitsky, M., Ergodic complex structures on hyperkahler manifolds: an erratum, Preprint (2017), arXiv:1708.05802.Google Scholar
Verbitsky, M., Errata for “Mapping class group and a global Torelli theorem for hyperkähler manifolds”, Duke Math. J. 169 (2020), 1037–1038.Google Scholar
Vial, C., On the motive of some hyperkähler varieties, J. Reine Angew. Math. 2017 (2017), 235–247.CrossRefGoogle Scholar
Voisin, C., On the Chow ring of certain algebraic hyper-Kähler manifolds, Pure Appl. Math. Q. 4 (2008), 613–649.CrossRefGoogle Scholar
Voisin, C., Rational equivalence of 0-cycles on K3 surfaces and conjectures of Huybrechts and O'Grady, in Recent advances in algebraic geometry, London Mathematical Society Lecture Note Series, vol. 417 (Cambridge University Press, Cambridge, 2015), 422–436.Google Scholar
Voisin, C., Remarks and questions on coisotropic subvarieties and 0-cycles of hyper-Kähler varieties, in K3 surfaces and their moduli (Springer, 2016), 365–399.CrossRefGoogle Scholar
Voisin, C., Triangle varieties and surface decomposition of hyper-Kähler manifolds, in Recent developments in algebraic geometry: To Miles Reid for his 70th birthday, London Mathematical Society Lecture Note Series, vol. 478 (Cambridge University Press, 2022), 314–356.Google Scholar
Yau, S.-T. and Zaslow, E., BPS states, string duality, and nodal curves on $K3$, Nuclear Phys. B 471 (1996), 503–512.CrossRefGoogle Scholar
Yin, Q., Finite-dimensionality and cycles on powers of K3 surfaces, Comment. Math. Helv. 90 (2015), 503–511.CrossRefGoogle Scholar