Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-28T23:19:35.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Eisenstein cocycles in motivic cohomology

Part of: Discontinuous groups and automorphic forms $K$-theory in geometry

Published online by Cambridge University Press:  30 October 2024

Romyar Sharifi Open the ORCID record for Romyar Sharifi [Opens in a new window]  and
Akshay Venkatesh Open the ORCID record for Akshay Venkatesh [Opens in a new window]
Romyar Sharifi
Affiliation:
Department of Mathematics, University of California, 520 Portola Plaza, Los Angeles, CA 90095, USA [email protected]
Akshay Venkatesh
Affiliation:
School of Mathematics, Institute for Advanced Study, 1 Einstein Drive, Princeton, NJ 08540, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Several authors have studied homomorphisms from first homology groups of modular curves to 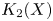$K_2(X)$, with 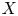$X$ either a cyclotomic ring or a modular curve. These maps send Manin symbols in the homology groups to Steinberg symbols of cyclotomic or Siegel units. We give a new construction of these maps and a direct proof of their Hecke equivariance, analogous to the construction of Siegel units using the universal elliptic curve. Our main tool is a 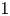$1$-cocycle from 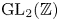$\mathrm {GL}_2(\mathbb {Z})$ to the second 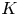$K$-group of the function field of a suitable group scheme over 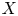$X$, from which the maps of interest arise by specialization.

Keywords

Eisenstein cocyclesManin symbolsSteinberg symbolsmotivic cohomology

MSC classification

Primary: 11F75: Cohomology of arithmetic groups 19E15: Algebraic cycles and motivic cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 10 , October 2024 , pp. 2407 - 2479
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bannai, K., Hagihara, K., Yamada, K. and Yamamoto, S., Canonical equivariant cohomology classes generating zeta values of totally real fields, Trans. Amer. Math. Soc. Ser. B 10 (2023), 613–635.CrossRefGoogle Scholar
Barvinok, A. and Pommersheim, J., An algorithmic theory of lattice points in polyhedra, in New perspectives in algebraic combinatorics, Mathematical Sciences Research Institute Publications, vol. 38 (Cambridge University Press, Cambridge, 1999), 91–147.Google Scholar
Beilinson, A., Higher regulators of modular curves, in Applications of algebraic K-theory to algebraic geometry and number theory, Part I (Boulder, Colo., 1983), Contemporary Mathematics, vol. 55 (American Mathematical Society, Providence, RI, 1986), 1–34.Google Scholar
Beilinson, A., Kings, G. and Levin, A., Topological polylogarithms and $p$-adic interpolation of $L$-values of totally real fields, Math. Ann. 371 (2018), 1449–1495.CrossRefGoogle Scholar
Beilinson, A. and Levin, A., The elliptic polylogarithm, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, vol. 55, Part 2 (American Mathematical Society, Providence, RI, 1994), 123–190.Google Scholar
Bergeron, N., Charollois, P. and Garcia, L., Transgressions of the Euler class and Eisenstein cohomology of $\mathrm {GL}_n(\mathbf {Z})$, Jpn. J. Math. 15 (2020), 371–379.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and higher $K$-theory, Adv. Math. 61 (1986), 267–304.CrossRefGoogle Scholar
Bloch, S., The moving lemma for higher Chow groups, J. Algebraic Geom. 3 (1994), 537–568.Google Scholar
Brion, M., Points entiers dans les polyédres convexes, Ann. Sci. Éc. Norm. Supér. 21 (1988), 653–663.CrossRefGoogle Scholar
Brunault, F., Beilinson-Kato elements in $K_2$ of modular curves, Acta Arith. 134 (2008), 283–298.CrossRefGoogle Scholar
Brunault, F., On the $K_4$ group of modular curves, Preprint (2022), arXiv:2009.07614v2.Google Scholar
Busuioc, C., The Steinberg symbols and special values of $L$-functions, Trans. Amer. Math. Soc. 360 (2008), 5999–6015.CrossRefGoogle Scholar
Déglise, F., Motifs génériques, Rend. Semin. Mat. Univ. Padova 119 (2008), 173–244.CrossRefGoogle Scholar
Denniger, C. and Murre, J., Motivic decomposition of abelian schemes and the Fourier transform, J. Reine Angew. Math. 422 (1991), 201–219.Google Scholar
Edixhoven, B., The weight in Serre's conjectures on modular forms, Invent. Math. 109 (1992), 563–594.CrossRefGoogle Scholar
Faltings, G., Arithmetic Eisenstein classes on the Siegel space: some computations, in Number fields and function fields—two parallel worlds, Progress in Mathematics, vol. 239 (Birkhäuser, Boston, 2005), 133–166.CrossRefGoogle Scholar
Fukaya, T. and Kato, K., On conjectures of Sharifi, Kyoto J. Math. 64 (2024), 277–420.CrossRefGoogle Scholar
Fukaya, T., Kato, K. and Sharifi, R., Modular symbols in Iwasawa theory, in Iwasawa theory 2012, Contributions in Mathematical and Computational Sciences, vol. 7 (Springer, Heidelberg, 2014), 177–219.CrossRefGoogle Scholar
Fukaya, T., Kato, K. and Sharifi, R., Modular symbols and the integrality of zeta elements, Ann. Math. Qué. 40 (2016), 377–395, Special Issue on the Occasion of the 60th Birthday of Glenn Stevens (Part II).CrossRefGoogle Scholar
Fulton, W., Intersection theory, second edition (Springer, New York, 1998).CrossRefGoogle Scholar
Garoufalidis, S. and Pommersheim, J., Values of zeta functions at negative integers, Dedekind sums and toric geometry, J. Amer. Math. Soc. 14 (2001), 1–23.CrossRefGoogle Scholar
Geisser, T., Motivic cohomology over Dedekind rings, Math. Z. 248 (2004), 773–794.CrossRefGoogle Scholar
Goncharov, A., Euler complexes and the geometry of modular varieties, Geom. Funct. Anal. 17 (2008), 1872–1914.CrossRefGoogle Scholar
Goncharov, A., Motivic fundamental group of $\mathbb {G}_m-\mu _N$ and modular manifolds, Preprint (2019), arXiv:1910.10321v1.Google Scholar
Hesselholt, L., Norm maps in Milnor $K$-theory, Unpublished note (2005).Google Scholar
Hida, H., Galois representations into $\mathrm {GL}_2(\mathbf {Z}_p{X})$ attached to ordinary cusp forms, Invent. Math. 85 (1986), 545–613.CrossRefGoogle Scholar
Huber, A. and Kings, G., Polylogarithm for families of commutative group schemes, J. Algebraic Geom. 27 (2018), 449–495.CrossRefGoogle Scholar
Kato, K., p-adic Hodge theory and values of zeta functions of modular forms, in Cohomologies p-adiques et applications arithmetiques III, Astérisque, vol. 295 (Société Mathématique de France, Paris, 2004), 117–290.Google Scholar
Kings, G. and Rössler, D., Higher analytic torsion, polylogarithms and norm-compatible elements of abelian schemes, in Geometry, analysis and probability, Progress in Mathematics, vol. 310 (Birkhäuser/Springer, Cham, 2017), 99–126.CrossRefGoogle Scholar
Kings, G. and Sprang, J., Eisenstein-Kronecker classes, integrality of critical values of Hecke $L$-functions and $p$-adic interpolation, Preprint (2024), arXiv:1912.03657v3.Google Scholar
Kirby, R. and Melvin, P., Dedekind sums, $\mu$-invariants and the signature cocycle, Math. Ann. 299 (1994), 231–267.CrossRefGoogle Scholar
Lecouturier, E., Higher Eisenstein elements, higher Eichler formulas and rank of Hecke algebras, Invent. Math. 223 (2021), 485–595.CrossRefGoogle Scholar
Lecouturier, E. and Wang, J., On a conjecture of Sharifi and Mazur's Eisenstein ideal, Int. Math. Res. Not. 2022 (2022), 391–421.CrossRefGoogle Scholar
Levine, M., Techniques of localization in the theory of algebraic cycles, J. Algebraic Geom. 10 (1999), 299–363.Google Scholar
Levine, M., $K$-theory and motivic cohomology of schemes, I, Preprint (2004).Google Scholar
Lim, S. and Park, J., Milnor $K$-theory and the Shintani cocycle, Preprint (2019), arXiv:1909.03450v1.Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture notes on motivic cohomology, Clay Mathematics Monographs, vol. 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Nekovář, J. and Scholl, A., Introduction to plectic cohomology, in Advances in the theory of automorphic forms and their L-functions, Contemporary Mathematics, vol. 664 (American Mathematical Society, Providence, RI, 2016), 321–337.CrossRefGoogle Scholar
Nori, M., Some Eisenstein cohomology classes for the integral unimodular group, in Proceedings of the International Congress of Mathematicians (Zürich, 1994) (Birkhäuser, Basel, 1995), 690–696.CrossRefGoogle Scholar
Ohta, M., Companion forms and the structure of $p$-adic Hecke algebras, J. Reine Angew. Math. 585 (2005), 141–172.CrossRefGoogle Scholar
Pappas, G., Integral Grothendieck-Riemann-Roch theorem, Invent. Math. 170 (2007), 455–481.CrossRefGoogle Scholar
Rademacher, H. and Grosswald, E., Dedekind sums, Carus Mathematical Monographs, vol. 16 (Mathematical Association of America, Washington, DC, 1972).CrossRefGoogle Scholar
Rosen, J. and Shnidman, A., Extensions of CM elliptic curves and orbit counting on the projective line, Res. Number Theory 3 (2017), Paper No. 9, 13 pp.CrossRefGoogle Scholar
Rost, M., Chow groups with coefficients, Doc. Math. 1 (1996), 319–393.CrossRefGoogle Scholar
Sczech, R., Eisenstein group cocycles for $\mathrm {GL}_n$ and values of $L$-functions, Invent. Math. 113 (1993), 581–616.CrossRefGoogle Scholar
Sharifi, R., A reciprocity map and the two-variable $p$-adic $L$-function, Ann. of Math. 173 (2011), 251–300.CrossRefGoogle Scholar
Sharifi, R., Modular curves and cyclotomic fields, Lecture notes for the 2018 Arizona Winter School, http://swc.math.arizona.edu/aws/2018/2018SharifiNotes.pdf.Google Scholar
Shimura, G., Introduction to the arithmetic theory of automorphic functions (Princeton University Press, Princeton, NJ, 1994).Google Scholar
Solomon, D., Algebraic properties of Shintani's generating functions: Dedekind sums and cocycles on $\mathrm {PGL}_2(\mathbf {Q})$, Compos. Math. 112 (1998), 333–362.CrossRefGoogle Scholar
Soulé, C., K-théorie des anneaux d'entiers de corps de nombres et cohomologie étale, Invent. Math. 55 (1979), 251–295.CrossRefGoogle Scholar
Spitzweck, M., A commutative $\mathbb {P}^1$-spectrum representing motivic cohomology over Dedekind domains, Mém. Soc. Math. Fr. 157 (2018).Google Scholar
The Stacks Project Authors, Stacks Project, https://stacks.math.columbia.edu.Google Scholar
Stevens, G., $K$-theory and Eisenstein series, Preprint (2007), https://math.bu.edu/people/ghs/preprints/Circular-KThry-11-07.pdf.Google Scholar
Venkatesh, A., Derived Hecke algebra and cohomology of arithmetic groups, Forum Math. Pi 7 (2019), e7.CrossRefGoogle Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 188–238.Google Scholar
Wang, J., Invariants of modular curves and Sharifi's conjectures, PhD thesis, University of Arizona (2018).Google Scholar