Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-29T19:14:37.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagrams in the mod p cohomology of Shimura curves

Part of: Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields Lie groups

Published online by Cambridge University Press:  07 July 2021

Andrea Dotto  and
Daniel Le
Andrea Dotto
Affiliation:
University of Chicago, 5734 South University Avenue, Chicago, IL60637, [email protected]
Daniel Le
Affiliation:
Purdue University, 150 North University Street, West Lafayette, IN47907, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a local–global compatibility result in the mod 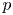$p$ Langlands program for 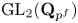$\mathrm {GL}_2(\mathbf {Q}_{p^f})$. Namely, given a global residual representation 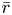$\bar {r}$ appearing in the mod 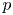$p$ cohomology of a Shimura curve that is sufficiently generic at 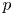$p$ and satisfies a Taylor–Wiles hypothesis, we prove that the diagram occurring in the corresponding Hecke eigenspace of mod 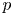$p$ completed cohomology is determined by the restrictions of 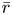$\bar {r}$ to decomposition groups at 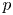$p$. If these restrictions are moreover semisimple, we show that the 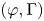$(\varphi ,\Gamma )$-modules attached to this diagram by Breuil give, under Fontaine's equivalence, the tensor inductions of the duals of the restrictions of 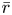$\bar {r}$ to decomposition groups at 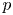$p$.

Keywords

Galois representationsmod p Langlands program

MSC classification

Primary: 11F80: Galois representations
Secondary: 11S37: Langlands-Weil conjectures, nonabelian class field theory 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 8 , August 2021 , pp. 1653 - 1723
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Breuil, C., Sur quelques représentations modulaires et $p$-adiques de ${\rm GL_2}({\boldsymbol Q}_p)$. I, Compos. Math. 138 (2003), 165–188; MR 2018825.10.1023/A:1026191928449CrossRefGoogle Scholar
Breuil, C., Diagrammes de Diamond et $(\phi , \Gamma )$-modules, Israel J. Math. 182 (2011), 349–382; MR 2783977.10.1007/s11856-011-0035-3CrossRefGoogle Scholar
Breuil, C., Sur un problème de compatibilité local–global modulo $p$ pour ${\rm GL_2}$, J. Reine Angew. Math. 692 (2014), 1–76; MR 3274546.10.1515/crelle-2012-0083CrossRefGoogle Scholar
Breuil, C. and Diamond, F., Formes modulaires de Hilbert modulo $p$ et valeurs d'extensions entre caractères galoisiens, Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 905–974; MR 3294620.10.24033/asens.2230CrossRefGoogle Scholar
Breuil, C. and Paškūnas, V., Towards a modulo $p$ Langlands correspondence for ${\rm GL_2}$, Mem. Amer. Math. Soc. 216 (2012); MR 2931521.Google Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre's conjecture for mod $\ell$ Galois representations over totally real fields, Duke Math. J. 155 (2010), 105–161; MR 2730374.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the $p$-adic local Langlands correspondence, Camb. J. Math. 4 (2016), 197–287; MR 3529394.10.4310/CJM.2016.v4.n2.a2CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the $p$-adic Langlands program for ${\rm GL_2}(\Bbb Q_p)$, Compos. Math. 154 (2018), 503–548; MR 3732208.10.1112/S0010437X17007606CrossRefGoogle Scholar
Caraiani, A. and Levin, B., Kisin modules with descent data and parahoric local models, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 181–213; MR 3764041.10.24033/asens.2354CrossRefGoogle Scholar
Caruso, X., David, A. and Mézard, A., Un calcul d'anneaux de déformations potentiellement Barsotti–Tate, Trans. Amer. Math. Soc. 370 (2018), 6041–6096; MR 3814324.10.1090/tran/6973CrossRefGoogle Scholar
Colmez, P., Représentations de ${\rm GL_2}({\boldsymbol Q}_p)$ et $(\phi , \Gamma )$-modules, Astérisque 330 (2010), 281–509; MR 2642409.Google Scholar
Colmez, P., Dospinescu, G., Paškūnas, V., The $p$-adic local Langlands correspondence for ${\rm GL_2}(\Bbb Q_p)$, Camb. J. Math. 2 (2014), 1–47; MR 3272011.10.4310/CJM.2014.v2.n1.a1CrossRefGoogle Scholar
Emerton, M., Local–global compatibility in the $p$-adic Langlands program for $\textrm {GL}_2/\mathbf {Q}$, Preprint (2011).Google Scholar
Emerton, M., Gee, T. and Herzig, F., Weight cycling and Serre-type conjectures for unitary groups, Duke Math. J. 162 (2013), 1649–1722; MR 3079258.10.1215/00127094-2266365CrossRefGoogle Scholar
Emerton, M., Gee, T. and Savitt, D., Lattices in the cohomology of Shimura curves, Invent. Math. 200 (2015), 1–96; MR 3323575.10.1007/s00222-014-0517-0CrossRefGoogle Scholar
Enns, J., On mod p local-global compatibility for unramified ${\rm GL}_3$, PhD thesis, University of Toronto (2018), https://tspace.library.utoronto.ca/bitstream/1807/91817/3/Enns_John_201811_PhD_thesis.pdf.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux. I, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 249–309; MR 1106901.Google Scholar
Gee, T., Herzig, F. and Savitt, D., General Serre weight conjectures, J. Eur. Math. Soc. (JEMS) 20 (2018), 2859–2949; MR 3871496.10.4171/JEMS/826CrossRefGoogle Scholar
Gee, T., Liu, T. and Savitt, D., The weight part of Serre's conjecture for $\mathrm {GL}(2)$, Forum Math. Pi 3 (2015), e2; MR 3324938.CrossRefGoogle Scholar
Gee, T. and Newton, J., Patching and the completed homology of locally symmetric spaces, J. Inst. Math. Jussieu (2020), doi:10.1017/S1474748020000158.CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 231; MR 0199181.Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001), with an appendix by Vladimir G. Berkovich; MR 1876802.Google Scholar
Herzig, F., The weight in a Serre-type conjecture for tame $n$-dimensional Galois representations, Duke Math. J. 149 (2009), 37–116; MR 2541127.10.1215/00127094-2009-036CrossRefGoogle Scholar
Herzig, F., Le, D. and Morra, S., On ${\rm mod}\, p$ local–global compatibility for ${\rm GL_3}$ in the ordinary case, Compos. Math. 153 (2017), 2215–2286; MR 3705291.CrossRefGoogle Scholar
Hu, Y., Sur quelques représentations supersingulières de ${\rm GL_2}(\Bbb Q_p^f)$, J. Algebra 324 (2010), 1577–1615; MR 2673752.CrossRefGoogle Scholar
Hu, Y., Valeurs spéciales de paramètres de diagrammes de Diamond, Bull. Soc. Math. France 144 (2016), 77–115; MR 3481262.10.24033/bsmf.2707CrossRefGoogle Scholar
Hu, Y. and Wang, H., Multiplicity one for the mod $p$ cohomology of Shimura curves: the tame case, Math. Res. Lett. 25 (2018), 843–873; MR 3847337.CrossRefGoogle Scholar
Ireland, K. and Rosen, M., A classical introduction to modern number theory, second edition, Graduate Texts in Mathematics, vol. 84 (Springer, New York, 1990); MR 1070716.10.1007/978-1-4757-2103-4CrossRefGoogle Scholar
Kisin, M., Crystalline representations and F-crystals, in Algebraic geometry and number theory, Progress in Mathematics, vol. 253 (Birkhäuser, Boston, MA, 2006), 459–496; MR 2263197 (2007j:11163).10.1007/978-0-8176-4532-8_7CrossRefGoogle Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21 (2008), 513–546; MR 2373358.CrossRefGoogle Scholar
Kisin, M., The Fontaine–Mazur conjecture for ${\rm GL_2}$, J. Amer. Math. Soc. 22 (2009), 641–690; MR 2505297.10.1090/S0894-0347-09-00628-6CrossRefGoogle Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. of Math. (2) 170 (2009), 1085–1180; MR 2600871.10.4007/annals.2009.170.1085CrossRefGoogle Scholar
Kisin, M., Deformations of $G_{\Bbb Q_p}\!$ and ${\rm GL_2}(\Bbb Q_p)$ representations, Astérisque 330 (2010), 511–528; MR 2642410.Google Scholar
Le, D., Multiplicity one for wildly ramified representations, Algebra Number Theory 13 (2019), 1807–1827; MR 4017535.10.2140/ant.2019.13.1807CrossRefGoogle Scholar
Le, D., Le Hung, B. V. and Levin, B., Weight elimination in Serre-type conjectures, Duke Math. J. 168 (2019), 2433–2506; MR 4007598.CrossRefGoogle Scholar
Le, D., Le Hung, B. V., Levin, B. and Morra, S., Potentially crystalline deformation rings and Serre weight conjectures: shapes and shadows, Invent. Math. 212 (2018), 1–107; MR 3773788.10.1007/s00222-017-0762-0CrossRefGoogle Scholar
Le, D., Le Hung, B. V., Levin, B. and Morra, S., Serre weights and Breuil's lattice conjecture in dimension three, Forum Math. Pi 8 (2020), e5; MR 4079756.CrossRefGoogle Scholar
Le, D., Morra, S. and Park, C., On ${\rm mod}\, p$ local–global compatibility for ${\rm GL_3}(\Bbb Q_p)$ in the non-ordinary case, Proc. Lond. Math. Soc. (3) 117 (2018), 790–848; MR 3873135.10.1112/plms.12148CrossRefGoogle Scholar
Le, D., Morra, S. and Schraen, B., Multiplicity one at full congruence level, J. Inst. Math. Jussieu (2020), doi:10.1017/S1474748020000225.CrossRefGoogle Scholar
Park, C. and Qian, Z., On mod p local–global compatibility for $\mathrm {GL}_n(\mathbf {Q}_p)$ in the ordinary case, Mém. Soc. Math. Fr., to appear. Preprint (2018), arXiv:1712.03799.Google Scholar
Paškūnas, V., The image of Colmez's Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191; MR 3150248.CrossRefGoogle Scholar
Scholze, P., On the $p$-adic cohomology of the Lubin-Tate tower, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 811–863, with an appendix by Michael Rapoport; MR 3861564.10.24033/asens.2367CrossRefGoogle Scholar