Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-30T08:52:03.182Z Has data issue: false hasContentIssue false
  • English
  • Français

Sheaf quantization of Legendrian isotopy

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  17 February 2023

Peng Zhou
Peng Zhou*
Affiliation:
University of California, Berkeley, 970 Evans Hall, Berkeley, CA 94720, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 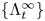$\{\Lambda ^\infty _t\}$ be an isotopy of Legendrians (possibly singular) in a unit cosphere bundle 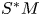$S^*M$ that arise as slices of a singular Legendrian 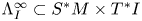$\Lambda _I^\infty \subset S^*M \times T^*I$. Let 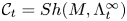$\mathcal {C}_t = Sh(M, \Lambda ^\infty _t)$ be the differential graded derived category of constructible sheaves on 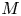$M$ with singular support at infinity contained in 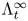$\Lambda ^\infty _t$. We prove that if the isotopy of Legendrians embeds into an isotopy of Liouville hypersurfaces, then the family of categories 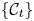$\{\mathcal {C}_t\}$ is constant in 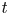$t$.

Keywords

nearby cyclesingular support estimate

MSC classification

Primary: 53D25: Geodesic flows
Secondary: 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 2 , February 2023 , pp. 419 - 435
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by an IHES Simons Postdoctoral Fellowship as part of the Simons Collaboration on HMS.

In memory of Steve

References

Geiges, H., An introduction to contact topology, Cambridge Studies in Advanced Mathematics, vol. 109 (Cambridge University Press, 2008).Google Scholar
Ganatra, S., Pardon, J. and Shende, V., Microlocal Morse theory of wrapped Fukaya categories, Preprint (2018), arXiv:1809.08807.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., Sectorial descent for wrapped Fukaya categories, Preprint (2018), arXiv:1809.03427.Google Scholar
Guillermou, S., Kashiwara, M. and Schapira, P., Sheaf quantization of Hamiltonian isotopies and applications to nondisplaceability problems, Duke Math. J. 161 (2012), 201–245.CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds, Grundlehren der mathematischen Wissenschaften, vol. 292 (Springer, 2013).Google Scholar
Nadler, D., Non-characteristic expansions of Legendrian singularities, Preprint (2015), arXiv:1507.01513.Google Scholar
Nadler, D., Wrapped microlocal sheaves on pairs of pants, Preprint (2016), arXiv:1604.00114.Google Scholar
Nadler, D. and Shende, V., Sheaf quantization in Weinstein symplectic manifolds, Preprint (2020), arXiv:2007.10154.Google Scholar
Nadler, D. and Zaslow, E., Constructible sheaves and the Fukaya category, J. Amer. Math. Soc. 22 (2009), 233–286.Google Scholar
Tamarkin, D., Microlocal condition for non-displaceablility, Preprint (2008), arXiv:0809.1584.Google Scholar
Treumann, D., Williams, H. and Zaslow, E., Kasteleyn operators from mirror symmetry, Selecta Math. (N.S.) 25 (2019), 60.Google Scholar