Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-29T00:10:26.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative hyperbolicity of free-by-cyclic extensions

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  30 January 2023

Pritam Ghosh
Pritam Ghosh*
Affiliation:
Department of Mathematics, Ashoka University, Haryana 131029, India [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finitely generated free group 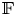$ {\mathbb {F} }$ of 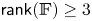$\mathsf {rank}( {\mathbb {F} } )\geq 3$, we show that the mapping torus of 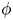$\phi$ is (strongly) relatively hyperbolic if 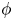$\phi$ is exponentially growing. As a corollary of our work, we give a new proof of Brinkmann's theorem which proves that the mapping torus of an atoroidal outer automorphism is hyperbolic. We also give a new proof of the Bridson–Groves theorem that the mapping torus of a free group automorphism satisfies the quadratic isoperimetric inequality. Our work also solves a problem posed by Minasyan and Osin: the mapping torus of an outer automorphism is not virtually acylindrically hyperbolic if and only if 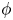$\phi$ has finite order.

Keywords

free groupsouter automorphismstrain-track mapsrelative hyperbolicitymapping torusfree-by-cyclic groups

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20E05: Free nonabelian groups 20F67: Hyperbolic groups and nonpositively curved groups 57M07: Topological methods in group theory
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 1 , January 2023 , pp. 153 - 183
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author was supported by a faculty research grant from Ashoka University during this project.

References

Behrstock, J., Drutu, C. and Mosher, L., Thick metric spaces, relative hyperbolicity and quasi-isometric rigidity, Math. Ann. 344 (2009), 543–595.CrossRefGoogle Scholar
Bestvina, M. and Feighn, M., A combination theorem for negetively curved groups, J. Differential Geom. 43 (1992), 85–101.Google Scholar
Bestvina, M., Feighn, M. and Handel, M., Tits alternative in Out$(F_n)$-I: Dynamics of exponentially-growing automorphisms, Ann. of Math. 151 (2000), 517–623.CrossRefGoogle Scholar
Bestvina, M., Feighn, M. and Handel, M., The Tits alternative for Out$(F_n)$ II: A Kolchin type theorem, Ann. of Math. 161 (2005), 1–59.CrossRefGoogle Scholar
Bestvina, M. and Handel, M., Train tracks and automorphisms of free groups, Ann. of Math. 135 (1992), 1–51.CrossRefGoogle Scholar
Bestvina, M., Handel, M. and Feighn, M., Laminations, trees, and irreducible automorphisms of free groups, Geom. Funct. Anal. 7 (1997), 215–244.CrossRefGoogle Scholar
Bowditch, B., The Cannon–Thurston map for punctured-surface groups, Math. Z. 255 (2007), 35–76.CrossRefGoogle Scholar
Bowditch, B., Relatively hyperolic groups, Internat. J. Algebra Comput. 22 (2012), 1250016.CrossRefGoogle Scholar
Bridson, M. and Groves, D., The quadratic isoperimetric inequality for mapping tori of free group automorphisms, Mem. Amer. Math. Soc. 203 (2010), 1–152.Google Scholar
Brinkmann, P., Hyperbolic automorphisms of free groups, Geom. Funct. Anal. 10 (2000), 1071–1089.CrossRefGoogle Scholar
Button, J. and Kropholler, R., Nonhyperbolic free-by-cyclic and one-relator groups, New York J. Math. 22 (2016), 755–774.Google Scholar
Dowdall, S. and Taylor, S., Hyperbolic extensions of free groups, Geom. Topol. 22 (2018), 517–570.CrossRefGoogle Scholar
Drutu, C., Relatively hyperbolic groups: geometry and quasi-isometric invariance, Comment. Math. Helv. 84 (2009), 503–546.CrossRefGoogle Scholar
Farb, B., Relatively hyperolic groups, Geom. Funct. Anal. 8 (1998), 810–840.CrossRefGoogle Scholar
Feighn, M. and Handel, M., The recognition theorem for Out$(F_n)$, Groups Geom. Dyn. 5 (2011), 39–106.CrossRefGoogle Scholar
Gautero, F., Geodesics in trees of hyperbolic and relatively hyperbolic spaces, Proc. Edinb. Math. Soc. 59 (2016), 701–740.CrossRefGoogle Scholar
Gautero, F. and Lustig, M., The mapping torus group of a free group automorphism is hyperbolic relative to the canonical subgroups of polynomial growth, Preprint (2007), arXiv:0707.0822.Google Scholar
Genevois, A. and Horbez, C., Acylindrical hyperbolicity of automorphism groups of infinitely-ended groups, J. Topol. 14 (2021), 963–991.CrossRefGoogle Scholar
Ghosh, P., Relatively irreducible free subgroups of Out $(\mathbb {F})$, Preprint (2018), arXiv:1210.8081.Google Scholar
Ghosh, P., Limits of conjugacy classes under iterates of hyperbolic elements of Out$(\mathbb {F})$, Groups Geom. Dyn. 4 (2021), 177–211.Google Scholar
Hagen, M., A remark on thickness of free-by-cyclic groups, Illinois J. Math. 63 (2019), 633–643.CrossRefGoogle Scholar
Hagen, M. and Wise, D., Cubulating mapping tori of polynomial growth free group automorphisms, Preprint (2016), arXiv:1605.07879.Google Scholar
Handel, M. and Mosher, L., Subgroup classification in Out $(F_n)$, Preprint (2009), arXiv:0908.1255.Google Scholar
Handel, M. and Mosher, L., Subgroup decomposition in Out$(F_n)$, Mem. Amer. Math. Soc. 264 (2020).Google Scholar
Macura, N., Quadratic isoperimetric inequality for mapping tori of polynomially growing outer automorphisms of free groups, Geom. Funct. Anal. 10 (2000), 874–901.CrossRefGoogle Scholar
Macura, N., Detour functions and quasi-isometries, Q. J. Math. 53 (2002), 207–239.CrossRefGoogle Scholar
Minasyan, A. and Osin, D., Acylindrical hyperbolicity of groups acting on trees, Math. Ann. 362 (2015), 1055–1105.CrossRefGoogle Scholar
Mj, M. and Reeves, L., A combination theorem for strong relative hyperolicity, Geom. Topol. 12 (2008), 1777–1798.CrossRefGoogle Scholar
Mosher, L., A hyperbolic-by-hyperbolic hyperbolic group, Proc. Amer. Math. Soc. 125 (1997), 3447–3455.CrossRefGoogle Scholar
Sisto, A., On metric relative hyperbolicity, Preprint (2012), arXiv:1210.8081.Google Scholar
Uyanik, C., Hyperbolic extensions of free groups using atoroidal ping-pong, Algebr. Geom. Topol. 19 (2019), 1385–1411.CrossRefGoogle Scholar