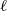Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-28T16:08:24.766Z Has data issue: false hasContentIssue false
  • English
  • Français

Independence of $\ell $-adic Galois representations over function fields

Part of: Arithmetic algebraic geometry (Co)homology theory

Published online by Cambridge University Press:  25 April 2013

Wojciech Gajda  and
Sebastian Petersen
Wojciech Gajda
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Umultowska 87, 61614 Poznań, Poland (email: [email protected])
Sebastian Petersen
Affiliation:
FB 10 - Mathematik und Naturwissenschaften, Universität Kassel, Heinrich-Plett-Str. 40, 34132 Kassel, Germany (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 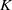$K$ be a finitely generated extension of 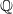$\mathbb {Q}$. We consider the family of 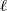$\ell $-adic representations (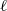$\ell $ varies through the set of all prime numbers) of the absolute Galois group of 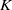$K$, attached to 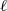$\ell $-adic cohomology of a separated scheme of finite type over 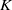$K$. We prove that the fields cut out from the algebraic closure of 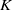$K$by the kernels of the representations of the family are linearly disjoint over a finite extension of K. This gives a positive answer to a question of Serre.

Keywords

Galois representationétale cohomologyabelian varietyfinitely generated field

MSC classification

Secondary: 11G10: Abelian varieties of dimension $> 1$ 14F20: Étale and other Grothendieck topologies and (co)homologies
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 7 , July 2013 , pp. 1091 - 1107
Copyright
Copyright © 2013 The Author(s) 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[Art55]Artin, E., The orders of the classical simple groups, Comm. Pure Appl. Math. 8 (1955), 455–472.Google Scholar
[EGAII]Grothendieck, A., Éléments de géométrie algébrique (rédigé avec la cooperation de Jean Dieudonné): II. Étude globale élémentaire de quelques classes de morphismes, Publ. Math. Inst. Hautes Études Sci. 8 (1961), 5–222.Google Scholar
[EGAIV3]Grothendieck, A., Éléments de géométrie algébrique (rédigé avec la cooperation de Jean Dieudonné): IV. Étude locale des schémas et des morphismes des schémas, Troisième partie, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.Google Scholar
[FJ05]Fried, M. D. and Jarden, M., Field arithmetic, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11, 2nd revised and enlarged ed (Springer, Berlin, 2005).Google Scholar
[Ill]Illusie, L., Constructibilité générique et uniformité en $\ell $, Preprint.Google Scholar
[KL81]Katz, N. and Lang, S., Finiteness theorems in geometric class field theory, Enseign. Math. 27 (1981), 285–319.Google Scholar
[KL86]Katz, N. and Laumon, G., Transformation de Fourier et majoration de sommes exponentielles, Publ. Math. Inst. Hautes Études Sci. 62 (1986), 361–418. Erratum: Publ. Math. Inst. Hautes Études Sci. 69 (1989), 244.Google Scholar
[KLST90]Kimmerle, W., Lyons, R., Sandling, R. and Teague, D., Composition factors from the group ring and Artin’s theorem on orders of simple groups, Proc. Lond. Math. Soc. 60 (1990), 89–122.Google Scholar
[Mil80]Milne, J., Étale cohomology (Princeton University Press, New Jersey, 1980).Google Scholar
[Nor87]Nori, M., On subgroups of $GL_n(\mathbb {F}_p)$, Invent. Math. (1987), 257–275.Google Scholar
[Ser94]Serre, J.-P., Propriétés conjecturales des groupes de Galois motiviques et des représentations $\ell $-adiques, Proc. Sympos. Pure Math. (1994), 377–400.Google Scholar
[Ser00]Serre, J.-P., Lettre à Ken Ribet du 7/3/1986, in Œuvres. Collected papers, IV, 1985–1998 (Springer, Berlin, 2000).Google Scholar
[Ser10]Serre, J.-P., Une critère d’indépendance pour une famille de représentations $\ell $-adiques, Preprint (2010), available at arXiv:1006.2442.Google Scholar
[SGA4]Artin, M., Grothendieck, A. and Verdier, J.-L., Séminaire de Géomt́rie Algébrique du Bois Marie 1963–64 - Théorie des topos et cohomologie étale des schémas (SGA 4), Lecture Notes in Mathematics, vol. 269, 270, 305 (Springer, 1972).Google Scholar
[SGA7]Grothendieck, A., Séminaire de Géométrie Algébrique du Bois Marie 1967–69 - Groupes de monodromy en géométrie algébrique (SGA 7), vol. 1, Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, 1972).Google Scholar