Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-28T13:17:24.588Z Has data issue: false hasContentIssue false
  • English
  • Français

BPS invariants from p-adic integrals

Part of: Projective and enumerative geometry Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  30 May 2024

Francesca Carocci Open the ORCID record for Francesca Carocci [Opens in a new window] ,
Giulio Orecchia  and
Dimitri Wyss
Francesca Carocci
Affiliation:
Mathematics Department, University of Geneva, Office 6.05, Rue du Conseil-Général 7-9, CH-1204 Geneva, Switzerland [email protected]
Giulio Orecchia
Affiliation:
White Oak Asset Management, Rue du Rhône 17, CH-1204 Geneva, Switzerland [email protected]
Dimitri Wyss
Affiliation:
Ecole Polytechnique Fédérale de Lausanne (EPFL), Chair of Arithmetic Geometry, CH-1015 Lausanne, Switzerland [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define 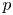$p$-adic 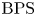$\mathrm {BPS}$ or 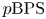$p\mathrm {BPS}$ invariants for moduli spaces 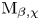$\operatorname {M}_{\beta,\chi }$ of one-dimensional sheaves on del Pezzo and K3 surfaces by means of integration over a non-archimedean local field 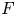$F$. Our definition relies on a canonical measure 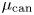$\mu _{\rm can}$ on the 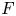$F$-analytic manifold associated to 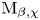$\operatorname {M}_{\beta,\chi }$ and the 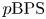$p\mathrm {BPS}$ invariants are integrals of natural 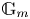${\mathbb {G}}_m$ gerbes with respect to 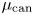$\mu _{\rm can}$. A similar construction can be done for meromorphic and usual Higgs bundles on a curve. Our main theorem is a 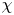$\chi$-independence result for these 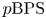$p\mathrm {BPS}$ invariants. For one-dimensional sheaves on del Pezzo surfaces and meromorphic Higgs bundles, we obtain as a corollary the agreement of 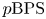$p\mathrm {BPS}$ with usual 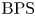$\mathrm {BPS}$ invariants through a result of Maulik and Shen [Cohomological 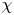$\chi$-independence for moduli of one-dimensional sheaves and moduli of Higgs bundles, Geom. Topol. 27 (2023), 1539–1586].

Keywords

moduli of sheavesDonaldson–Thomas invariantsp-adic integration

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 11S80: Other analytic theory (analogues of beta and gamma functions, $p$-adic integration, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 7 , July 2024 , pp. 1525 - 1550
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alper, J., Halpern-Leistner, D. and Heinloth, J., Existence of moduli spaces for algebraic stacks, Invent. Math. 234 (2023), 949–1038.10.1007/s00222-023-01214-4CrossRefGoogle Scholar
Altman, A. B. and Kleiman, S. L., Compactifying the Picard scheme, Adv. Math. 35 (1980), 50–112.10.1016/0001-8708(80)90043-2CrossRefGoogle Scholar
Arbarello, E. and Saccà, G., Singularities of moduli spaces of sheaves on K3 surfaces and Nakajima quiver varieties, Adv. Math. 329 (2018), 649–703.10.1016/j.aim.2018.02.003CrossRefGoogle Scholar
Bayer, A., Lahoz, M., Macrì, E., Nuer, H., Perry, A. and Stellari, P., Stability conditions in families, Publ. Math. Inst. Hautes Études Sci. 133 (2021), 157–325.10.1007/s10240-021-00124-6CrossRefGoogle Scholar
Beilinson, A., Bernstein, J., Deligne, P. and Gabber, O., Faisceaux pervers (Société Mathématique de France, Paris, 2018).10.24033/ast.1042CrossRefGoogle Scholar
Ben-Bassat, O., Brav, C., Bussi, V. and Joyce, D., A ‘Darboux theorem’ for shifted symplectic structures on derived Artin stacks, with applications, Geom. Topol. 19 (2015), 1287–1359.10.2140/gt.2015.19.1287CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge/A Series of Modern Surveys in Mathematics, vol. 21 (Springer, 2012).Google Scholar
Bousseau, P., A proof of N. Takahashi's conjecture for $(\mathbb {P}^2,E)$ and a refined sheaves/Gromov–Witten correspondence, Duke Math. J. 172 (2023), 2895–2955.10.1215/00127094-2022-0095CrossRefGoogle Scholar
Brav, C., Bussi, V., Dupont, D., Joyce, D. and Szendroi, B., Symmetries and stabilization for sheaves of vanishing cycles, J. Singul. 11 (2015), 85–151.Google Scholar
Brochard, S., Duality for commutative group stacks, Int. Math. Res. Not. IMRN 2021 (2021), 2321–2388.10.1093/imrn/rnz161CrossRefGoogle Scholar
Budur, N. and Zhang, Z., Formality conjecture for K3 surfaces, Compos. Math. 155 (2019), 902–911.10.1112/S0010437X19007206CrossRefGoogle Scholar
Chambert-Loir, A., Nicaise, J. and Sebag, J., Motivic integration (Springer, 2018), 305–361.10.1007/978-1-4939-7887-8_6CrossRefGoogle Scholar
Chaudouard, P.-H. and Laumon, G., Un théorème du support pour la fibration de Hitchin, Ann. Inst. Fourier (Grenoble) 66 (2016), 711–727.10.5802/aif.3023CrossRefGoogle Scholar
Crawley-Boevey, W., Geometry of the moment map for representations of quivers, Compos. Math. 126 (2001), 257–293.10.1023/A:1017558904030CrossRefGoogle Scholar
Davison, B., Purity and 2-Calabi-Yau categories, Preprint (2023), arXiv:2106.07692v4.10.1007/s00222-024-01279-9CrossRefGoogle Scholar
Davison, B., Hennecart, L. and Mejia, S. S., BPS Lie algebras for totally negative 2-Calabi-Yau categories and nonabelian Hodge theory for stacks, Preprint (2022), arXiv:2212.07668v2.Google Scholar
Davison, B., Hennecart, L. and Mejia, S. S., BPS algebras and generalised Kac-Moody algebras from 2-Calabi-Yau categories, Preprint (2023), arXiv:2303.12592v3.Google Scholar
Davison, B. and Meinhardt, S., Donaldson-Thomas theory for categories of homological dimension one with potential, Preprint (2015), arXiv:1512.08898.Google Scholar
Davison, B. and Meinhardt, S., Cohomological Donaldson–Thomas theory of a quiver with potential and quantum enveloping algebras, Invent. Math. 221 (2020), 777–871.10.1007/s00222-020-00961-yCrossRefGoogle Scholar
Deligne, P. and Mumford, D., The irreducibility of the space of curves of given genus, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 75–109.10.1007/BF02684599CrossRefGoogle Scholar
Fantechi, B., Goettsche, L. and Van Sraten, D., Euler number of the compactified Jacobian and multiplicity of rational curves, J. Algebraic Geom. 8 (1999), 115–133.Google Scholar
Fulton, W., Intersection theory (Princeton University Press, 2016).Google Scholar
Giraud, J., Cohomologie non abélienne, vol. 179 (Springer Nature, 2020).Google Scholar
Groechenig, M., Wyss, D. and Ziegler, P., Geometric stabilisation via p-adic integration, J. Amer. Math. Soc. 33 (2020), 807–873.10.1090/jams/948CrossRefGoogle Scholar
Groechenig, M., Wyss, D. and Ziegler, P., Mirror symmetry for moduli spaces of Higgs bundles via $p$-adic integration, Invent. Math. 221 (2020), 505–596.10.1007/s00222-020-00957-8CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique: IV. Etude locale des schémas et des morphismes de schémas, Seconde partie, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 5–231.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique: IV. Etude locale des schémas et des morphismes de schémas, Troisième partie, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.10.1007/BF02684343CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977); MR 0463157 (57 #3116).10.1007/978-1-4757-3849-0CrossRefGoogle Scholar
Hitchin, N., Stable bundles and integrable systems, Duke Math. J. 54 (1987), 91–114.10.1215/S0012-7094-87-05408-1CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, Aspects of Mathematics, vol. E31 (Friedr. Vieweg & Sohn, Braunschweig, 1997); MR 1450870 (98g:14012).10.1007/978-3-663-11624-0CrossRefGoogle Scholar
Huybrechts, D. and Thomas, R. P., Deformation-obstruction theory for complexes via Atiyah and Kodaira–Spencer classes, Math. Ann. 346 (2010), 545–569.10.1007/s00208-009-0397-6CrossRefGoogle Scholar
Igusa, J., An introduction to the theory of local zeta functions, AMS/IP Studies in Advanced Mathematics, vol. 14 (American Mathematical Society, Providence, RI, Cambridge, MA, 2000); MR 1743467.Google Scholar
Inaba, M.-A., Smoothness of the moduli space of complexes of coherent sheaves on an abelian or a projective K3 surface, Adv. Math. 227 (2011), 1399–1412.10.1016/j.aim.2011.03.001CrossRefGoogle Scholar
Joyce, D. D. and Song, Y., A theory of generalized Donaldson-Thomas invariants (American Mathematical Society, 2012).10.1090/S0065-9266-2011-00630-1CrossRefGoogle Scholar
Katz, S., Genus zero Gopakumar-Vafa invariants of contractible curves, J. Differential Geom. 79 (2008), 185–195.10.4310/jdg/1211512639CrossRefGoogle Scholar
Keel, S. and Mori, S., Quotients by groupoids, Ann. of Math. (2) 145 (1997), 193–213; MR 1432041 (97m:14014).10.2307/2951828CrossRefGoogle Scholar
Kinjo, T. and Koseki, N., Cohomological $\chi$-independence for Higgs bundles and Gopakumar-Vafa invariants, J. Eur. Math. Soc., to appear. Preprint (2021), arXiv:2112.10053.Google Scholar
Kontsevich, M. and Soibelman, Y., Stability structures, motivic Donaldson-Thomas invariants and cluster transformations, Preprint (2008), arXiv:0811.2435.Google Scholar
Langer, A., Moduli spaces of sheaves in mixed characteristic, Duke Math. J. 124 (2004), 571–586.10.1215/S0012-7094-04-12434-0CrossRefGoogle Scholar
Langer, A., Semistable sheaves in positive characteristic, Ann. of Math. (2) 159 (2004), 251–276.10.4007/annals.2004.159.251CrossRefGoogle Scholar
Langton, S. G., Valuative criteria for families of vector bundles on algebraic varieties, Ann. of Math. (2) 101 (1975), 88–110; MR 0364255 (51 #510).10.2307/1970987CrossRefGoogle Scholar
Lichtenbaum, S., Duality theorems for curves over p-adic fields, Invent. Math. 7 (1969), 120–136.10.1007/BF01389795CrossRefGoogle Scholar
Lieblich, M., Moduli of complexes on a proper morphism, J. Algebraic Geom. 15 (2006), 175–206.10.1090/S1056-3911-05-00418-2CrossRefGoogle Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, vol. 6 (Oxford University Press, Oxford, 2006).Google Scholar
López-Martín, A.C., Simpson Jacobians of reducible curves, J. Reine Angew. Math. 582 (2005), 1–39.10.1515/crll.2005.2005.582.1CrossRefGoogle Scholar
Maulik, D. and Shen, J., Cohomological $\chi$-independence for moduli of one-dimensional sheaves and moduli of Higgs bundles, Geom. Topol. 27 (2023), 1539–1586.10.2140/gt.2023.27.1539CrossRefGoogle Scholar
Maulik, D. and Thomas, R. P., Sheaf counting on local K3 surfaces, Pure Appl. Math. Q. 14 (2019), 419–441.10.4310/PAMQ.2018.v14.n3.a1CrossRefGoogle Scholar
Maulik, D. and Toda, Y., Gopakumar–Vafa invariants via vanishing cycles, Invent. Math. 213 (2018), 1017–1097.10.1007/s00222-018-0800-6CrossRefGoogle Scholar
Meinhardt, S., Donaldson–Thomas invariants vs. intersection cohomology for categories of homological dimension one, Preprint (2015), arXiv:1512.03343.Google Scholar
Mellit, A., Poincaré polynomials of moduli spaces of Higgs bundles and character varieties (no punctures), Invent. Math. 221 (2020), 301–327.10.1007/s00222-020-00950-1CrossRefGoogle Scholar
Melo, M., Rapagnetta, A. and Viviani, F., Fine compactified Jacobians of reduced curves, Trans. Amer. Math. Soc. 369 (2017), 5341–5402.10.1090/tran/6823CrossRefGoogle Scholar
Milne, J. S., Arithmetic duality theorems, Perspectives in Mathematics, vol. 1 (Academic Press, Boston, MA, 1986); MR 881804.Google Scholar
Mozgovoy, S. and O'Gorman, R., Counting twisted Higgs bundles, Preprint (2019), arXiv:1901.02439Google Scholar
Mozgovoy, S. and Schiffmann, O., Counting Higgs bundles, Preprint (2014), arXiv:1411.2101.Google Scholar
Mukai, S., Symplectic structure of the moduli space of sheaves on an abelian or K3 surface, Invent. Math. 77 (1984), 101–116.10.1007/BF01389137CrossRefGoogle Scholar
Ngô, B. C., Fibration de Hitchin et endoscopie, Invent. Math. 164 (2006), 399–453; MR 2218781 (2007k:14018).10.1007/s00222-005-0483-7CrossRefGoogle Scholar
Nitsure, N., Moduli space of semistable pairs on a curve, Proc. Lond. Math. Soc. (3) 62 (1991), 275–300; MR 1085642 (92a:14010).10.1112/plms/s3-62.2.275CrossRefGoogle Scholar
Pandharipande, R. and Thomas, R., Stable pairs and BPS invariants, J. Amer. Math. Soc. 23 (2010), 267–297.10.1090/S0894-0347-09-00646-8CrossRefGoogle Scholar
Poonen, B. and Stoll, M., The Cassels–Tate pairing on polarized abelian varieties, Ann. of Math. 150 (1999), 1109–1149.10.2307/121064CrossRefGoogle Scholar
Rego, C. J., The compactified Jacobian, Ann. Sci. Éc. Norm. Supér. (4) 13 (1980), 211–223; MR 584085 (81k:14006).10.24033/asens.1380CrossRefGoogle Scholar
Schoutens, H., The use of ultraproducts in commutative algebra (Springer, 2010).10.1007/978-3-642-13368-8CrossRefGoogle Scholar
Schiffmann, O., Indecomposable vector bundles and stable Higgs bundles over smooth projective curves, Ann. of Math. 183 (2016), 297–362.10.4007/annals.2016.183.1.6CrossRefGoogle Scholar
Serre, J.-P., Corps locaux, Deuxième édition, Publications de l'Université de Nancago, vol. VIII (Hermann, Paris, 1968); MR 0354618 (50 #7096).Google Scholar
Seshadri, C. S., Geometric reductivity over arbitrary base, Adv. Math. 26 (1977), 225–274.10.1016/0001-8708(77)90041-XCrossRefGoogle Scholar
Stacks Project Authors, Stacks project, http://math.columbia.edu/algebraic_geometry/stacks-git.Google Scholar
Thomas, R. P., A holomorphic Casson invariant for Calabi-Yau 3-folds, and bundles on K3 fibrations, J. Differential Geom. 54 (2000), 367–438.10.4310/jdg/1214341649CrossRefGoogle Scholar
Toda, Y., Multiple cover formula of generalized DT invariants I: parabolic stable pairs, Adv. Math. 257 (2014), 476–526.10.1016/j.aim.2014.02.031CrossRefGoogle Scholar
Toda, Y., Gopakumar–Vafa invariants and wall-crossing, J. Differential Geom. 123 (2023), 141–193.10.4310/jdg/1679503806CrossRefGoogle Scholar
Travkin, R., Quantum geometric Langlands correspondence in positive characteristic: The $\mathrm {GL}_{N}$ case, Duke Math. J. 165 (2016), 1283–1361.10.1215/00127094-3449780CrossRefGoogle Scholar
Vernet, T., Rational singularities for moment maps of totally negative quivers, Preprint (2022), arXiv:2209.14791.Google Scholar
Weil, A., Adeles and algebraic groups, vol. 23 (Springer, 2012).Google Scholar
Yasuda, T., The wild McKay correspondence and $p$-adic measures, J. Eur. Math. Soc. (JEMS) 19 (2017), 3709–3743.10.4171/jems/751CrossRefGoogle Scholar
Yu, H., Comptage des systémes locaux $\ell$-adiques sur une courbe, Ann. Math. 197 (2023), 423–531.10.4007/annals.2023.197.2.1CrossRefGoogle Scholar
Yuan, Y., Sheaves on non-reduced curves in a projective surface, Sci. China Math. 66 (2023), 237–250.10.1007/s11425-021-1964-4CrossRefGoogle Scholar