Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-30T01:16:21.164Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalisation of Varnavides’s theorem

Part of: Sequences and sets Extremal combinatorics

Published online by Cambridge University Press:  29 May 2024

Asaf Shapira
Asaf Shapira*
Affiliation:
School of Mathematics, Tel Aviv University, Tel Aviv, Israel
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A linear equation 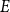$E$ is said to be sparse if there is 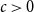$c\gt 0$ so that every subset of 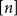$[n]$ of size 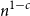$n^{1-c}$ contains a solution of 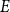$E$ in distinct integers. The problem of characterising the sparse equations, first raised by Ruzsa in the 90s, is one of the most important open problems in additive combinatorics. We say that 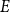$E$ in 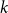$k$ variables is abundant if every subset of 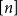$[n]$ of size 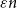$\varepsilon n$ contains at least 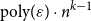$\text{poly}(\varepsilon )\cdot n^{k-1}$ solutions of 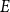$E$. It is clear that every abundant 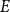$E$ is sparse, and Girão, Hurley, Illingworth, and Michel asked if the converse implication also holds. In this note, we show that this is the case for every 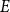$E$ in four variables. We further discuss a generalisation of this problem which applies to all linear equations.

Keywords

VarnavidesRuzsaRothsupersaturation

MSC classification

Primary: 05D99: None of the above, but in this section
Secondary: 11B75: Other combinatorial number theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 6 , November 2024 , pp. 724 - 728
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Supported in part by ERC Consolidator Grant 863438 and NSF-BSF Grant 20196.

References

Behrend, F. A. (1946) On sets of integers which contain no three terms in arithmetical progression. Proc Nat. Acad. Sci. USA 32(12) 331–332.CrossRefGoogle ScholarPubMed
Bloom, T. F. (2012) Translation invariant equations and the method of Sanders. Bull. Lond. Math. Soc. 44(5) 1050–1067.CrossRefGoogle Scholar
Bukh, B. (to appear) Extremal graphs without exponentially-small bicliques. Duke Math. J.Google Scholar
Conlon, D., Kim, J. H., Lee, C. and Lee, J. (2018) Some advances on Sidorenko’s conjecture. J. London Math. Soc. 98(3) 593–608.CrossRefGoogle Scholar
Erdős, P. and Simonovits, M. (1983) Supersaturated graphs and hypergraphs. Combinatorica 3(2) 181–192.CrossRefGoogle Scholar
Girão, A., Hurley, E., Illingworth, F. and Michel, L. Abundance: asymmetric graph removal lemmas and integer solutions to linear equations. arXiv: 2310.18202.Google Scholar
Kelley, Z. and Meka, R. (2023) Strong bounds for 3-progressions. arXiv: 2302.05537.CrossRefGoogle Scholar
Kosciuszko, T. Counting solutions to invariant equations in dense sets. arXiv: 2306.08567.Google Scholar
Ruzsa, I. Z. (1993) Solving a linear equation in a set of integers I. Acta Arith. 65(3) 259–282.CrossRefGoogle Scholar
Schoen, T. and Sisask, O. (2016) Roth’s theorem for four variables and additive structures in sums of sparse sets. Forum Math. Sigma 4 e5,28.CrossRefGoogle Scholar
Varnavides, P. (1959) On certain sets of positive density. J. London Math. Soc 34(3) 358–360.CrossRefGoogle Scholar