Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-29T23:25:08.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Tree structure of spectra of spectral Moran measures with consecutive digits

Part of: Harmonic analysis in one variable Classical measure theory Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  22 December 2023

Cong Wang  and
Feng-Li Yin
Cong Wang
Affiliation:
School of Mathematical Sciences, Henan Institute of Science and Technology, Xinxiang 453003, P. R. China e-mail: [email protected]
Feng-Li Yin*
Affiliation:
School of Mathematics and Statistics, Zhoukou Normal University, Zhoukou 466001, P. R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 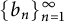$\{b_n\}_{n=1}^{\infty }$ be a sequence of integers larger than 1. We will study the harmonic analysis of the equal-weighted Moran measures 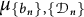$\mu _{\{b_n\},\{{\mathcal D}_n\}}$ with 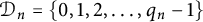${\mathcal D}_n=\{0,1,2,\ldots ,q_n-1\}$, where 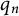$q_n$ divides 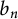$b_n$ for all 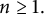$n\geq 1.$ In this paper, we first characterize all the maximal orthogonal sets of 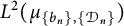$L^2(\mu _{\{b_n\},\{{\mathcal D}_n\}})$ via a tree mapping. By this characterization, we give some sufficient conditions for the maximal orthogonal set to be an orthonormal basis.

Keywords

Spectral measuresspectraMoran measuresorthonormal basis

MSC classification

Primary: 28A80: Fractals 42C05: Orthogonal functions and polynomials, general theory 42A65: Completeness of sets of functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 3 , September 2024 , pp. 593 - 610
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the National Natural Science Foundation of China (Grant No. 12101196) and the Natural Science Foundation of Henan Province (Grant No. 212300410323).

References

An, L. X., Fu, X. Y., and Lai, C. K., On spectral Cantor–Moran measures and a variant of Bourgain’s sum of sine problem . Adv. Math. 349(2019), 84–124.CrossRefGoogle Scholar
An, L. X. and He, X. G., A class of spectral Moran measures . J. Funct. Anal. 266(2014), 343–354.CrossRefGoogle Scholar
An, L. X. and Wang, C., On self-similar spectral measures . J. Funct. Anal. 280(2021), 108821.CrossRefGoogle Scholar
Chen, M. L., Liu, J. C., and Wang, X. Y., Spectrality of a class of self-affine measures on ${\mathbb{R}}^2$ . Nonlinearity 34(2021), 7446–7469.CrossRefGoogle Scholar
Dai, X. R., Spectra of Cantor measures . Math. Ann. 366(2016), 1621–1647.CrossRefGoogle Scholar
Dai, X. R., Fu, X. Y., and Yan, Z. H., Spectrality of self-affine Sierpinski-type measures on ${\mathbb{R}}^2$ . Appl. Comput. Harmon. Anal. 52(2021), 63–81.CrossRefGoogle Scholar
Dai, X. R., He, X. G., and Lai, C. K., Spectral property of Cantor measures with consecutive digits . Adv. Math. 242(2013), 187–208.CrossRefGoogle Scholar
Dai, X. R. and Sun, Q. Y., Spectral measures with arbitrary Hausdorff dimensions . J. Funct. Anal. 268(2015), 2464–2477.CrossRefGoogle Scholar
Deng, Q. R., Dong, X. H., and Li, M. T., Tree structure of spectra of spectral self-affine measures . J. Funct. Anal. 277(2019), 937–957.CrossRefGoogle Scholar
Dutkay, D., Han, D. G., and Sun, Q. Y., On spectra of a Cantor measure . Adv. Math. 221(2009), 251–276.CrossRefGoogle Scholar
Dutkay, D., Han, D. G., and Sun, Q. Y., Divergence of the mock and scrambled Fourier series on fractal measures . Trans. Amer. Math. Soc. 366(2014), 2191–2208.CrossRefGoogle Scholar
Dutkay, D. and Haussermann, J., Number theory problem from the harmonic analysis of a fractal . J. Number Theory 159(2016), 7–26.CrossRefGoogle Scholar
Falconer, K. J., Fractal geometry, mathematical foundations and applications, Wiley, New York, 1990.Google Scholar
Fu, Y. S., He, X. G., and Wen, Z. X., Spectra of Bernoulli convolutions and random convolutions . J. Math. Pures Appl. 116(2018), 105–131.CrossRefGoogle Scholar
Fu, Y. S. and Wang, C., Spectra of a class of Cantor–Moran measures with three-element digit sets . J. Approx. Theory 261(2021), 105494.CrossRefGoogle Scholar
Fuglede, B., Commuting self-adjoint partial differential operators and a group theoretic problem . J. Funct. Anal. 16(1974), 101–121.CrossRefGoogle Scholar
Hu, T. Y. and Lau, K. S., Spectral property of the Bernoulli convolution . Adv. Math. 219(2008), 554–567.CrossRefGoogle Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal ${L}^2$ spaces. J. Anal. Math. 75(1998), 185–228.Google Scholar
Łaba, I. and Wang, Y., On spectral Cantor measures . J. Funct. Anal. 193(2002), 409–420.CrossRefGoogle Scholar
Li, J. L., Spectra of a class of self-affine measures . J. Funct. Anal. 260(2011), 1086–1095.CrossRefGoogle Scholar
Lu, Z. Y., Dong, X. H., and Liu, Z. S., Spectrality of Sierpinski-type self-affine measures . J. Funct. Anal. 282(2022), 109310.CrossRefGoogle Scholar
Strichartz, R., Mock Fourier series and transforms associated with certain Cantor measures . J. Anal. Math. 81(2000), 209–238.CrossRefGoogle Scholar
Strichartz, R., Convergence of mock Fourier series . J. Anal. Math. 99(2006), 333–353.CrossRefGoogle Scholar
Wang, C. and Yin, F. L., Exponential orthonormal bases of Cantor–Moran measures . Fractals 27(2019), 1950136.CrossRefGoogle Scholar
Yan, Z. H., Spectral Moran measures on ${\mathbb{R}}^2$ . Nonlinearity 35(2022), 1261–1285.CrossRefGoogle Scholar