Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-05-02T15:57:15.748Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical coverings and X-raying convex bodies of constant width

Part of: General convexity Discrete geometry

Published online by Cambridge University Press:  13 December 2021

Andriy Bondarenko ,
Andriy Prymak Open the ORCID record for Andriy Prymak [Opens in a new window]  and
Danylo Radchenko
Andriy Bondarenko
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway e-mail: [email protected]
Andriy Prymak*
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, MB R3T 2N2, Canada
Danylo Radchenko
Affiliation:
Department of Mathematics, ETH Zurich, Zurich 8092, Switzerland e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

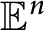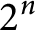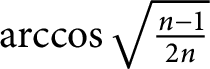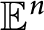Bezdek and Kiss showed that existence of origin-symmetric coverings of unit sphere in ${\mathbb {E}}^n$ by at most $2^n$ congruent spherical caps with radius not exceeding $\arccos \sqrt {\frac {n-1}{2n}}$ implies the X-ray conjecture and the illumination conjecture for convex bodies of constant width in ${\mathbb {E}}^n$ , and constructed such coverings for 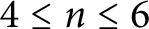$4\le n\le 6$ . Here, we give such constructions with fewer than 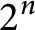$2^n$ caps for 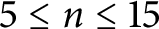$5\le n\le 15$ .

For the illumination number of any convex body of constant width in 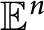${\mathbb {E}}^n$ , Schramm proved an upper estimate with exponential growth of order 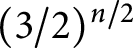$(3/2)^{n/2}$ . In particular, that estimate is less than 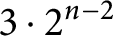$3\cdot 2^{n-2}$ for 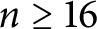$n\ge 16$ , confirming the abovementioned conjectures for the class of convex bodies of constant width. Thus, our result settles the outstanding cases 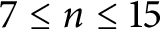$7\le n\le 15$ .

We also show how to calculate the covering radius of a given discrete point set on the sphere efficiently on a computer.

Keywords

Spherical covering radiusX-ray problemillumination problemconvex bodies of constant width

MSC classification

Primary: 52C17: Packing and covering in $n$ dimensions
Secondary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52A40: Inequalities and extremum problems 52C35: Arrangements of points, flats, hyperplanes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 860 - 866
Check for updates
Copyright
© Canadian Mathematical Society, 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was supported in part by Grant 275113 of the Research Council of Norway. The second author was supported by NSERC of Canada Discovery Grant RGPIN-2020-05357.

References

Bezdek, K. and Khan, M. A., The geometry of homothetic covering and illumination. In: Conder, M. D. E., Deza, A., and Weiss, A. I. (eds.), Discrete geometry and symmetry, Springer Proc. Math. Stat., 234, Springer, Cham, 2018, pp. 1–30.Google Scholar
Bezdek, K. and Kiss, Gy., On the X-ray number of almost smooth convex bodies and of convex bodies of constant width. Canad. Math. Bull. 52(2009), no. 3, 342–348.CrossRefGoogle Scholar
Bondarenko, A., Prymak, A., and Radchenko, D., Spherical coverings and X-raying convex bodies of constant width. Preprint, 2021. arXiv:2011.06398v2 CrossRefGoogle Scholar
Böröczky, K. Jr and Wintsche, G., Covering the sphere by equal spherical balls. In: Aronov, B., Basu, S., Pach, J., and Sharir, M. (eds.), Discrete and computational geometry, Algorithms Combin., 25, Springer, Berlin, 2003, pp. 235–251.CrossRefGoogle Scholar
Conway, J. H. and Sloane, N. J. A., Sphere packings, lattices and groups. 3rd ed., Grundlehren Math. Wiss. [Fundam. Principles Math. Sci.], 290, Springer, New York, 1999.CrossRefGoogle Scholar
Dai, F. and Prymak, A., On directional Whitney inequality. Canad. J. Math. (2021), 1–25. https://doi.org/10.4153/S0008414X21000110 Google Scholar
Danzer, L. and Grünbaum, B., Über zwei Probleme bezüglich konvexer Körper von P. Erdős und von V. L. Klee. Math. Z. 79(1962), 95–99 (in German). https://doi.org/10.1007/BF01193107 CrossRefGoogle Scholar
The Sage Developers, SageMath, the Sage Mathematics Software System (Version 9.2), 2020. https://www.sagemath.org Google Scholar
Dumer, I., Covering spheres with spheres. Discrete Comput. Geom. 38(2007), no. 4, 665–679.CrossRefGoogle Scholar
Huang, H., Slomka, B. A., Tkocz, T., and Vritsiou, B.-H., Improved bounds for Hadwiger’s covering problem via thin-shell estimates. J. Eur. Math. Soc. (2021). https://doi.org/10.4171/JEMS/1132 CrossRefGoogle Scholar
Martini, H., Montejano, L., and Oliveros, D., Bodies of constant width: an introduction to convex geometry with applications, Springer, Switzerland, 2019.CrossRefGoogle Scholar
Naszódi, M., On some covering problems in geometry. Proc. Amer. Math. Soc. 144(2016), no. 8, 3555–3562.CrossRefGoogle Scholar
Prymak, A. and Shepelska, V., On the Hadwiger covering problem in low dimensions. J. Geom. 111(2020), no. 3, 42.CrossRefGoogle Scholar
Rogers, C. A., A note on coverings. Mathematika 4(1957), 1–6.CrossRefGoogle Scholar
Rogers, C. A., Covering a sphere with spheres. Mathematika 10(1963), 157–164.CrossRefGoogle Scholar
Schramm, O., Illuminating sets of constant width. Mathematika 35(1988), no. 2, 180–189.CrossRefGoogle Scholar
Zong, C., A quantitative program for Hadwiger’s covering conjecture. Sci. China Math. 53(2010), no. 9, 2551–2560.CrossRefGoogle Scholar